Reader TTS

ABSTRACT Microlenses fabricated using flexible elastomers can be tuned in focal length by application of controlled strain. By varying the strain azimuthally, the lenses may be deformed

asymmetrically such that aberrations may be controlled. This approach is used to tune the astigmatism of the tunable lenses, and it is shown that the generated wavefront may be accurately

controlled. The lens presented here has an initial focal length of 32.6 mm and a tuning range of +2.3 mm for approximately 10% applied strain. The range of directly tunable Zernike

polynomials representing astigmatism is about 3 µm, while the secondary lens errors, which cannot be tuned directly, vary only by about 0.2 µm. SIMILAR CONTENT BEING VIEWED BY OTHERS

MONOLITHIC FOCUS-TUNABLE LENS TECHNOLOGY ENABLED BY DISK-TYPE DIELECTRIC-ELASTOMER ACTUATORS Article Open access 09 October 2020 STRAIN-TUNABLE OPTICAL MICROLENS ARRAYS WITH DEFORMABLE

WRINKLES FOR SPATIALLY COORDINATED IMAGE PROJECTION ON A SECURITY SUBSTRATE Article Open access 14 September 2022 STABILIZED DIRECTOR BUCKLING PATTERNS IN NEMATIC ELASTOMERS AND THEIR

DYNAMIC OPTICAL EFFECTS Article Open access 05 May 2022 INTRODUCTION A broad spectrum of tunable micro-optical components using a wide variety of physical effects has been proposed and

demonstrated.1 One approach with considerable potential is the mechanical deformation of microlenses entirely made of flexible elastomers: by controlled application of radial strain,

resulting in a change in lens curvature, it has been shown that the focal length can be tuned over a considerable range.2,3 To date, strain has only been applied symmetrically around these

tunable elastomeric lenses, such that only refractive power (focal length), but not other optical properties, have been tuned. A number of other tunable devices have considered the

astigmatism. For example, Beadie _et al._4 presented a tunable composite lens, one part being a fixed focal length lens made of poly(methylmetacrylate) and the tunable part using a membrane

with a poly(dimethylsiloxane) (PDMS) elastomer as a filling; the surface profiles showed an inherent astigmatism. Alternatively, singlet polymer lenses with thermal actuation have been

reported by Lee _et al._5 By choosing an anisotropic heater structure, Lee _et al._ were able to tune astigmatism along one axis, while the other axis remains fixed. A more versatile

approach with a combination of several membrane lenses was pursued by Marks _et al._6 Here two perpendicularly oriented cylindrical lenses provide variable astigmatism, whose total focus is

compensated with a rotational symmetric membrane lens. We show here that application of azimuthally varying strain to a deformable elastomer lens can result in controlled variation of

aberrations, particularly astigmatism. As a result, the microlens is not only tunable in focal length, but the concomitant aberrations can be increased or decreased at will. MATERIALS AND

METHODS LENS DESIGN AND CONCEPT The use of deformable elastomers for realizing strain-tunable lenses has been shown previously.3 Using the same approach, an equiconvex lens with identical

radii of curvature (=25.84 mm) was fabricated using a flexible, transparent elastomer (PDMS, SE 1740; Dow Corning Corp., Midland, MI, USA). In the unstrained, relaxed state, the resulting

lens yields a focal length of 32.6 mm for a refractive index of _n_PDMS=1.41,4 which corresponds to a numeric aperture of _NA_=0.24 (_f_#=2.0, free aperture, _a_0=16 mm, diameter, _d_=20 

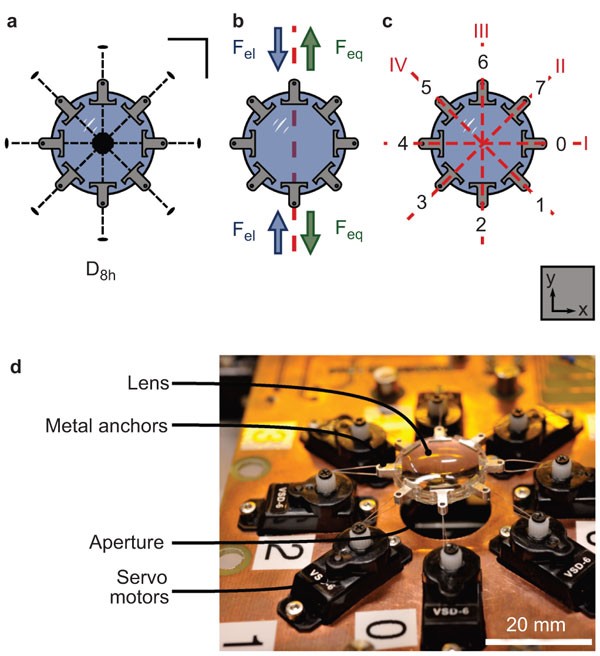
mm). As shown in Figure 1, eight mechanical anchors were embedded in opposing pairs at the periphery of the lens. Application of an outwardly oriented force in the plane of the lens then

results in strain-induced deformation. The Poisson’s ratio of PDMS rubbers is approximately 0.5,7 and due to conservation of the lens volume, the radius of curvature decreases for increasing

tensile strain and thus the focal length increases. This actuation concept is analogous to that of the mammalian eye, in which the ciliary muscle applies a radial force to the crystal lens

_via_ the zonular fibers.8 In contrast to the azimuthally symmetric actuation of the mammalian eye and also to membrane lenses, the latter actuated by pressure, the use of eight individual

actuators allows asymmetric deformation of the lens along four independent axes (a process to which we will refer as vectored actuation). Actuation along fewer than all axes will reduce the

overall symmetry of the lens and allows us to tune specific wavefront errors. As is usually done, we characterize the wavefront generated by the lens by Zernike polynomials, a set of

orthonormal functions.9 We focus here on the symmetry of the Zernike polynomials and the impact of vectored actuation on specific wavefront aberrations. While the actuation is asymmetric,

the pupil remains circular and Zernike polynomials can be applied to describe wavefront aberrations. We follow the definition given by Gross10 for the Zernike polynomials, namely, where _n_

denotes the radial order, _m_ denotes the azimuthal order and _ρ_ is the pupil radius over a unit pupil 0≤_ρ_≤1. We use the polar coordinate system in a strict mathematical sense, where _φ_

increases when rotating counterclockwise starting from the _x_-axis, which is also the system used by the wavefront sensor we employ below in the section on ‘Optical metrology’. This

wavefront description is useful since, if the actuation symmetry is congruent with the symmetry of a Zernike polynomial, only that particular wavefront aberration will be tuned. For example,

actuating axis _III_ tunes the Zernike polynomial AST0, as seen in Figure 2b. An additional important property of Zernike polynomials is the presence of nodal lines, which come in two

types: straight and circular. Straight nodal lines prevent crosstalk between actuation axes. The nodal lines correspond to neutral fibers in a mechanical model and enable the vectored

actuation of a tunable elastomeric lens to address specific wavefront aberrations independently from others as long as their symmetries match. Conversely, wavefront aberrations which

exclusively posses circular nodal lines will be influenced by all actuation axes in the same manner, as we will see in the section on ‘Results and discussion’. In summary, vectored actuation

will allow a controlled deformation of the elastomeric lens and thus a controlled change of the resulting wavefront. Pseudo-radially symmetric actuation (actuating all anchors at once) may

be used to influence radially symmetric wavefront aberrations such as defocus and spherical aberration and ‘asymmetric’ actuation can be used to control astigmatism. We will see how this is

achieved below. FABRICATION A reaction injection molding process is used to fabricate the biconvex elastomeric PDMS lenses. Figure 3 illustrates how the lens is produced by replica molding

using commercially available planoconcave glass lenses (Edmund Optics GmbH, Karlsruhe, Germany) as molds. These master lenses have a semidiameter of _d_=10 mm and radius of curvature of

=25.84 mm. Prior to first use, these glass lenses are coated with a thin (0.3–3 μm) layer of poly(p-xylylene) (parylene) to prevent adhesion of the PDMS during the molding process. The

parylene-coated lenses may be reused 5–10 times in further molding processes, before the parylene protection layer wears out. A poly(tetrafluorethylene) mount provides an intermediate spacer

layer and is also used to fix and align the eight pairwise diametrically opposed aluminum anchors. These anchors are fabricated by precision milling with dimensions of approximately 2×5×8 

mm3; the inner surface of the anchors facing the lens body has an area of 10 mm2. After sealing the mold, the PDMS precursor (SE1740) is injected with a syringe and subsequently cured in an

oven for 90 min at 90 °C. The mold is then allowed to slowly cool to room temperature and the elastomeric lens can then easily be demolded. The shrinking of the polymer during curing due to

thermal contraction is less than 1%, in agreement with Lee _et al._11 OPTICAL METROLOGY The wavefronts resulting from the lenses were measured at a wavelength of _λ_=633 nm using the

experimental set-up depicted in Figure 4. The light from the laser source passes a 1∶1 non-polarizing beam splitter and is then coupled into two single-mode fibers, which concomitantly

provide spatial filtering of the light source. After collimation, one arm of the system provides the reference wavefront (the lower part of Figure 4) and the second arm provides the

illumination for the lens under test. The light of the reference arm used to calibrate the wavefront sensor can be blocked by a shutter during the experiment. In the measurement arm (the

upper part of Figure 4), a microscope objective (M Plan Apo 10×, _f_=200 mm, _NA_=0.28; Mitutoyo, Kawasaki, Japan) is used to focus the measurement beam, yielding collimated output after the

lens under test. The objective is mounted on a motorized linear stage (M-531 with linear encoder; Physik Instrumente GmbH, Karlsruhe, Germany) to allow compensation for the change in

refractive power (focal length) of the tunable elastomeric lens by translating the microscope objective along the optical axis (vertical in Figure 4) during measurement. The tuning range of

the adaptive lens can be obtained directly by measuring the translation of the objective for zero defocus contribution to the wavefront overall error, as we will see in Figure 7. After

recombination of reference arm and test arm using a beam splitter, an afocal image relay optical system is used to project the exit pupil of the lens under test onto the entrance pupil of a

Shack-Hartmann wavefront sensor (WaveScope; Adaptive Optics Associates Inc., Cambridge, MA, USA). The image relay optics is a Keplerian telescope with an overall magnification of 1.25×

(_f_1=200 mm and _f_2=250 mm, both Fraunhofer doublets; Qioptiq Linos GmbH & Co. KG, Göttingen, Germany). The wavefront error was then determined by acquiring the first 36 Zernike

polynomials (the sixth order, both radial and azimuthal) from the Shack-Hartmann sensor. The zeroth order of the Zernike polynomials (piston) and the first order terms representing the lens

tilt (tilt _x_, tilt _y_) were ignored, while the defocus term was used to accurately position the microscope objective along the optical axis within an error in the defocus Zernike

coefficient (DEFOC in Figure 2) of _ε_=0.05 μm, approximately _λ_/12. Monitoring defocus served two functions: firstly, to keep the Shack-Hartmann sensor within the specified dynamic range

and hence prevent crosstalk between the subapertures; and secondly, to determine a measure of the focal length tuning range of the lens under test from the position of the stage holding the

microscope objective. RESULTS AND DISCUSSION ELASTOMERIC LENS IN THE RELAXED STATE Prior to any tuning experiments, we used the set-up described above to evaluate the quality of the

fabricated elastomer lenses in a comparative measurement with commercial fixed focal length glass lenses. Since neither curvature nor focal length of commercially available glass lenses can

be exactly matched with the PDMS lenses, we provide as close a comparison as possible by selecting lenses with similar curvatures and focal lengths and using the same aperture diameter (8 

mm). Figure 5 compares the measured wavefront errors for three different kinds of lenses: (i) the equiconvex elastomeric lens after demolding (_f_=32.6 mm, =25.84 mm); (ii) the elastomeric

lens in its relaxed, i.e., unactuated but mounted state; (iii) a fixed-focus, equiconvex singlet glass lens (LB1761, _f_=25.4 mm, =24.5 mm; Thorlabs Inc., Newton, NJ, USA); and (iv) a

fixed-focus glass achromatic doublet (G052009000, _f_=35 mm; Qioptiq Linos GmbH & Co. KG, Göttingen, Germany). The singlet glass reference lens was chosen to provide a reference with a

similar radius of curvature as that of the symmetric biconvex elastomeric lens (=24.5 mm _vs._ =24.8 mm). Both lenses are of comparable thickness and no observable sagging of the elastomeric

lens occurred during measurement. The achromatic lens was selected as an aberration-corrected reference, since achromatic lenses are by definition corrected for longitudinal chromatic

aberration as well as for spherical aberration. All measurements were conducted with an aperture diameter of 8 mm. From Figure 5, it can be clearly seen that the overall wavefront

aberrations of the unactuated elastomeric lens are comparable to those of the commercial singlet glass lens. Both suffer—as expected for spherical singlet lenses—from spherical aberration

(SPHA) and show almost equal amounts of astigmatism (AST0 and AST45). Figure 5 also shows the higher-order Zernike coefficients representing the tetrafoil wavefront aberration, whose

symmetry corresponds to that of the buried anchors. The value of this aberration in the demolded elastomeric lens is also similar to that present in the reference singlet glass lens (cf.

Figure 5a and 5c). Comparing the relaxed and mounted elastomeric lenses in Figure 5a and 5b, one can see that the TF1 error is increased when the lens is mounted (Figure 5b); this increase

indicates that the lens is slightly pre-stressed and originates from the calibration procedure described below in the section on ‘Actuator calibration’. We see from these results that

reaction injection molding is a suitable manufacturing process for solid elastomeric lenses, as neither the fabrication process nor embedding the anchors introduces significant wavefront

errors. TUNED ELASTOMERIC LENS ACTUATOR CALIBRATION Vectored actuation relies on strain applied radially to the lens using the eight embedded anchors. Strain is applied to these anchors

using eight motors as actuators, as seen in Figure 1b. Before measurement, these actuators were calibrated and aligned laterally such that the optical axis of the lens coincides with the

optical axis of the illumination beam. Subsequently, the motors were actuated consecutively while observing the coefficient for the DEFOC wavefront aberration. The initial state of the lens

was then defined to be at the point at which the coefficient began to change when actuating a single motor. TUNABLE ASTIGMATISM We first discuss the influence of the applied strain on the

Zernike polynomials for astigmatism (AST0 and AST45) when actuating with congruent symmetry. Figure 6 shows measurement results for actuating the elastomeric lens along the axes _I_ and

_III_ corresponding to the _x_ and _y_ axes in a Cartesian coordinate system. Deforming the lens along its _x_-axis results in an increasing Zernike coefficient for AST0 (Figure 6a), while

straining the lens parallel to its _y_-axis causes the same coefficient to decrease (Figure 6b). The absolute values of this change in the AST0 coefficient are approximately the same, as

summarized in Table 1; in this table, ‘slope’ refers to the change in the Zernike coefficient (in micrometers) for unit strain defined as the ratio of the elongation Δ_a_ to the initial free

aperture _a_0. This theoretical prediction of subsection: Lens design and concept is clearly confirmed by the experimental data in Figure 6a and 6b: the AST0 coefficient evolves linearly

with the applied strain, its sign depending on the axis on which the strain is applied. If, in contrast, two orthogonal axes are actuated simultaneously, the effect of one axis on the AST0

polynomial is canceled out by the other. Straining the lens on both orthogonal axes simultaneously will therefore result in a negligible change in astigmatism for _x_–_y_ direction (AST0) as

can be seen in Figure 6c and Table 1. The experimental results shown in Figure 6c distinctly support the prediction of subsection: Lens design and concept that straining two orthogonally

oriented axes (in the Zernike sense) will _not_ tune the Zernike polynomial corresponding to that symmetry. It was also shown in Figure 6 that the AST0 astigmatism can be tuned independently

from AST45 astigmatism as expected from the location of the nodal lines and the congruence of the symmetry of the wavefront aberration and actuation symmetry. Although Zernike polynomials

have been conceived to be orthonormal, axes _II_ and _IV_ are not so with respect to the main axes, _I_ and _III_, in the reference coordinate system. Actuating the elastomeric lens along

axis _I_, however, will only tune the wavefront error represented by the Zernike polynomial AST0, but will leave the coefficient AST45 unchanged, as can be seen in Figure 6d. The same holds

true for actuation along any other axis of the presented lens, or for simultaneous actuation of the two perpendicular axes _I_ and _III_ in Cartesian space: the AST45 coefficient does not

change. This characteristic results from the elastic properties of the lens, since the axes themselves are not linearly independent. The absence of crosstalk between actuation axes can also

be observed for wavefront aberrations with higher azimuthal frequency like TF1 and TF2 in Table 1, and emphasizes the unique properties of the solid body elastomeric lens. FOCAL LENGTH

TUNING The unstrained focal length of the elastomeric lens was determined to be 32.2±0.8 mm, which fits well to the theoretical value of 32.6 mm calculated from lens curvature and refractive

index, providing the unstrained value for focal length in Figure 7. The focal length was then tuned by applying vectored strain to the elastomeric lens along four different axes _I_–_IV_.

The expected linear relationship between the applied strain and the focal length of the lens is shown in Figure 7 and Table 2. We find an overall tuning range of 2.4 mm corresponding to

Δ_f_rel=Δ_f_/_f_0≈7% for joint actuation of all axes of the lens. Actuating a single axis will reduce the tuning range to approximately one fourth of that value (0.6 mm), which also reveals

that straining the lens along all four axes simultaneously does not exceed the linear regime of the polymer elasticity: when we superpose the focal length tuning length of each individual

axis (gray dashed line), we find only a negligible deviation from all-symmetric actuation (red circles in Figure 7). Any deviation from linear strain behavior of the lens would have

manifested itself in non-overlapping curves. It should be mentioned that the polymer was strained under quasi-static conditions; no viscous contributions had to be considered and, since the

polymer is strictly crosslinked (a gel), no creep occurs. As a result, the polymer lens exhibits a focus stable with time. The responsiveness of the lens tuning depends primarily on the

speed of the actuators. The time to get to a set focal length takes a few seconds which is due to the control loop of the actuators. No birefringence was observed inside the free aperture

while straining the elastomeric lens. Some weak strain-induced birefringence was noticed close to the embedded anchors, but due to the high flexibility of the siloxane, the birefringence

does not encroach on the free aperture. Straining the lens thus has no negative effect on its optical performance. DISCUSSION The tunability of the primary lens aberrations, predominantly

astigmatism, is summarized for various actuation configurations in Table 1 and Figure 6. From these characteristics, we see that the tetrafoil error (TF1) is almost not affected if all axes,

_I_–_IV_, are actuated at once, because—as was shown in Figure 6 for AST0—the effects cancel if orthogonal axes are actuated simultaneously. As the behavior of the TF1 wavefront aberration

shows, the actuation axes do not necessarily have to be perpendicular as it was the case for the AST0 and AST45 pair; the actuation symmetry must just be congruent with the symmetry of the

desired wavefront aberration. We note that not all wavefront aberrations can be arbitrarily tuned. For example, for all-axes actuation, the slope for the SPHA will be four times as large as

that shown in Table 1 for single axis actuation alone. However, SPHA will always be tuned by actuation along _any_ axis due to its completely rotational symmetry. Actuating all axes at once

will also lead to an increase of wavefront aberrations with eightfold azimuthal frequency, which unfortunately cannot be resolved by the employed wavefront sensor. Finally, we see that the

tuning magnitude of a specific aberration exceeds that of the non-actuated and orthonormal aberrations by factors of between 20 and 100. Aberrations such as coma are easily introduced by

lens tilt and cannot be completely avoided in the set-up used. Even though the magnitude of coma, for example, is larger than that of astigmatism, its variation due to actuation is almost a

factor of 100 (COMA X) or 35 (COMA Y) smaller than that of the directly tuned AST0 and AST45, comparable to the almost negligible crosstalk between AST0 and AST45, which arises when

non-congruent axes are used for actuation. CONCLUSION We have shown that an elastomeric lens can be deformed by vectored actuation to selectively tune specific wavefront aberrations in

addition to allowing focal length tuning over a significant range. Elastomeric lenses thus differ significantly from pressure-actuated membrane lenses, since the latter will need at least

three membranes to tune, for example, focal length and astigmatism.6 Furthermore, elastomeric lenses benefit from a well-defined optical surface even in the unstrained state, in contrast to

liquid lenses, where the surface is shaped by an equilibrium of surface tension and gravity, and membrane-type lenses, where the membrane must be significantly distended to achieve short

focal lengths. Finally, gravitational sagging (introducing coma as a dominant wavefront error), which is an issue for many membrane lenses, does not occur with these bulk elastomeric lenses.

Many of the advantages of the tunable elastomeric lenses mentioned above suggest their applicability to a range of applications. The well-defined optical surface in the non-actuated state,

for example, implies that they may be used in autofocus systems; the tuning range required to achieve focus in camera systems is small and that range is easily accomplished with solid

elastomeric lenses. Alternatively, vectored actuation and the manipulation of astigmatism could be directly applied to laser beam shaping, for example, to compensate for thermal drift in the

laser cavity which results in a non-uniform irradiation distribution. Furthermore, in ophthalmology, tunable elastomeric lenses lend themselves to the realization of an adaptive phoropter

for characterization of astigmatism in the patient’s vision; a single elastomeric lens could perform this function, whereas fluidic- or membrane-based lenses would require a stack of three

individual lenses. Finally, since the form of the relaxed lens is defined by the mold and can be chosen arbitrarily, a combination of two lenses with tunable astigmatism could be applied to

adaptive anamorphic imaging, using elastomeric lenses with a strong cylindric preference in one axis. These examples illustrate only a few of the possible applications of these lenses in

adaptive optics. REFERENCES * Friese C, Werber A, Krogmann F, Mönch W, Zappe H . Materials, effects and components for tunable micro-optics. _IEEJ Trans Electr Electron Eng_ 2007; 2:

232–248. Article  Google Scholar  * Santiago-Alvarado A, Vázquez-Montiel S, Granados-Agustín FS, González-García J, Rueda-Soriano E _et al_. Measurement of aberrations of a solid elastic

lens using a point-diffraction interferometer. _Opt Eng_ 2010; 49: 123401. Article  ADS  Google Scholar  * Liebetraut P, Petsch S, Mönch W, Zappe H . Tunable solid-body elastomer lenses with

electromagnetic actuation. _Appl Opt_ 2011; 50: 3268. Article  ADS  Google Scholar  * Beadie G, Sandrock ML, Wiggins MJ, Lepkowicz RS, Shirk JS _et al_. Tunable polymer lens. _Opt Express_

2008; 16: 11847–11857. Article  ADS  Google Scholar  * Lee SY, Chen WC, Tung HW, Fang W . Microlens with tunable astigmatism. _IEEE Photon Technol Lett_ 2007; 19: 1383–1385. Article  ADS 

Google Scholar  * Marks R, Mathine DL, Peyman G, Schwiegerling J, Peyghambarian N . Adjustable adaptive compact fluidic phoropter with no mechanical translation of lenses. _Opt Lett_ 2010;

35: 739–741. Article  ADS  Google Scholar  * Kuo AC . _Polymer Data Handbook. 1st ed_. Oxford: Oxford University Press; 1999. pp411–435. Google Scholar  * Atchison DA, Smith G . _Optics of

the Human Eye_. Oxford: Butterworth Heinemann; 2006. Google Scholar  * Lakshminarayanan V, Fleck A . Zernike polynomials: a guide. _J Mod Opt_ 2011; 58: 545–561. Article  ADS  Google Scholar

  * Gross H . _Fundamentals of Technical Optics. Vol. 1_. Weinheim: Wiley-VCH; 2005. Google Scholar  * Lee SW, Lee SS . Shrinkage ratio of PDMS and its alignment method for the wafer level

process. _Microsyst Technol_ 2007; 14: 205–208. Article  Google Scholar  Download references ACKNOWLEDGEMENTS This work was funded by the German Science Foundation within the framework of

the Priority Program 1337 Aktive Mikrooptik. The authors thank Philipp Müller and the Laboratory for Biomedical Technology at IMTEK for coating the master lenses. AUTHOR INFORMATION AUTHORS

AND AFFILIATIONS * Department of Microsystems Engineering, Gisela and Erwin Sick Chair of Micro-optics, University of Freiburg, Freiburg 79110, Germany Peter Liebetraut, Sebastian Petsch, 

Jens Liebeskind & Hans Zappe Authors * Peter Liebetraut View author publications You can also search for this author inPubMed Google Scholar * Sebastian Petsch View author publications

You can also search for this author inPubMed Google Scholar * Jens Liebeskind View author publications You can also search for this author inPubMed Google Scholar * Hans Zappe View author

publications You can also search for this author inPubMed Google Scholar CORRESPONDING AUTHOR Correspondence to Hans Zappe. RIGHTS AND PERMISSIONS This work is licensed under the Creative

Commons Attribution-NonCommercial-No Derivative Works 3.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-nd/3.0/ Reprints and permissions

ABOUT THIS ARTICLE CITE THIS ARTICLE Liebetraut, P., Petsch, S., Liebeskind, J. _et al._ Elastomeric lenses with tunable astigmatism. _Light Sci Appl_ 2, e98 (2013).

https://doi.org/10.1038/lsa.2013.54 Download citation * Received: 06 February 2013 * Revised: 28 May 2013 * Accepted: 03 June 2013 * Published: 13 September 2013 * Issue Date: September 2013

* DOI: https://doi.org/10.1038/lsa.2013.54 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative KEYWORDS * aberrations * active or adaptive optics * micro-optical

devices * polymers