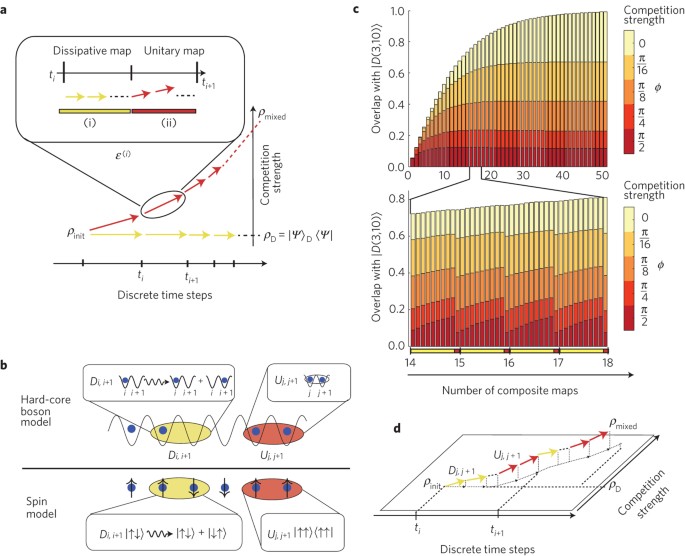
Quantum simulation of dynamical maps with trapped ions
- Select a language for the TTS:
- UK English Female
- UK English Male
- US English Female
- US English Male
- Australian Female
- Australian Male
- Language selected: (auto detect) - EN
Play all audios:

ABSTRACT Dynamical maps describe general transformations of the state of a physical system—their iteration interpreted as generating a discrete time evolution. Prime examples include
classical nonlinear systems undergoing transitions to chaos. Quantum mechanical counterparts show intriguing phenomena such as dynamical localization on the single-particle level. Here we
extend the concept of dynamical maps to a many-particle context, where the time evolution involves both coherent and dissipative elements: we experimentally explore the stroboscopic dynamics
of a complex many-body spin model with a universal trapped ion quantum simulator. We generate long-range phase coherence of spin by an iteration of purely dissipative quantum maps and
demonstrate the characteristics of competition between combined coherent and dissipative non-equilibrium evolution—the hallmark of a previously unobserved dynamical phase transition. We
assess the influence of experimental errors in the quantum simulation and tackle this problem by developing an efficient error detection and reduction toolbox based on quantum feedback.
Access through your institution Buy or subscribe This is a preview of subscription content, access via your institution ACCESS OPTIONS Access through your institution Subscribe to this
journal Receive 12 print issues and online access $259.00 per year only $21.58 per issue Learn more Buy this article * Purchase on SpringerLink * Instant access to full article PDF Buy now
Prices may be subject to local taxes which are calculated during checkout ADDITIONAL ACCESS OPTIONS: * Log in * Learn about institutional subscriptions * Read our FAQs * Contact customer
support SIMILAR CONTENT BEING VIEWED BY OTHERS QUANTUM SIMULATION OF SPIN-BOSON MODELS WITH STRUCTURED BATH Article Open access 30 April 2025 UNCOVERING LOCAL INTEGRABILITY IN QUANTUM
MANY-BODY DYNAMICS Article Open access 15 March 2025 OBSERVATION OF A FINITE-ENERGY PHASE TRANSITION IN A ONE-DIMENSIONAL QUANTUM SIMULATOR Article 17 January 2025 REFERENCES * Maze, J. R.
et al. Nanoscale magnetic sensing with an individual electronic spin in diamond. _Nature_ 455, 644–647 (2008). Article ADS Google Scholar * Ladd, T. D. et al. Quantum computers. _Nature_
464, 45–53 (2010). Article ADS Google Scholar * Wrachtrup, J. & Jelezko, F. Processing quantum information in diamond. _J. Phys. Condens. Matter_ 18, 807–824 (2006). Article ADS
Google Scholar * Clarke, J. & Wilhelm, F. K. Superconducting quantum bits. _Nature_ 453, 1031–1042 (2008). Article ADS Google Scholar * O’Brien, J. L. Optical quantum computing.
_Science_ 318, 1567–1570 (2007). Article ADS Google Scholar * Hanson, R., Kouwenhoven, L. P., Petta, J. R., Tarucha, S. & Vandersypen, L. M. K. Spins in few-electron quantum dots.
_Rev. Mod. Phys._ 79, 1217–1265 (2007). Article ADS Google Scholar * Schneider, C., Porras, D. & Schätz, T. Experimental quantum simulations of many-body physics with trapped ions.
_Rep. Prog. Phys._ 75 024401 (2012). * Saffman, M., Walker, T. G. & Mølmer, K. Quantum information with Rydberg atoms. _Rev. Mod. Phys._ 82, 2313–2363 (2010). Article ADS Google
Scholar * Bloch, I., Dalibard, J. & Nascimbène, S. Quantum simulations with ultracold quantum gases. _Nature Phys._ 8, 267–276 (2012). Article ADS Google Scholar * Blatt, R. &
Roos, C. F. Quantum simulations with trapped ions. _Nature Phys._ 8, 277–284 (2012). Article ADS Google Scholar * Aspuru-Guzik, A. & Walther, P. Photonic quantum simulators. _Nature
Phys._ 8, 285–291 (2012). Article ADS Google Scholar * Houck, A. A., Türeci, H. E. & Koch, J. On-chip quantum simulation with superconducting circuits. _Nature Phys._ 8, 292–299
(2012). Article ADS Google Scholar * Bacon, D. et al. Universal simulation of Markovian quantum dynamics. _Phys. Rev. A_ 64, 062302 (2001). Article ADS Google Scholar * Lloyd, S. &
Viola, L. Engineering quantum dynamics. _Phys. Rev. A_ 65, 010101 (2001). Article MathSciNet Google Scholar * Lidar, D. A., Chuang, I. L. & Whaley, K. B. Decoherence-free subspaces
for quantum computation. _Phys. Rev. Lett._ 81, 2594–2597 (1998). Article ADS Google Scholar * Baggio, G., Ticozzi, F. & Viola, L. in _2012 IEEE 51st Annual Conference on Decision and
Control (CDC)_ 1072–1077 (IEEE, 2012). * Nielsen, M. A. & Chuang, I. L. _Quantum Computation and Quantum Information_ (Cambridge Univ. Press, 2000). MATH Google Scholar * Lloyd, S.
Universal quantum simulators. _Science_ 273, 1073–1078 (1996). Article ADS MathSciNet Google Scholar * Lanyon, B. P. et al. Universal digital quantum simulation with trapped ions.
_Science_ 334, 57–61 (2011). Article ADS Google Scholar * Zhang, J., Yung, M-H., Laflamme, R., Aspuru-Guzik, A. & Baugh, J. Digital quantum simulation of the statistical mechanics of
a frustrated magnet. _Nature Commun._ 3, 880 (2012). Article ADS Google Scholar * Poyatos, J. F., Cirac, J. I. & Zoller, P. Quantum reservoir engineering with laser cooled trapped
ions. _Phys. Rev. Lett._ 77, 4728–4731 (1996). Article ADS Google Scholar * Cho, J., Bose, S. & Kim, M. S. Optical pumping into many-body entanglement. _Phys. Rev. Lett._ 106, 020504
(2011). Article ADS Google Scholar * Kastoryano, M. J., Reiter, F. & Sørensen, A. S. Dissipative preparation of entanglement in optical cavities. _Phys. Rev. Lett._ 106, 090502
(2011). Article ADS Google Scholar * Krauter, H. et al. Entanglement generated by dissipation and steady state entanglement of two macroscopic objects. _Phys. Rev. Lett._ 107, 080503
(2011). Article ADS Google Scholar * Barreiro, J. T. et al. An open-system quantum simulator with trapped ions. _Nature_ 470, 486–491 (2011). Article ADS Google Scholar * Verstraete,
F., Wolf, M. M. & Cirac, J. I. Quantum computation and quantum-state engineering driven by dissipation. _Nature Phys._ 5, 633–636 (2009). Article ADS Google Scholar * Pastawski, F.,
Clemente, L. & Cirac, J. I. Quantum memories based on engineered dissipation. _Phys. Rev. A_ 83, 012304 (2011). Article ADS Google Scholar * Kliesch, M., Barthel, T., Gogolin, C.,
Kastoryano, M. & Eisert, J. Dissipative quantum Church-Turing theorem. _Phys. Rev. Lett._ 107, 120501 (2011). Article ADS Google Scholar * Diehl, S. et al. Quantum states and phases
in driven open quantum systems with cold atoms. _Nature Phys._ 4, 878–883 (2008). Article ADS Google Scholar * Weimer, H., Müller, M., Lesanovsky, I., Zoller, P. & Büchler, H. P. A
Rydberg quantum simulator. _Nature Phys._ 6, 382–388 (2010). Article ADS Google Scholar * Diehl, S., Rico, E., Baranov, M. A. & Zoller, P. Topology by dissipation in atomic quantum
wires. _Nature Phys._ 7, 971–977 (2011). Article ADS Google Scholar * Gardiner, C. W. & Zoller, P. _Quantum Noise_ (Springer, 1999). MATH Google Scholar * Reichl, L. E. _The
Transition to Chaos In Conservative Classical Systems: Quantum Manifestations_ (Springer, 1992). Book Google Scholar * Chirikov, B. V. A universal instability of many-dimensional
oscillator systems. _Phys. Rep._ 52, 263–379 (1979). Article ADS MathSciNet Google Scholar * Izrailev, F. M. Simple models of quantum chaos: spectrum and eigenfunctions. _Phys. Rep._
196, 299–392 (1990). Article ADS MathSciNet Google Scholar * Haake, F. _Quantum Signatures of Chaos_ (Synergetics Series, Springer, 2010). Book Google Scholar * Moore, F. L., Robinson,
J. C., Bharucha, C. F., Sundaram, B. & Raizen, M. G. Atom optics realization of the quantum delta-kicked rotor. _Phys. Rev. Lett._ 75, 4598–4601 (1995). Article ADS Google Scholar *
Ammann, H., Gray, R., Shvarchuck, I. & Christensen, N. Quantum delta-kicked rotor: Experimental observation of decoherence. _Phys. Rev. Lett._ 80, 4111–4115 (1998). Article ADS Google
Scholar * d’Arcy, M. B., Godun, R. M., Oberthaler, M. K., Cassettari, D. & Summy, G. S. Quantum enhancement of momentum diffusion in the delta-kicked rotor. _Phys. Rev. Lett._ 87,
074102 (2001). Article ADS Google Scholar * Henderson, K., Kelkar, H., Li, T. C., Gutierrez-Medina, G. & Raizen, M. G. Bose–Einstein condensate driven by a kicked rotor in a finite
box. _Europhys. Lett._ 75, 392 (2006). Article ADS Google Scholar * Porras, D. & Cirac, J. I. Effective quantum spin systems with trapped ions. _Phys. Rev. Lett._ 92, 207901 (2004).
Article ADS Google Scholar * Friedenauer, A., Schmitz, H., Glueckert, J. T., Porras, D. & Schaetz, T. Simulating a quantum magnet with trapped ions. _Nature Phys._ 4, 757–761 (2008).
Article ADS Google Scholar * Kim, K. et al. Quantum simulation of frustrated Ising spins with trapped ions. _Nature_ 465, 590–593 (2010). Article ADS Google Scholar * Islam, R. et al.
Onset of a quantum phase transition with a trapped ion quantum simulator. _Nature Commun._ 2, 377 (2011). Article ADS Google Scholar * Britton, J. W. et al. Engineered two-dimensional
Ising interactions in a trapped-ion quantum simulator with hundreds of spins. _Nature_ 484, 489–492 (2012). Article ADS Google Scholar * Diehl, S., Tomadin, A., Micheli, A., Fazio, R.
& Zoller, P. Dynamical phase transitions and instabilities in open atomic many-body systems. _Phys. Rev. Lett._ 105, 015702 (2010). Article ADS Google Scholar * Sachdev, S. _Quantum
Phase Transitions_ (Cambridge Univ. Press, 1999). MATH Google Scholar * Mølmer, K. & Sørensen, A. Multiparticle entanglement of hot trapped ions. _Phys. Rev. Lett._ 82, 1835–1838
(1999). Article ADS Google Scholar * Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. _Nature_ 417, 709–711 (2002). Article ADS
Google Scholar * Sayrin, C. et al. Real-time quantum feedback prepares and stabilizes photon number states. _Nature_ 477, 73–77 (2011). Article ADS Google Scholar Download references
ACKNOWLEDGEMENTS We gratefully acknowledge support by the Austrian Science Fund (FWF), through the SFB FoQus (FWF Project No. F4002-N16 and F4016-N16) and the START grant Y 581-N16 (S.D.),
by the European Commission (AQUTE), as well as the Institut für Quantenoptik und Quanteninformation GmbH. This research was funded by the Office of the Director of National Intelligence
(ODNI), Intelligence Advanced Research Projects Activity (IARPA), through the Army Research Office grant W911NF-10-1-0284. All statements of fact, opinion or conclusions contained herein are
those of the authors and should not be construed as representing the official views or policies of IARPA, the ODNI or the US Government. M.M. acknowledges support by the CAM research
consortium QUITEMAD S2009-ESP-1594, European Commission PICC: FP7 2007-2013, Grant No. 249958, and the Spanish MICINN grant FIS2009-10061. AUTHOR INFORMATION Author notes * J. T. Barreiro
Present address: Present address: Fakultät für Physik, Ludwig-Maximilians-Universität München and Max-Planck Institute of Quantum Optics, Germany, * P. Schindler and M. Müller: These authors
contributed equally to this work AUTHORS AND AFFILIATIONS * Institut für Experimentalphysik, Universität Innsbruck, Technikerstrasse 25, 6020 Innsbruck, Austria P. Schindler, D. Nigg, J. T.
Barreiro, E. A. Martinez, M. Hennrich, T. Monz & R. Blatt * Departamento de Física Teórica I, Universidad Complutense, Avenida Complutense s/n, 28040 Madrid, Spain M. Müller * Institut
für Theoretische Physik, Universität Innsbruck, Technikerstrasse 25, 6020 Innsbruck, Austria S. Diehl & P. Zoller * Institut für Quantenoptik und Quanteninformation, Österreichische
Akademie der Wissenschaften, Technikerstrasse 21A, 6020 Innsbruck, Austria S. Diehl, P. Zoller & R. Blatt Authors * P. Schindler View author publications You can also search for this
author inPubMed Google Scholar * M. Müller View author publications You can also search for this author inPubMed Google Scholar * D. Nigg View author publications You can also search for
this author inPubMed Google Scholar * J. T. Barreiro View author publications You can also search for this author inPubMed Google Scholar * E. A. Martinez View author publications You can
also search for this author inPubMed Google Scholar * M. Hennrich View author publications You can also search for this author inPubMed Google Scholar * T. Monz View author publications You
can also search for this author inPubMed Google Scholar * S. Diehl View author publications You can also search for this author inPubMed Google Scholar * P. Zoller View author publications
You can also search for this author inPubMed Google Scholar * R. Blatt View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS M.M., P.S., J.T.B.
and S.D. developed the research, based on theoretical ideas conceived with P.Z.; P.S. and D.N. performed the experiments; P.S. and T.M. analysed the data; P.S., J.T.B., D.N., T.M., E.A.M.,
M.H. and R.B. contributed to the experimental set-up; P.S., M.M. and S.D wrote the manuscript, with revisions provided by J.T.B., P.Z. and R.B; all authors contributed to the discussion of
the results and manuscript. CORRESPONDING AUTHORS Correspondence to P. Zoller or R. Blatt. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests.
SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION Supplementary Information (PDF 1937 kb) RIGHTS AND PERMISSIONS Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Schindler,
P., Müller, M., Nigg, D. _et al._ Quantum simulation of dynamical maps with trapped ions. _Nature Phys_ 9, 361–367 (2013). https://doi.org/10.1038/nphys2630 Download citation * Received: 07
December 2012 * Accepted: 15 April 2013 * Published: 19 May 2013 * Issue Date: June 2013 * DOI: https://doi.org/10.1038/nphys2630 SHARE THIS ARTICLE Anyone you share the following link with
will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt
content-sharing initiative
