Reader TTS

ABSTRACT Optical interference is not only a fundamental phenomenon that has enabled new theories of light to be derived but it has also been used in interferometry for the measurement of

small displacements, refractive index changes, and surface irregularities. In a two-beam interferometer, variations in the interference fringes are used as a diagnostic for anything that

causes the optical path difference (OPD) to change; therefore, for a specified OPD, greater variation in the fringes indicates better measurement sensitivity. Here, we introduce and

experimentally validate an interesting optical interference phenomenon that uses photons with a structured frequency-angular spectrum, which are generated from a spontaneous parametric

down-conversion process in a nonlinear crystal. This interference phenomenon is manifested as interference fringes that vary much more rapidly with increasing OPD than the corresponding

fringes for equal-inclination interference; the phenomenon is parameterised using an equivalent wavelength, which under our experimental conditions is 29.38 nm or about 1/27 of the real

wavelength. This phenomenon not only enriches the knowledge with regard to optical interference but also offers promise for applications in interferometry. SIMILAR CONTENT BEING VIEWED BY

OTHERS MONOCHROMATIC LIGHT MEASUREMENT VIA GEOMETRIC PHASE AND FOURIER-TRANSFORM SPECTROSCOPY METHOD Article Open access 28 July 2022 INTENSITY-BASED HOLOGRAPHIC IMAGING VIA SPACE-DOMAIN

KRAMERS–KRONIG RELATIONS Article 08 February 2021 3D STOCHASTIC INTERFEROMETER DETECTS PICOMETER DEFORMATIONS AND MINUTE DIELECTRIC FLUCTUATIONS OF ITS OPTICAL VOLUME Article Open access 26

September 2022 INTRODUCTION Since the observation of double–slit interference by Young in 1807, optical interference phenomena have provided multiple demonstrations of the wave nature of

light. After that pioneering experiment, many studies on interferences have been performed to reveal the deeper nature of light, for example, the wave–particle duality of photons1,2,3 and

their high-order correlations4,5. To date, interference phenomena have been observed not only in the light intensity, but also in other degrees of freedom of light6, including the

frequency7, polarisation8, and orbital angular momentum9, and have thus played an important role in various structured light generation applications10. Fringe patterns are a common feature

of most interference phenomena and these fringes form the basis of interferometers, which have proven to be powerful practical tools in numerous fields, e.g., in gravitational-wave

detection11, optical coherence tomography12, Fourier transform infrared spectroscopy13, and applications of fibre optic gyroscopes14. For light intensity interference, the existence of

constructive and destructive interference is dependent on a stable phase difference between two or more light beams. In traditional interferometers, the stable phase difference is determined

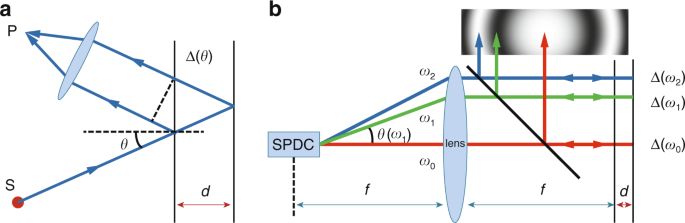
by the optical path difference (OPD). For example, in equal–inclination interference15 (Fig. 1a), the OPD between the two reflecting surfaces changes with incident angle, and therefore,

light with the same incident angle finally superposes to form a bright or dark fringe. Features of the interference fringe patterns are also dependent on the properties of the light source.

Most past studies and applications of interference have used lasers or thermal light sources. In recent years, a new light source based on spontaneous parametric down-conversion (SPDC)16,17

in nonlinear crystals has been attracting much attention. The SPDC is a second-order nonlinear process, in which a higher-energy pump photon splits into a pair of lower-energy photons, one

designated a signal photon and the other an idler photon, emerging with a certain probability from a nonlinear crystal. This special source of light has helped in finding many novel

interference phenomena4,18,19,20 and applications21,22,23,24,25,26,27,28,29,30 that are quite different from those using lasers or thermal light sources31,32,33. If the entanglement

properties are ignored, each arm (subsystem) of an SPDC source can usually be regarded as an incoherent mix of photons with all possible spatial modes and frequencies. Unlike lasers or

thermal light sources, in which the spatial modes and frequency components can be treated independently, photons from an SPDC source have a structured frequency-angular spectrum (FAS) caused

by the phase-matching conditions. The emission angles outside the nonlinear crystal are dependent on the emitted photon frequencies. For a long crystal, this dependence relation is

approximately a one-to-one mapping that is governed by a tuning curve31, which can be approximated as a parabola. In this work, we have observed a distinctive two-beam interference

phenomenon in an amplitude division interferometer using photons from one arm of an SPDC source (Fig. 1b); we refer to it as angular-spectrum-dependent (ASD) interference because it is

caused by a combination of interference patterns of different angular components. The principle and phenomenon of the ASD interference are very similar to those of the traditional

equal-inclination interference: they both have ring-like fringes, the phase difference inducing bright or dark rings is dependent on the angle, and the number of rings is dependent on the

distance _d_. However, ASD interference is fundamentally different from traditional equal-inclination interference. The creation and properties of ASD interference are closely related to the

frequency-angular one-to-one mapping relation of the SPDC process. To illustrate the properties of ASD interference (Fig. 1b) and distinguish it from the traditional equal-inclination

interference (Fig. 1a), we compare them in terms of the following five aspects. First, the two light sources have different radiation properties: the point source shown in Fig. 1a radiates

spherical waves that are isotropic, but the SPDC process shown in Fig. 1b radiates photons over a very wide spectrum, where the photon frequencies are related to the emission angle _θ_(_ω_),

which is shown using Eq. (1). Second, with regard to their principles of interference, the phase differences _nπ_ for the bright or dark fringes are caused by the angular-dependent OPDs

Δ(_θ_) of the light in Fig. 1a, whereas the phase differences _nπ_ are caused by the specific photon frequencies _ω__n_ in Fig. 1b. Third, in Fig. 1a, the photons in each of the fringes are

coherent and have the same spectrum and the interference visibility is thus dependent on the width of the spectrum; in Fig. 1b, however, the photons in the different fringes have different

frequencies and the fringe visibility is dependent on the width of the FAS. Fourth, in the optical setups, the lens in Fig. 1a allows observation of the far-field of the fringes that are

created, while the lens shown in Fig. 1b is used for collimation. Finally, the interference patterns of the two phenomena are both ring-like fringes, but with increasing distance _d_ between

the two reflecting surfaces, the fringes of the ASD interference vary much more quickly than those in the traditional interference pattern; in other words, much shorter distance _d_ are

required for the ASD interference to obtain the same interference patterns. In stressing this last point, we say that the equivalent wavelength of this ASD interference is much shorter than

the actual wavelength. The physical meaning of the equivalent wavelength here is that the ASD interference fringes are the same as those from a traditional equal-inclination interferometer

in which the wavelength of the photons has this value. In the following, the equivalent wavelength is defined so that the expression for the phase difference has the same form as that for

the traditional interference. The FAS of the SPDC has been reported previously31,34. Shih calculated the tuning curve required for type-I and type-II angle phase-matching31. Burlakov et

al.34 calculated the intensity distribution of the FAS near the degenerate phase-matching condition and presented a photograph of this distribution; they implemented the second-order and

fourth-order interference using photons from two nonlinear interaction regions, however, only single-frequency interference was observed in their experiment. Nevertheless, the ring-like

fringes created by interference using photons with the structured FAS remain unexplored, along with the properties of these fringes, and these fringes thus form the main topic of our study.

We also quantify the distribution of the fringes and their differences from the fringes obtained through traditional equal-inclination interference. In the following, we first introduce

briefly the experimental setup (details are presented in Methods), describe the FAS of the SPDC obtained from our experiment and present the expression for the tuning curve used for

nondegenerate type-0 quasi-phase-matching. Next, we explain how the interference fringes are generated and define the equivalent wavelength and parameter _γ_, which is the ratio of the real

centre wavelength to the equivalent wavelength, to show the difference between ASD and equal-inclination interference. Finally, we discuss the potential applications of this ASD interference

phenomenon. RESULTS In our experiment (Fig. 2), we use a periodically poled potassium titanyl phosphate (PPKTP) crystal as our SPDC source, which makes use of nondegenerate type-0

quasi-phase-matching35. The photons generated in SPDC and used for the interference are referred to as signal photons (with wavelengths of approximately 797 nm); the idler photons (~1540 nm)

are discarded. The FAS of the signal photon (Fig. 2a) is described by a binary function that reflects the radiation properties of the SPDC process. Its shape is parabolic with a width

having a sinc2 functional shape. The unique distribution of FAS is simulated based on the phase-matching condition (see Section 1 of Supplementary Information for details). The function

values of the FAS reflect the relative probability of photon detection for a particular outside angle (emission angle outside the crystal) and a particular frequency. If the phase-matching

condition is well satisfied, the value is relatively large. In other words, the smaller the phase mismatch is, the larger the value is, and vice versa. We assume photons with a FAS of Fig.

2a enter a Michelson interferometer having an arm difference _d_. Because each frequency component has a distinct interference result expressed by factor[1 + cos(2_dω_s/_c_)]/2, the FAS

after the interferometer becomes that shown in Fig. 2b (here, _d_ = 100 μm as an example). If the photons then pass through a lens that is used as a Fourier translator, each of their angular

components maps into a ring in the spatial domain. Therefore, a ring-like interference pattern is formed when the photons are observed. The setup of the Michelson interferometer in our

experiment (Fig. 2) comprises two lenses (L1 and L2) that form a 4-f imaging system and two mirrors (M1 and M2) located at the focal points. Another lens (L3) is used as a Fourier

translator, which maps the spatial frequency components to the spatial rings on the detection plane. The interference patterns, shown in Fig. 3a, are recorded by a photon-counting

intensified charge-coupled device (ICCD) camera. The simulations of the interference patterns from calculating the phase mismatch are shown in Fig. 3b (the simulation is based on equations

(S3) and (S6) in Section 2 of Supplementary Information, in which a small-angle approximation is used). The interference pattern may also be established from analytical methods. Here, we

ignore the width of the FAS (Fig. 2a), and we are only interested in parabola-like tuning curves that show how the outside angle of the signal photons changes as a function of frequency or

wavelength. The tuning curve is approximately described by the expressions (detailed derivations may be found in Section 3 of Supplementary) $$\theta _{{{{\mathrm{s - out}}}}}^2 = b_1\Delta

\omega$$ (1) $$b_1 = \frac{{2n_{i0}n_{{{{\mathrm{s}}}}0}\omega _{{{{\mathrm{i}}}}0}\left( {\beta _{{{\mathrm{s}}}}\omega _{{{{\mathrm{s}}}}0} + n_{{{{\mathrm{s}}}}0} - \beta

_{{{\mathrm{i}}}}\omega _{{{{\mathrm{i}}}}0} - n_{{{{\mathrm{i}}}}0}} \right)}}{{\omega _{{{{\mathrm{s}}}}0}\left( {\omega _{{{{\mathrm{s}}}}0}n_{{{{\mathrm{s}}}}0} + \omega

_{{{{\mathrm{i}}}}0}n_{{{{\mathrm{i}}}}0}} \right)}}$$ (2) where \(\Delta \omega = \omega _{{{\mathrm{s}}}} - \omega _{{{{\mathrm{s}}}}0} = \omega _{{{{\mathrm{i}}}}0} - \omega

_{{{\mathrm{i}}}}\), and \(\beta _{{{\mathrm{s}}}} = \left( {\frac{{dn}}{{d\omega _{{{\mathrm{s}}}}}}} \right)_{\omega _{{{{\mathrm{s}}}}0}},\;\beta _{{{\mathrm{i}}}} = \left(

{\frac{{dn}}{{d\omega _{{{\mathrm{i}}}}}}} \right)_{\omega _{{{{\mathrm{i}}}}0}}\) are the coefficients of first-order dispersion at the centre frequency of the signal and idler photons. The

subscript 0 indicates a corresponding value at the centre frequency of the wavelength; for example, _ω_s0,_ω_i0,_n_s0,_n_i0 are the centre frequency and the corresponding refractive index

of the signal and idler photons. Equations (1) and (2) were obtained by applying approximate conditions in which Δ_ω_ is small and the length of the crystal is long enough so that the width

of the FAS may be ignored. The relationship between radius _ρ_ of the abovementioned ring and the outside angle of signal photons is approximately given by _ρ_ _≈_ _θ_s_out_f_3, for which

_f_3 is the focal length of L3. By substituting Eq. (1) into the general interference factor [1 + cos(2_dω_s/_c_)]/2, the count recorded by the ICCD may be expressed as: $$C\left( \rho

\right) \propto 1 + \cos \left( {\frac{{2d\omega _{s0}}}{c} + \frac{{2d}}{{f_3^2b_1c}}\rho ^2} \right)$$ (3) The interference patterns predicted by Eq. (3) are presented in Fig. 3c. The

difference between Fig. 3b, c is that the simulations in Fig. 3c do not take the interference visibility into account because the width of the sinc2 function is ignored. In other words, the

complete interference expression should have the form [1 + _V_(_d_)cos(2_dω_s/_c_)]/2, where the function _V_(_d_) represents the interference visibility and _V_(_d_) is assumed to have a

constant value of 1 in Eq. (3). The interference visibility and the coherence length are described by Eq. (S22) and (S23) in Section 4 of Supplementary Information, respectively. In the

experiment, we fixed M2 on the displacement platform and M1 on the piezoelectric transducer (PZT). We varied the arm difference by moving M2, then finely adjusted the PZT to ensure the

centres of the interference patterns are bright spots. Fig. 3a shows the experimental results with different arm differences. The numbers at the top indicate approximate arm differences,

specifically, from the reading of the displacement platform. The numbers at the bottom of Fig. 3c show the actual arm differences set in the simulation. In comparison, the experimental

results agree well with our theoretical calculation. In Fig. 3a–c, more interference rings appear with increasing arm difference _d_. We next show the radial distribution of the rings as a

function of the arm difference. Assuming the radius of the _n_-th ring is _ρ__n_, (_n_ being the constructive interference order), then from Eq. (3) we obtain a quadratic relation $$a\rho

_n^2{{{\mathrm{ + }}}}\phi _0 = n$$ (4) where \(a = d/\pi f_3^2b_1c\) and _ϕ_0 = _dω_s0/_πc_. Equation (4) describes the distribution of fringes where the coefficient _a_ determines the

radius of the fringes for each order. For a specific order _n_, a greater value of _a_ indicates a smaller value of the radius ρ_n_ and thus indicates a higher fringe density. In the

experiments, _a_ is obtained by fitting the experimental data (ρ_n_,_n_). By comparing the coefficient _a_e = _d_/_f_2_λ_ for the far-field equal-inclination interference36,

(\(a_{{{\mathrm{e}}}} = d/f_3^2\lambda _{{{{\mathrm{s}}}}0}\) for our experimental condition), we define an equivalent wavelength _λ_eq = _πb_1_c_ to cause the coefficient _a_ to have the

general form \(a = d/f_3^2\lambda _{{{{\mathrm{eq}}}}}\). In the experiment, this equivalent wavelength is obtained by fitting the dependence of _a_ to _d_. Fig. 3d shows the experimentally

obtained pairs (ρ_n_,_n_) for different values of _d_. The coefficient _a_ may be evaluated using a second-order polynomial fit to the data. In Fig. 3e, the obtained values of _a_ are

plotted for different _d_. The red line shows the fitted result, from which one obtains the equivalent wavelength 29.38 nm, which agrees well with the predicted value of 29.86 nm. For

comparison, we also show the _a_e-_d_ relation (dashed line) of a traditional equal-inclination interference; the ratio of the slopes of the two lines is denoted _γ_ = _a/a__e_ = 

_λ_s0/_λ_eq. Except for the centre wavelength, _γ_ is also dependent on the key parameter _b_1, the value of which depends on properties of the crystal material. From a qualitative analysis

using Eq. (2), the determining factor for _b_1 includes the refractive index and crystal dispersion, the degree of degeneracy, and the type of quasi-phase-matching. The value of _γ_ can be

larger if the experimental parameters are carefully selected. DISCUSSION In summary, we report and study an interference phenomenon known as ASD interference using photons from one arm of an

SPDC source. In this type of interference, the fringes distribution in Eq. (4) is the same as that in equal-inclination interference, however, it varies more rapidly with the increasing

interferometer arm difference than those obtained from traditional equal-inclination interference. We defined two parameters to quantitatively compare the difference between the ASD

interference and the traditional equal-inclination interference: the equivalent wavelength _λ_eq and the ratio _γ_. Under our experimental conditions, _γ_ has an approximate value of 27;

this means that the fringe density is improved by 27-fold for a specific arm difference _d_, in other words, the fringes of this interference vary 27 times more rapidly than the traditional

equal-inclination interference with increasing arm difference. An advantage of the ASD interference is that the sensitivity can be increased _γ_-fold when we use this interferometer to

measure small displacements or refractive index changes by recording variations of fringes, because in these cases, greater variation in the fringes indicates better sensitivity for OPD.

Another advantage of ASD interference with large value of _γ_ is that the point at which the zero OPD occurs can be determined more accurately and thus the optical path measurement accuracy

can be improved. As shown in Fig. 3a–c, the first completely dark fringe occurs when _d_ = ±20 μm; this means that the position with the equivalent path can be determined with an error of

±20 μm; in the supplementary, we show that the error can be reduced to ±0.54 μm by fitting our experimental data. Furthermore, Eq. (3) indicates that the accuracy may be improved further by

expanding the field of view _ρ_max or reducing either the focal length of L3 or the equivalent wavelength _λ_eq. Because the SPDC source itself is a currently available nondegenerate

two-photon source, the potential applications of ASD interference can also be generalised to the nonlinear interferometers based on SPDC34,37,38. The ASD interference fringes not only have a

ring-like structure in intensity but also have a structure in frequency of photons, where the photons in the different fringes have different frequencies. Considering the frequency

structure, this interference phenomenon also holds promise in spectral-shaping a photon source based on SPDC. Because the rings in the interference patterns map different wavelength

components, a cosine-modulated frequency spectrum is obtained if the interference patterns are collected into multimode fibres. The interference phenomenon can be used in a reverse manner to

measure the tuning curve of the SPDC process. By fitting the equivalent wavelength, the parameter _b_1 of the tuning curve can then be obtained. Overall, the novel phenomenon reported here

not only enriches the existing knowledge with regard to interference and SPDC but also has promise for use in interferometry applications. MATERIALS AND METHODS PUMP LASER The 525.2-nm light

beam of the CW pump laser is generated in single-pass sum-frequency generation (SFG) with a 10-mm type-0 periodically poled potassium titanyl phosphate (PPKTP) crystal (the SFG source is

omitted in Fig. 2). In the SFG source, the wavelengths of the two pump beams are 1540 nm and 797 nm, and all three beams are vertically polarised. The SFG laser beam is collected into a

single-mode fibre and exits through a fibre collimator (the FC in Fig. 2). The idealised plane-wave pump in the SPDC leads to strict transverse momentum correlations. Therefore, the pump

beam is collimated by a lens group (the lens group is omitted in Fig. 2); its width is of order 400 μm and the pump power is 50 mW. The waveplates (Fig. 2) are used to transform the pump

beam from the collimator into a vertically polarised beam. CRYSTALS Two PPKTP crystals are used in the experiment, one for SFG and the other for SPDC. The two crystals have the same

parameter values: their dimensions are 1 mm × 2 mm × 10 mm, and their grating periods are 9.34 μm. The temperature of the crystal used during SFG is set at 24 °C, which is an optimum

temperature for SFG. The temperature of the crystal used for SPDC is set at 29 °C. This temperature is determined by performing difference-frequency generation between the 525.2-nm and

1540-nm laser beams. The two temperatures are different because the widths of the beams in the two crystals are different. OPTICAL SETUP Because the SPDC is the inverse of SFG, the central

wavelength of the idler and signal photons are approximately 1540 nm and 797 nm. The signal and idler photons are split through a long-pass dichroic mirror (DM), where the idler photons pass

through the DM (discarded) and the signal photons are reflected. The pump beam is filtered by a 750-nm long-pass filter that is omitted in Fig. 2. The experiment was performed in a dark

environment, and the light path in front of the camera was carefully shaded by a sealed box to block external light. DATA ACQUISITION The interference patterns (Fig. 3a) were recorded by our

ICCD camera (Andor iStar DH334T) with a 10 s exposure time. The working temperature of the ICCD is cooled at −25 °C. The background is taken before the data acquisition and is subtracted by

the ICCD camera automatically when signals are taken. The average counts of each pixel of the background are around 9000. The normalised grey values of the images in Fig. 3a from 0 to 1

represent the counts from 0 to 10000. REFERENCES * Jacques, V. et al. Experimental realization of Wheeler’s delayed-choice gedanken experiment. _Science_ 315, 966–968 (2007). Article  ADS 

Google Scholar  * Ionicioiu, R. & Terno, D. R. Proposal for a quantum delayed-choice experiment. _Phys. Rev. Lett._ 107, 230406 (2011). Article  ADS  Google Scholar  * Zhou, Z. Y. et al.

Quantum twisted double-slits experiments: confirming wavefunctions’ physical reality. _Sci. Bull._ 62, 1185–1192 (2017). Article  Google Scholar  * Hong, C. K., Ou, Z. Y. & Mandel, L.

Measurement of subpicosecond time intervals between two photons by interference. _Phys. Rev. Lett._ 59, 2044–2046 (1987). Article  ADS  Google Scholar  * Brown, R. H. & Twiss, R. Q.

Correlation between photons in two coherent beams of light. _Nature_ 177, 27–29 (1956). Article  ADS  Google Scholar  * Gossman, D. et al. Optical interference with digital holograms. _Am.

J. Phys._ 84, 508–516 (2016). Article  ADS  Google Scholar  * Santarsiero, M. & Gori, F. Spectral changes in a young interference pattern. _Phys. Lett. A_ 167, 123–128 (1992). Article 

ADS  Google Scholar  * Wood, R. W. XLV. Some new cases of interference and diffraction. _Lond., Edinb., Dublin Philos. Mag. J. Sci._ 7, 376–388 (1904). Article  Google Scholar  * Jack, B.,

Padgett, M. J. & Franke-Arnold, S. Angular diffraction. _N. J. Phys._ 10, 103013 (2008). Article  Google Scholar  * Forbes, A., De Oliveira, M. & Dennis, M. R. Structured light.

_Nat. Photonics_ 15, 253–262 (2021). Article  ADS  Google Scholar  * Abbott, B. P. et al. Observation of gravitational waves from a binary black hole merger. _Phys. Rev. Lett._ 116, 061102

(2016). Article  ADS  MathSciNet  Google Scholar  * Huang, D. et al. Optical coherence tomography. _Science_ 254, 1178–1181 (1991). Article  ADS  Google Scholar  * Stuart, B. H. Infrared

Spectroscopy: Fundamentals and Applications. (Hoboken: John Wiley & Sons, 2004). * Bergh, R. A., Lefevre, H. C. & Shaw, H. J. All-single-mode fiber-optic gyroscope. _Opt. Lett._ 6,

198–200 (1981). Article  ADS  Google Scholar  * Born, M. & Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. (Oxford: Pergamon

Press, 1964). * Harris, S. E., Oshman, M. K. & Byer, R. L. Observation of tunable optical parametric fluorescence. _Phys. Rev. Lett._ 18, 732–734 (1967). Article  ADS  Google Scholar  *

Burnham, D. C. & Weinberg, D. L. Observation of simultaneity in parametric production of optical photon pairs. _Phys. Rev. Lett._ 25, 84–87 (1970). Article  ADS  Google Scholar  * Zou,

X. Y., Wang, L. J. & Mandel, L. Induced coherence and indistinguishability in optical interference. _Phys. Rev. Lett._ 67, 318–321 (1991). Article  ADS  Google Scholar  * Strekalov, D.

V. et al. Observation of two-photon “ghost” interference and diffraction. _Phys. Rev. Lett._ 74, 3600–3603 (1995). Article  ADS  Google Scholar  * Kim, Y. H. et al. Delayed “choice” quantum

eraser. _Phys. Rev. Lett._ 84, 1–5 (2000). Article  ADS  Google Scholar  * Gisin, N. et al. Quantum cryptography. _Rev. Mod. Phys._ 74, 145–195 (2002). Article  ADS  Google Scholar  *

Jennewein, T. et al. Quantum cryptography with entangled photons. _Phys. Rev. Lett._ 84, 4729–4732 (2000). Article  ADS  Google Scholar  * Pittman, T. B. et al. Optical imaging by means of

two-photon quantum entanglement. _Phys. Rev. A_ 52, R3429–R3432 (1995). Article  ADS  Google Scholar  * Bouwmeester, D. et al. Experimental quantum teleportation. _Nature_ 390, 575–579

(1997). Article  ADS  Google Scholar  * Boschi, D. et al. Experimental realization of teleporting an unknown pure quantum state via dual classical and einstein-podolsky-rosen channels.

_Phys. Rev. Lett._ 80, 1121–1125 (1998). Article  ADS  MathSciNet  Google Scholar  * Kok, P. et al. Linear optical quantum computing with photonic qubits. _Rev. Mod. Phys._ 79, 135–174

(2007). Article  ADS  Google Scholar  * Nagata, T. et al. Beating the standard quantum limit with four-entangled photons. _Science_ 316, 726–729 (2007). Article  ADS  Google Scholar  *

Lemos, G. B. et al. Quantum imaging with undetected photons. _Nature_ 512, 409–412 (2014). Article  ADS  Google Scholar  * Liu, L. Z. et al. Distributed quantum phase estimation with

entangled photons. _Nat. Photonics_ 15, 137–142 (2021). Article  ADS  Google Scholar  * Zhong, H. S. et al. Quantum computational advantage using photons. _Science_ 370, 1460–1463 (2020).

Article  ADS  Google Scholar  * Shih, Y. Entangled biphoton source-property and preparation. _Rep. Prog. Phys._ 66, 1009–1044 (2003). Article  ADS  MathSciNet  Google Scholar  * Shih, Y. An

Introduction to Quantum Optics: Photon and Biphoton Physics. (Boca Raton: CRC Press, 2011), 484. * Stöhr, J. Overcoming the diffraction limit by multi-photon interference: a tutorial. _Adv.

Opt. Photonics_ 11, 215–313 (2019). Article  ADS  Google Scholar  * Burlakov, A. V. et al. Interference effects in spontaneous two-photon parametric scattering from two macroscopic regions.

_Phys. Rev. A_ 56, 3214–3225 (1997). Article  ADS  Google Scholar  * Boyd, R. W. Nonlinear Optics. 3th edn. (Amsterdam: Elsevier, 2008). * Hochrainer, A. et al. Interference fringes

controlled by noninterfering photons. _Optica_ 4, 341–344 (2017). Article  ADS  Google Scholar  * Kviatkovsky, I. et al. Microscopy with undetected photons in the mid-infrared. _Sci. Adv._

6, eabd0264 (2020). Article  Google Scholar  * Chekhova, M. V. & Ou, Z. Y. Nonlinear interferometers in quantum optics. _Adv. Opt. Photonics_ 8, 104–155 (2016). Article  ADS  Google

Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the National Natural Science Foundation of China (NSFC) (61605194, 11934013, 61525504), the Anhui Initiative In

Quantum Information Technologies (AHY020200), the China Postdoctoral Science Foundation (2017M622003, 2018M642517). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * CAS Key Laboratory of

Quantum Information, University of Science and Technology of China, Hefei, Anhui, China Chen Yang, Zhi-Yuan Zhou, Yan Li, Shi-Kai Liu, Zheng Ge, Guang-Can Guo & Bao-Sen Shi * Synergetic

Innovation Center of Quantum Information & Quantum Physics, University of Science and Technology of China, Hefei, Anhui, China Chen Yang, Zhi-Yuan Zhou, Yan Li, Shi-Kai Liu, Zheng Ge, 

Guang-Can Guo & Bao-Sen Shi Authors * Chen Yang View author publications You can also search for this author inPubMed Google Scholar * Zhi-Yuan Zhou View author publications You can also

search for this author inPubMed Google Scholar * Yan Li View author publications You can also search for this author inPubMed Google Scholar * Shi-Kai Liu View author publications You can

also search for this author inPubMed Google Scholar * Zheng Ge View author publications You can also search for this author inPubMed Google Scholar * Guang-Can Guo View author publications

You can also search for this author inPubMed Google Scholar * Bao-Sen Shi View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS C.Y., Z.-Y.Z.,

and B.-S.S. conceived the research and designed the experiments. C.Y. performed the experiments and numerical simulations. The data acquisition and processing were performed by C.Y. with

help from Y.L., S.-K.L., and Z.G., Z.-Y.Z., G.-C.G, and B.-S.S. supervised the project. All authors contributed to the discussion of experimental results. C.Y., Z.-Y.Z., and B.-S.S. wrote

the manuscript with contributions from all co-authors. CORRESPONDING AUTHORS Correspondence to Zhi-Yuan Zhou or Bao-Sen Shi. ETHICS DECLARATIONS CONFLICT OF INTEREST The authors declare no

competing interest. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIALS RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International

License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source,

provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons

license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Yang, C., Zhou, ZY., Li, Y. _et al._ Angular-spectrum-dependent interference.

_Light Sci Appl_ 10, 217 (2021). https://doi.org/10.1038/s41377-021-00661-z Download citation * Received: 29 March 2021 * Revised: 30 September 2021 * Accepted: 11 October 2021 * Published:

26 October 2021 * DOI: https://doi.org/10.1038/s41377-021-00661-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative