Reader TTS

ABSTRACT Viscous electron fluids have emerged recently as a new paradigm of strongly-correlated electron transport in solids. Here we report on a direct observation of the transition to this

long-sought-for state of matter in a high-mobility electron system in graphene. Unexpectedly, the electron flow is found to be interaction-dominated but non-hydrodynamic (quasiballistic) in

a wide temperature range, showing signatures of viscous flows only at relatively high temperatures. The transition between the two regimes is characterized by a sharp maximum of negative

resistance, probed in proximity to the current injector. The resistance decreases as the system goes deeper into the hydrodynamic regime. In a perfect darkness-before-daybreak manner, the

interaction-dominated negative response is strongest at the transition to the quasiballistic regime. Our work provides the first demonstration of how the viscous fluid behavior emerges in an

interacting electron system. SIMILAR CONTENT BEING VIEWED BY OTHERS OBSERVATION OF GIANT AND TUNABLE THERMAL DIFFUSIVITY OF A DIRAC FLUID AT ROOM TEMPERATURE Article Open access 23 August

2021 IMAGING VISCOUS FLOW OF THE DIRAC FLUID IN GRAPHENE Article 22 July 2020 IMAGING HYDRODYNAMIC ELECTRONS FLOWING WITHOUT LANDAUER–SHARVIN RESISTANCE Article 07 September 2022

INTRODUCTION Electron fluids, an exotic state of matter in which electron–electron (ee) interactions dominate transport, have been long anticipated

theoretically1,2,3,4,5,6,7,8,9,10,11,12,13,14,15 but until recently they were far from experimental reality. This situation is currently changing owing to the discovery of new materials in

which ee interactions are particularly strong or momentum relaxation due to disorder and phonons is weak. The inventory of experimental systems that can host viscous e-fluids, as we will

call them for brevity, has been steadily growing in the last few years16,17,18,19, stimulating wide interest in their properties. E-fluids may exhibit new behaviors such as vortices20,21,

whirlpools16, superballistic transport22,23, Poiseuille flow10,11,13,14,18, anomalous heat conduction17, and viscous magnetotransport24,25. The questions about the genesis of e-fluids, on

the other hand, received relatively little attention. How does an electron system enter the fluid state? What happens when _l_ee becomes comparable or larger than the system dimensions? What

is the relation between electric current and potential at the transition? All these questions are at present poorly understood: neither there exists a detailed theory treating both

ballistic and viscous electron regimes on equal footing, nor any systematic experimental study of the transition has been performed. Searching for the fluidity onset is the subject of this

work. So far, the behavior of e-fluids was mostly discussed deep in the hydrodynamic regime, where the mean free path _l_ee was the shortest lengthscale of the system. However, the

experimental conditions are usually such that _l_ee, tunable by varying temperature _T_, is either comparable or at most a few times smaller than the system dimensions, putting the

experimentally investigated e-fluids close to the onset of fluidity. As we will show below, this regime hosts an interaction-dominated quasiballistic state, which exhibits a negative voltage

response similar to that observed at not-too-high _T_ in the ref.16. The negative response arises because ambient carriers, as a result of momentum-conserving collisions with injected

carriers, are blocked from reaching voltage probes. Furthermore, the negative response is enhanced by “memory effects”, so that it may exceed the negative response in the viscous state26.

Thus, the interaction-dominated quasiballistic state, while quite distinct from the viscous fluid state, can in some cases serve as a proxy for the latter. Graphene offers a convenient venue

for this study. First, due to their exceptional cleanness and weak electron–phonon (el–ph) coupling, state-of-the-art graphene devices support micrometer-scale ballistic transport with

respect to momentum-non-conserving collisions over a wide range of temperatures27, from liquid-helium to room _T_. Second, above the temperatures of liquid nitrogen, ee collisions become the

dominant scattering mechanism, so that the behavior of the electron system resembles that of viscous fluids16,23. Third, _l_ee in graphene can be varied over a wide range23 by changing the

carrier density _n_ and _T_. This enables a smooth transition (or, more precisely, a crossover) between single-particle ballistic and viscous transport regimes, allowing us to track how the

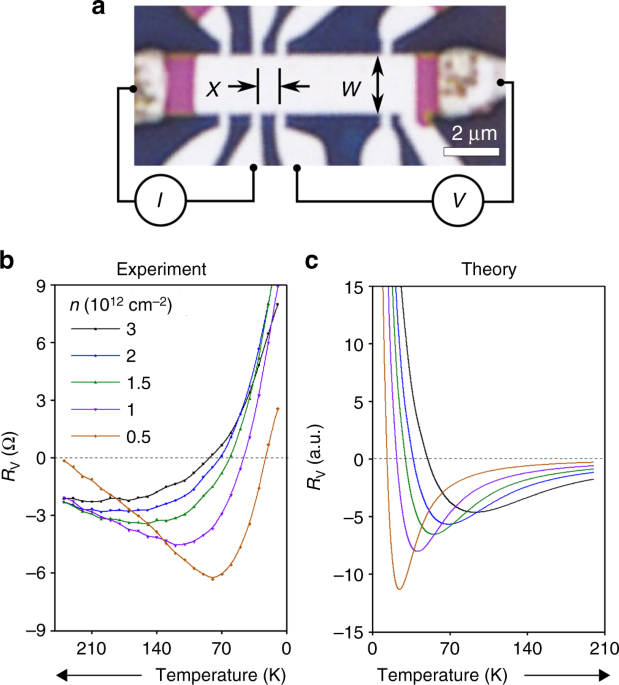
electron system enters the collective fluid state. RESULTS EXPERIMENTAL DATA We explore the onset of the hydrodynamic state by studying graphene devices in the so-called vicinity geometry16,

illustrated in Fig. 1a: The current _I_ is injected through a narrow contact into a wide graphene channel, and a local potential is probed at a small distance _x_ from the injector. The

main result of our study is that the vicinity resistance _R_v = _V_/_I_ reaches an extreme negative value at the onset of fluidity. In particular, this behavior manifests itself most clearly

through the temperature dependence of _R_v (Fig. 1b, c), with the quasiballistic and hydrodynamic regimes occurring at low and high _T_, respectively. We will show that the deep minimum at

intermediate temperatures in the _R_v (_T_) dependences is the hallmark of the transition. Furthermore, we will demonstrate that this transition can be conveniently quantified by the

electron Knudsen number $${\mathrm{Kn}} = l_{{\mathrm{ee}}}/x,$$ (1) taking values \({\mathrm{Kn}} \ll 1\) and Kn > 1 in the hydrodynamic and quasiballistic transport regimes,

respectively, and approaching unity at the fluidity onset. Importantly, the negative sign of _R_v, observed across the entire transition, signals that ee interactions dominate transport in

both the quasiballistic and hydrodynamic regimes. The hydrodynamic regime, where theory predicts d_R_v/d_T_ > 020,28, occurs only at high enough temperatures and low enough carrier

densities. This regime is preceded by an extended quasiballistic regime with d_R_v/d_T_ < 0, discussed in detail below. The occurrence of two distinct interaction-dominated regimes in a

2D electron system is a surprising finding, which is of interest from a fundamental perspective and important for possible applications. To explore the onset of the fluid state

experimentally, we fabricated high-quality devices based on bilayer graphene (BLG) encapsulated between hexagonal boron nitride (for details, see Methods). The latter provides a clean

environment for graphene’s electron system ensuring micrometer-scale ballistic transport with respect to extrinsic momentum-non-conserving scatterering. The devices were shaped in a form of

dual-gated multiterminal Hall bars (Fig. 1a), allowing us to study the distance-dependent potential anticipated at the transition upon varying the carrier densities _n_. The dual-gated

design allowed us to maintain zero displacement between the graphene layers, so that one could tune the Fermi energy _ε_F in BLG without altering its band structure (opening the band gap).

We have strategically chosen the BLG system because it _ε_F varies with _n_ stronger than in monolayer graphene (MLG) (_n_ vs. _n_1/2). The standard dependence _l_ee = ℏ_v_F_ε_F/(_k__B__T_)2

translates into the scaling _l_ee ∼ _n_3/2, which is much faster than the _n_1/2 dependence in MLG. This allowed us to explore a wider range of _l_ee than in MLG by varying the carrier

density for a given _T_ (see below), providing a convenient knob to tune the Kn value and probe the quasiballistic-to-hydrodynamic transition29. Notably, the signal measured in the vicinity

configuration contains a non-negligible offset due to momentum-non-conserving scattering (by phonons and/or disorder) which we further refer to as an Ohmic contribution. To distill the

viscous contribution, we employed the approach introduced in the ref. 16 in which the Ohmic term, expressed as _bρ_, was subtracted from the measured vicinity signal, assuming the additive

behavior of these contributions28. Here _ρ_ = _ρ_(_n_, _T_) is the BLG sheet resistance measured in the conventional four-terminal geometry and _b_ is the geometric factor that depends on

sample dimensions and the distance between the injection point and the voltage probe16,28 (for example, _b_ = 0.1 for the measurementent configuration shown in Fig. 1a). As discussed below,

the procedure of subtracting the Ohmic contribution, while somewhat ad hoc, can be justified for the geometry of our experiment. Below we refer to this adjusted vicinity resistance using the

same notation _R_v unless stated otherwise. Figure 1b shows _R_v as a function of _T_ measured in one of our BLG devices. Far away from the charge neutrality point (CNP) and at liquid

helium _T_, _R_v is positive for all experimentally accessible _n_. When the temperature is increased, _R_v rapidly drops, reverses its sign, reaches a minimum and then starts to grow.

Figure 2a details this observation by mapping _R_v on the (_n_, _T_)-plane. The non-monotonic dependence _R_v vs. _T_ is observed for all _n_, whereby the temperature at which _R_v dips,

grows with increasing _n_ (red dashed line). To understand this nonmonotonic behavior, we first consider the limiting cases: the hydrodynamic regime \(l_{{\mathrm{ee}}} \ll x\), realized at

large _T_, and the free-particle regime \(l_{{\mathrm{ee}}} \gg W\), realized at the lowest _T_ (here _W_ is the device width). In the hydrodynamic regime, negative _R_v arises as a result

of viscous entrainment by the injected current of the fluid in adjacent regions16,20,28. In the free-particle regime, positive _R_v is expected from single-particle ballistic transport due

to reflection of injected carriers from the opposite boundaries30,31. Therefore, the sign of _R_v must change from negative to positive upon lowering _T_, as indeed seen in the data shown in

Fig. 1a. Furthermore, the hydrodynamic _R_v is proportional to viscosity20,28, giving the dependence \(R_{\mathrm{v}}\sim l_{{\mathrm{ee}}}(T)\). The quantity _l_ee(_T_) increases as _T_

decreases, leading to increasingly more negative _R_v. The non-monotonic temperature dependence _R_v(_T_), implied by these observations, is indeed seen in our measurements (Figs. 1b, 2a).

Importantly, in between the free-particle regime \(l_{{\mathrm{ee}}} \gg W\) and the hydrodynamic regime \(l_{{\mathrm{ee}}} \gg x\) lies an interesting regime _x_ < _l_ee < _W_ that

has hitherto been ignored in the literature. This intermediate regime, which for the lack of a better name will be called “quasiballistic”, features an interaction-dominated response of a

non-hydrodynamic nature, since the mean free path _l_ee is greater than the distance from the injector to the probe. Conspicuously, _R_v remains negative in this regime. However, since now

\(R_{\mathrm{v}}\sim 1/l_{{\mathrm{ee}}}(T)\), the sign of d_R_v/d_T_ is reversed compared to the hydrodynamic regime. The negative sign of _R_v can be understood by considering injected

carriers that travel over a large distance of the order of _l_ee > _x_ and then scatter off ambient thermal carriers. After scattering, some of the injected carriers make it back into the

probe, creating a positive contribution to _R_v. Simultaneously, some of the ambient carriers, through scattering off the injected carriers, are blocked from reaching the probe. This

process creates a negative contribution to _R_v. Detailed analysis shows that the latter contribution dominates26, giving rise to negative _R_v. As _T_ increases, _R_v grows progressively

more negative until the point _l_ee = _x_, where the hydrodynamic behavior sets in and the sign of the _T_ dependence is reversed. Interestingly, in the quasiballistic regime, the value

|_R_v| decreases with _n_ and grows with _T_, in qualitative agreement with the behavior of a MLG _R_v at not-too-high _T_ found in the ref. 16. This suggests a possible resolution of the

conundrum posed by the findings of ref. 16, in which a hydrodynamic-like negative _R_v was found to depend on _n_ and _T_ differently from what is expected in the hydrodynamic regime. THEORY

AND COMPARISON WITH EXPERIMENT To capture all these different regimes in a single model, we employ the kinetic equation for quasiparticles in the graphene Fermi liquid. Transport in the

geometry of Fig. 1 is described by solving the kinetic equation in an infinite strip of width _W_: −∞ < _x_ < ∞, 0 < _y_ < _W_, with diffuse boundary conditions at the strip

edges _y_ = 0, _W_. Current _I_ is injected through a point-like source at _x_ = _y_ = 0 and is drained on the far left, _x_ = −∞. We find the potential at (_x_, 0) by evaluating the

particle flux entering the probe (for details, see Methods). At low temperatures the ee rate _γ_ee is small, and the ee collision term can be ignored12. The model then describes ballistic

particles bouncing between the strip edges, as illustrated in the upper inset of Fig. 3b. The net flux of particles into the probe then gives a positive value _R_v = _V_p(_x_)/_I_. At high

_T_, on the other hand, the ee collision term dominates, and the distribution function approaches the local equilibrium. The resulting hydrodynamic behavior is then described by the Stokes

equation that states the balance between the viscous friction and electric forces: _e_E/_m_ = −_ν_▽2V. (The latter follows directly from the Eq. (12) of Methods, multiplied by P, integrated

over momenta and combined with an expression for the stress tensor obtained from 1/_γ_ee expansion.) In this case, we obtain \(R_{\mathrm{v}}\sim \eta /(nex)^2\), where _η_ is the dynamic

viscosity given by \(\eta = \frac{1}{4}m^ \ast nv_{\mathrm{F}}l_{{\mathrm{ee}}}\) and _m_* is the carrier effective mass20,22. The single parameter _γ_ee allows us to explore both the

ballistic and viscous regime through the dependence of _R_v on _T_ and _n_. Carrier dynamics in the quasiballistic regime is shown schematically in the lower inset of Fig. 3b. In Fig. 1b, c

we compare the experimental data for _R_v vs. _T_ with the results of our modeling, assuming the ee collision rate that depends on _T_ and _n_ as \(\hbar \gamma _{{\mathrm{ee}}}\sim

T_e^2/\varepsilon _{\mathrm{F}}\) 12. For bilayer graphene, the Fermi energy _ε_F is related to the carrier density as _n_ = _m_*_ε_F/(_π_ℏ2), where _m_* = 0.033 _m_e. The two panels flaunt

good qualitative agreement; namely, our theory captures the main experimental features: positive _R_v at small _T_ that rapidly drops with increasing _T_ and monotonically grows with _n_, so

that the minima and sign changes in _R_v occur at higher _T_ for larger _n_. Furthermore, our model reproduces some of the more subtle features of the data. For example, the nodes in _R_v

vs. _T_ shift to higher _T_ and the minima to lower _T_, as the distance to the probe _x_ increases, see Fig. 3. An overall agreement is also found for the full _R_v(_n_, _T_) maps shown in

Fig. 2a, b that become near-identical after rescaling the _T_ axis. DISCUSSION In our analysis, for simplicity, we disregarded the Ohmic effects due to the el-ph scattering. This is a

reasonable starting point since the el-ph scattering mean free path _l_el−ph is considerably larger than _l_ee at the temperatures of interest (for details, see Methods). However, the flow

can be distorted by the Ohmic effects at the lengthscales set by \(\xi = \sqrt {\eta /n^2e^2\rho } = \frac{1}{2}\sqrt {l_{{\mathrm{el}} - {\mathrm{ph}}}l_{{\mathrm{ee}}}}\), which lies

between _l_ee and _l_el−ph20,21. Thus caution must be exercised even when the el-ph scattering is weak. The procedure of extracting the viscous contribution by subtracting the Ohmic

contribution is expected to work well so long as the Ohmic effects do not distort the current flow at the lengthscales which are being probed, i.e. when _ξ_ exceeds the distance to the probe

_x_ ≈ 1 μm. Estimates show that the inequality \(\xi \gg x\) holds at not-too-high temperatures, i.e. in the quasiballistic regime. At the fluidity onset, identified above as the turning

point in the _R_v(_T_) dependence, for the estimated typical values \(l_{{\mathrm{ee}}} \lesssim 0.2\) μm and \(l_{{\mathrm{el}} - {\mathrm{ph}}}\sim 3\,{\mathrm{\mu m}}\), the lengthscale

_ξ_ can become comparable to _x_. However, an analysis based on the Stokes equation indicates that, for the geometry of our experiment, the Ohmic and viscous contributions remain

approximately additive even for _ξ_ < _x_ (for details, see Methods). We therefore believe that the subtraction procedure provides a reasonable approximation in the entire range of

temperatures and dopings. We also note that Figs. 2, 3 exhibit some discrepancy between the values of _T_ at which theoretical and experimental _R_v reach the minimum. This is not

particularly surprising given the simplistic expression of \(\gamma _{{\mathrm{ee}}}\sim T^2\) used in the model. Since _γ_ee is the only relevant temperature-dependent parameter in the

model, the quantitative agreement can be improved through revising the dependence _γ_ee vs. _T_. Indeed, there are various effects that can give rise to deviation from the standard

Fermi-liquid _T_2 dependence. One is the logarithmic enhancement of the quasiparticle decay rate due to collinear ee collisions32,33,34. However, it is probably an unlikely culprit, since

collinear collisions do not lead to angular relaxation. At the same time, recent analysis35 indicates that the effective _γ_ee that determines electron viscosity depends on the lifetimes of

the odd-_m_ angular harmonics, _m_ = ±3, ±5,..., which relax considerably slower than the Fermi-liquid _T_2 estimate would suggest. Accounting for this effect could, effectively, extend the

quasiballistic behavior to higher temperatures, which would improve the agreement with the observed dependence _R_v(_T_). Detailed analysis of these rates and of their impact on _R_v is

beyond the scope of this work. The experimental and theoretical _R_v(_T_) exhibit two prominent features: _R_v first changes sign from positive to negative and then passes through a deep

minimum. Should the sign change or the minimum be taken as the signature of the onset of fluidity? That question can be answered with the help of the data presented in Fig. 3, demonstrating

that _R_v is a non-trivial function of both _l_ee/_W_ and _l_ee/_x_. We note in that regard that the sign reversal of theoretically computed _R_v occurs at \({\mathrm{Kn}} \gg 1\), that is

inside the quasiballistic regime, for all values of _x_ (Fig. 3b). Indeed, _R_v in Fig. 3b changes sign at _T_ = 20 K which for a given _n_ translates into _l_ee ≈ 10 μm, a length scale

significantly greater than the values \(x\sim 1 - 2\) μm for this device. On the other hand, the most negative _R_v in Fig. 3b is found at Kn = 1–3, which corresponds to \(x\sim

l_{{\mathrm{ee}}} < W\). Since in the hydrodynamic regime _R_v is proportional to _η_ and thus should drop with increasing _T_, we infer that it is the condition \({\mathrm{Kn}} \sim 1\)

(where _R_v is most negative) that describes the fluidity onset. Furthermore, _R_v is expected to be negative in the quasiballistic regime26 when Kn > 1, so it is indeed the drop of

|_R_v| with temperature, rather than the sign reversal, that marks the onset of the viscous flow. Experimental observation of this anomalous behavior at the onset of the fluid state enables

a direct electrical measurement of the mean free path _l_ee and electron viscosity. Good qualitative agreement of the experimental data and our theoretical model suggests further

opportunities to study the physics of e-fluids, in particular the electron transport in the presence of magnetic field and/or confining potential, obstacles, funnels and electron pumps. Our

work clearly shows that the initial deviation from the ballistic behavior observed experimentally in different systems13,14,16,18,23 may be due to an entry into the interaction-dominated

“quasiballistic” regime rather than the true onset of electron fluidity. It requires higher temperatures and the observation of the behavior consistent with viscosity gradually decreasing

with increasing _T_ to ascertain that the Navier-Stokes description can be applied. METHODS DEVICE FABRICATION Our devices were made of bilayer graphene encapsulated between ≈50 nm-thick

crystals of hexagonal boron nitride (hBN). The hBN-graphene-hBN heterostructures were assembled using the dry-peel technique described elsewhere27,36 and deposited on top of an oxidized Si

wafer (290 nm of SiO2) which served as a back gate. After this, a PMMA mask was fabricated on top of the hBN-graphene-hBN stack by electron-beam lithography. This mask was used to define

contact areas to graphene, which was done by dry etching with fast selective removal of hBN37. Metallic contacts (usually, 5 nm of chromium followed by 50 nm gold) were then deposited onto

exposed graphene edges that were a few nm wide. As the next step, another round of electron-beam lithography was used to prepare a thin metallic mask (40 nm Al) which defined a multiterminal

Hall bar. After this, reactive ion plasma etching translated the shape of the metallic mask into encapsulated graphene. The Al mask also served as a top gate, in which case Al was

wet-etched near the contact leads to remove the electrical contact to graphene. DISTILLING THE HYDRODYNAMIC CONTRIBUTION IN THE PRESENCE OF OHMIC EFFECTS Here we assess the accuracy of the

approach used in the main text to separate the viscous and Ohmic contributions to the _R_v signal. In this approach, it was assumed that the contributions are approximately additive, and

thus the viscous contribution can be distilled by subtracting the (suitably scaled) Ohmic resistivity measured in a four-probe setup. The validity of the additivity assumption can be

verified using an exact solution of the hydrodynamic equations for current injected in a halfplane. The hydrodynamic approach applies when the ee mean free path is smaller than the el-ph

scattering mean free path, \(l_{{\mathrm{ee}}} \ll l_{{\mathrm{el}} - {\mathrm{ph}}}\). At the scales larger than _l_ee the electron flow satisfies the Stokes equation with an Ohmic term

added to describe momentum relaxation: $$\left( {\eta \nabla ^2 - n^2e^2\rho } \right){\mathrm{v}} = ne\nabla \phi$$ (2) Taking a curl and defining _κ_2 = _ρ_(_en_)2/_η_ = 1/_ξ_2, we obtain

the equation on the stream function: $$\left( {\nabla ^4 - \kappa ^2\nabla ^2} \right)\psi = 0,$$ (3) where _v_ = ∇ × (_ψ_Z). Following21, we consider the flow in a half-plane _y_ > 0

generated by the a point source on the boundary at _x_ = 0: _ψ__x_(_x_, 0) = _δ_(_x_)_I_/_ne_. The stream function in this case has the form $$\psi (x,y) = \frac{I}{ne}{\int}

\frac{e^{ikx}{\mathrm{d}}k}{2\pi ik}\left[ {Ae^{ - |k|y} + (1 - A)e^{ - qy}} \right],$$ (4) where we defined \(q = \sqrt {k^2 + \kappa ^2} > 0\). The stream function can be used to

evaluate the potential. Plugging Eq. (4) in Eq. (2), we see that only the first (harmonic) term in the stream function contributes the potential: $$\nabla \phi = \frac{\eta }{{en}}(\nabla ^2

- \kappa ^2){\mathbf{v}} = \frac{\eta }{{en}}(\nabla ^2 - \kappa ^2){\mathbf{z}} \times \nabla \psi = - \frac{{\eta I\kappa ^2}}{{2\pi (en)^2}}{\mathbf{z}} \times \nabla {\int}

\frac{{Ae^{ikx - |k|y}{\mathrm{d}}k}}{{ik}}.$$ (5) The yet-undetermined quantity _A_(_k_) depends on the type of boundary condition. The no-stress boundary condition at _y_ = 0, which reads

_ψ__yy_(_x_, 0) = 0, yields _A_(_k_) = _q_2/_κ_2 = 1 + _k_2/_κ_2. Remarkably, the exact potential is a sum of the viscous and Ohmic contributions, with each contribution unaffected by the

presence of the other contribution in this case: $$\phi (x,y) = \frac{I}{{2\pi }}\left[ {\frac{{2\eta }}{{(en)^2}}y^2 - x^2\left( {x^2 + y^2} \right)^2 + \rho {\mathrm{log}}\left(

{\frac{{L^2}}{{x^2 + y^2}}} \right)} \right],$$ (6) where _L_ is the system size. The subtraction procedure employed in analyzing the measurements is exact at all distances for the no-stress

boundary condition. For the no-slip boundary condition, on the other hand, the additivity is only an approximate property. In this case, _ψ__y_(_x_, 0) = 0 gives $$A(k) = 1 + k^2/\kappa ^2

+ q|k|/\kappa ^2.$$ (7) The last term in this expression gives a contribution which depends both on viscosity and resistivity. As illustrated in Fig. 4, this contribution is non-negligible

at distances \(x \simeq \xi\), where _R_v changes sign. Its magnitude, however, is small (under 10–15% of the total potential). Therefore, disregarding this contribution should provide a

reasonably good approximation. Yet, this conclusion is almost certainly geometry-sensitive, being valid for the point source at a halfplane edge but not necessarily for other geometries.

ESTIMATES OF THE ELECTRON-PHONON SCATTERING MEAN FREE PATH Electron-phonon scattering rate in graphene was discussed mostly for the single-layer case38,39,40. Here we modify this analysis

for the bilayer case. The value of the mean free path _l_el−ph is used in the main text to determine the lengthscales at which the the el-ph scattering does not distort the carrier flow. We

use the standard deformation potential Hamiltonian $$H_{\mathrm{el - ph}} = {\int} {\mathrm{d}}^2r\psi ^\dagger ({\mathbf{r}},t)D\nabla {\mathbf{u}}({\mathbf{r}},t)\psi ({\mathbf{r}},t),\\

{\mathbf{u}} = \mathop {\sum}\limits_{\mathrm{k}} \sqrt {\frac{\hbar }{{2\rho \omega _{\mathrm{k}}}}} \left( {b_ke^{i{\mathbf{kr}} - i\omega _{\mathbf{k}}t} + b_{ - {\mathbf{k}}}^\dagger e^{

- i{\mathbf{k}}r + i\omega _{\mathbf{k}}t}} \right),$$ (8) where U(R, _t_) is the lattice displacement vector, _D_ is the deformation potential coupling constant, _ω_K = _s_|K| is the

phonon frequency, and _ρ_ is the surface mass density of graphene sheet. Plugging these quantities into the Golden Rule for the el-ph emission rate gives $${\mathrm{d}}{\mathrm{\Gamma }} =

\frac{{\mathrm{d}\theta }}{{2\pi }}\nu \left| {V_{fi}} \right|^2\frac{{2\pi }}{\hbar }\left( {N_{{\mathrm{ph}}}(\mathbf{k}) + 1} \right),$$ (9) where _θ_ is the angle parameterizing the

Fermi surface, and the deformation potential matrix element equals \(\left| {V_{fi}} \right| = \sqrt {\frac{\hbar }{{2\rho \omega _{\mathbf{k}}}}} D{\kern 1pt} |{\mathbf{k}}|{\kern 1pt}

\left\langle {\psi _f|\psi _i} \right\rangle\), with the overlap 〈_ψ__f__|ψ__i_〉 = cos(_θ_P′ − _θ_P) accounting for the chirality of charge carriers. Here P and P′ are electron momenta, and

K = P − P′. (Parenthetically, for monolayer graphene, the cos factor is to be replaced with cos((_θ_P′ − _θ_P)/2).) The density of final states equals _ν_ = _m_*/(2_π_ℏ2), where _m_* = 0.033

 _m_e is the carrier effective mass; since electron–phonon scattering preserves carrier spin and valley index, the relevant degeneracies are not included in _ν_. Phonon absorption is

described by a similar expression with _N_ph(K) + 1 replaced by _N_ph(K). Since temperatures of interest are considerably larger than the Bloch-Gruneisen temperature _T_BG = ℏ_sk_F, we can

approximate the Bose factors _N_ph(K) and _N_ph(K) + 1 as _T_/ℏ_ω_K. Plugging _N_ph(K) + _N_ph(K) + 1 ≈ 2_T_/ℏ_ω_K in the expression for _d_Γ and replacing _k_ with P − P′, gives

$${\mathrm{d}}{\mathrm{\Gamma}} = {\mathrm{cos}}^2(\theta )\frac{{\mathrm{d}\theta }}{{2\pi }}\frac{{\pi \nu D^2}}{{\hbar \rho s^2}}2T,$$ (10) Then the transport scattering rate equals

$${\mathrm{\Gamma}}_{{\mathrm{tr}}} = {\oint} {\mathrm{d}}\Gamma\,(1 - {\mathrm{cos}}\theta ) = \frac{{2\pi \nu D^2{\mathrm{T}}}}{{\hbar \rho s^2}}{\oint} \frac{{\mathrm{d}\theta }}{{2\pi

}}{\mathrm{cos}}^2(\theta )(1 - {\mathrm{cos}}\theta ) = \frac{{\pi \nu D^2{\mathrm{T}}}}{{\hbar \rho s^2}}.$$ (11) The electron–phonon mean free path is given by _l_el−ph = _v_/Γtr, where

_v_ = ℏ_k__F_/_m_* is the carrier velocity. For bilayer graphene, we assume surface mass density _ρ_ = 2 × 7.6 × 10−7 kg/m2, the speed of sound _s_ = 2 × 104m/s. In single-layer graphene,

transport measurements are consistent with deformation potential _D_ of the order of 20 eV, see, e.g., ref. 41. For bilayer graphene, ab-initio calculations42 yield _D_ = 15 eV. Assuming _D_

in the range of 15–20 eV, we arrive at _l_el−ph of the order of 3 μm for typical experimental conditions. Table 1 provides a summary of the results for the single-layer and bilayer

graphene. These estimates are in agreement with the el-ph scattering rates extracted from the temperature dependence of the four-probe resistance reported in the ref. 16. DETAILS OF THE

THEORETICAL MODEL To describe the ballistic and viscous regimes on equal footing and provide a link between them, we use the kinetic Boltzmann equation for quasiparticles at the Fermi

surface. Expanded to linear order in the deviation _δf_ from the equilibrium Fermi-Dirac distribution, Boltzmann equation reads $$v\nabla _x\delta f(p,x) - I_{ee}(\delta f(p,x)) = J(p,x).$$

(12) The collision operator _I_ee in (12) describes scattering between single-particle states via momentum-conserving ee collisions. Near the Fermi surface, the distribution can be

parameterized by the standard ansatz \(\delta f(p) = - \frac{{\partial f_0}}{{\partial \varepsilon }}\chi (p)\), where the energy dependence in _χ_ can be ignored on the account of fast

quasiparticle thermalization by collinear scattering at the 2D Fermi surface32,33. We analyze the angular dependence _χ_(_θ_), where the angle _θ_ parameterizes the Fermi surface and \(\hat

p = ({\mathrm{cos}}\theta ,{\mathrm{sin}}\theta )\) is the unit vector along the carrier momentum. We assume that all non-conserved angular harmonics of _χ_(_θ_) relax with equal rates _γ_ee

 = _v_F/_l_ee,whereas the three angular harmonics corresponding to the conserved net momentum and particle number do not relax. The operator _I_ee, linearized in _χ_, therefore takes the

form13,22: $$I_{{\mathrm{ee}}}(\chi (\theta )) = - \gamma _{{\mathrm{ee}}}\left( {\chi (\theta ) - \langle \chi (\theta \prime )\rangle - 2\hat p \times \langle \hat p\prime \chi (\theta

\prime )\rangle } \right).$$ (13) The angular brackets denote angular averaging over _θ_′. To model the current flow in the strip geometry shown in Fig. 5, the Eq. (12) is to be furnished

with the boundary conditions describing momentum relaxation at the strip edges. We assume that particles are scattered diffusely, following Lambert’s law. Hence the edges _y_ = 0 and _y_ = 

_W_ effectively become isotropic current sources. At _y_ = 0, we write $$\chi (\theta > 0,x) = J(\theta ,x) + \frac{1}{2}\mathop {\int}\limits_0^\pi {\mathrm{sin}}\theta \prime \chi ( -

\theta \prime ,x){\mathrm{d}}\theta\prime .$$ (14) The choice of the coefficient 1/2 in the second term is dictated by current conservation. Indeed, for an isotropic distribution of outgoing

particles, _χ_(_θ_ > 0) = _χ_0, the outgoing particle flux, \(\nu \mathop {\int}\limits_0^\pi v_{\mathrm{F}}{\mathrm{sin}}\theta \chi (\theta ){\mathrm{d}}\theta /2\pi\), is given by

_νv_F_χ_0/_π_. Here _ν_ is the density of particle states, and _v_F is the Fermi velocity. In the absence of current injection, this quantity must be equal to the incoming flux which is

given by the integral in the second term. Similarly, an isotropic current source attached to the boundary, _I_(_x_, 0), is described via _J_(_θ_, _x_) = _πI_(_x_)/(_eνv_F) in the Eq. (14).

For the opposite orientation of the boundary, _y_ = _W_, positive and negative angle values in the Eq. (14) are to be interchanged. In general, distribution of particles in the Knudsen

regime is not represented by a local equilibrium Fermi function, and a local chemical potential cannot be introduced. This poses a difficulty in relating the signal on a probe contact to the

distribution function. To resolve this, we adopt the model of a probe which is commonly used to describe leads in mesoscopic circuits, see e.g.,43. A probe is a perfect absorber for

nonequilibrium carriers, which are equilibrated inside the probe and subsequently re-emitted into the fluid with an isotropic angular distribution. If the open-circuit condition is

maintained in the probing circuit, the potential on the probe is proportional to the influx _F_ of charge carriers into the probe, $$F = \nu \mathop {\int}\limits_0^{ - \pi } v_{\mathrm{F}}(

- {\mathrm{sin}}\theta )\chi (\theta ,x)\frac{{\mathrm{d}\theta }}{{2\pi }}.$$ (15) Since outgoing charge carriers are in equilibrium with the probe potential _V_p, they are characterized

by the distribution function _χ_ = _eV_p, so that the outgoing flux is _νeV_p/_π_. Balancing these fluxes, one finds the probe potential $$V_{\mathrm{p}}(x) = \frac{1}{{2e}}\mathop

{\int}\limits_0^\pi {\mathrm{sin}}\theta \chi ( - \theta ,x){\mathrm{d}}\theta.$$ (16) In the hydrodynamic regime, the distribution function is given by an equilibrium expression, which can

be related to the local electric potential, _χ_(_θ_, _x_) ≈ _eϕ_(_x_). In this limit, one finds _V_p(_x_) = _ϕ_(_x_). For a generic nonequilibrium distribution, however, the relation between

the local potential _ϕ_(_x_) and the probe signal _V_p(_x_) is less straightforward. In particular, in the ballistic limit (_l_ee = ∞) the probe attached to the edge of the sample does not

register particles grazing along the edge. This suppresses the space charge effect, however this suppression is not a universal phenomenon, and should be viewed as an approximation.

NUMERICAL MODELING To model the experimental geometry of Fig. 1a, we analyze the flow induced in a strip of width _W_, 0 < _y_ < _W_ by a point source on its edge at the point (0, 0)

and a drain at _x_ = −∞, see Fig. 4. Such a flow can be represented as a superposition of a symmetric flow emitted by the source with a uniform flow directed to the drain electrode. Both

flows can be analysed numerically via the approach described below. First, we pass to the Fourier representation with respect to the coordinate _x_ along the strip, and discretize the

transverse coordinate: _y__n_ = _nh_, where _h_ = _W_/_N__y_ is the step size, _n_ = 0,…, _N__y_ − 1. We also discretize the momentum direction as _θ__i_ = _π_(_i_ + 1/2)/_N__θ_, _i_ = 

0,…2_N__θ_ − 1. Hence the distribution function becomes a function of the wavevector _k_ and two discrete coordinates, $$\chi \left( {x,y = nh,\theta = \theta _i} \right) = {\int} \chi

_{n,i}(k)e^{ikx}\frac{{{\mathrm{d}}k}}{{2\pi }}.$$ (17) We employ the following finite-difference representation of the kinetic equation (13): $$\begin{array}{r}\frac{{{\mathrm{sin}}\theta

_i}}{h}\left[ {\chi _{n,i} - \chi _{n - 1,i}e^{ - ikh\,{\mathrm{cotan}}\theta _i}} \right] = I_{{\mathrm{ee}}}[\chi _{n,i\prime }],\\ \frac{{{\mathrm{sin}}\theta _i}}{h}\left[ {\chi _{n +

1,i}e^{ikh\,{\mathrm{cotan}}\theta _i} - \chi _{n,i}} \right] = I_{{\mathrm{ee}}}[\chi _{n,i\prime }].\end{array}$$ (18) For numerical stability, the scheme is made “upwind”: the form on the

first line should be applied for upward-going particles (0 < _θ__i_ < _π_), and the form on the second line describes particles propagating downwards. Due to the choice of the

exponential factors, the exact solution of (12) in the collisionless limit (_γ_ee = 0), \(\chi (k,y,\theta ) \propto {\mathrm{exp}}( - iky\,{\mathrm{cotan}}\theta )\), satisfies the

discretized equation. Thus, discretization of the advection term in Boltzmann equation, (_v_∇)_δf_, links the values of the distribution function at nearby sites. The discretized form of the

collision integral (13) mixes propagation angles within the same site. Therefore, the above finite-difference system, together with the boundary conditions (14) can be recast into the

well-known three-diagonal form in which only blocks on three adjacent sites _n_ and _n_ ± 1 are coupled: $$A_{n,ij}(k)\chi _{n - 1,j}(k) + B_{n,ij}\chi _{n,j}(k) + C_{n,ij}(k)\chi _{n + 1,j}

= b_{n,i}(k).$$ (19) Here _A__n_,_ij_(_k_), _B__n_,_ij_(_k_) and _C__n_,_ij_(_k_) are matrix operators acting on the angular index _i_ describing propagation of particles and scattering

between different momentum directions. The right-hand side _b__n_,_i_(_k_) describes external sources of particles. Such a system can be efficiently solved via the standard three-diagonal

matrix algorithm44. The point source was represented as a source term in the Eq. (14), with Fourier image _I_(_k_) = 1. The uniform Poiseuille-like flow can be obtained by analyzing the _k_ 

= 0 limit of the three-diagonal system (19), in which the flow is dragged by an external bias field. The bias field is incorporated into the Eq. (12) via the term −_eE_cos_θ_. The value of

the bias field _E_ is then obtained by normalizing the solution to the total current of 1/2. To make sure that the details of the boundary layer near the edges are simulated properly, we

have chosen a rather fine grid, _N__y_ = 5000. The propagation angles were discretized with _N__θ_ = 50, which corresponds to 3.6° step in _θ_. The particle distribution _χ__n_,_i_(_k_) was

calculated for |_k_|_W_ < 50, which gives a satisfactory approximation to the distances of interest, 0.1_W_ < _x_ < _W_. The probe signal was then calculated as the particle flux

(16), giving the results shown in Figs. 1c, 2b, 3b. DATA AVAILABILITY The datasets generated and/or analyzed during the current study are available from the corresponding author on

reasonable request. REFERENCES * Damle, K. & Sachdev, S. Nonzero-temperature transport near quantum critical points. _Phys. Rev. B_ 56, 8714–8733 (1997). Article  ADS  CAS  Google

Scholar  * Müller, M., Schmalian, J. & Fritz, L. Graphene: a nearly perfect fluid. _Phys. Rev. Lett._ 103, 025301 (2009). Article  ADS  Google Scholar  * Andreev, A. V., Kivelson, S. A.

& Spivak, B. Hydrodynamic description of transport in strongly correlated electron systems. _Phys. Rev. Lett._ 106, 256804 (2011). Article  ADS  CAS  Google Scholar  * Forcella, D.,

Zaanen, J., Valentinis, D. & van der Marel, D. Electromagnetic properties of viscous charged fluids. _Phys. Rev. B_ 90, 035143 (2014). Article  ADS  Google Scholar  * Tomadin, A.,

Vignale, G. & Polini, M. Corbino disk viscometer for 2D quantum electron liquids. _Phys. Rev. Lett._ 113, 235901 (2014). Article  ADS  Google Scholar  * Sheehy, D. E. & Schmalian, J.

Quantum critical scaling in graphene. _Phys. Rev. Lett._ 99, 226803 (2007). Article  ADS  Google Scholar  * Fritz, L., Schmalian, J., Müller, M. & Sachdev, S. Quantum critical transport

in clean graphene. _Phys. Rev. B_ 78, 085416 (2008). Article  ADS  Google Scholar  * Narozhny, B. N., Gornyi, I. V., Titov, M., Schütt, M. & Mirlin, A. D. Hydrodynamics in graphene:

Linear-response transport. _Phys. Rev. B_ 351, 035414 (2015). Article  ADS  Google Scholar  * Cortijo, A., Ferreirós, Y., Landsteiner, K. & Vozmediano, M. A. H. Hall viscosity from

elastic gauge fields in Dirac crystals. _Phys. Rev. Lett._ 115, 177202 (2015). Article  ADS  Google Scholar  * Gurzhi, R. N. Hydrodynamic effects in solids at low temperature. _Usp. Fiz.

Nauk_ 94, 689–718 (1968). Article  Google Scholar  * Gurzhi, R. N. Minimum of resistance in impurity-free conductors. _J. Exp. Theor. Phys._ 17, 521 (1963). Google Scholar  * Lifshitz, E. M.

& Pitaevskii, L. P. _Physical Kinetics_. (Pergamon Press, New York, 1981). Google Scholar  * de Jong, M. J. M. & Molenkamp, L. W. Hydrodynamic electron flow in high-mobility wires.

_Phys. Rev. B_ 51, 13389–13402 (1985). Article  Google Scholar  * Molenkamp, L. W. & de Jong, M. J. M. Observation of Knudsen and Gurzhi transport regimes in a two-dimensional wire.

_Solid State Electron_ 37, 551 (1994). Article  ADS  CAS  Google Scholar  * Jaggi, R. Electron-fluid model for the dc size effect. _J. Appl. Phys._ 69, 816–869 (1991). Article  ADS  CAS 

Google Scholar  * Bandurin, D. A. et al. Negative local resistance caused by viscous electron backflow in graphene. _Science_ 351, 1055–1058 (2016). Article  ADS  CAS  Google Scholar  *

Crossno, J. et al. Observation of the Dirac fluid and the breakdown of the Wiedemann-Franz law in graphene. _Science_ 351, 1058–1061 (2016). Article  ADS  CAS  Google Scholar  * Moll, P. J.

W., Kushwaha, P., Nandi, N., Schmidt, B. & Mackenzie, A. P. Evidence for hydrodynamic electron flow in PdCoO2. _Science_ 351, 1061–1064 (2016). Article  ADS  CAS  Google Scholar  *

Lucas, A., Crossno, J., Fong, K. C., Kim, P. & Sachdev, S. Transport in inhomogeneous quantum critical fluids and in the Dirac fluid in graphene. _Phys. Rev. B_ 93, 075426 (2016).

Article  ADS  Google Scholar  * Levitov, L. & Falkovich, G. Electron viscosity, current vortices and negative nonlocal resistance in graphene. _Nat. Phys._ 12, 672–676 (2016). Article 

CAS  Google Scholar  * Falkovich, G. & Levitov, L. Linking spatial distributions of potential and current in viscous electronics. _Phys. Rev. Lett._ 119, 066601 (2017). Article  ADS 

Google Scholar  * Guo, H., Ilseven, E., Falkovich, G. & Levitov, L. Higher-than-ballistic conduction of viscous electron flows. _Proc. Natl Acad. Sci._ 114, 3068–3073 (2017). Article 

ADS  CAS  Google Scholar  * Krishna Kumar, R. et al. Superballistic flow of viscous electron fluid through graphene constrictions. _Nat. Phys._ 13, 1182–1185 (2017). Article  CAS  Google

Scholar  * Pellegrino, F. M. D., Torre, I. & Polini, M. Nonlocal transport and the Hall viscosity of two-dimensional hydrodynamic electron liquids. _Phys. Rev. B_ 96, 195401 (2017).

Article  ADS  Google Scholar  * Berdyugin, A. I. et al. Measuring hall viscosity of Graphene’s electron fluid electron systems. http://arXiv:1806.01606 (2018). * Shytov, A., Kong, J. F.,

Falkovich, G. & Levitov, L. Electron collisions and negative nonlocal response of ballistic electrons. _Phys. Rev. Lett_. https://arXiv:1806.09538 (2018). * Wang, L. et al.

One-dimensional electrical contact to a two-dimensional material. _Science_ 342, 614–617 (2013). Article  ADS  CAS  Google Scholar  * Torre, I., Tomadin, A., Geim, A. K. & Polini, M.

Nonlocal transport and the hydrodynamic shear viscosity in graphene. _Phys. Rev. B_ 92, 165433 (2015). Article  ADS  Google Scholar  * Ho, D. Y. H., Yudhistira, I., Chakraborty, N. &

Adam, S. Theoretical determination of hydrodynamic window in monolayer and bilayer graphene from scattering rates. _Phys. Rev. B_ 97, 121404(R) (2018). Article  ADS  Google Scholar  *

Beconcini, M. et al. Scaling approach to tight-binding transport in realistic graphene devices: the case of transverse magnetic focusing. _Phys. Rev. B_ 94, 115441 (2016). Article  ADS 

Google Scholar  * Scaffidi, T., Nandi, N., Schmidt, B., Mackenzie, A. P. & Moore, J. E. Hydrodynamic electron flow and hall viscosity. _Phys. Rev. Lett._ 118, 226601 (2017). Article  ADS

  Google Scholar  * Chaplik, A. V. Energy spectrum and electron scattering processes in inversion layers. _Sov. Phys. JETP_ 33, 997 (1971). ADS  Google Scholar  * Giuliani, G. F. &

Quinn, J. J. Lifetime of a quasiparticle in a two-dimensional electron gas. _Phys. Rev. B_ 26, 4421 (1982). Article  ADS  CAS  Google Scholar  * Polini, M. & Vignale, G. The

quasiparticle lifetime in a doped graphene sheet. Preprint at _arXiv_ http://arXiv:1404.5728 (2014). * Ledwith, P. J., Guo, H., Shytov, A. V. & Levitov, L. S. Head-on collisions and

scale-dependent viscosity in two-dimensional electron systems. http://arXiv:1708.02376 (2017). * Kretinin, A. V. et al. Electronic properties of graphene encapsulated with different

two-dimensional atomic crystals. _Nano Lett._ 14, 3270–3276 (2014). Article  ADS  CAS  Google Scholar  * Ben Shalom, M. et al. Quantum oscillations of the critical current and high-field

superconducting proximity in ballistic graphene. _Nat. Phys._ 12, 318–322 (2015). Article  Google Scholar  * Stauber, T., Peres, N. M. R. & Guinea, F. Electronic transport in graphene: a

semiclassical approach including midgap states. _Phys. Rev. B_ 76, 205423 (2007). Article  ADS  Google Scholar  * Vasko, F. T. & Ryzhii, V. Voltage and temperature dependencies of

conductivity in gated graphene. _Phys. Rev. B_ 76, 233404 (2007). Article  ADS  Google Scholar  * Hwang, E. H. & Sarma, S. Das Acoustic phonon scattering limited carrier mobility in

two-dimensional extrinsic graphene. _Phys. Rev. B_ 77, 115449 (2008). Article  ADS  Google Scholar  * Efetov, D. K. & Kim, P. Controlling electron-phonon interactions in graphene at

ultrahigh carrier densities. _Phys. Rev. Lett._ 105, 256805 (2010). Article  ADS  Google Scholar  * Borysenko, K. M. et al. Electron-phonon interactions in bilayer graphene. _Phys. Rev. B_

83, 161402(R) (2011). Article  ADS  Google Scholar  * Beenakker, C. W. J. & van Houten, H. Quantum transport in semiconductor nanostructures. _Solid State Physics_ 44, 1 (1991). Article

  Google Scholar  * Press, W. H., Flannery, B. P., Teukolsky, S. A. & Vetterling, W. T. _Numerical Recipes in C, Section 2.4, 2nd edition_. (Cambridge University Press, New York, 1997).

Google Scholar  Download references ACKNOWLEDGEMENTS We gratefully acknowledge support from the Simons Center for Geometry and Physics where some of the research was performed. D.A.B. and

A.K.G. acknowledge the financial support from Marie Curie program SPINOGRAPH, Leverhulme Trust, the Graphene Flagship and the European Research Council. R.K.K. research was supported by

EPSRC Doctoral Prize fellowship. G.F. research was supported by the Minerva Foundation, ISF Grant 882 and the RSF Project 14-22-00259. L.L. acknowledges support of the Center for Integrated

Quantum Materials under NSF award DMR-1231319; and Army Research Office Grant W911NF-18-1-0116. AUTHOR INFORMATION Author notes * These authors contributed equally: Denis A. Bandurin, Andrey

V. Shytov. AUTHORS AND AFFILIATIONS * School of Physics, University of Manchester, Oxford Road, Manchester, M13 9PL, UK Denis A. Bandurin, Roshan Krishna Kumar, Alexey I. Berdyugin, Moshe

Ben Shalom, Irina V. Grigorieva & Andre K. Geim * School of Physics, University of Exeter, Stocker Road, Exeter, EX4 4QL, UK Andrey V. Shytov * Department of Physics, Massachusetts

Institute of Technology, 77 Massachusetts Ave, Cambridge, MA02139, USA Leonid S. Levitov * National Graphene Institute, University of Manchester, Manchester, M13 9PL, UK Roshan Krishna

Kumar, Moshe Ben Shalom & Andre K. Geim * Weizmann Institute of Science, Rehovot, Israel Gregory Falkovich * Novosibirsk State University, Novosibirsk, Russia, 630090 Gregory Falkovich

Authors * Denis A. Bandurin View author publications You can also search for this author inPubMed Google Scholar * Andrey V. Shytov View author publications You can also search for this

author inPubMed Google Scholar * Leonid S. Levitov View author publications You can also search for this author inPubMed Google Scholar * Roshan Krishna Kumar View author publications You

can also search for this author inPubMed Google Scholar * Alexey I. Berdyugin View author publications You can also search for this author inPubMed Google Scholar * Moshe Ben Shalom View

author publications You can also search for this author inPubMed Google Scholar * Irina V. Grigorieva View author publications You can also search for this author inPubMed Google Scholar *

Andre K. Geim View author publications You can also search for this author inPubMed Google Scholar * Gregory Falkovich View author publications You can also search for this author inPubMed 

Google Scholar CONTRIBUTIONS L.S.L., G.F., and A.K.G. designed and supervised the project. M.B.S. fabricated the devices. Transport measurements and data analysis were carried out by D.A.B.,

A.I.B. and R.K.K. Theory analysis was done by A.V.S., L.S.L., and G.F. The manuscript was written by A.V.S., D.A.B., L.S.L., A.K.G., and G.F. A.I.B. and I.V.G. provided experimental

support. All authors contributed to discussions. CORRESPONDING AUTHOR Correspondence to Gregory Falkovich. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests.

ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY

MATERIAL PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation,

distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and

indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to

the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will

need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE

CITE THIS ARTICLE Bandurin, D.A., Shytov, A.V., Levitov, L.S. _et al._ Fluidity onset in graphene. _Nat Commun_ 9, 4533 (2018). https://doi.org/10.1038/s41467-018-07004-4 Download citation *

Received: 19 June 2018 * Accepted: 05 October 2018 * Published: 31 October 2018 * DOI: https://doi.org/10.1038/s41467-018-07004-4 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative