Reader TTS

ABSTRACT Aftershock occurrence is characterized by scaling behaviors with quite universal exponents. At the same time, deviations from universality have been proposed as a tool to

discriminate aftershocks from foreshocks. Here we show that the change in rheological behavior of the crust, from velocity weakening to velocity strengthening, represents a viable mechanism

to explain statistical features of both aftershocks and foreshocks. More precisely, we present a model of the seismic fault described as a velocity weakening elastic layer coupled to a

velocity strengthening visco-elastic layer. We show that the statistical properties of aftershocks in instrumental catalogs are recovered at a quantitative level, quite independently of the

value of model parameters. We also find that large earthquakes are often anticipated by a preparatory phase characterized by the occurrence of foreshocks. Their magnitude distribution is

significantly flatter than the aftershock one, in agreement with recent results for forecasting tools based on foreshocks. SIMILAR CONTENT BEING VIEWED BY OTHERS THE IMPACT OF FAULTING

COMPLEXITY AND TYPE ON EARTHQUAKE RUPTURE DYNAMICS Article Open access 30 October 2022 AFTERSHOCKS ARE FLUID-DRIVEN AND DECAY RATES CONTROLLED BY PERMEABILITY DYNAMICS Article Open access 13

November 2020 RECURRENCE TIME AND SIZE OF CHILEAN EARTHQUAKES INFLUENCED BY GEOLOGICAL STRUCTURE Article 15 December 2023 INTRODUCTION Earthquakes occur in brittle regions of the crust

characterized by a velocity-weakening friction, which is at the origin of the stick-slip behavior. The distribution of friction along the fault plane is highly heterogeneous with strong

spots, usually called asperities1. Asperities are expected to be surrounded by weak zones with a rheological behavior better described by a velocity-strengthening friction. When the stress

accumulated in the surroundings of the hypocenter overcomes the local friction, an abrupt slip takes place and stress is redistributed in the surrounding regions. The stress redistribution

along the brittle, velocity-weakening, part of the crust triggers the occurrence of other earthquakes, the aftershocks. They follow well established empirical laws that can be put in the

form of power laws with quite universal values for the exponents2. In particular, the aftershock rate exhibits a roughly hyperbolic decay with time since the mainshock, an empirical law

known as the Omori–Utsu law3. At the same time, the stress redistributed by the mainshock in velocity-strengthening regions induces some slow deformations, commonly defined as afterslip.

Under the hypothesis4,5 of proportionality between seismicity rate _λ_(_t_) and afterslip rate, several features of aftershock occurrence are reproduced4,5,6,7,8,9,10. In ref. 11, we have

demonstrated this proportionality in a model with only two elastically coupled degrees of freedom. The first described the fault displacement, with an heterogeneous velocity-weakening

friction, while the second corresponded to the ductile region displacement, with a velocity-strengthening friction. This very simple description can model different tectonic contexts and

suggests that the coupling with a velocity-strengthening layer and the heterogeneity in the fault friction are the two key ingredients controlling aftershock triggering. The same two

ingredients are central in the pre-slip hypothesis12,13,14 according to which small earthquakes, usually named foreshocks15,16, are expected to anticipate the mainshock occurrence. According

to this hypothesis, because of friction heterogeneity, there are small regions on the fault that have less resistive power than the large fault and can break before it, in presence of an

underlying slow-deformation process. This mechanism can produce an increase of the seismic activity, as the occurrence time of the mainshock is approaching but, because of the limited number

of foreshocks, it is very difficult to be identified17,18,19,20. Nevertheless, accurate investigations before some recent large earthquakes have elightened the presence of foreshocks

together with a phase of slow slip of the plate interface21,22,23. Other precursory patterns are observed if one considers the distribution in space of foreshocks24,25,26,27 and/or their

distribution in magnitude28,29,30,31. In particular, very recently, Gulia and Wiemer31 have shown that the magnitude distribution during aftershock activity is steeper than during foreshock

activity. This result is however achieved for only two mainshocks and by means of different selection criterions for the foreshock identification32. In this article, we show that friction

heterogeneities and the slow deformation of a velocity-strengthening layer are sufficient ingredients to explain the whole ensemble of instrumental findings regarding the organization in

time, space, and magnitude of both aftershocks and foreshocks. To this extent, we combine the model of two blocks of Lippiello et al.11 with the description of the fault plane originally

proposed by Burridge and Knopoff (BK)33: a two-dimensional elastic interface with many degrees of freedom, each being subject to a velocity-weakening friction law. Therefore our model of the

fault consists in a collection of sliding blocks connected to a more ductile region, itself treated as an extended interface subject to velocity-strengthening rheology. This system has a

clear geophysical justification and allows us to study the organization of simulated earthquakes not only over time but also in space and in magnitude. We find that the model reproduces the

most relevant empirical laws observed for instrumental aftershocks and foreshocks, quite independently of the precise value of model parameters. RESULTS AND DISCUSSION THE MODEL The model we

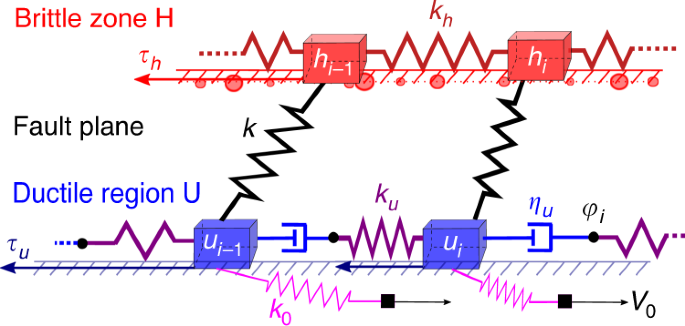
propose is composed by a first layer H that represents the brittle part of the fault. H is elastically coupled to a second layer U that mimics the ductile region below the fault and is

driven by the tectonic dynamics at the (very small) velocity _V_0. Each layer is an extended object made of many interacting degrees of freedom labeled _i_ = 1, 2, …, _N_, organized on a

square lattice. For simplicity, we assume a motion restricted along the _V_0 direction, with scalar displacements _h__i_(_t_) in the layer H and _u__i_(_t_) in the layer U. In Fig. 1, we

present a schematic description corresponding to a one-dimensional cut of the mechanical model along the _V_0 direction. The model also extends in the other direction, which is orthogonal to

_V_0. From continuum mechanics, the elastic cost of the displacement field is \({k}_{h}{\sum }_{j\ne i}({h}_{j}-{h}_{i})/{r}_{ij}^{2}\), where _r__i__j_ is the distance between points _i_

and _j_. The constitutive equations for the displacements _h__i_ in the layer H are obtained from the balance between the elastic forces and the velocity-weakening friction force _τ__h_:

$${\tau }_{h}={k}_{h}\sum_{j\ne i}\frac{{h}_{j}-{h}_{i}}{{r}_{ij}^{2}}+k({u}_{i}-{h}_{i}).$$ (1) To improve the efficiency of our numerical scheme, we restrict the sum in Eq. (1) to nearest

neighbors ∣_r__i__j_∣ = 1, which corresponds to replacing the elastic force with the discrete Laplacian _k__h_∇2_h__i_. The total stress on _i_ simplifies to _k__h_∇2_h__i_ + _k_(_u__i_ − 

_h__i_) (it is balanced by the friction _τ__h_). We also apply this short-range approximation to the layer U, which is, however, more ductile. For this reason, we assume that the

viscoelastic interactions34 in U are implemented assuming that neighboring degrees of freedom are connected by means of a dashpot and a spring placed in series (Fig. 1)35,36. The

constitutive equations for the layer U reads: $${\tau }_{{u}_{i}}={k}_{u}({\nabla }^{2}{u}_{i}-{z}_{i})+k({h}_{i}-{u}_{i})+{k}_{0}({V}_{0}t-{u}_{i})$$ (2) $$\eta \

{\dot{z}}_{i}={k}_{u}({\nabla }^{2}{u}_{i}-{z}_{i}),$$ (3) where _z__i_ is the viscoelastic degree of freedom, and the dot indicates a temporal derivative. The viscoelastic force

_k__u_(∇2_u__i_ − _z__i_) has an intrinsic timescale _t__η_ = _η_/_k__u_. When _u__i_ moves, for times shorter than _t__η_ the dashpot variable _z__i_ remains frozen, so the term

_k__u_(∇2_u__i_ − _z__i_) acts as a genuine elastic stress, and the layer U is solid-like. At longer times, the variable _z__i_(_t_) evolves to suppress the viscoelastic force (_z__i_ = 

∇2_u__i_), and the layer U displays a liquid-like behavior. Finally, we have to define the form of the friction forces. For the force _τ__u_ of the ductile layer U, we assume a

velocity-strengthening friction, taking the stationary form of the rate-and-state friction (RSF) law37,38,39: $${\tau }_{u}(t)={\sigma }_{N}\left({\mu }_{c}+A\,

{\mathrm{log}}\,\frac{{\dot{u}}_{i}(t)}{{V}_{c}}\right),$$ (4) where _σ__N_ is the effective normal stress, _μ__c_ is the friction coefficient when the block _U_ slides at the steady

velocity _V__c_ and _A_ > 0 for a velocity-strengthening material. For the friction in the brittle fault _H_, a random Coulomb failure criterion is adopted. As soon as the force overcomes

a local random frictional stress threshold \({\tau }_{i}^{\mathrm{{th}}}\), the position _h__i_ becomes unstable and moves forward by a random amount (Δ_h_)_i_. Slips of this kind are the

bulk of earthquakes and occur on the very fast timescale _t__s_, typically of the order of seconds. It is reasonable to assume that _t__s_ is the shortest timescale in the problem, and by

far, _t__s_ ≪ _t__η_, i.e., we assume it is instantaneous. Thus during an earthquake the layer _U_ behaves elastically and Eq. (2) can be approximated by $${\tau }_{{u}_{i}}={k}_{u}{\nabla

}^{2}{u}_{i}+k({h}_{i}-{u}_{i})+{k}_{0}({V}_{0}t-{u}_{i})\qquad t \sim {t}_{s}\ll {t}_{\eta },$$ (5) the term _k__u__z__i_ being constant at these timescales, it plays no role in the

dynamics of _τ__u_, _u__i_. As a consequence, for each slip (Δ_h_)_i_ at position _i_ in _H_, there are slips \({(\Delta u)}_{j}={q}_{{r}_{ij}}{(\Delta h)}_{i}\) at all positions _j_ in the

layer U, where \({q}_{{r}_{ij}}\) is a decreasing function of the distance _r__i__j_. In general, the precise form of the \({q}_{{r}_{ij}}\) depends on the details of the dynamics of

_h__i_(_t_), _z__i_(_t_), 0 < _t_ < _t__s_ and can be quite complicated. Indeed, when we apply the RSF laws combined with all other equations (Eq. (3) in particular) to compute the

true form of \({q}_{{r}_{ij}}\), we find a very fast decay as a function of _r__i__j_, and thus decide to neglect terms that are not nearest neighbor to the slipping site. Thus in practice

we use a short-range form for \({q}_{{r}_{ij}}\): \({q}_{{r}_{ii}}={q}_{0}\), \({q}_{{r}_{ij}}={q}_{1}\), if ∣_r__i__j_∣ = 1 and 0 for all others. After the earthquake, at times _t_ > 

_t__η_, the dashpots of the layer U are relaxed and have dissipated some elastic stress (the _k__u_∇2_u__i_ term is exactly compensated by  −_k__u__z__i_). In this phase the _u__i_’s are

decoupled \((\eta {\dot{z}}_{i}=0)\) and Eq. (2) becomes $${\tau }_{u}(t)=k({h}_{i}-{u}_{i})+{k}_{0}({V}_{0}t-{u}_{i}),\quad t\,> \, {t}_{\eta }.$$ (6) Implementing the

velocity-strengthening friction (Eq. (4)), Eq. (6) admits an explicit solution4,11. More precisely, the time \({t}_{R}=\frac{A{\sigma }_{N}}{{k}_{0}{V}_{0}}\) represents the long timescale

associated with the afterslip of the layer U, and for _t__η_ < _t_ < _t__R_ one obtains $${u}_{i}(t)={u}_{i}({t}_{0})+{\rho }_{0}

\,{\mathrm{log}}\,\left(1+D\frac{t-{t}_{0}}{{t}_{R}}\right),$$ (7) where \({\rho }_{0}=\frac{A{\sigma }_{N}}{k+{k}_{0}}\) is a characteristic length and _D_ is a constant. Conversely, at

later times _t_ > _t__R_, the logarithmic motion becomes linear _u__i_(_t_) ~ _V__c__t_ with \({V}_{c}=\frac{{k}_{0}}{k+{k}_{0}}{V}_{0}\). To summarize, there are four timescales: (1) The

slip timescale _t__s_, which characterizes the duration of a single earthquake, (2) _t__η_ related to the viscoelastic response in the layer _U_, (3) _t__R_ which corresponds to the

posteismic phase, and (4) the inter-sequence timescale _t__d_ ~Δ_h_/_V__c_ which corresponds to the typical waiting time between consecutive seismic sequences. We assume an infinite time

separation (_t__s_ ≪ _t__R_ ≪ _t__d_), which is a realistic approximation for geophysical parameters together with _t__s_ ≪ _t__η_ < _t__R_. Under this hypothesis, three distinct phases

are identified: coseismic phase (_t_ ~ _t__s_ ≪ _t__η_), post-seismic phase _t_ ~ _t__R_, (_t__s_ ≪ _t_ ≪ _t__d_) and interseismic phase _t_ ~ _t__d_ ≫ _t__R_. Furthermore assuming that the

local displacement Δ_h_ is a constant independent of the position _i_, the temporal evolution of the model can be numerically implemented via a cellular automaton, for which each slip is

infinitely fast. In this approximation, the dynamics of the layer _H_ at location _i_ is completely characterized by the two contributions to the stress acting on that site, namely the

intra-layer stress _f__i_(_t_) = _k__h_∇2_h__i_ and the inter-layer stress _g__i_ = _k_(_u__i_ − _h__i_). The sum _f__i_ + _g__i_ is thus the total stress acting on block _i_. The details of

the evolution of the variables _f__i_ and _g__i_ are given in the “Methods” section. In general, when \({f}_{i}+{g}_{i}\ge {\tau }_{i}^{\mathrm{{th}}}\), there is a slip in the site _i_ and

the stress evolves at _i_ and at nearest-neighboring sites _j_: $${f}_{i}(t)\, \to \,{f}_{i}(t)-4\Delta f\\ {f}_{j}(t)\, \to \,{f}_{j}(t)+\Delta f\\ {g}_{i}(t)\, \to

\,{g}_{i}(t)-4{k}_{h}\Theta \Delta h\\ {g}_{j}(t)\, \to \,{g}_{j}(t)+\left(\Theta -\epsilon \right)\Delta f$$ (8) with \(\Delta f={k}_{h}\Delta h,\Theta =(1-{q}_{0})\frac{k}{4{k}_{h}}\) and

\(\epsilon =(1-{q}_{0}-4{q}_{1})\frac{k}{4{k}_{h}}\). The stress drop Δ_f_ is extracted from a Gaussian distribution with average value 〈Δ_f_〉 and standard deviation _σ_. During the

coseismic phase, the stress evolution is driven by all the slips in layer _H_. Conversely, during the post-seismic phase, the stress evolution is driven by the ductile behavior of the layer

_U_. More precisely, since _u__i_ evolves according to Eq. (7), one has _g__i_(_t_) = _g__i_(_t_0)_Φ_(_t_ − _t_0), where _Φ_(_t_) is a logarithmic decreasing function of time. During the

interseismic phase, the stress _g__i_(_t_) grows linearly in time at the very slow tectonic rate _k_0_V__c_. Since the specific value of 〈Δ_f_〉 is not relevant, we set 〈Δ_f_〉 = 1 and the

model presents only three parameters: _σ_, _Θ_, and _ϵ_. The standard deviation _σ_ quantifies the level of friction heterogeneity, whereas _Θ_ quantifies the elastic interaction between the

two layers, and in the limiting case _Θ_ = 0 the layer H is decoupled from the layer U. Finally, the parameter \(\epsilon \propto 1-{\sum }_{j}{q}_{{r}_{ij}}=1-{q}_{0}-4{q}_{1}\) controls

the amount of dissipation. In absence of friction in the layer _U_ (_τ__u_ = 0) and neglecting _k_0 from Eq. (5), mechanical equilibrium imposes \({\sum }_{j}{q}_{{r}_{ij}}=1\). However in

general, for a finite _k_0 and taking into account the inelastic deformations in the _U_ layer (the _z__i_ dynamics), \(\mathop{\sum }\nolimits_{j = 1}^{N}{q}_{{r}_{ij}}<1\). Accordingly,

_ϵ_ controls the value of an upper magnitude cutoff _m__U_ ≃ −1.5 log10 _ϵ_ (see Supplementary Fig. 3). In the main text, we present results for a fixed value of _ϵ_ = 0.008 which allows us

to explore a sufficiently large magnitude range without finite-size effects. The role of _ϵ_ and of the system size _L_ is explicitly investigated in Supplementary Figures. FUNDAMENTAL

QUANTITIES AND THEIR STATISTICAL FEATURES IN INSTRUMENTAL CATALOGS A key quantity is the seismic moment \({M}_{0}=A\overline{D}\), where _A_ is the fractured area and \(\overline{D}\) is the

average displacement. In spring-block models, _A_ corresponds to the number of blocks which have slipped at least once during the earthquake and _M_0 = ∑_i__n__i__Δ__h_, where _n__i_ is the

number of slips performed by the _i_th block during the earthquake. We next introduce the moment magnitude \(m=(2/3)\,{\mathrm{log}}_{10} \, {M}_{0}\). In instrumental catalogs, _m_ is

distributed according to the Gutenberg–Richter (GR) law: _P_(_m_) ~ 10−_b__m_, with quite a universal value40 of _b_ ≃ 1. It is worth noticing that the GR law corresponds to a power-law

decay of the distribution of the seismic moment \(P({M}_{0}) \sim {M}_{0}^{-1-2b/3}\). Furthermore, _M_0 is related to the fractured area _A_ by the scaling relation _M_0 ~ _A_3/2 equivalent

to the proportionality between _m_ and the logarithm of _A_, \(m={\gamma }_{0}\, {\mathrm{log}}_{10}\,A+{\rm{cnst}}\), with quite a universal coefficient _γ_0 = 141,42. COMPARISON WITH

PREVIOUS SPRING-BLOCK MODELS The description of a seismic fault in terms of spring and blocks was originally proposed by Burridge and Knopoff (BK)33. Bak and Tang43 have enlightened the

similarity between the BK model and the evolution of a simple cellular automaton model, the BTW model44. In the BTW model, the stress of each block increases in time with a constant rate

\(\dot{f}\), which models the tectonic loading, and when it reaches a uniform threshold _f_th, an earthquake starts by distributing stress to surrounding blocks. In the limit \(\dot{f}\to

0\), once the bond network is assigned the BTW model does not have tunable parameters, and is usually considered the paradigmatic example of self-organized system, since it spontaneously

evolves toward a state where the size of avalanches is power-law distributed. Identifying an avalanche with an earthquake, since the earthquake size is proportional to _M_0, self-organized

criticality provides a theoretical explanation for the GR law even, if it gives a too small, non-realistic value of _b_. Olami, Feder, and Christensen (OFC model)45 have subsequently shown

that, keeping the limit \(\dot{f}\to 0\), the BK model can be exactly mapped in a cellular automaton. The model we present coincides with the OFC model in the limit cases _Θ_ = 0 and _σ_ = 0

and, in turn, the OFC model coincides with the BTW model when _ϵ_ = 0. Interestingly, the OFC model presents an intermediate range of _ϵ_ values such that _M_0 is power-law distributed with

a _b_ value close to one. On the other hand, for any finite value of _ϵ_, in the OFC model _M_0 ∝ _A_ leading to _γ_0 = 2/3 for the coefficient of the _m_ − log _A_ scaling, different from

_γ_0 ≃ 1 of instrumental catalogs. Many modifications of the original OFC model have been proposed in the literature2,46, and we group them into three classes: (i) those introducing a second

timescale besides \(\dot{f}\); (ii) those introducing heterogeneity in the friction thresholds _f_th; (iii) those introducing both a second timescale and friction heterogeneity. A second

timescale is usually implemented in order to reproduce the temporal decay of the aftershock number which, indeed, can be attributed to a variety of time-dependent stress transfer

mechanisms47. Major examples of class I models are those implementing a viscous relaxation48,49,50,51 or a reductions in fault friction by means of RSF laws50. Concerning class II, the

relevance of frictional heterogeneities in earthquake triggering has been deeply investigated52 and, in particular, the OFC model with a random _f_th corresponds to the quenched

Edwards–Wilkinson (qEW) model35,36,53. This is a typical model for driven elastic interfaces in a random media and, in this case, it is well established that the seismic moment is power-law

distributed with _b_ independently of the value of _ϵ_2. Nevertheless, statistical patterns of seismic occurrence are better reproduced by class III models as shown in refs.

36,50,54,55,56,57,58,59,60,61,62. According to the value of the parameters _Θ_ and _σ_, our model can belong to the different classes. In particular, our conjecture is that class III models,

and in particular the model we present with finite values of _Θ_ > 0 and _σ_ > 0, belongs to the same universality class of seismic occurrence. This conjecture is supported by the

results of the subsequent section. In particular, we observe that for finite values of _Θ_ and _σ_ our model is very similar to the Viscoelastic quenched Edwards–Wilkinson (VqEW) model

introduced by Jagla et al.35. The key difference lies in the functional form of _Φ_(_t_). Indeed in our model, the use of a realistic velocity-strengthening rheology induces a logarithmic

variation of _Φ_(_t_) with time, which is the crucial ingredient leading to the Omori–Utsu hyperbolic decay of the aftershock rate. In the VqEW model instead, an exponential relaxation of

_Φ_(_t_) is obtained. THE MAGNITUDE DISTRIBUTION AND THE _M_ − LOG _A_ SCALING For each earthquake we record the occurrence time _t_, the hypocentral coordinates _i_ (i.e., the coordinate of

the block which nucleates the instability), the magnitude _m_, and the fractured area _A_. The simulated catalog contains about 107 earthquakes; however, we exclude the first 10% of events

so that results are independent of initial conditions. In the main text, we present results for different values of _Θ_ and _σ_, keeping _ϵ_ = 0.008 fixed. The results for different _ϵ_ are

discussed in the Supplementary Notes. The full separation of timescales allows us to clearly distinguish separate seismic sequences. We define a seismic sequence as the set of earthquakes

triggered by the relaxation of the layer U, according to Eq. (7), i.e., the set of earthquakes triggered during the post-seismic phase. A new sequence starts at much later times when an

earthquake is triggered during the interseismic phase with the slow stress rate increase _k_0_V__c_. Interestingly, as it is often observed in instrumental catalogs63, this first earthquake

in the sequence is not always the largest one. We adopt the convention used to classify events of real seismic sequences: the mainshock is the largest event in the sequence, the foreshocks

are all events occurring before it and the aftershocks are all the subsequent ones. In Fig. 2a, we plot an excerpt of the whole catalog. The lag time between two consecutive sequences

depends on the specific value of _t__d_. Before studying the features of aftershocks and foreshocks, we investigate the behavior of the global catalog. In Fig. 3, we plot the magnitude

distribution _P_(_m_) for different values of _Θ_ and _σ_. In particular, the OFC model45 (corresponding to _Θ_ = _σ_ = 0) gives an exponential decay with _b_ = 0.12 ± 0.02 up to a system

size-dependent upper cutoff _m__U_, whereas for the qEW model (_Θ_ = 0, _σ_ > 0), we find _b_ = 0.40 ± 0.02 independently of _ϵ_, with _m__U_ controlled by _ϵ_. Surprisingly, even for

small values of _Θ_, the presence of the velocity-strengthening layer U induces a dramatic and robust change in the _b_ value. For _Θ_ ≥ 0.1, in very good agreement with instrumental

catalogs, we always observe _b_ = 1.06 ± 0.05 for intermediate magnitudes ranging from a lower cutoff _m__L_ related to lattice-specific details, up to an upper cutoff _m__U_. Keeping _Θ_ 

> 0.1 fixed we also find that the result _b_ = 1.06 is independent of _σ_ (inset of Fig. 3), except for the singular choice _σ_ = 0, where the magnitude distribution presents a

non-monotonic behavior (not shown). The parameters _Θ_ and _σ_ only affect the value of _m__U_, which increases with them (Fig. 3). In particular, _m__U_ tends to _m__L_ when (_Θ_, _σ_) are

very small, shrinking to zero the range where _b_ ≈ 1. We also note an initial exponential decay \(P(m) \sim 1{0}^{-{b^{\prime}} m}\) for small magnitudes (smaller than _m__L_), with

\(b^{\prime}\) monotonically increasing with _Θ_ from \(b^{\prime} =0.65\) for _Θ_ = 0.1 to \(b^{\prime} =1.42\), when _Θ_ = 1. In particular, we find an intermediate range of _Θ_ values

(_Θ_ ∈ [0.4, 0.6]), where \(b^{\prime} \simeq b\), i.e., for which the _b_ ≃ 1 regime extends down to small magnitudes. Realistic _b_ values of the GR law have already been found by Jagla et

al.58,59 in models of only one layer, but including viscoelastic couplings or aging effect in the static friction coefficients36,54,55,56,57,58,59,60,61,62, which in both cases results in

an effective additional degree of freedom per lattice site (all these models are spatially extended). The coupling (_Θ_ > 0) with the layer U also allows us to recover the linear relation

between _m_ and _l__o__g_(_A_). In the OFC model (and when _ϵ_ ≃ 0), a degree of freedom slips at most once by construction and therefore _M_0 ∝ _A_, _γ_0 = 2/3 (Fig. 4). For the qEW model,

the theory of depinning predicts _γ_0 = 2(1 + _ζ_/_d_)/3, with _d_ the dimension of the interface (here it coincides with the layer, _d_ = 2) and _ζ_ its roughness exponent. Here, we have

_d_ = 2 and _ζ_ ~ 0.75 (for long-range elasticity, _ζ_ = 0). This is consistent with the values measured: _γ_0 = 0.87 ± 0.02 (Fig. 4). When _Θ_ > 0 and _σ_ > 0, we find a change to

_γ_0 = 0.96 ± 0.03, independently of _Θ_ and _σ_ (Fig. 4). STATISTICAL FEATURES OF AFTERSHOCKS AND FORESHOCKS Let us now consider the properties of aftershocks and foreshocks. Results do not

depend on the specific values of _Θ_ and _σ_, thus we only present them for intermediate value of _Θ_ = 0.5 and for _σ_ = 5. With these parameters, the GR law is obeyed over a sufficienly

large magnitude range. The spatial organization of a typical fore-main-aftershock sequence is plotted in Fig. 2c, d, which presents the contour of the area fractured by a mainshock (here

_m__M_ = 5.1) and the contours of fracured area of the largest aftershocks and foreshocks (_m_ > 1.5). Figure 2d just indicates that the whole sequence is concentrated in a narrow region

of the fault plane close to the mainshock epicenter, while a zoom inside this region (Fig. 2c) provides details of the spatial organization of events. First of all we observe that most

aftershocks occur close to the border of the mainshock’s fractured area. This is consistent with the gap hypothesis according to which the increase of stress on the border of the fractured

area triggers the aftershocks, whereas the stress reduction inside the fractured region strongly reduces their occurrence probability. This scenario is strongly supported by recent

observations of the aftershock organization after big mainshocks64. The same analysis of Wetzler et al.64 for the distribution of the aftershock hypocentral distance, from the contour of the

mainshock fractured area, is presented in Supplementary Fig. 5. In our model also, foreshocks occur close to the border of the area that will be fractured by the mainshock. In order to be

more quantitative, we plot (inset of Fig. 5) the number of aftershocks _n_aft(_m__M_) and foreshocks \({n}_{{\rm{fore}}}({m}_{M})\) as a function of the mainshock magnitude. We find an

exponential behavior \({n}_{{\rm{aft}}}({m}_{M}) \sim 1{0}^{\alpha {m}_{M}}\), which is also observed in instrumental catalogs and known as the productivity law65,66. Also in this case we

find quantitative agreement with the value _α_ ≃ 1 observed in instrumental catalogs. The inset of Fig. 5 also shows an exponential behavior \({n}_{{\rm{fore}}}({m}_{M}) \sim 1{0}^{\alpha

{m}_{M}}\) for the foreshock number with _α_ ≃ 1, a result also observed in instrumental catalogs25,26. We also find that the number of foreshocks is usually ~100 times smaller than the

aftershock one, and we remark that only for the largest mainshock magnitude _m__M_, we do have a sufficient number of aftershocks (_n_aft(_m__M_) ≳ 1000) to study their statistical features

inside a single main-aftershock sequence. For this reason, to improve the statistics, we group sequences according to their mainshock’s magnitude, as it is usually done in instrumental

catalogs. More precisely, we consider the magnitude distribution of aftershocks (foreshocks) occurring after (before) a mainshock with magnitude _m_ ∈ (_m__M_, _m__M_ + 1]. Results (Fig. 5)

confirm that aftershock magnitudes are distributed according to the GR law with _b_ ≃ 1. Interestingly, we observe that also foreshocks follow the GR law but with a significantly smaller _b_

value _b_ ≃0.8. This result is consistent with the existence of an inverse relation between b value and local stress level, as indicated by many laboratory measurements and field

observations67,68,69. Accordingly, a smaller _b_ value (larger proportion of large earthquakes) is expected to be observed before the occurrence of the mainshock and close to its hypocenter,

as a signature of high stress conditions. Indeed, several studies report the decrease of the _b_ value while approaching the mainshock, and identifies it as a precursory pattern which can

improve mainshock forecasting28,29,30,31. Our study represents the first identification of this pattern in a mechanical model simultaneously presenting realistic features of aftershock

occurrence. We further note that our measure of the _b_ value is neither biased by the foreshock selection criterion (since we have a perfect separation of sequences) nor is it affected by

problems of magnitude completeness (we have access to the smallest earthquakes), which are typical of instrumental catalogs and can be responsible for spurious behaviors of the _b_ value. In

Fig. 6, we plot the number of aftershocks (foreshocks) _n_aft(_t_∣_m__M_) (_n_fore(_t_∣_m__M_)) as function of the time _t_ since (before) the mainshock with magnitude _m_ ∈ [_m__M_, _m__M_

 + 0.8), divided by the total number of mainshocks with _m_ ∈ [_m__M_, _m__M_ + 0.8). We find that the aftershock organization in time follows the Omori–Utsu law _n_aft(_t_) ~ _t_−_p_ with

_p_ = 1 over several decades. The inverse Omori law70,71 \({n}_{{\rm{fore}}}(t) \sim {t}^{-p}\), with _p_ = 1, is also found to characterize the temporal organization of foreshocks. It is

worth noticing that, at variance with the aftershock occurrence, a clear temporal behavior cannot be extracted from a single foreshock sequence because of the very small number of foreshocks

(we find at most 32 foreshocks during one sequence). Thus the inverse Omori law is only observed after stacking many sequences. The vertical shift of curves for different mainshock

magnitudes is consistent with the productivity law, in agreement with the inset of Fig. 5. At short times, there is an abrupt transition from an about flat behavior to the 1/_t_ decay. We

expect that assuming a finite ratio _t__η_/_t__R_ would smooth this transition and help better reproduce instrumental observations. In Fig. 7, we plot the density of aftershocks or

foreshocks _ρ_(_δ__r_, _m__M_) as a function of the distance _δ__r_ between their hypocenter and their mainshock’s hypocenter, grouping events by intervals of mainshock magnitude _m__M_ ∈

[_m__M_, _m__M_ + 0.8). There is a clear dependence on _m__M_, and at the same time for any _m__M_ the aftershocks and foreshocks share very similar spatial distributions, in agreement with

instrumental findings24,25,27. Foreshocks occur mostly over the area fractured by the mainshock, supporting the idea that their spatial organization contains information on the size of the

incoming mainshock (in that given region)24,25. Concretely, we find that _ρ_(_δ__r_, _m__M_) obeys the scaling law \(\rho (\delta r,{m}_{M})=L({m}_{M}) Q\left(\frac{\delta

r}{L({m}_{M})}\right)\) with \(L({M}_{m}) \sim 1{0}^{\gamma {m}_{M}}\) and _γ_ ≃ 0.57 ± 0.05. Similar collapses are observed in instrumental catalogs24,25,72,73,74, although a smaller value

_γ_ ≃ 0.5 is usually observed. A second difference lies in the decay of the scaling function _Q_(_δ__r_): in our model, it is exponential while power-law tails are reported in instrumental

catalogs74. This overly fast decay can be attributed to our approximate modeling of elastic interactions within each layer, the correct long-range interaction expected from elasto-static

theory2 being replaced (see Eq. (1)) with the short-range term _k__h_∇2_h__i_. Indeed under this short-range approximation, aftershocks can be triggered only within or at the boundary of the

rupture zone, as was shown in refs. 35,36. Finally, we note that this spatial clustering law can be related to the m–logA scaling of Fig. 4, with _γ_ = 1/(2_γ_0). Indeed since aftershocks

are mostly distributed on the border of the area fractured by the mainshock, one has \(L({m}_{M}) \sim \sqrt{A} \sim \sqrt{1{0}^{{m}_{M}/{\gamma }_{0}}} \sim 1{0}^{{m}_{M}\gamma }\).

APPLICATIONS AND IMPROVEMENTS We have implemented a minimal model for earthquake triggering, modeling the interaction between the brittle part of the crust (an elastic and velocity-weakening

region) and the ductile zone (a viscoelastic region with velocity-strengthening rheology). We assume short-range elasticity and infinite time separation, which allows to develop a cellular

automaton model controlled by only two parameters, _Θ_ and _σ_. Very interestingly, we find that as soon as _Θ_ and _σ_ are sufficiently different from zero, we recover the established

statistical features of aftershock occurrence, with realistic values of the parameters _b_, _α_, _γ_, _p_. This robustness strongly suggests that our model captures the universality class of

instrumental earthquakes. Our model thus provides useful insights on the mechanisms of aftershock triggering. For example, a deviation from the stationary behavior of the _b_ value is found

during foreshock sequences, supporting its interpretation as a precursory pattern for the mainshock occurrence. Although our model misses some features of instrumental earthquakes, such as

the power-law decay of the spatial density _ρ_, it can be very useful. Thanks to its simplicity, we can easily produce very complete synthetic catalogs to test forecasting hypothesis, or

mechanisms of stress evolution and how it is related to foreshocks, mainshocks, or aftershocks. It is also possible to extend the single-fault model presented in this study to a more

realistic description as a network of faults. One could then study the interaction between different branches of the network. METHODS DERIVATION OF THE CELLULAR AUTOMATON RULES We consider

two square layers of sides _L_ = 1000. In our lattice geometry, there are exactly four neighbors _j_ for each site _i_: the stress diffusion terms of the type \({({\nabla }^{2}h)}_{i}\) at

site _i_ with positions _x_, _y_ thus stand for \({({\nabla }^{2}h)}_{x,y}=({h}_{x+1,y}+{h}_{x-1,y}+{h}_{x,y+1}+{h}_{x,y-1}-4{h}_{x,y})\). We use absorbing boundary conditions (_h_ = 0 is

fixed at the boundary), which means that some stress is absorbed at the boundaries, and the slip cannot propagate further. We now recall the main assumptions of our continuous model, before

explicitly deriving the corresponding cellular automaton. These assumptions are summarized in the mechanical sketch of Fig. 1, from which the equations can be derived. The stress at site _i_

in the layer _H_ is the sum of intra-layer and inter-layer stresses, respectively: $${f}_{i}={k}_{h}{\nabla }^{2}{h}_{i}$$ (9) $${g}_{i}=k({u}_{i}-{h}_{i}).$$ (10) The total stress _f__i_ +

 _g__i_ at site _i_ is balanced by a velocity-weakening (Coulomb failure style) friction force _τ__h_, which takes a new random value, denoted \({\tau }_{i}^{\mathrm{{th}}}\), after each

slip: $${\tau }_{h}={\tau }_{i}^{\mathrm{{th}}} \sim G(\tau ) \sim {\mathcal{N}}(1,\sigma )$$ (11) where _G_(_τ_) is a gaussian distribution with average 1 and standard deviation _σ_. As

long as _τ__h_ ≥ _f__i_ + _g__i_ the site _i_ is pinned, that is \({\dot{h}}_{i}=0\). The constitutive equations operate on various timescales: $${\tau }_{h}\,\ge\, {f}_{i}+{g}_{i}\qquad

\,{{\text{slip}}\, {\text{timescale}}}\,\,{t}_{s}$$ (12) $${\tau }_{{u}_{i}}={k}_{u}({\nabla }^{2}{u}_{i}-{z}_{i})+k({h}_{i}-{u}_{i})+{k}_{0}({V}_{0}t-{u}_{i})\qquad \,{{\text{slip}}\,

{\text{timescale}}}\,\,{t}_{s}$$ (13) $$\eta \ {\dot{z}}_{i}={k}_{u}({\nabla }^{2}{u}_{i}-{z}_{i}),\qquad \,{\text{visco}}{\hbox{-}}{\text{elastic}} \, {\text{timescale}}\,\,{t}_{\eta

}=\frac{\eta }{{k}_{u}}$$ (14) $${\tau }_{{u}_{i}}(t)={\sigma }_{N}\left({\mu }_{c}+A\, {\mathrm{log}}\,\frac{{\dot{u}}_{i}(t)}{{V}_{c}}\right),\qquad \,{\text{relaxation}} \,

{\text{timescale}}\,\,{t}_{R}=\frac{{\rho }_{0}}{{V}_{c}}=\frac{A{\sigma }_{N}}{{k}_{0}{V}_{0}}$$ (15) The first two equations are the force balance between applied stresses and local

friction force, and are thus instantaneous. The third is the internal stress dynamics of the viscoelastic layer _U_, evolving over an intermediate timescale _t__η_. The fourth is the time

evolution of the velocity-strengthening friction, slowly evolving over a timescale _t__R_. We recall the constants: \({V}_{c}=\frac{{k}_{0}}{k+{k}_{0}}{V}_{0}\), \({\rho }_{0}=\frac{A{\sigma

}_{N}}{k+{k}_{0}}\). _-_ Initialization: At time _t_ = 0, we assign a local frictional threshold \({\tau }_{i}^{\mathrm{{th}}}\) extracted from _G_(_τ_). We also choose the initial value

_f__i_(0) of the local stress at random in the interval \((0,{\tau }_{i}^{\mathrm{{th}}})\) and suppose that at _u__i_(0) = _h__i_(0) in all sites. _-_ Interseismic phase: At time scales

larger than _t__s_, _t__η_, _t__R_, we have \({\dot{u}}_{i}={V}_{c}\) and the equations above simplify. Using Eq. (15), we get _τ__u_ = _μ__c_. At these long timescales (_t_ ≫ _t__η_), we

have \(\eta {\dot{z}}_{i}=0\) so that using Eq. (14), _z__i_ = ∇2_u__i_. Using Eq. (13), this combines to yield _k_0_V_0_t_ = (_k_ + _k_0)_V__c__t_, which explains the necessary definition

\({V}_{c}=\frac{{k}_{0}{V}_{0}}{k+{k}_{0}}\). We finally have _f__i_ + _g__i_ = const. + _k__V__c__t_, and using Eq. (12), we can compute the distance to failure (time before failure):

$${t}_{i}^{({\mathrm{drive}})}=\frac{{\tau }_{i}^{\mathrm{{th}}}-{f}_{i}({t}_{0})-{g}_{i}({t}_{0})}{k{V}_{c}}$$ (16) with _t_0 the time at the beginning of this phase. The site _i_*

corresponding to the smallest value of \({t}_{i}^{{\mathrm{(drive)}}}\) is thus identified as the hypocenter of the next earthquake. An amount of stress \({\tau }_{{i}^{*

}}^{\mathrm{{th}}}-{f}_{{i}^{* }}({t}_{0})-{g}_{{i}^{* }}({t}_{0})\) is then added to all sites and the coseismic phase is entered, with exactly one site being unstable (the one where

\({f}_{{i}^{* }}(t)+{g}_{{i}^{* }}(t)={\tau }_{{i}^{* }}^{\mathrm{{th}}}\)). _-_ Coseismic phase: Each site with \({f}_{i}(t)+{g}_{i}(t)\ge {\tau }_{i}^{\mathrm{{th}}}\) is unstable and

slips of a constant amount Δ_h_, _h__i_ → _h__i_ + Δ_h_. A slip in the layer _H_ at site _i_ induces a coseismic slip \({u}_{j}\to {u}_{j}+{q}_{{r}_{ij}}\Delta h\) inside the _U_ layer. As

explained in the main text, we set _q__r_ = 0 for _r_ > 1, i.e., we only keep the local coseismic slip \({q}_{{r}_{ii}}={q}_{0} \, > \,0\) and the nearest-neighbor coseismic slip

\({q}_{{r}_{ij}}={q}_{1} \,> \,0\) (when ∣_r__i__j_∣ = 1). Because of the ductile nature of the layer _U_ there is some dissipation occurring during the coseismic slip, in the sense that

the total coseismic slip is less than the slip: \(\overline{\epsilon }=1-{q}_{0}-4{q}_{1}\,> \,0\) (\(\overline{\epsilon }=0\) would be the dissipationless case). This coseismic slip is

considered instantaneous and corresponds to the following stress evolution, for the site _i_ itself and for its first neighbors _j_: $${f}_{i}(t)\to {f}_{i}(t)-4{k}_{h}\Delta h$$ (17)

$${f}_{j}(t)\to {f}_{j}(t)+{k}_{h}\Delta h$$ (18) $${g}_{i}(t)\to {g}_{i}(t)+k({q}_{0}-1)\Delta h$$ (19) $${g}_{j}(t)\to {g}_{j}(t)+k{q}_{1}\Delta h$$ (20) At this timescale, the internal

degrees of freedom _z__i_ are fixed and do not evolve. By introducing the parameters $$\Theta =(1-{q}_{0})\frac{k}{4{k}_{h}},$$ (21) $$\epsilon

=(1-{q}_{0}-4{q}_{1})\frac{k}{4{k}_{h}}=\overline{\epsilon }\frac{k}{4{k}_{h}},$$ (22) we can factorize: $${f}_{i}(t)\to {f}_{i}(t)-4{k}_{h}\Delta h$$ (23) $${f}_{j}(t)\to

{f}_{j}(t)+{k}_{h}\Delta h$$ (24) $${g}_{i}(t)\to {g}_{i}(t)-4{k}_{h}\Theta \Delta h$$ (25) $${g}_{j}(t)\to {g}_{j}(t)+\left(\Theta -\epsilon \right){k}_{h}\Delta h$$ (26) Which shows that

the coseismic slip stabilizes _g__i_ but increases the _g__j_ stresses. After a slip, the block _h__i_ is in a different frictional condition, i.e., a new value of \({\tau

}_{i}^{\mathrm{{th}}}\) is extracted from the distribution _G_(_τ_). If \({\tau }_{i}^{\mathrm{{th}}}\) is such that \({f}_{i}(t)+{g}_{i}(t)\,\ge\, {\tau }_{i}^{\mathrm{{th}}}\) then the

process of Eqs. (23)–(26) is iterated immediately, until \({f}_{i}(t)+{g}_{i}(t)\,<\, {\tau }_{i}^{\mathrm{{th}}}\). Because of the stress redistribution, nearest-neighbor sites _j_ can

be unstable and slip at the same time. In practice, we perform the updates of Eqs. (23)–(26) on all sites for which \({f}_{j}(t)+{g}_{j}(t)\ge {\tau }_{j}^{\mathrm{{th}}}\), until all sites

satisfy \({f}_{j}(t)+{g}_{j}(t)\,<\, {\tau }_{j}^{\mathrm{{th}}}\). We follow a sequential updating scheme, which implies the slip of just one unstable block at a time. Preliminary

results with an updating scheme where all unstable blocks simultaneously slip indicate no important difference. Shortly after the end of the earthquake, the viscoelastic couplings (internal

degrees of freedom _z__i_ of the layer _U_) relax their stress (over a timescale _t__η_ = _η_/_k__u_), which in practice means that \(\eta \dot{z}=0={k}_{u}({\nabla }^{2}{u}_{i}-{z}_{i})\).

As we explained in the main text, the way in which this relaxation affects the stress in the layer _U_ has already been included implicitly in the coslip dynamics, via the coefficients _q_0,

 _q_1, so that on longer timescales we can simply consider that _k__u_(∇2_u__i_ − _z__i_) = 0. In particular, Eq. (5) simplifies into Eq. (6), i.e., the blocks _u__i_ become independent. _-_

Post-seismic phase: At the end of an avalanche, the _h__i_ are stuck, so that the intra-layer stress _f__i_ remains constant. However, the _g__i_ may evolve. Indeed, the _u__i_ are subject

to a velocity-strengthening rheology and evolve according to Eq. (6), which can be integrated to give Eq. (7), that we recall here: \({u}_{i}(t)={u}_{i}({t}_{0})+{\rho }_{0}\,

{\mathrm{log}}\,\left(1+D\frac{t-{t}_{0}}{{t}_{R}}\right)\), where \(D=\exp \left(-g({t}_{0})/A{\sigma }_{N}\right)\) is a constant (over time, but different for each site). This solution

can be checked, using Eq. (15) on one side and Eq. (6) on the other. One may also consult our solution for the case of a two-blocks model11, which is the same since all sites _u__i_ evolve

independently during the afterslip (in the two-block model there was only one block _u_). Writing _g__i_(_t_) = _g__i_(_t_0) + _k_(_u__i_(_t_) − _u__i_(_t_0)), we can identify

$${g}_{i}(t)={g}_{i}({t}_{0})\Phi (t-{t}_{0})$$ (27) with $$\Phi (t-{t}_{0})=1-\frac{k}{k+{k}_{0}}\frac{{\mathrm{log}}\,\left(1+D\frac{t-{t}_{0}}{{t}_{R}}\right)}{{\mathrm{log}}\,(D)},$$

(28) and the local stress value evolves, at times _t_ ≥ _t_0, according to the equation: $${f}_{i}(t)+{g}_{i}(t)={f}_{i}({t}_{0})+{g}_{i}({t}_{0})(1-\Phi (t-{t}_{0})).$$ (29) We note that

this happens independently in all the sites (there is no stress transfer between sites, which makes the evolution very simple to compute). It is important to remark that _Φ_(_t_) is a

monotonically decreasing function of _t_. For _g__i_(_t_0) < 0 (which does happen), _D_ is large and at times _t_ − _t_0 ≫ _t__R_, _Φ_(_t_ − _t_0) ~ 0. Thus _Φ_ decreases from 1 to  ≈0.

This relaxation of the inter-layer stress _g__i_(_t_) happens to all sites simultaneously. If for a site _i_, \({f}_{i}({t}_{0})\,> \, {\tau }_{i}^{\mathrm{{th}}}\), there will be a time

_t_aft > _t_0 such that \({f}_{i}({t}_{{\mathrm{aft}}})+{g}_{i}({t}_{{\mathrm{aft}}})={\tau }_{i}^{\mathrm{{th}}}\). For some sites (depending on the slips dynamics), this condition is

not fulfilled and no such time exists. Computationally, we compute the time _t_aft for all sites where it is defined by inverting Eq. (29). Then we pick the smallest _t_aft, that we may call

\({t}_{{\mathrm{aft}}}^{* }\), and relax the stress in all sites according to Eq. (29) using \(t={t}_{{\mathrm{aft}}}^{* }\). At this point, there is thus exactly one site that became

unstable (the one with the smallest _t_aft), i.e., a new earthquake is triggered. We then proceed with the coseismic phase, until the earthquake is complete. This is the physical mechanism

which triggers aftershocks. After a number of aftershocks, there is a point where no site fulfills the condition \({f}_{i}({t}_{0})\,> \, {\tau }_{i}^{\mathrm{{th}}}\), i.e., no time

_t_aft can be defined. In that case, we perform relaxation “for infinite time” (several _O_(_t__R_)), or more concretely we set _g__i_ = 0 at all sites. At this point, the

fore-main-aftershock sequence is finished and the interseimic phase resumes, triggering a new sequence. DATA AVAILABILITY Numerical data that support the findings of this study are available

from the corresponding author upon reasonable request. CODE AVAILABILITY The source code of the numerical model is available from the corresponding author. REFERENCES * Lay, T. &

Kanamori, H. in _An Asperity Model of Large Earthquake Sequences_, Maurice Ewing Series, (eds Simpson D.W. & Richards P.G.) 579–592 (American Geophysical Union (AGU), 2013). * de

Arcangelis, L., Godano, C., Grasso, J. R. & Lippiello, E. Statistical physics approach to earthquake occurrence and forecasting. _Phys. Rep._ 628, 1–91 (2016). Article  ADS  MathSciNet 

Google Scholar  * Utsu, T., Ogata, Y. & Matsu’ura, S. R. The centenary of the Omori formula for a decay law of aftershock activity. _J. Phys. Earth_ 43, 1–33 (1995). Article  Google

Scholar  * Perfettini, H. & Avouac, J.-P. Postseismic relaxation driven by brittle creep: a possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks,

application to the Chi-Chi earthquake, Taiwan. _J. Geophys. Res.: Solid Earth_ 109, B02304 (2004). ADS  Google Scholar  * Perfettini, H. & Avouac, J. Modeling afterslip and aftershocks

following the 1992 Landers earthquake. _J. Geophys. Res.: Solid Earth_ 112, https://doi.org/10.1029/2006JB004399 (2007). * Perfettini, H., Avouac, J.-P. & Ruegg, J.-C. Geodetic

displacements and aftershocks following the 2001 Mw = 8.4 Peru earthquake: implications for the mechanics of the earthquake cycle along subduction zones. _J. Geophys. Res.: Solid_ _Earth_

110, https://doi.org/10.1029/2004JB003522 (2005). * Hsu, Y.-J. et al. Frictional afterslip following the 2005 Nias-Simeulue earthquake, Sumatra. _Science_ 312, 1921–1926 (2006). Article  ADS

  CAS  PubMed  Google Scholar  * Canitano, A. et al. Seismicity controlled by a frictional afterslip during a small magnitude seismic sequence (ML < 5) on the Chihshang Fault, Taiwan. _J.

Geophys. Res.: Solid xpansionwrd="Earth" ruleid="LTWA">Earth_ 123, 2003–2018 (2018). Article  ADS  Google Scholar  * Perfettini, H., Frank, W. B., Marsan, D. &

Bouchon, M. A model of aftershock migration driven by afterslip. _Geophys. Res. Lett._ 45, 2283–2293 (2018). Article  ADS  Google Scholar  * Perfettini, H., Frank, W. B., Marsan, D. &

Bouchon, M. Updip and along-strike aftershock migration model driven by afterslip: application to the 2011 Tohoku-Oki aftershock sequence. _J. Geophys. Res.: Solid Earth_ 124, 2653–2669

(2019). Article  ADS  Google Scholar  * Lippiello, E., Petrillo, G., Landes, F. & Rosso, A. Fault heterogeneity and the connection between aftershocks and afterslip. _Bull. Seismol. Soc.

Am._ 109, 1156–1163 (2019). Article  Google Scholar  * Ohnaka, M. Earthquake source nucleation: a physical model for short-term precursors. _Tectonophysics_ 211, 149–178 (1992). Article 

ADS  Google Scholar  * Dodge, D. A., Beroza, G. C. & Ellsworth, W. L. Foreshock sequence of the 1992 Landers, California, earthquake and its implications for earthquake nucleation. _J.

Geophys. Res.: Solid Earth_ 100, 9865–9880 (1995). Article  Google Scholar  * Mignan, A. Seismicity precursors to large earthquakes unified in a stress accumulation framework. _Geophys. Res.

Lett._ 39, L21308 (2012). Article  ADS  Google Scholar  * Papazachos, B. C. The time distribution of reservoir-associated foreshocks and its importance to the prediction of the principal

shock. _Bull. Seismol. Soc. Am._ 63, 1973–1978 (1973). Google Scholar  * Jones, L. M. & Molnar, P. Some characteristics of foreshocks and their possible relationship to earthquake

prediction and premonitory slip on faults. _J. Geophys. Res.: Solid Earth_ 84, 3596–3608 (1979). Article  Google Scholar  * Helmstetter, A. & Sornette, D. Foreshocks explained by

cascades of triggered seismicity. _J. Geophys. Res.: Solid Earth_ 108, 2457 (2003). ADS  Google Scholar  * Helmstetter, A., Sornette, D. & Grasso, J.-R. Mainshocks are aftershocks of

conditional foreshocks: how do foreshock statistical properties emerge from aftershock laws. _J. Geophys. Res.: Solid Earth_ 108, 2046 (2003). ADS  Google Scholar  * Felzer, K. R.,

Abercrombie, R. E. & Ekström, G. A common origin for aftershocks, foreshocks, and multiplets. _Bull. Seismol. Soc. Am._ 94, 88–98 (2004). Article  Google Scholar  * Hardebeck, J. L.,

Felzer, K. R. & Michael, A. J. Improved tests reveal that the accelerating moment release hypothesis is statistically insignificant. _J. Geophys. Res.: Solid Earth_ 113, B08310 (2008).

Article  ADS  Google Scholar  * Bouchon, M. et al. Extended nucleation of the 1999 Mw 7.6 Izmit earthquake. _Science_ 331, 877–880 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Kato,

A. et al. Propagation of slow slip leading up to the 2011 Mw 9.0 Tohoku-Oki earthquake. _Science_ 335, 705–708 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Brodsky, E. E. & Lay,

T. Recognizing foreshocks from the 1 april 2014 Chile earthquake. _Science_ 344, 700–702 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Lippiello, E., Marzocchi, W., de Arcangelis, L.

& Godano, C. Spatial organization of foreshocks as a tool to forecast large earthquakes. _Sci. Rep._ 2, 1–6 (2012). Article  CAS  Google Scholar  * Lippiello, E., Giacco, F., Marzocchi,

W., Godano, C. & Arcangelis, L. Statistical features of foreshocks in instrumental and ETAS catalogs. _Pure Appl. Geophys._ 174, 1679–1697 (2017). * Lippiello, E. Spatiotemporal

clustering of seismic occurrence and its implementation in forecasting models. in _Complexity of Seismic Time Series_ (eds Chelidze, T., Vallianatos, F. & Telesca, L.) 61–93 (Elsevier,

2018). * Lippiello, E., Godano, C. & de Arcangelis, L. The relevance of foreshocks in earthquake triggering: a statistical study. _Entropy_ 21, 173 (2019). * Nanjo, K. Z., Hirata, N.,

Obara, K. & Kasahara, K. Decade-scale decrease in b value prior to the M9-class 2011 Tohoku and 2004 Sumatra quakes. _Geophys. Res. Lett._ 39, https://doi.org/10.1029/2012GL052997

(2012). * Tormann, T., Enescu, B., Woessner, J. & Wiemer, S. Randomness of megathrust earthquakes implied by rapid stress recovery after the Japan earthquake. _Nat. Geosci._ 8, 152–158

(2015). Article  ADS  CAS  Google Scholar  * Nanjo, K. Z. & Yoshida, A. A b map implying the first eastern rupture of the Nankai trough earthquakes. _Nat. Commun._ 9, 1117 (2018).

Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Gulia, L. & Wiemer, S. Real-time discrimination of earthquake foreshocks and aftershocks. _Nature_ 574, 193–199 (2019).

Article  ADS  CAS  PubMed  Google Scholar  * Brodsky, E. Predicting if the worst earthquake has passed. _Nature_ 574, 185–186 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Burrige, R.

& Knopoff, L. Model and theoretical seismicity. _Bull. Seismol. Soc. Am._ 57, 341–371 (1967). * Deng, J., Gurnis, M., Kanamori, H. & Hauksson, E. Viscoelastic flow in the lower

crust after the 1992 Landers, California, earthquake. _Science_ 282, 1689–1692 (1998). Article  ADS  CAS  PubMed  Google Scholar  * Jagla, A., E., Landes, F. & Rosso, A. Viscoelastic

effects in avalanche dynamics: a key to earthquake statistics. _Phys. Rev. Lett._ 112, 174301 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Landes, F. P. Viscoelastic Interfaces

Driven in Dosordered Media. Ph.D. thesis LPTMS, CNRS, Université Paris Sud, Université Paris-Saclay, Orsay 91405, France. (2016). * Dieterich, J. H. Time-dependent friction as a possible

mechanism for aftershocks. _J. Geophys. Res._ 77, 3771–3781 (1972). Article  ADS  Google Scholar  * Ruina, A. Slip instability and state variable friction laws. _J. Geophys. Res.: Solid

Earth_ 88, 10359–10370 (1983). Article  Google Scholar  * Chris, M. Laboratory-derived friction laws and their application to seismic faulting. _Annu. Rev. Earth Planet. Sci._ 26, 643–696

(1998). Article  Google Scholar  * Gutenberg, B. & Richter, C. Frequency of earthquakes in California,. _Bull. Seismol. Soc. Am._ 34, 185–188 (1944). Google Scholar  * Scholz, C. H.

Scaling laws for large earthquakes: consequences for physical models. _Bull. Seismol. Soc. Am._ 72, 1–14 (1982). Google Scholar  * Working Group on California Earthquake Probabilities United

States Geological Survey. Earthquake probabilities in the San Fancisco Bay Region: 2002-2031: open-file report 03-214. na, (2003). * Bak, P. & Tang, C. Earthquakes as a self-organized

critical phenomenon. _J. Geophys. Res.: Solid Earth_ 94, 15635–15637 (1989). Article  Google Scholar  * Bak, P., Tang, C. & Wiesenfeld, K. Self-organized criticality: an explanation of

the 1/_f_ noise. _Phys. Rev. Lett._ 59, 381–384 (1987). Article  ADS  CAS  PubMed  Google Scholar  * Olami, Z., Feder, H. J. S. & Christensen, K. Self-organized criticality in a

continuous, nonconservative cellular automaton modeling earthquakes. _Phys. Rev. Lett._ 68, 1244–1247 (1992). Article  ADS  CAS  PubMed  Google Scholar  * Kawamura, H., Hatano, T., Kato, N.,

Biswas, S. & Chakrabarti, B. K. Statistical physics of fracture, friction, and earthquakes. _Rev. Mod. Phys._ 84, 839–884 (2012). Article  ADS  Google Scholar  * Freed, A. M. Earthquake

triggering by static, dynamic, and postseismic stress transfer. _Annu. Rev. Earth Planet. Sci._ 33, 335–367 (2005). Article  ADS  CAS  Google Scholar  * Nakanishi, H. Earthquake dynamics

driven by a viscous fluid. _Phys. Rev. A_ 46, 4689–4692 (1992). Article  ADS  CAS  PubMed  Google Scholar  * Hainzl, S., Zöller, G. & Kurths, J. Similar power laws for foreshock and

aftershock sequences in a spring-block model for earthquakes. _J. Geophys. Res.: Solid Earth_ 104, 7243–7253 (1999). Article  Google Scholar  * Pelletier, J. Spring-block models of

seismicity: Review and analysis of a structurally heterogeneous model coupled to a viscous asthenosphere. in _GeoComplexity and the Physics of Earthquakes Geophysical Monograph_ (eds Rundle,

J. B., Turcotte, D. L. & Klein, W.) 120–128 (American Geophysical Union, Washington, DC, 2000). * Mori, T. & Kawamura, H. Spatiotemporal correlations of earthquakes in the continuum

limit of the one-dimensional Burridge-Knopoff model. _J. Geophys. Res.: Solid Earth_ 113, B11305 (2008). Article  ADS  Google Scholar  * Kazemian, J., Tiampo, K. F., Klein, W. &

Dominguez, R. Foreshock and aftershocks in simple earthquake models. _Phys. Rev. Lett._ 114, 088501 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Aragón, L. E., Jagla, E. A. &

Rosso, A. Seismic cycles, size of the largest events, and the avalanche size distribution in a model of seismicity. _Phys. Rev. E_ 85, 046112 (2012). Article  ADS  CAS  Google Scholar  *

Jagla, E. A. Realistic spatial and temporal earthquake distributions in a modified Olami-Feder-Christensen model. _Phys. Rev. E_ 81, 046117 (2010). Article  ADS  CAS  Google Scholar  *

Jagla, E. A. & Kolton, A. B. A mechanism for spatial and temporal earthquake clustering. _J. Geophys. Res.: Solid Earth_ 115, B05312 (2010). Article  ADS  Google Scholar  * Jagla, E. A.

Delayed dynamic triggering of earthquakes: evidence from a statistical model of seismicity. _EPL (Europhys. Lett.)_ 93, 19001 (2011). Article  ADS  CAS  Google Scholar  * Jagla, E. A.

Forest-fire analogy to explain the _b_ value of the Gutenberg-Richter law for earthquakes. _Phys. Rev. Lett._ 111, 238501 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Jagla, E. A.

Aftershock production rate of driven viscoelastic interfaces. _Phys. Rev. E_ 90, 042129 (2014). Article  ADS  CAS  Google Scholar  * Landes, FmcP., Rosso, A. & Jagla, E. A. Frictional

dynamics of viscoelastic solids driven on a rough surface. _Phys. Rev. E_ 92, 012407 (2015). Article  ADS  CAS  Google Scholar  * Lippiello, E., Giacco, F., Marzocchi, W., Godano, C. &

de Arcangelis, L. Mechanical origin of aftershocks. _Sci. Rep._ 5, 1–6 (2015). Article  CAS  Google Scholar  * Landes, F. P. & Lippiello, E. Scaling laws in earthquake occurrence:

Disorder, viscosity, and finite size effects in olami-feder-christensen models. _Phys. Rev. E_ 93, 051001 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Zhang, X. & Shcherbakov, R.

Power-law rheology controls aftershock triggering and decay. _Sci. Rep._ 6, 36668 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Trugman, D. T. & Ross, Z. E.

Pervasive foreshock activity across Southern California. _Geophys. Res. Lett._ 46, 8772–8781 (2019). Article  ADS  Google Scholar  * Wetzler, N., Lay, T., Brodsky, E. E. & Kanamori, H.

Systematic deficiency of aftershocks in areas of high coseismic slip for large subduction zone earthquakes. _Sci. Adv._ 4, eaao3225 (2018). * Utsu, T. Aftershocks and earthquake statistics

(ii)—further investigation of aftershocks and other earthquake sequences based on a new classification of earthquake sequences,. _J. Fac. Sci. Hokkaido Univ., Ser. VII_ 3, 197–266 (1970).

Google Scholar  * Helmstetter, A. Is earthquake triggering driven by small earthquakes? _Phys. Rev. Lett._ 91, 058501 (2003). Article  ADS  PubMed  CAS  Google Scholar  * Amitrano, D.

Brittle-ductile transition and associated seismicity: experimental and numerical studies and relationship with the b value. _J. Geophys. Res.: Solid Earth_ 108,

https://doi.org/10.1029/2001JB000680 (2003). * W. Goebel, T. H., Schorlemmer, D., Becker, T. W., Dresen, G. & Sammis, C. G. Acoustic emissions document stress changes over many seismic

cycles in stick-slip experiments. _Geophys. Res. Lett._ 40, 2049–2054 (2013). Article  ADS  Google Scholar  * Schorlemmer D., W. M., WiemerS. Variations in earthquake-size distribution

across different stress regimes. _Nature_ 437, 539–542 (2005). Article  ADS  PubMed  CAS  Google Scholar  * Papazachos, B. Foreshocks and earthquake prediction. _Tectonophysics_ 28, 213–226

(1975). Article  ADS  Google Scholar  * Kagan, Y. Y. & Knopoff, L. Statistical study of the occurrence of shallow earthquakes. _Geophys. J. R. Astron. Soc._ 55, 67–86 (1978). Article 

ADS  Google Scholar  * Baiesi, M. & Paczuski, M. Scale-free networks of earthquakes and aftershocks. _Phys. Rev. E_ 69, 066106 (2004). Article  ADS  CAS  Google Scholar  * Baiesi, M.

& Paczuski, M. Complex networks of earthquakes and aftershocks. _Nonlinear Process. Geophys._ 12, 1–11 (2005). Article  ADS  Google Scholar  * Lippiello, E., de Arcangelis, L. &

Godano, C. Role of static stress diffusion in the spatiotemporal organization of aftershocks. _Phys. Rev. Lett._ 103, 038501 (2009). Article  ADS  CAS  PubMed  Google Scholar  Download

references ACKNOWLEDGEMENTS We thanks Eduardo Jagla for useful discussions. This research activity has been supported by the Program VAnviteLli pEr la RicErca: VALERE 2019, financed by the

University of Campania "L. Vanvitelli”. E.L. and G.P. also acknowledge support from MIUR-PRIN project "Coarse-grained description for non-equilibrium systems and transport

phenomena (CO-NEST)" no. 201798CZL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Mathematics and Physics, University of Campania “L. Vanvitelli”, Viale Lincoln 5,

Caserta, 81100, Italy Giuseppe Petrillo & Eugenio Lippiello * TAU, LRI, Univ. Paris-Sud, CNRS, INRIA, Université Paris-Saclay, Orsay, 91405, France François P. Landes * LPTMS, CNRS,

Univ. Paris-Sud, Université Paris-Saclay, Orsay, 91405, France Alberto Rosso Authors * Giuseppe Petrillo View author publications You can also search for this author inPubMed Google Scholar

* Eugenio Lippiello View author publications You can also search for this author inPubMed Google Scholar * François P. Landes View author publications You can also search for this author

inPubMed Google Scholar * Alberto Rosso View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS G.P., E.L., F.L., and A.R. have all contributed

extensively to numerical simulations, data analysis, and to write the paper. CORRESPONDING AUTHOR Correspondence to Eugenio Lippiello. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interest. ADDITIONAL INFORMATION PEER REVIEW INFORMATION _Nature Communications_ thanks Marco Baiesi, and the other, anonymous, reviewer(s) for their contribution to the

peer review of this work. Peer reviewer reports are available. PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Petrillo, G., Lippiello, E., Landes, F.P. _et al._ The influence of the

brittle-ductile transition zone on aftershock and foreshock occurrence. _Nat Commun_ 11, 3010 (2020). https://doi.org/10.1038/s41467-020-16811-7 Download citation * Received: 11 January 2020

* Accepted: 11 May 2020 * Published: 15 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16811-7 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative