Reader TTS

ABSTRACT The microscopic pair structure of superfluids has profound consequences on their properties. Delocalized pairs are predicted to be less affected by static disorder than localized

pairs. Ultracold gases allow tuning the pair size via interactions, where for resonant interaction superfluids show largest critical velocity, i.e., stability against perturbations. The

sensitivity of such fluids to strong, time-dependent disorder is less explored. Here, we investigate ultracold, interacting Fermi gases across various interaction regimes after rapid

switching optical disorder potentials. We record the ability for quantum hydrodynamic expansion of the gas to quantify its long-range phase coherence. Contrary to static expectations, the

Bose-Einstein condensate (BEC) exhibits significant resilience against disorder quenches, while the resonantly interacting Fermi gas permanently loses quantum hydrodynamics. Our findings

suggest an additional absorption channel perturbing the resonantly interacting gas as pairs can be directly affected by the disorder quench. SIMILAR CONTENT BEING VIEWED BY OTHERS LINEAR

RESPONSE OF A SUPERFLUID FERMI GAS INSIDE ITS PAIR-BREAKING CONTINUUM Article Open access 14 August 2020 UNIVERSAL KIBBLE–ZUREK SCALING IN AN ATOMIC FERMI SUPERFLUID Article 29 July 2024

SUPPRESSION OF BOGOLIUBOV MOMENTUM PAIRING AND EMERGENCE OF NON-GAUSSIAN CORRELATIONS IN ULTRACOLD INTERACTING BOSE GASES Article 03 January 2025 INTRODUCTION When an interacting system of

fermionic particles is cooled below a critical temperature, bosonic pairs form, and the system becomes superfluid or, for charged fermions, superconducting. For ultracold Fermi gases,

magnetic Feshbach resonances allow the modification of the effective interaction strength1 and thereby, the underlying pairs from small, bound molecules to delocalized Cooper-type fermion

pairs along the so-called crossover from a molecular Bose-Einstein condensate (BEC) to a Bardeen-Cooper-Schrieffer (BCS) superfluid2,3. Between these two regimes, on resonance, a unitary

Fermi gas (UFG) is realized, exhibiting, for example, the largest superfluid critical velocity along the crossover4,5. On resonance, the microscopic details of the gas are not relevant for

the macroscopic properties6, which has allowed us to deduce universal properties highly relevant for nuclear matter, for example2,3,7,8,9,10. The microscopic pairing has been investigated

theoretically11,12 and experimentally using radio-frequency (rf ) spectroscopy, for example, revealing different equilibrium properties such as the pair size or binding energy13. This

microscopic pairing has profound consequences on the macroscopic quantum state. The excitation spectrum, for example, has been measured along the crossover in three-dimensional gases using

Bragg spectroscopy14,15 and rf spectroscopy16 and shows a clear change from a phononic-type branch in the BEC regime to a spectrum indicating dominant pair breaking in the BCS regime. A

prominent consequence of the paired nature in disordered potentials is summarized by the Anderson theorem17, stating that delocalized Cooper pairs are only little affected by local

perturbations, leading to only a moderate decrease of pairs for disordered systems due to a disorder-induced reduction of the density of states close to the Fermi edge. Indeed, theoretical

investigations of the BEC-BCS crossover in static disorder18,19,20,21,22 show only a slight modification of the critical temperature in the BCS regime18, together with a relatively small

reduction of the order parameter and condensate fraction19,20, and an area of stability in the crossover region close to resonant interactions. Importantly, most studies have considered the

weak disorder regime, and theoretical investigations of strong-disorder systems beyond perturbation theory are just emerging23. Experimentally, for strong interactions, the emergence of a

fragmented Fermi gas has been observed in static disorder24. In our experiment, we consider the effect of strong and time-dependent disorder. By contrast, in the BEC regime, the critical

temperature is more strongly suppressed by static disorder, together with order parameters and condensate fraction. Experimental transport measurements indicated a disorder-induced

transition from a superfluid to a normal fluid in strong disorder25. The different behavior in the two regimes can be well explained by the fact that strong local interactions increase the

ability of the superfluid to react to local perturbations, drawing the picture of the UFG being the most resilient superfluid. However, the specific properties of the pairs are expected to

also modify the response of the superfluid to _time-dependent_ disorder and determine how fast quantum properties decay for strong perturbation, or how fast they are recovered once the

perturbation is absent. Experimental studies along the BEC-BCS crossover in the regime of static disorder regime are scarce, however, it has been shown, for example, the damping coefficient

of dipole oscillations in a static disorder potential depends on the interaction strength26. In this work, we probe the response of ultracold, interacting Fermi gases of lithium atoms in the

BEC-BCS crossover to strong perturbations in space and time via rapidly switched optical disorder potentials with a focus on the BEC side. We measure the time evolution of long-range

coherence quantified via the ability of the gas to expand hydrodynamically. We find that, in marked contrast to the expectation of the static disorder or weak-perturbation case, the quantum

properties of a UFG are more strongly suppressed than a molecular BEC (mBEC), indicating an increased sensitivity. For quenches out of a disordered potential, we find that the UFG never

restores quantum hydrodynamics for all parameters investigated, while an mBEC re-establishes quantum hydrodynamics, even when the quench leads to strong particle losses of up to 70%.

Temperature measurements indicate an additional heating channel specific for gases close to resonant interactions, leading to strong local dephasing or pair breaking. RESULTS EXPERIMENTAL

REALIZATION We experimentally study the response of an ultracold gas of fermionic lithium-6 (Li) atoms prepared in the two lowest Zeeman sub-states (typically _N__i_ = 3 ⋅ 105 atoms per spin

state _i_ = _↑_, _↓_) to fast switching of a disorder potential. The gas is prepared at a magnetic field of 763.6 G and has a temperature _T_ ≈ 200 nK, corresponding to _T_/_T_F = 0.3 in

the BEC regime at 680 G. Typical values for trap frequencies are _ω__x_, _ω__y_, _ω__z_ = 2_π_ × (345, 23, 220) Hz (see Methods). To tune the interaction between the two internal states, and

hence the pair size of the superfluids formed, a broad Feshbach resonance at a magnetic field of 832.2 G is used27. In order to prepare a different interaction regime, we adiabatically ramp

the magnetic field to the desired final value. Due to the ramp, the reduced temperature drops to values well below _T_/_T_F < 0.17 at unitarity28, implying _T_ < _T_c with the

critical temperature _T_c29. This allows entering the different regimes of the BEC-BCS crossover, quantified via the interaction parameter 1/_k_F_a_, with the absolute value of the Fermi

wave vector $${k}_{{{\rm{F}}}} =\sqrt{2m{E}_{{{\rm{F}}}}}/\hslash$$ (1) with the mass _m_ of a Li atom and the Fermi energy3 $${E}_{{{\rm{F}}}}=\hslash \bar{\omega }{(3{N}_{\uparrow

\downarrow })}^{1/3},$$ (2) the _s_-wave scattering length _a_, the geometric mean \(\bar{\omega }\) of the trap frequencies, and the total atom number _N__↑__↓_ in both spin states. The

typical value for the Fermi energy is _E_F ≈ _k__B_ × 670 nK, with _k__B_ the Boltzmann constant. Table 1 shows typical experimental parameters for the quantum gas at different magnetic

fields. Our observable revealing the response of quantum properties is the ability of the gas to undergo quantum hydrodynamic expansion. Expansion measurements probing hydrodynamic behavior

have been used, for example, to characterize the transition between ballistic and hydrodynamic expansion30 and to study the viscosity in a UFG31. Here, we employ hydrodynamic expansion as a

measure of long-range phase coherence32. It allows us to time-resolve a quantum system’s response to a strong perturbation in space and time, revealing the existence or reformation of a

well-defined global phase. We can thus trace a genuine quantum property of a strongly interacting, three-dimensional many-body system subjected to strong and time-dependent perturbation. In

a previous work32, performed with the same experimental apparatus, we focused on investigations deep in the mBEC regime. Here, we extend this study by focussing on the markedly different

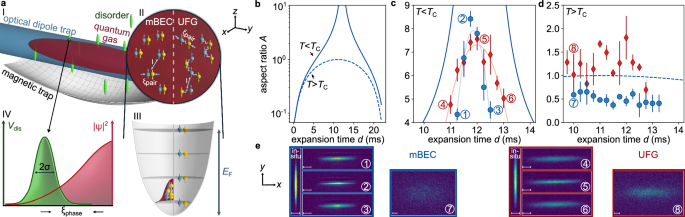
stability and sensitivity of an mBEC compared to a UFG. Hydrodynamics is initiated by suddenly switching off the optical dipole trap (see Fig. 1a), releasing the gas into a magnetic trap

with a saddle potential configuration (confining in the _x_-_y_ plane and anti-confining in the _z-_direction), where the change of aspect ratio _A_ can be determined from absorption images.

Here, the aspect ratio is defined as the ratio of the full width at half maximum (FWHM) of the 1D integrated column density distributions in _x_ and _y_ directions (see Fig. 1a and

Supplementary Note 1A). The ensuing dynamics are markedly different for an ideal gas, a classical (thermal) interacting gas or a quantum gas33. While an ideal gas shows a moderate change in

aspect ratio due to single-particle dynamics in the trap, this change is enhanced by collisional hydrodynamics for repulsively interacting classical gases (see Fig. 1b, d, e). Quantum gases,

however, show a remarkably large change in aspect ratio, as shown in Fig. 1b, c, e. This strong increase beyond classical collisional hydrodynamics is tightly connected to the existence of

a well-defined global phase, i.e., long-range phase coherence32. We note that a comparable quantum enhancement cannot be observed for the BCS side of the resonance, i.e., negative

interaction parameters 1/_k_F_a_ < 0 even close to resonance, in agreement with previous observations of the vanishing of hydrodynamics when approaching the BCS regime34. We attribute

this to the breaking of the underlying fermionic pairs due to the strongly reduced density and, hence, paring gap during the expansion. Our analysis is therefore restricted to positive

interaction parameters 1/_k_F_a_ ≥ 0 which will be the focus throughout the remainder of this work. For more details of the experimental setup, see Methods and ref. 35. The perturbation of

the system is controlled through a repulsive optical speckle disorder-potential with mean potential strength \({\bar{V}}_{{{\rm{dis}}}}\) and correlation lengths of _σ__x_,_y_ = 750 nm, and

_σ__z_ = 10 μm, see Fig. 1a. Here, the correlation length is defined as the 1/_e_ − width of the speckle pattern’s autocorrelation function and quantifies the typical grain size32. The mean

potential strength is of the order of the superfluid’s chemical potential _μ_ (_μ_BEC = _k__B_ × 390 nK for a mBEC and _μ_UFG = _k__B_ × 480 nK for a UFG) and the short correlation length is

larger but of the order of the quantum gases’ coherence or healing length _ξ_ (_ξ_heal ≈ 230 nm for 1/_k_F_a_ ≈ 1). Thus, the static perturbation is strong. Since the polarizability of a

Feshbach molecule is twice as high as that of a single atom, the potential height of the speckle potential for the molecules is twice as high as for the unbound atoms at the same laser

power36,37. In tunneling experiments along the BEC-BCS crossover, for example, this does not seem to play a role, and the dynamics for constant optical potentials along the crossover could

be compared38,39. Measurements for atom losses after disorder quenches (see Supplementary Note 1B) show, however, that the loss curves collapse to a single curve, when the disorder laser

power for the UFG is twice the power for a mBEC, supporting our assumption of different potentials _V_ (mBEC) ≈ 2 _V_(UFG) for the same laser power. This observation indicates that the

disorder locally affects molecules in the mBEC and atoms in the UFG. In the following, the disorder is given in laser power of the disorder, providing a comparison of potential heights

differing by a factor of two. Moreover, the disorder potential can be either ramped adiabatically with respect to _h_/_μ_ or be quickly switched on or off with switching times being shorter

than _h_/_μ_ (see insets of Figs. 2a, 3a), so that the many-body system cannot adiabatically follow the dynamics. The speckle realization is changed after each measurement. Furthermore, for

our parameters, classical trapping cannot occur, because the mobility edge is close to the classical percolation threshold in our system36,40. For a detailed description and characterization

of the disorder potential see Methods and Refs. 23,41,42. DECAY OF QUANTUM HYDRODYNAMICS We first study the impact of a suddenly applied disorder potential on a superfluid in different

interaction regimes. We thus analyze the collapse of the hydrodynamic expansion after a sudden quench into the disorder potential of variable duration _τ_on. In addition to studying the

hydrodynamic behavior, we have additionally examined the density response for all measurements along the crossover shown in the following and report it in Supplementary Note 2. In Fig. 2a,

we compare the decay of the maximum achievable aspect ratio of hydrodynamic expansion of a mBEC (1/_k_F_a_ = 1.04) and a UFG at resonance (1/_k_F_a_ = 0) below the critical temperature as a

function of _τ_on. All data are normalized to the maximum aspect ratio change experimentally obtained without the disorder, see Fig. 1c. Here, for the mBEC regime, the speckle laser power is

set to 5 W, corresponding to \({\bar{V}}_{{{\rm{dis}}}}^{{{\rm{mBEC}}}}/{\mu }_{{{\rm{mBEC}}}}\approx 1.6\) and 10 W for the UFG \({\bar{V}}_{{{\rm{dis}}}}^{{{\rm{UFG}}}}/{\mu

}_{{{\rm{UFG}}}}\approx 1.3\), ensuring approximately the same, strong disorder potential height in the two regimes. As seen in Fig. 2a, the maximum aspect ratio decreases after suddenly

applying the disorder potential for a certain time _τ_on approximately exponentially, indicating a collapse of quantum hydrodynamics and hence, long-range coherence. The minimum aspect ratio

reached in a steady state corresponds to the respective aspect ratio of a thermal gas in the mBEC regime or at resonance. We find that the UFG stabilizes at a higher value of the aspect

ratio compared to the mBEC, which we attribute to higher interaction strength and hence, stronger classical hydrodynamics in this regime. As shown in the Methods, the change in aspect ratio

depends on the trap frequencies rather than potential depth. Therefore, the difference in classical hydrodynamics cannot be due to the different masses of molecules compared to atoms. The

half-life period _τ_1/2, i.e., the time at which the aspect ratio has collapsed to half of the initial value, of the UFG is shorter with (7 ± 1) μs than for the mBEC with (11 ± 2) μs . From

studies in the mBEC regime32, a relatively constant _τ_1/2 value was found for a broad range of interaction parameters outside the crossover 1/_k_F_a_ > 1. The underlying mechanism

explaining the time scales and numerical simulations of the phase evolution suggested the imprinting of a random local phase onto the mBEC by the disorder. The resulting local phase

evolution destroys long-range phase coherence, and for a broad range of interaction strengths, it is only dependent on the properties of the disorder potential but not on interaction

properties. In Fig. 2b, we show the _τ_1/2 values when entering the crossover. The clearly faster decay of long-range phase coherence indicates that the decay now does depend on interaction,

in contrast to deep in the weakly interacting BEC regime (1/_k_F_a_ ≫ 1). Hence, an additional mechanism suppressing long-range phase coherence is present in the crossover. To illustrate

this, we compare the half-life period with a heuristic dephasing time _t_ph = _ℏ_/_Δ__E_, which describes the time it takes for the two-particle wave function of the pair to accumulate a

phase shift of unity due to a potential difference _Δ__E_ in the disorder field. A Feshbach molecule experiences a reduced potential difference compared to a more delocalized Cooper pair due

to its smaller spatial extension. The decay of the half-life period by entering the crossover shows a qualitatively similar behavior as the decrease of the dephasing time, illustrating that

a microscopic mechanism perturbing the pair structure could become relevant in the crossover. REVIVAL OF QUANTUM HYDRODYNAMICS Complementary, we study the revival of the long-range phase

coherence when the system is quenched out of a disordered potential. Experimentally, we adiabatically ramp up the speckle potential in a 50 ms linear ramp to avoid excitations in the cloud.

The potential is held for 100 ms before suddenly switching off the disorder, see inset in Fig. 3a. After a varying hold time _τ_off without the disorder, the cloud is expanded for a time _d_

into the magnetic saddle potential to allow for hydrodynamic expansion before imaging. The two regimes of mBEC and UFG show strikingly different behavior, illustrated in Fig. 3a, b. While

the long-range phase coherence for the mBEC recovers completely with an exponential time constant \({\tau }_{1/2}^{{{\rm{off}}}}=\,(20\,\pm \,3){{\rm{ms}}}\), the UFG does not fully revive.

We show the maximum achievable value of the aspect ratio in Fig. 3c along the crossover without disorder and for two different disorder laser powers. Without disorder, we find a maximum

aspect ratio that slightly increases for decreasing interaction parameter 1/_k_F_a_ in the crossover, until it rapidly decays for negative scattering length, i.e., on the BCS side of the

crossover 1/_k_F_a_ < 0. For the strongest disorder applied, the gas quenched out of the disorder behaves similarly to a classical gas for all interaction strengths. An interesting

behavior is observed for intermediate disorder laser powers. Here, the gas can fully revive in the mBEC regime, which is consistent with previous studies32. For decreasing interaction

parameter 1 > 1/(_k_F_a_) > 0.5, the maximum aspect ratio decays and approaches the classical limit until it increases again for 0.5 > 1/(_k_F_a_) > 0. However, for all

interaction strengths in the crossover, quantum hydrodynamics does not revive, in stark contrast to the mBEC regime outside the crossover. This is even more remarkable since, for the

equilibrium, weak-disorder phase diagram, the critical temperature in the mBEC regime is expected to be more strongly reduced with the disorder compared to the UFG18,43. In order to

characterize the many-body state after the quench, we additionally measure the temperature increase for different disorder ramp procedures, (see Methods). In Fig. 3d–f, we show the relative

temperature increase for the limiting cases of an mBEC and a UFG for a fully adiabatic ramp, a disorder pulse (as used in Fig. 2), and rapid quench out of disorder (as used in Fig. 3a, c).

For the fully adiabatic ramp (Fig. 3d), neither mBEC nor UFG shows a significant increase in temperature. For a quench pulse, i.e., a quench into and a quench out-of the disorder (Fig. 3e),

both gases are significantly heated and show a similar increase in temperature. While the relatively large error bars do not allow the identification of the speckle power when the gas is

heated above the critical temperature, for the highest disorder potential, the UFG shows _T_ > _T_c. Interestingly, for an adiabatic loading into the disorder potential and a subsequent

quench out of disorder, Fig. 3f, the UFG is heated more strongly than the mBEC, whereas for a speckle laser power of 10 W, the UFG is brought above the critical temperature, while the mBEC

is mainly unaffected. The maximum thermal energy increase in Fig. 3f for the UFG is _Δ__E_/_E_F ≈ 0.09, which may be compared to the energy needed for pair breaking 2_Δ_gap = 1.8_E_F44. The

energy absorbed by the UFG from the quench thus brings the gas close to or above the critical temperature, and quantum hydrodynamic expansion breaks down. In order to check if the

temperature increase is the main reason for the collapse of quantum hydrodynamics, we study disorder quenches in an open system, where high-energetic particles can escape from the trap,

effectively reducing the mean energy. This is achieved by reducing the depth of the optical dipole trap, allowing a certain fraction of atoms with the highest energy to escape. The relation

between the fraction of particles lost and the potential depth is shown in Supplementary Note 3. We find that, even for losses of more than 60 %, the mBEC recondenses and shows a

close-to-full revival of hydrodynamic expansion, and hence long-range coherence. By contrast, the UFG does not show a significant increase in quantum hydrodynamics for any particle loss.

DISCUSSION Our data suggests that even for a UFG initially adiabatically prepared to populate the ground state of a disorder potential, a quench out of disorder permanently destroys

long-range quantum coherence. This is in stark contrast to the equilibrium expectation, where a UFG has so far been found to form a superfluid showing the largest critical velocity. The

temperature measurements suggest the appearance of an additional absorption channel for the UFG, which is not present for the mBEC. This additional heating brings the UFG close to or above

the critical point, and quantum hydrodynamic ceases. A first intuitive understanding of the microscopic origin of this heating channel can be obtained by considering the microscopic pairing

structure along the BEC-BCS crossover11,45,46,47. Figure 4a compares relevant energies of the quenched disorder potential with energy scales of the many-body system, especially the many-body

gap 2_Δ_gap and the molecular binding energy _E_B = _ℏ_2/(_m__a_2)34, in the BEC-BCS crossover. Calculations are done using experimental parameters, specifically total atom number _N__↑__↓_

 = 5.13 × 105 (average of experimental values) and trap frequencies _ω__x_, _ω__y_, _ω__z_ = 2_π_ × (345, 23, 220) Hz. The Fermi energy is calculated according to eq. (2). Besides, the mean

disorder potential strength \({\bar{V}}_{{{\rm{dis}}}}\) is shown, and the correlation energy _E__σ_ = _ℏ_2/(_m__σ_2)48 is calculated. These two quantities are different for atoms or

molecules at the same laser power due to the difference in mass. The energy scale of the quench time of the speckle field is given by _E_quench = _ℏ_/_t_on, where the time to switch on the

speckle field instantaneously is measured with _t_on = 2.26 μs. Figure 4b shows the change of coherence lengths _ξ_pair and _ξ_phase of the interacting many-body system along the BEC-BCS

crossover, see refs. 11,45,46,47. Deep in the mBEC regime, both differ significantly. The molecules are relatively small, and the healing length _ξ_ = _ξ_phase is much larger, increasing for

larger interaction parameters 1/(_k_F_a_). Hence, _ξ_phase > _ξ_pair. Approaching the resonance, the healing length decreases, while the molecules become larger as the molecular bound

state energy approaches the dissociation threshold. Upon entering the crossover 1/(_k_F_a_) ≈ 1, the two length scales approximately coincide _ξ_phase = _ξ_pair. On resonance, the pair

coherence length is larger than the phase coherence length. In the BCS regime, the two quantities scale the same and differ only by some constant factor. The coherence lengths allow for

estimating the effect of local potential changes on the fermionic pair. Comparing these scales with energy and length scales of the quenched disorder potential, we find that, first, deep in

the mBEC regime, the pair size is much smaller than any length scale of the disorder potential. At the same time, the molecular binding energy is so large that no energy scale of the

disorder is comparable. Thus, the disorder potential primarily affects the global wave function, which is perturbed at the length scale of the healing length and the energy scale of the

chemical potential, leading to wave-like excitations of the many-body system. In the crossover, however, the pair size increases and becomes of the order of the healing length, being smaller

but of the order of the correlation length of the disorder, where the UFG shows the largest pair size of the order of 1/_k_F. As shown in the inset of Fig. 2b, local gradients of the

disorder hence become relevant on the length scale of the pair. At the same time, the many-body gap, as well as the binding energy of the molecular state, decreases when approaching the

resonance 1/_k_F_a_ → 0. Here, the energy scales of the time-dependent disorder, specifically the inverse ramping time _E_quench = _ℏ_/_t_on, but also the correlation energy _E__σ_ = 

_ℏ_2/(_m__σ_2)48 or mean potential strength \({\bar{V}}_{{{\rm{dis}}}}\), become compatible to or larger than the many-body gap or the binding energy _E_B = _ℏ_2/(_m__a_2)34 for sufficiently

strong interaction. Hence, pair breaking can occur. This microscopic matching of pair properties to the length and energy scales of the quenched disorder can explain the additional

absorption channel for energy in the UFG. It brings the many-body system close to or even above the critical temperature, where quantum dynamics cease. For two-dimensional strongly

disordered superconductors, it was shown in ref. 49 that the strongly disordered many-body system can form superconducting islands separated by an insulating sea, where the islands are not

phase coherent. A fragmented Fermi gas, comprising unconnected islands of bound pairs in strong disorder, was proposed in ref. 24 to explain the experimentally observed density modulations.

Our system is three-dimensional, and our disorder is formed by a repulsive potential far from the percolation threshold so the system is expected to be always fully connected. However, our

observation might point toward a local dephasing of the UFG by strong disorder quenches, potentially at the level of individual pairs. It will be interesting in the future to see if the UFG

quenched out of strong disorder might contain islands of Fermi pairs that connect to a smooth density but preserve phase differences that prevent global quantum hydrodynamic expansion. Our

studies of the stability of interacting Fermi superfluids along the BEC-BCS crossover in the presence of a strong time-dependent perturbation clearly show that the static properties of the

disordered BEC-BCS crossover are very different from the observations obtained in this work for the time-dependent nonequilibrium case. In the future, it will be interesting to

quantitatively map out the phase diagram of the disordered BEC-BCS crossover away from equilibrium. In addition, reducing the dimensionality of the gas and producing homogeneous gases in

different dimensions will provide a deeper and more quantitative insight into the connection between the microscopic pairing mechanism and macroscopic nonequilibrium dynamics. METHODS

QUANTUM-GAS PREPARATION We evaporate our laser-cooled samples at a magnetic field of 763.6 G (_a_ = 4509_a_0, with the Bohr radius _a_0) in the mBEC regime for all observed interacting

regimes. During evaporation, the laser power of the optical-dipole trap (ODT) is lowered from 140 mW to 8 mW by two subsequent exponential power ramps during 4.38 s. This final laser power

of 8 mW is relatively low and enables controlling atom losses through disorder quenches. After the evaporation step, the laser power is held for 250 ms to equilibrate the temperature of the

cloud. Subsequently, the trap is compressed by increasing the optical-dipole-trap (ODT) laser power up to 80 mW during 300 ms. By varying the level of compression, the amount of losses due

to the disorder field can be adjusted. No losses occur at a power of 80 mW. After the condensate is formed, the magnetic field is adiabatically ramped to the desired field for interaction

control during 200 ms. The cloud is trapped in a combination of the ODT, created with a focused laser beam of a wavelength of 1070 nm and a magnetic saddle potential. Further, the magnetic

field strength determines the scattering length and, therefore, the interacting regime between the two spin states. Before disturbing the cloud by quenching the disorder field, another

holding time of 30 ms ensures that no excitations of the cloud are present after changing the magnetic field strength. The trap frequencies in the radial directions, _x_ and _z_, increase

with the square root of the laser power of the ODT. The axial trap frequency, _y_ direction, is within the range used, independent of the laser power. Changing the magnetic field has a

negligible influence on the trap frequency compared to the genuine frequency. The trap frequencies are _ω__x_, _ω__y_, _ω__z_ = 2_π_ × (345, 23, 220) Hz for an ODT laser power of 80 mW and a

magnetic field strength of 763.6 G. DISORDER POTENTIAL A far-off resonant, blue-detuned laser with a wavelength of 532 nm generates the potential. The envelope of the laser is a Gaussian

with waists of (466 ± 25) μm and (414 ± 25) μm along two orthogonal directions50. Moreover, the optical speckle potential is formed by shining the collimated laser beam through two

successive speckle plates. An objective focuses the random phase pattern on the position of the atoms. Hence, anisotropic speckle grains with sizes _σ__x_,_y_ = 750 nm, and _σ__z_ = 10 μm

are formed. The speckle plates are mounted in a motorized turntable; one of them is rotated by a certain angle after each measurement so that the interference potential changes in each

experimental realization. We characterize the strength of the disorder potential _V_dis by the mean disorder potential \({\bar{V}}_{{{\rm{dis}}}}\), which is the overall spatial average. For

comparison, we may express the mean disorder potential in units of the unperturbed chemical potential. For the mBEC, the chemical potential51 $${\mu }_{{{\rm{mBEC}}}}=\frac{\hslash

\bar{\omega }}{2}{\left(\frac{15\frac{{N}_{\uparrow \downarrow }}{2}{a}_{{{\rm{dd}}}}}{{a}_{{{\rm{ho}}}}}\right)}^{2/5}$$ (3) is established through the Gross-Pitaevskii equation, where

_a_dd = 0.6_a_52 is the _s_-wave scattering length for molecules, \({a}_{{{\rm{ho}}}}=\sqrt{\hslash /(2m\bar{\omega })}\) the harmonic oscillator length with the mass _m_ of the lithium

atom. The chemical potential of the UFG53 $${\mu }_{{{\rm{UFG}}}}=\sqrt{1+\beta }{E}_{{{\rm{F}}}}$$ (4) is proportional to the Fermi energy with the universal constant \(\sqrt{1+\beta }\).

DEPENDENCE OF THE EXPANSION DYNAMICS ON INTERACTIONS An mBEC and a UFG show quantum hydrodynamic expansion34. In the case of an mBEC, a UFG, or a thermal gas, the in-situ aspect ratio is

independent of the mass of the particles. The radii for all three cases individually depend on the mass, but it cancels when computing the aspect ratio. Instead, the aspect ratio depends on

the trap frequencies. During expansion, the aspect ratio \(\frac{{R}_{x}(t)}{{R}_{y}(t)}=\frac{{b}_{x}(t)}{{b}_{y}(t)}\frac{{\omega }_{y}}{{\omega }_{x}}\) changes according to scaling

factors _b__i_ $${\ddot{b}}_{i}-\frac{{\omega }_{i}^{2}}{{b}_{i}{({b}_{x}{b}_{y}{b}_{z})}^{\gamma }}=0,$$ (5) which can be derived from the Euler equation34. The scaling factors are

independent of the mass. The expansion of the mBEC and the UFG differ by the exponent gamma (BEC _γ_ = 1, UFG _γ_ = 2/3) since the difference of the chemical potential depends on the density

in the two regimes (_μ_BEC ∝ _n_, _μ_UFG ∝ _n_2/3)54. Moreover, the trap frequencies are identical for a Feshbach molecule or a single atom, and hence the aspect ratio during expansion is

independent of the mass of the particles. A thermal gas shows a ballistic expansion with scaling factors also independent of the particle mass. DETERMINATION OF THE HALF-LIFE PERIOD BY

EXPANSION DYNAMICS For the decay and the revival of the long-range phase coherence (where the cloud fully recovers), the half-life period _τ_1/2 is determined similar to ref. 32. When

plotting the aspect ratio as a function of the speckle-pulse length _τ_on or the revival time _τ_off, it shows an exponential evolution to a steady state. This behavior is fitted with an

exponential decay function (see Figs. 2a, 3a) $$h(\tau )=a\,{e}^{-\gamma \tau }+o,$$ (6) with _γ_ is the decay constant and _o_ and _a_ are further fit values. Here, the half-life period is

calculated via $${\tau }_{1/2}=\ln (2)/\gamma .$$ (7) The uncertainty of the half-life period is taken as the fit uncertainty. TEMPERATURE MEASUREMENTS We have measured the relative

temperature increase in the quantum gases for a mBEC at 763.6 G and a UFG at 832.2 G through the disorder potential for different disorder ramp procedures (see Fig. 3d–f) applying up to 10 W

laser power creating the disorder field. As a reference, we measure the gas temperature _T_0 without the disorder field. Three disorder ramping procedures are investigated. First (Fig. 3d),

the disorder field is adiabatically introduced by a linear ramp during a 50 ms, held for 100 ms, and subsequently switched off at 50 ms by a linear ramp. Second (Fig. 3e), the disorder is

rapidly switched on (switching time of _t_on = 2.26 μs) for a rectangular pulse for a duration of duration _τ_on = 100 ms. Lastly (Fig. 3f), the disorder field is adiabatically introduced by

a linear ramp during a 50 ms, and subsequently, the power is held for 100 ms, before the field is suddenly switched off. After a holding time of 100 ms, the magnetic field is adiabatically

swept to 680 G. Subsequently, the cloud is imaged in situ via absorption imaging. At this magnetic field strength, a bimodal fit to the density profiles allows the extraction of the

temperature of the cloud. DATA AVAILABILITY All data of the figures in the manuscript are available in a Zenodo repository, Ref. 55, https://doi.org/10.5281/zenodo.13292670. REFERENCES *

Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. _Rev. Mod. Phys._ 82, 1225 (2010). Article  ADS  CAS  Google Scholar  * Sá de Melo, C. A. R. When

fermions become bosons: Pairing in ultracold gases. _Phys. Today_ 61, 45 (2008). Article  Google Scholar  * Zwerger, W._The BCS-BEC Crossover and the Unitary Fermi Gas_ (Springer, 2012). *

Miller, D. E. et al. Critical velocity for superfluid flow across the BEC-BCS crossover. _Phys. Rev. Lett._ 99, 070402 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Weimer, W. et al.

Critical velocity in the BEC-BCS crossover. _Phys. Rev. Lett._ 114, 095301 (2015). Article  ADS  PubMed  Google Scholar  * Randeria, M. & Taylor, E. Crossover from

Bardeen-cooper-Schrieffer to bose-einstein condensation and the unitary Fermi gas. _Annu. Rev. Condens. Matter Phys._ 5, 209 (2014). Article  ADS  CAS  Google Scholar  * Strinati, G. C.,

Pieri, P., Röpke, G., Schuck, P. & Urban, M. The BCS-BEC crossover: From ultra-cold Fermi gases to nuclear systems. _Phys. Rep._ 738, 1 (2018). Article  ADS  MathSciNet  CAS  Google

Scholar  * Shen, G., Horowitz, C. J. & Teige, S. Equation of state of nuclear matter in a virial expansion of nucleons and nuclei. _Phys. Rev. C._ 82, 045802 (2010). Article  ADS  Google

Scholar  * Carlson, J., Gandolfi, S. & Gezerlis, A. Quantum Monte Carlo approaches to nuclear and atomic physics. _Prog. Theor. Exp. Phys._ 2012, 01A209 (2012). Article  Google Scholar

  * Gezerlis, A. & Carlson, J. Strongly paired fermions: Cold atoms and neutron matter. _Phys. Rev. C._ 77, 032801 (2008). Article  ADS  Google Scholar  * Engelbrecht, J. R., Randeria,

M. & Sá de Melo, C. A. R. BCS to Bose crossover: Broken-symmetry state. _Phys. Rev. B_ 55, 15153 (1997). Article  ADS  CAS  Google Scholar  * Sá de Melo, C. A. R., Randeria, M. &

Engelbrecht, J. R. Crossover from BCS to Bose superconductivity: Transition temperature and time-dependent Ginzburg-Landau theory. _Phys. Rev. Lett._ 71, 3202 (1993). Article  ADS  Google

Scholar  * Schunck, C. H., Shin, Y., Schirotzek, A. & Ketterle, W. Determination of the fermion pair size in a resonantly interacting superfluid. _Nature_ 454, 739 (2008). Article  ADS 

CAS  PubMed  Google Scholar  * Biss, H. et al. Excitation spectrum and superfluid gap of an ultracold Fermi gas. _Phys. Rev. Lett._ 128, 100401 (2022). Article  ADS  CAS  PubMed  Google

Scholar  * Hoinka, S. et al. Goldstone mode and pair-breaking excitations in atomic Fermi superfluids. _Nat. Phys._ 13, 943 (2017). Article  CAS  Google Scholar  * Chin, C. et al.

Observation of the pairing gap in a strongly interacting Fermi gas. _Science_ 305, 1128 (2004). Article  ADS  CAS  PubMed  Google Scholar  * Anderson, P. Theory of dirty superconductors. _J.

Phys. Chem. Solids_ 11, 26 (1959). Article  ADS  CAS  Google Scholar  * Han, L. & Sá de Melo, C. A. R. Evolution from Bardeen-Cooper-Schrieffer to Bose-Einstein condensate superfluidity

in the presence of disorder. _N. J. Phys._ 13, 055012 (2011). Article  Google Scholar  * Orso, G. BCS-BEC Crossover in a random external potential. _Phys. Rev. Lett._ 99, 250402 (2007).

Article  ADS  CAS  PubMed  Google Scholar  * Khan, A., Basu, S. & Kim, S. W. Effect of disorder in BCS-BEC crossover. _J. Phys. B At. Mol. Opt. Phys._ 45, 135302 (2012). Article  ADS 

Google Scholar  * Palestini, F. & Strinati, G. C. Systematic investigation of the effects of disorder at the lowest order throughout the BCS-BEC crossover. _Phys. Rev. B_ 88, 174504

(2013). Article  ADS  Google Scholar  * Joshi, A. & Majumdar, P. Impact of speckle disorder on a superfluid Fermi system. _Phys. Rev. B_ 100, 045149 (2019). Article  ADS  CAS  Google

Scholar  * Nagler, B. et al. Cloud shape of a molecular Bose-Einstein condensate in a disordered trap: a case study of the dirty boson problem. _N. J. Phys._ 22, 033021 (2020). Article 

MathSciNet  CAS  Google Scholar  * Krinner, S., Stadler, D., Meineke, J., Brantut, J.-P. & Esslinger, T. Observation of a fragmented, strongly interacting Fermi gas. _Phys. Rev. Lett._

115, 045302 (2015). Article  ADS  PubMed  Google Scholar  * Krinner, S., Stadler, D., Meineke, J., Brantut, J.-P. & Esslinger, T. Superfluidity with disorder in a thin film of quantum

gas. _Phys. Rev. Lett._ 110, 100601 (2013). Article  ADS  PubMed  Google Scholar  * Nagler, B. et al. Dipole oscillations of fermionic quantum gases along the BEC-BCS crossover in disordered

potentials. _Phys. Rev. A_ 101, 053633 (2020). Article  ADS  CAS  Google Scholar  * Zürn, G. et al. Precise characterization of 6Li Feshbach resonances using trap-sideband-resolved RF

spectroscopy of weakly bound molecules. _Phys. Rev. Lett._ 110, 135301 (2013). Article  ADS  PubMed  Google Scholar  * Chen, Q., Stajic, J. & Levin, K. Thermodynamics of interacting

Fermions in atomic traps. _Phys. Rev. Lett._ 95, 260405 (2005). Article  ADS  PubMed  Google Scholar  * M. Ku, L. C., Sommer, A. & Zwierlein, M. Revealing the superfluid Lambda

transition in the universal thermodynamics of a unitary Fermi gas. _Science_ 335, 563 (2012). Article  ADS  Google Scholar  * O’Hara, K. M., Hemmer, S. L., Gehm, M. E., Granade, S. R. &

Thomas, J. E. Observation of a strongly interacting degenerate Fermi gas of atoms. _Science_ 298, 2179 (2002). Article  ADS  PubMed  Google Scholar  * Cao, C. et al. Universal quantum

viscosity in a unitary Fermi gas. _Science_ 331, 58 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Nagler, B., Barbosa, S., Koch, J., Orso, G. & Widera, A. Observing the loss and

revival of long-range phase coherence through disorder quenches. _Proc. Natl. Acad. Sci. USA_ 119, e2111078118 (2022). Article  CAS  PubMed  Google Scholar  * Wright, M. J. et al.

Finite-temperature collective dynamics of a Fermi gas in the BEC-BCS crossover. _Phys. Rev. Lett._ 99, 150403 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Giorgini, S., Pitaevskii,

L. P. & Stringari, S. Theory of ultracold atomic Fermi gases. _Rev. Mod. Phys._ 80, 1215 (2008). Article  ADS  CAS  Google Scholar  * Gänger, B., Phieler, J., Nagler, B. & Widera, A.

A versatile apparatus for fermionic lithium quantum gases based on an interference-filter laser system. _Rev. Sci. Instrum._ 89, 093105 (2018). Article  ADS  PubMed  Google Scholar  *

Gänger, B., _Towards a Degenerate Fermi Gas in a Disordered Environment_, Ph.D. thesis, University of Kaiserslautern, Supervisor: Artur Widera (2019). * Jochim, S. et al. Pure gas of

optically trapped molecules created from Fermionic atoms. _Phys. Rev. Lett._ 91, 240402 (2003). Article  ADS  CAS  PubMed  Google Scholar  * Valtolina, G. et al. Josphson effect in fermionic

superfluids across the BEC-BCS crossover. _Science_ 350, 1505 (2015). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Kwon, W. et al. Strongly correlated superfluid order

parameters from dc Josephson supercurrents. _Science_ 369, 84 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Shapiro, B. Cold atoms in the presence of disorder. _J. Phys. A: Math.

Theor._ 45, 143001 (2012). Article  ADS  Google Scholar  * Nagler, B. et al. Ultracold bose gases in dynamic disorder with tunable correlation time. _Phys. Rev. Lett._ 128, 233601 (2022).

Article  ADS  CAS  PubMed  Google Scholar  * Hiebel, S., Nagler, B., Barbosa, S., Koch, J., and Widera, A. Characterizing quantum gases in correlated-disorder realizations using

density-density correlations. _New J. Phys_. 26, 013042 (2024). * Lopatin, A. V. & Vinokur, V. M. Thermodynamics of the superfluid dilute bose gas with disorder. _Phys. Rev. Lett._ 88,

235503 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Grimm, R. Ultracold Fermi gases in the BEC-BCS crossover: a review from the Innsbruck perspective. In _Proc. International School

of Physics “Enrico Fermi_” 413–462 (IOS Press Ebooks, 2007). * Marini, M., Pistolesi, F. & Strinati, G. Evolution from BCS superconductivity to Bose condensation: analytic results for

the crossover in three dimensions. _Eur. Phys. J. B_ 1, 151 (1998). Article  ADS  CAS  Google Scholar  * Pistolesi, F. & Strinati, G. C. Evolution from BCS superconductivity to Bose

condensation: Calculation of the zero-temperature phase coherence length. _Phys. Rev. B_ 53, 15168 (1996). Article  ADS  CAS  Google Scholar  * Pistolesi, F. & Strinati, G. C. Evolution

from BCS superconductivity to Bose condensation: Role of the parameter _k__F__ξ_. _Phys. Rev. B_ 49, 6356 (1994). Article  ADS  CAS  Google Scholar  * Delande, D. & Orso, G. Mobility

edge for cold atoms in laser speckle potentials. _Phys. Rev. Lett._ 113, 060601 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Ghosal, A., Randeria, M. & Trivedi, N. Inhomogeneous

pairing in highly disordered s-wave superconductors. _Phys. Rev. B_ 65, 014501 (2001). Article  ADS  Google Scholar  * Nagler, B. _Bose-Einstein Condensates and Degenerate Fermi Gases in

Static and Dynamic Disorder Potentials_, Ph.D. thesis, University of Kaiserslautern, Supervisor: Artur Widera (2020). * Pitaevskii, L. and Stringari, S., _Bose-Einstein Condensation and

Superfluidity_ (Oxford University Press, 2016). * Petrov, D. S., Salomon, C. & Shlyapnikov, G. V. Weakly bound dimers of fermionic atoms. _Phys. Rev. Lett._ 93, 090404 (2004). Article 

ADS  CAS  PubMed  Google Scholar  * Kinast, J. et al. Heat capacity of a strongly interacting Fermi gas. _Science_ 307, 1296 (2005). Article  ADS  CAS  PubMed  Google Scholar  * Ketterle, W.

& Zwierlein, M. W. Making, probing and understanding ultracold Fermi gases. _La Rivista del Nuovo Cimento_ 31, 247–422 (2008). * Koch, J., Barbosa, S., Lang, F., and Widera, A.,

Stability and sensitivity of interacting fermionic superfluids to quenched disorder [Data set], Zenodo https://doi.org/10.5281/zenodo.13292670 (2024). Download references ACKNOWLEDGEMENTS We

thank Carlos A. R. Sá de Melo, Henning Moritz, Giuliano Orso, Giacomo Roati, Wilhelm Zwerger, Benjamin Nagler, and Alexander Guthmann for helpful discussions and Eloisa Cuestas for

carefully reading the manuscript. This work was supported by the German Research Foundation (DFG) via the Collaborative Research Center Sonderforschungsbereich SFB/TR185 (Project 277625399).

J.K. was supported by the Max Planck Graduate Center with the Johannes Gutenberg-Universität Mainz. We acknowledge the help by Valeriya Mikhaylova with the graphical implementation of Fig. 

1a. FUNDING Open Access funding enabled and organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Physics and Research Center OPTIMAS, RPTU

Kaiserslautern-Landau, Kaiserslautern, Germany Jennifer Koch, Sian Barbosa, Felix Lang & Artur Widera * TOPTICA Photonics AG, Gräfelfing, Germany Jennifer Koch Authors * Jennifer Koch

View author publications You can also search for this author inPubMed Google Scholar * Sian Barbosa View author publications You can also search for this author inPubMed Google Scholar *

Felix Lang View author publications You can also search for this author inPubMed Google Scholar * Artur Widera View author publications You can also search for this author inPubMed Google

Scholar CONTRIBUTIONS A.W. conceived and supervised the research. J.K. took and analyzed the experimental data and calculated the theoretical estimations. S.B. and F.L. helped run the

experimental apparatus and collect data. All authors contributed to the interpretation of the data, writing of the manuscript, and critical feedback. CORRESPONDING AUTHOR Correspondence to

Artur Widera. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks the anonymous reviewers

for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional

claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed

under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate

credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article

are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Koch, J., Barbosa, S., Lang, F. _et al._ Stability and sensitivity

of interacting fermionic superfluids to quenched disorder. _Nat Commun_ 15, 9292 (2024). https://doi.org/10.1038/s41467-024-51903-8 Download citation * Received: 29 February 2024 * Accepted:

20 August 2024 * Published: 28 October 2024 * DOI: https://doi.org/10.1038/s41467-024-51903-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative