Reducing herbivory in mixed planting by genomic prediction of neighbor effects in the field
- Select a language for the TTS:
- UK English Female
- UK English Male
- US English Female
- US English Male
- Australian Female
- Australian Male
- Language selected: (auto detect) - EN
Play all audios:

ABSTRACT Genetically diverse populations can increase plant resistance to natural enemies. Yet, beneficial genotype pairs remain elusive due to the occurrence of positive or negative effects
of mixed planting on plant resistance, respectively called associational resistance or susceptibility. Here, we identify key genotype pairs responsible for associational resistance to
herbivory using the genome-wide polymorphism data of the plant species _Arabidopsis thaliana_. To quantify neighbor interactions among 199 genotypes grown in a randomized block design, we
employ a genome-wide association method named “Neighbor GWAS” and genomic prediction inspired by the Ising model of magnetics. These analyses predict that 823 of the 19,701 candidate pairs
can reduce herbivory in mixed planting. We planted three pairs with the predicted effects in mixtures and monocultures, and detected 18–30% reductions in herbivore damage in the mixed
planting treatment. Our study shows the power of genomic prediction to assemble genotype mixtures with positive biodiversity effects. SIMILAR CONTENT BEING VIEWED BY OTHERS NEIGHBOR GWAS:
INCORPORATING NEIGHBOR GENOTYPIC IDENTITY INTO GENOME-WIDE ASSOCIATION STUDIES OF FIELD HERBIVORY Article Open access 29 January 2021 EFFICIENT GENOMICS_-_BASED ‘END_-_TO_-_END’ SELECTIVE
TREE BREEDING FRAMEWORK Article Open access 03 January 2024 INCORPORATING SPATIAL AND GENETIC COMPETITION INTO BREEDING PIPELINES WITH THE R PACKAGE GENCOMP Article 16 January 2025
INTRODUCTION Genetic diversity is increasingly recognized as a critical facet of biodiversity1,2,3 that should be conserved as a provider of various ecosystem services4. In terrestrial
ecosystems, plant genotypic diversity can increase plant resistance to natural enemies as the number of plant genotypes in a contiguous group of plants, namely a stand, increases5,6,7.
However, such a stand of multiple plant genotypes does not always result in positive outcomes8,9,10. Identifying beneficial pairs from a mixture of genotypes helps us design a desirable
mixture that improves stand-level properties, such as resistance to herbivores or pathogens. In anti-herbivore defense, both positive and negative effects of mixed planting on stand-level
resistance have been reported in the literature7,11,12,13. These phenomena are referred to as associational resistance and associational susceptibility, respectively11,14,15. Associational
resistance and susceptibility involve ecological interactions that are mutually non-exclusive, such as plant–herbivore, plant–plant, and plant–carnivore interactions11. In plant-herbivore
interactions, associational resistance or susceptibility occurs when chemical and physical plant traits jointly repel or attract herbivores to neighboring plants14,15,16,17. For instance,
plant odor and apparency may affect the settlement of herbivores17,18,19, while physical barriers and toxic metabolites may alter herbivore behavior and growth after settlement20,21.
Plant–plant interactions may modulate the expression of these plant traits through volatile-mediated communications22 or direct competition23. Plant–carnivore interactions may also lead to
associational resistance or susceptibility when a mixture of plants compared with the component monocultures attracts more or fewer natural enemies of herbivores24,25. The complexity of
associational resistance and susceptibility makes it difficult to distinguish between positively and negatively interacting genotype pairs for anti-herbivore resistance. Nonetheless, the
application of associational resistance to agriculture is becoming more and more important to reduce the use of insecticides17,26. Despite long-standing interest4,27, few studies have
employed genome-wide polymorphism data to investigate stand-level properties in biodiversity research. Other than anti-herbivore resistance, some pioneering studies have used genome-wide
association studies (GWASs) to dissect the genetic basis underlying stand-level growth within the model plant _Arabidopsis thaliana_28,29,30. For example, studies on 98 _A. thaliana_
genotypes have reported quantitative trait loci that mediate neighbor genotype effects on plant growth30 and consequently mitigate belowground competition31. However, these studies require
considerable effort in pairwise cultivation to sufficiently control neighbor composition among many genotypes. Due to this combinatorial cultivation effort, previous studies focused on
limited pairs between ten focal and 98 counterpart genotypes in a controlled environment29,31. These practical limitations remain an obstacle to enabling large-scale GWAS and thereby
identifying the most beneficial pairs in anti-herbivore resistance in field environments. In this study, we aimed to predict key genotype pairs that reduce herbivory by combining genome-wide
single nucleotide polymorphisms (SNPs) in _A. thaliana_32,33 with a recently developed GWAS method named “Neighbor GWAS”34 (Fig. 1). This GWAS method has the same structure as the Ising
model35 of magnetics, which has been applied to various spatial patterns in biology such as cellular development36, animal skin colors37, and forest gap dynamics38. Neighbor GWAS employs
this widely applicable model for spatial variation in quantitative traits to distinguish locus-wise positive or negative interactions between focal and neighbor individuals34 (Fig. 1a).
Neighbor genotype effects estimated by the Neighbor GWAS method determine whether a mixture of two genotypes at a given locus alters phenotypic values at population level (Fig. 1a), thereby
distinguishing SNPs with positive or negative effects. The practical advantage of Neighbor GWAS lies in its applicability to randomized mixtures of many genotypes, providing a suitable
method to analyze how neighbor genotypes shape herbivore damage across space. To apply this method, we first planted replicated individuals of 199 _A. thaliana_ genotypes at two field sites
and observed herbivore damage and naturally emerging communities of herbivores and associated insect species (Fig. 1b), which were analyzed as extended phenotypes of the plants. We then used
Neighbor GWAS as a tool to quantify the phenotypic variation explained by neighbor genotype effects and to conduct GWAS of neighbor genotype effects on herbivore damage and insect community
composition. Genome-wide regression incorporating neighbor genotypes was used for genomic prediction of associational resistance or susceptibility out of all possible 19,701 pairs among the
199 genotypes. To test associational resistance, we finally planted three prospective beneficial pairs in mixtures as well as in monocultures. Our joint study using the recently developed
method and large-scale field experiments identified key genotype pairs responsible for associational anti-herbivore resistance. RESULTS HERBIVORE DAMAGE ON FIELD-GROWN _ARABIDOPSIS THALIANA_
To enable GWAS of herbivore damage, we planted _A. thaliana_ genotypes in a randomized block design in two experimental gardens over two years (Fig. 1 and Supplementary Data 1). This
allowed us to monitor the individual number of 18 insect species on approximately 6400 individual plants (\(\approx\) 199 genotypes \(\times\) 8 blocks \(\times\) 2 sites \(\times\) 2 years)
at a native (Zurich, Switzerland) or exotic (Otsu, Japan) field site (Fig. 2a–d and i–l, Supplementary Fig. 1 and Supplementary Table 1). We quantified herbivore damage as the number of
leaf holes in Zurich and leaf area loss in Otsu because the major herbivores in Zurich were flea beetles, and those in Otsu were caterpillars of diamondback moths or small white butterflies
(Fig. 2b, j and Supplementary Fig. 1). Typically multiple insect species were found on each individual plant (average = 2.1 and 1.8 in Zurich and Otsu, respectively; Fig. 2d, l). The fact
that the major herbivore species observed in our study were specialists of Brassicaceae (Supplementary Fig. 1 and Supplementary Table 1) led us to classify these insects into external
chewers (i.e., herbivores that harbor outside and chew plant tissues) and other herbivores. The former is known to trigger the defense pathways mediated primarily by the plant hormone
jasmonic acid, and the latter includes species that induce defense through salicylic acid39,40,41. To identify the insect functional groups responsible for the herbivore damage, we
quantified three extended phenotypes of insect communities: the individual number of external chewers (flea beetles in Zurich or caterpillars in Otsu), the individual number of other
herbivores (aphids, thrips, stink bugs, and leaf miners), and the total number of insect species per individual plant (Fig. 2b–d and j–l and Supplementary Fig. 2). All four phenotypes
exhibited quantitative phenotypic variation among the individual plants (Fig. 2a–d and i–l), providing suitable target phenotypes for GWAS. Before using the Neighbor GWAS, we performed a
standard GWAS to examine focal genotype effects on herbivore damage and the three extended phenotypes of insect community composition. For all four phenotypes, we found significant
heritability among plant genotypes at both sites (likelihood ratio test, \({\chi }^{2}\) > 19.4, d.f. = 1, \(p\) < 0.01: “focal” in Fig. 2e–h and m–p; Supplementary Fig. 3 and
Supplementary Table 2). Our previous study detected single-gene effects of the trichome developmental gene _GLABRA1_ (_GL1_) on resistance to herbivore damage made by flea beetles42; thus,
two glabrous mutants were included to test this effect. As expected, we detected significant effects of the mutation in the _GL1_ gene on the herbivore damage in Zurich (\(p\) < 0.05
after Bonferroni correction of multiple testing for SNPs; the most significant SNP being located on the third chromosome in Supplementary Fig. 4a and Supplementary Data 2). Although other
studies have reported significant effects of the glucosinolate genes _GS-OH_ and _MAM1_ on herbivory43, none of the measured phenotypes showed significant peaks near these glucosinolate
genes (Supplementary Figs. 4a and 5a and Supplementary Data 2). Presumably, this was because the majority of herbivores observed in this study were specialists (Supplementary Table 1) and
thus overcame the glucosinolate defense. The results of the standard GWAS agreed with previous evidence for physical defense, whereas the herbivore damage observed in our study was unlikely
to be attributable to the known variation in defense due to glucosinolates. GENOME-WIDE NEIGHBOR EFFECTS CONTRIBUTED TO SHAPING HERBIVORE DAMAGE To test whether the observed herbivore damage
was affected by neighbor genotypes, we quantified the phenotypic variation explained (PVE) by neighbor genotypes using the Neighbor GWAS model that considered neighbor genotype effects
besides the focal genotype effects34. This PVE corresponds to heritability attributable to neighbor genotypic effects as well as focal genotype effects34. Compared with focal genotype
effects alone, we found that the inclusion of neighbor genotypes explained a significant fraction of the phenotypic variation in the observed herbivore damage (likelihood ratio test, \({\chi
}^{2}\) > 7.4, d.f. = 1, \(p\) < 0.01; “focal + neig.” in Fig. 2e, m; Supplementary Fig. 3 and Supplementary Table 2). Permutation tests confirmed that the observed fraction of
herbivore damage explained by neighbor genotype effects was greater than that of randomly permuted neighboring plants in Zurich (permutation test, \(p\) < 0.05; Supplementary Fig. 6a and
Supplementary Note 1). This was also supported by a permutation scheme called genome rotation44,45 that randomized population genetic structure (permutation test, \(p\) < 0.05;
Supplementary Fig. 6d and Supplementary Note 1). These results show the importance of neighbor genotypes in shaping herbivore damage in the field. Similarly, we quantified the phenotypic
variation explained by neighbor genotypes for the three extended phenotypes of the insect community composition to examine which types of observed herbivores were the most influenced by
neighbor genotypes. Specifically, we asked whether neighbor genotypes were more likely to influence insect species with higher mobility. The vast majority of external chewers in Zurich were
flea beetles that could jump between plants (‘Ps’ and ‘Pa’ in Supplementary Fig. 1b, d and Supplementary Table 1), and the individual number of external chewers on focal plants was
significantly influenced by neighbor genotypes (likelihood ratio test, \({\chi }^{2}\) = 6.0, d.f. = 1, \(p\) < 0.05; Fig. 2f and Supplementary Table 2). In contrast, the contribution of
neighbor genotypes to the individual number of external chewers on focal plants was not significant in Otsu (Fig. 2n and Supplementary Table 2), where the major external chewers were
sedentary caterpillars that could not move quickly between plants (‘Px’, ‘Pr’, and ‘Ar’ in Supplementary Fig. 1c and e and Supplementary Table 1). In Otsu, instead, flower thrips that could
move between flowering stems (‘Fi’ in Supplementary Fig. 1c and e and Supplementary Table 1) were abundant in the category of other herbivores, and accordingly, the individual number of
other herbivores was significantly influenced by neighbor genotypes (likelihood ratio test, \({\chi }^{2}\) = 5.6, d.f. = 1, \(p\) < 0.05; Fig. 2o and Supplementary Table 2). Consistent
with the significant influence of neighbor genotypes on either external chewers in Zurich or other herbivores in Otsu, the total number of insect species at both sites was affected by
neighbor genotypes (likelihood ratio test, \({\chi }^{2}\) > 4.8, d.f. = 1, \(p\) < 0.05; Fig. 2h, p, Supplementary Fig. 3 and Supplementary Table 2). These patterns of insect
communities suggest that neighbor genotypes are more likely to influence mobile herbivores than sedentary ones. We then conducted GWAS of neighbor genotype effects on the herbivore damage
and the three extended phenotypes of insect communities. To attribute phenotypic variation to each SNP, we mapped the statistical significance of the neighbor genotype effect \({\beta
}_{2}\) on the _A. thaliana_ genome and depicted Manhattan plots (Fig. 3a–d, i–l, Supplementary Figs. 4, 5 and Supplementary Data 2). This GWAS did not detect any significant SNPs for any of
the four phenotypes at each site (\(p\) > 0.1 after Bonferroni correction of multiple testing for SNPs: Fig. 3). This was also supported by permutation tests that shuffled neighboring
plants and by the genome rotation scheme (\(p\) > 0.1; Supplementary Fig. 6b, c, e, f and Supplementary Note 1). Together with the significant PVE by neighbor genotype effects (Fig. 2e–h,
m–p), these results suggest a heritable but polygenic basis for neighbor effects on the herbivore damage and insect community composition. In the Neighbor GWAS, the sign of the estimated
neighbor genotype effects \({\hat{\beta }}_{2}\) represents positive or negative interactions between the two alleles of paired neighbors, which corresponds to associational resistance or
susceptibility to herbivore damage and insect community composition34,46 (upper right inset in Fig. 1a and Supplementary Fig. 7c–f). We therefore examined the number and frequency of SNPs
with positive or negative \({\hat{\beta }}_{2}\) separately for the four phenotypes per site. We detected both negative and positive \({\hat{\beta }}_{2}\) in the top 0.1%-associated SNPs
(histograms in Fig. 3e–h, m–p and Supplementary Fig. 8a–h). The SNPs with associational resistance (\({\hat{\beta }}_{2} > 0\)) involved more minor alleles than those with associational
susceptibility (\({\hat{\beta }}_{2} < 0\)) in five out of the four phenotypes \(\times\) two sites (boxplots in Fig. 3e–h, m–p, Supplementary Fig. 8i–p and Supplementary Table 3),
including the herbivore damage in Zurich (Fig. 3e). These data suggest that associational resistance may be less frequent than associational susceptibility among the _A. thaliana_ genotypes.
This frequency bias further motivated us to analyze another possible difference between the SNPs with positive and negative \({\hat{\beta }}_{2}\), such as patterns of selection scanned by
using genome-wide polymorphism data. This selection scan revealed that SNPs with associational resistance (\({\hat{\beta }}_{2} > 0\)) had more signatures of balancing selection than
those with associational susceptibility (\({\hat{\beta }}_{2} < 0\)) (Supplementary Fig. 9 and Supplementary Note 2). These results highlight the different features of the top-scoring
SNPs with associational resistance and susceptibility. Among many possible SNPs, we then attempted to determine key predictors that explain herbivore damage or insect community composition.
GENOMIC PREDICTION AND VALIDATION OF KEY GENOTYPE PAIRS IN THE FIELD Due to the lack of significant SNPs associated with the neighbor effects, it was not feasible to predict key genotype
pairs based on a few SNP predictors. We solved this problem using a genomic prediction approach47 that incorporated genome-wide SNPs for phenotype prediction. To predict the neighbor
effects, we included all 1.2 million SNPs representing focal genotypes and neighbor genotypes in the least absolute shrinking and selection operator (LASSO)48. With or without neighbor
genotypes, LASSO prediction was validated using a test dataset collected in an additional year (see “Methods”). Among the four phenotypes we had measured per site, the test dataset of
herbivore damage in Zurich was slightly better explained by the neighbor-including LASSO than by the neighbor-excluding LASSO (Spearman’s \(\rho\) = 0.416 and 0.391 for neighbor-including
and neighbor-excluding LASSO, respectively: Supplementary Fig. 10). This result indicates that the herbivore damage in Zurich can be better predicted by incorporating neighbor genotypes.
Therefore, we extracted 756 neighbor-related SNPs using the neighbor-including LASSO that better predicted the herbivore damage in Zurich (Supplementary Fig. 11a, b). To understand the
potential mechanisms behind the 756 SNP predictors of the herbivore damage in Zurich, we performed gene ontology enrichment analyses for candidate genes relevant to associational resistance
(the LASSO-selected SNPs with \({\hat{\beta }}_{2} > 0\)) or associational susceptibility (\({\hat{\beta }}_{2} < 0\)) (Supplementary Data 3). For the candidate genes of associational
resistance, we detected a significant enrichment of gene ontology with ‘jasmonic acid biosynthetic process’ (false discovery rate < 0.05; Supplementary Data 4), including the
_LIPOXIGENASE2_ (_LOX2_) and _LOX6_ genes (chr3-16519704 with MAF = 0.40 near _LOX2_; chr1-25316686 with MAF = 0.44 and chr1-25317359 with MAF = 0.44 near _LOX6_; Supplementary Data 3).
_LOX2_ is particularly known as an essential gene for the production of volatiles49, which can reduce herbivory on neighboring plants50. In contrast, jasmonate-related gene ontology was not
enriched in the candidate genes relevant to associational susceptibility (Supplementary Data 4). These results suggest the potential relevance of jasmonate-mediated defense in associational
resistance to herbivore damage, motivating us to predict beneficial pairs using the set of SNPs selected by LASSO. Using neighbor genotypes as a better predictor, we attempted to predict
associational resistance or susceptibility to herbivore damage in Zurich. To this end, we extrapolated the 756 LASSO-selected SNPs to virtual mixture (a pair of two different genotypes) or
monoculture (a pair of the same genotypes) conditions in silico (Supplementary Fig. 11c). We estimated the relative effects of two-genotype mixtures on herbivore damage (Fig. 4a,
Supplementary Fig. 11d, e and Supplementary Note 3). Consistent with the higher frequencies of SNPs with associational susceptibility than associational resistance in GWAS (Fig. 3e), the
pairwise effect size had a negative mode of distribution (Fig. 4a). Susceptible plant genotypes under monoculture imposed more damage on their counterparts when planted with another
genotype, which was suggested by the negative correlation between the pairwise effect size and estimated herbivore damage under monoculture (Spearman’s \(\rho\) = – 0.38; test for no
correlation, \(p\) = 3.4E-08: Fig. 4b). In addition, based on the pairwise effect size of mixed planting (Fig. 4a), our simulations confirmed that herbivore damage increased when the number
of genotypes increased (Fig. 4c; Supplementary Fig. 11f; see “Methods”). These results suggest the prevalence of associational susceptibility to herbivore damage in Zurich among the 199
genotypes. In this situation, we asked whether identifying beneficial pairs would be feasible. Despite the prevalence of negatively interacting pairs (< 0 in Fig. 4a), 823 pairs had a
positive estimate for mixed planting (> 0 in Fig. 4a). To verify associational resistance at the stand level in situ, we planted three genotype pairs under monoculture and mixture
conditions at the Zurich site (Supplementary Fig. 12). We tested Bg-2 and Uod-1 as a pair with a large positive effect; Vastervik and Jm-0 as a pair with a moderate positive effect; and
Bro1-6 and Bla-1 as a pair with a slightly positive effect from the range of positive effect sizes (Fig. 4a; see “Methods”). Consistent with this order of effect size, the pair of Bg-2 and
Uod-1 indeed showed a significant reduction (average of 24.8% within a pair; Supplementary Table 4b) in herbivore damage in the mixtures in the field (marginal means of the herbivore damage,
\(t\) > 2.02, d.f. = 125, adjusted \(p\) < 0.05; Fig. 4d and Supplementary Tables 4, 5). The pair of Vastervik and Jm-0 also showed a significant reduction (average of 22.7% within a
pair) in herbivore damage in the mixture compared with the average monocultures (marginal means of herbivore damage, \(t\) > 2.22, d.f. = 125, adjusted \(p\) < 0.05; Fig. 4d and
Supplementary Tables 4, 5). Expected from their smallest effect size, the pair of Bla-1 and Bro1-6 did not show a significant reduction in herbivore damage in the mixtures (Fig. 4d and
Supplementary Tables 4, 5). Next, we conducted laboratory choice experiments in which black flea beetles were allowed to feed on the mixture of each of the three pairs. This experiment found
significant differences in herbivore damage between Bg-2 and Uod-1 (likelihood ratio test, \({\chi }^{2}\) = 13.35, d.f. = 1, \(p\) < 0.001); and between Vastervik and Jm-0 (\({\chi
}^{2}\) = 5.71, d.f. = 1, \(p\) < 0.05); but not between Bla-1 and Bro1-6 (\({\chi }^{2}\) = 0.87, d.f. = 1, \(p\) = 0.35; Supplementary Fig. 13 and Supplementary Table 6), in agreement
with observed effects of the field experiments. Taken together, field experiments and laboratory evidence demonstrated that candidate genotype pairs underpinned associational resistance to
herbivory. DISCUSSION In this study, we successfully predicted key genotype pairs that underpin associational resistance from numerous combinations of genotypes in which associational
susceptibility was by far more prevalent. Intraspecific associational susceptibility to specialist herbivores is ubiquitous across plant species, as suggested by a previous meta-analysis
that reported the prevalence of negative effects of plant genotypic diversity on resistance to specialist herbivores9. The present work overcame the difficulty in distinguishing
associational resistance from associational susceptibility by leveraging genome-wide polymorphism data. Other than anti-herbivore resistance, recent genome-wide studies have identified key
genotype pairs that increase stand-level growth based on the limited number of genotype pairs in a controlled environment29,31. In contrast to this previous work, our approach can be applied
to randomized mixtures of many genotypes over a large space in the field. Such applicability to large-scale field experiments provides a novel solution to ecologically relevant genetics and
the prediction of intraspecific biodiversity effects on various traits of interest. Genomic prediction enabled us to identify key genotype pairs even though no significant SNPs were
detected by GWAS. This strategy is comparable to genomic selection in plant breeding, in which elite genotypes can be selected without identifying genes responsible for a heritable
phenotype51,52,53. Identification of elite genotypes is successful when genome-wide polymorphisms are sufficiently dense to represent the genetic potential of each genotype51. Prediction of
genetic potential is often achieved using LASSO and its varieties52. Combining LASSO and Neighbor GWAS, our study expanded the concept of genomic selection towards neighbor genotype effects
and thereby showed the power of genome-wide polymorphism data to predict elite genotype pairs. Associational resistance can occur through ecological interactions that are mutually
non-exclusive, such as plant–herbivore, plant–plant, and plant–carnivore interactions. Although elucidation of the detailed mechanisms is not the goal of genomic prediction, our genome-wide
analysis provides insights into the potential mechanisms of associational resistance. For instance, key SNPs near _LOX_s suggest a potential relationship between jasmonate-induced defense
and associational resistance to flea beetles, as _LOX_ genes alter volatile production through jasmonic-acid pathways49,50. Such volatile chemicals are known to play three multifunctional
roles in associational resistance by repelling herbivores away from neighboring plants19, eliciting defense responses in neighboring plants22, and attracting carnivorous insects25. In our
study system, carnivore-mediated interactions are unlikely to explain associational resistance because specialist predators or parasitoids have not been observed for flea beetles. This
observation suggests that volatile-mediated mechanisms allowing herbivore repellency or direct plant–plant communication could be two of the three ecological interactions in our study
system. The complex genomic basis of neighbor effects remains, however, as a challenge in elucidating the mechanisms of associational resistance. Manipulating multiple genes54 is ultimately
needed to verify the set of small-effect genes responsible for quantitative variation in herbivore damage. To this end, our genome-wide study paves the way to identify candidate genes for
further genetic studies. Our study highlights the importance of field data of the model species _A. thaliana_ in investigating ecological interactions under naturally fluctuating
conditions42,55,56,57,58. Based on detailed field surveys of the insect community, we found that some herbivore species were influenced by neighboring plant genotypes while others were not.
Specifically, we detected a significant influence of neighbor genotypes on jumping flea beetles but not on sedentary caterpillars. The initial occurrence of caterpillars could be determined
through oviposition by mobile adult females to some extent, but long-lived plant species would be suitable to observe the process in which these caterpillars become mature and disperse again
onto neighboring plants. When our method is applied to long-lived plants, it may enable us to predict the impacts of intraspecific mixed planting on more diverse herbivores at the community
level. Intraspecific mixed planting, also known as variety mixture, is of considerable interest in pest management to reduce the use of agricultural chemicals such as insecticides26,29,59.
Targeting key genotype pairs may help us design resistant mixtures without complicating agronomic management. For instance, cultivars can be easily harvested when flowering time synchronizes
between varieties within a plant species59. The genotypes of our key pair Bg-2 / Uod-1 are known to have similar flowering times (46.2 days for Bg-2 and 45.6 days for Uod-1 under a long-day
condition)60. This fact indicates that we have achieved a resistant genotype mixture without differentiating plant life history. This novel strategy to identify genotype pairs with
beneficial mixture effects may be more widely applicable to genotype mixtures in crops and other plantations. METHODS FIELD GWAS EXPERIMENTS PLANT GENOTYPES We used _A. thaliana_ genotypes
that were selfed and maintained as inbred lines, called “accessions.” To study the genomic variation responsible for biotic interactions, we overlapped our accessions with those used in the
GWAS of microbial communities61 and glucosinolates62. We used 199 accessions with a few additional accessions (Supplementary Table 1), all of which were genotyped in the RegMap32 and 1001
Genomes33 projects. Seeds of these accessions were obtained from the Arabidopsis Biological Resource Center (https://abrc.osu.edu/). The Santa-Clara accession was replaced with Fja1-1 in
2018 because the genotype of Santa-Clara was unavailable. For the genotype data, we downloaded a full imputed SNP matrix of 2029 accessions from the AraGWAS Catalog63. Of the full 10,709,466
SNPs, we used 1,819,577 SNPs with minor allele frequency (MAF) > 0.05. L_er_(_gl1-1_) and Col(_gl1-2_) were included as positive controls to test the known single-gene effects of
_GLABRA1_ (_GL1_) on flea beetle resistance42. The L_er_ or Col genome was assigned to the two _gl1_ mutants, with only the _GL1_ locus differing between the parental wild-type and _gl1_
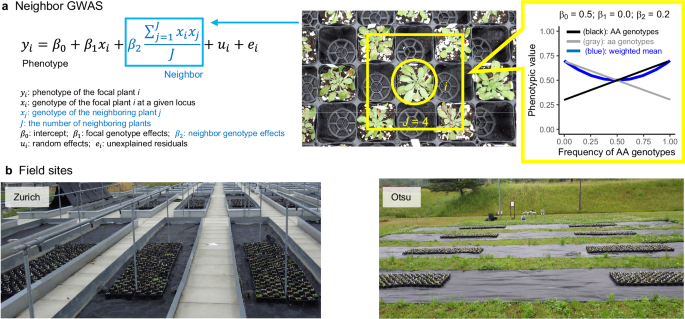
mutants. FIELD SETTING To investigate the two distinct herbivore communities, we used field sites within or outside the natural distribution range of _A. thaliana_. As a native site, we used
the outdoor garden of the University of Zurich-Irchel campus (Zurich, Switzerland: 47 °23’N, 8 °33’E, alt. ca. 500 m) (Fig. 1b). As an exotic site, we used the Center for Ecological
Research, Kyoto University (Otsu, Japan: 35 °06’N, 134 °56’E, alt. ca. 200 m) (Fig. 1b). In the Otsu site, weeds were mown before the experiment, and the surroundings were covered with
agricultural sheets before the experiment (Fig. 1b). In the Zurich site, each experimental block was placed in a separate bed (Fig. 1b) that was not accessible to molluscan herbivores. The
field experiment at Otsu was conducted from late May to mid-June, and that at Zurich was conducted from late June to mid-July. The exact date of the field survey is annotated on the original
data file64. Plants were initially grown under controlled conditions and then planted in a field garden for three weeks. Seeds were sown on Jiffy-seven pots (33-mm diameter), and stratified
under 4 °C for a week. Seedlings were cultivated for 1.5 months under a short-day condition (8 h light: 16 h dark, 20 °C). Plants were then separately potted in plastic pots (6 cm in
diameter) filled with mixed soil of agricultural composts (Profi Substrat Classic CL ED73, Einheitserde Co. in Zurich; Metro-mix 350, SunGro Co., USA in Otsu) and perlites at a 3:1 L ratio.
The potted plants were covered with agricultural shading nets and acclimated to field conditions for a few days. A set of the 199 accessions and an additional Col-0 accession — namely, 200
individuals in total — was randomly assigned to each block without replacement and positioned in a checkered manner (Fig. 1a). Eight blocks of the 200 accessions were set at each site on
2017 and 2018 for GWAS. Three blocks of the 200 accessions were set at each site in 2019 for the model validation of LASSO (see “Modified Neighbor GWAS for LASSO” below). The blocks were
> 2.0 m apart. PHENOTYPE SURVEY Insects and herbivorous collembola on individual plants were visually counted every 2–3 days. These species were identified using a magnifying glass.
Dwelling traces and mummified aphids were also counted as proxies for the individual number of leaf miners and parasitoid wasps, respectively. Eggs, larvae, and adults were counted for all
species, as long as they could be observed by the naked eye. All counts were performed by a single observer (Y. Sato) during the daytime at each site. At the Zurich site, yellow-striped and
black flea beetles occurred every year (at least for four years42,65). Small holes made by these flea beetles were counted at the Zurich site and their maximum number throughout the
experiment was used as an indicator of herbivore damage. This phenotyping was not applicable to Otsu, because the most abundant herbivores were not flea beetles34. Instead, the percentage of
leaf area loss was scored in Otsu at the end of the experiment as follows: 0 for no visible damage, 1 for < 10%, 2 for > 10% and < 25%, 3 for > 25% and < 50%, 4 for > 50%
and < 75%, and 5 for > 75% of area eaten. We also recorded the initial plant size and presence/absence of inflorescences to incorporate these phenotypes as covariates in the
statistical analyses. Initial plant size was evaluated by the length of the largest rosette leaf (mm) at the beginning of the field experiment because this parameter represents the plant
size at the growth stage. The presence or absence of inflorescences was recorded 2 weeks after transplantation. Herbivore damage was evaluated by the number of leaf holes in Zurich and the
leaf area loss in Otsu, as described above. The maximum number of individuals in each experiment was used as an index for the abundance of each insect species. In our dataset, we defined
extended plant phenotypes that represent insect community composition based on herbivore feeding habits and species richness. The insect community composition more significantly differed
between the two sites than between 2017 and 2018 (redundancy analysis, \(F\) = 401, \(p\) < 0.001 for the sites; \(F\) = 152, \(p\) < 0.001 for the years: Supplementary Fig. 1a); thus,
the dataset was separated into Zurich and Otsu. The individual number of external chewers or other herbivores was defined as the total number of individuals of leaf-chewing species (e.g.,
beetles and caterpillars) or species that ate internal parts of a plant (e.g., phloem-sucking aphids, cell-content-sucking thrips, sap-sucking stink bugs, and leaf miners). The reason for
this classification was to reflect the difference in plant defense responses to external chewers and other herbivores through jasmonic acid and salicylic acid pathways, respectively39,40,41.
Leaf miners are known as endophagous herbivore66 that can elicit both the jasmonic and salicylic acid pathways in plant defense responses41. Based on their relevance to plant defense
responses mediated by the salicylic acid pathway, leaf miners were included in the category of other herbivores. The individual number of other herbivores, to a large extent, represented the
individual number of sap-sucking herbivores (i.e., phloem-sucking aphids, cell content-sucking thrips, and sap-sucking stink bugs) because leaf miners were very rare (0.35% of all
individuals in the other herbivore category; see the raw data64). Specialist–generalist classification was not applicable to our dataset because generalist herbivores were much fewer than
specialist herbivores at both sites (Supplementary Fig. 1; Supplementary Table 2). Herbivore–carnivore ratio was also not applicable because carnivorous insects (e.g., parasitoid wasps and
aphidophagous ladybirds) were much fewer than herbivores. These carnivorous insects were taken into consideration to calculate insect species diversity. For the index of insect species
diversity, we calculated the exponential Shannon diversity and Simpson diversity indices in addition to the total number of insect species i.e., species richness. However, Shannon diversity
and Simpson diversity showed a bimodal distribution that did not suit GWAS, and only the total number of insect species had quantitative phenotypic values (Supplementary Fig. 2). We,
therefore, used the total number of insect species as an index of the insect species diversity. The insect community composition was analyzed using the vegan package v2.6-467 in R. All
phenotypes except for the leaf area loss (score variable) were ln(\(x\)+ 1)-transformed to improve normality for GWAS and genomic prediction. Unless otherwise stated, all statistical tests
were two-sided and all figure presentations and basic statistical analyses were performed using R version 3.6.1 or above68. GWAS WITH FOCAL AND NEIGHBOR GENOTYPE EFFECTS NEIGHBOR GWAS MODEL
To separate the effects of focal and neighbor genotype effects on herbivore damage and insect community composition, we used the Neighbor GWAS model developed by Sato et al. (2021)34.
Neighbor GWAS employs a linear mixed model that includes additional fixed and random effect34. According to the same mixed model as Eq. 2 of Sato et al.34, we present a specific case that
fits the data structure of the present field experiments as follows. Let \({x}_{i}\) and \({x}_{j}\) be the allelic status at each SNP of the \(i\)-th focal plant and \(j\)-th neighboring
plant, respectively. The inbred accessions had two states as \({x}_{i}\in\) {– 1, + 1}. A phenotype value of the \(i\)-th focal individual plant \({y}_{i}\) was then given as
$${y}_{i}={\beta }_{0}+{\beta }_{1}{x}_{i}+{\beta }_{2}\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J+{u}_{i}+{e}_{i}$$ (1) where \({\beta }_{0}\) is the intercept; \({\beta }_{1}{x}_{i}\)
is a fixed effect of the focal genotype and the same as standard GWAS, and the second coefficient \({\beta }_{2}\) determines positive or negative effects from the mean allelic similarity
\(\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J\) at a given locus between the focal individual \(i\) and neighboring individuals \(j\) up to the total number of neighboring individuals
\(J\). When the focal plant shares the same allele with a neighboring plant, the product \({x}_{i}{x}_{j}\) = (– 1)\(\times\)(– 1) = + 1 or (+ 1)\(\times\)(+ 1) = + 1. By contrast, when a
neighboring plant has a different allele from the focal plant, the product \({x}_{i}{x}_{j}\) = (– 1)\(\times\)(+ 1) = – 1 or (+ 1)\(\times\)(– 1) = – 1. The average of these products
represents the mean allelic similarity of the focal plant with neighboring plants \(\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J\) (\(J\) representing the number of neighboring plants
\(L\) in the linear mixed model Eq. 2 of Sato et al.34). The coefficient \({\beta }_{2}\) then determines the direction and strength of the effects of neighbor genotype similarity on a
phenotype. In addition to the fixed effects, the random effects \({u}_{i}\) and residuals \({e}_{i}\) contribute to phenotypic variation. These random effects and residuals follow a normal
distribution as \({u}_{i}\sim N\left({{{\bf{0}}}},{\sigma }_{1}^{2}{{{{\bf{K}}}}}_{1}+{\sigma }_{2}^{2}{{{{\bf{K}}}}}_{2}\right)\) and \({e}_{i}\sim N\left(0,{\sigma }_{e}^{2}\right)\) (‘~’
meaning ‘distributed as’: see also page 3 in Sato et al.34). The variance component parameters \({\sigma }_{1}^{2}\) and \({\sigma }_{2}^{2}\) represent the polygenic effects of focal and
neighbor genotypes on a phenotype, respectively. Same as the standard GWAS69, \({{{{\bf{K}}}}}_{1}\) represents a kinship matrix among \(n\) plants and is defined as the fraction of shared
alleles among all SNP sites for a pair of accessions. \({{{{\bf{K}}}}}_{2}\) represents a sample structure due to additive effects of neighbor genotypes among \(n\) plants given by the
cross-product \({{{{\bf{K}}}}}_{2}={{{{\bf{X}}}}}_{2}^{T}{{{{\bf{X}}}}}_{2}/\left(q-1\right)\) (see page 3, “Variation partitioning” in Sato et al.34). The elements of \({{{{\bf{X}}}}}_{2}\)
include covariates of the neighbor genotype similarity34. With all the elemental covariates shown, the \(q\)-SNPs \(\times\) \(n\)-plants matrix \({{{{\bf{X}}}}}_{2}\) can be expressed as
follows: $${{{{\bf{X}}}}}_{2}=\left(\begin{array}{cccc}\left({\sum }_{j=1}^{J}{x}_{1,1}\, {x}_{j}\right)/J & \left({\sum }_{j=1}^{J}{x}_{1,2}\, {x}_{j}\right)/J & ... &
\left({\sum }_{j=1}^{J}{x}_{1,n}\, {x}_{j}\right)/J\\ \left({\sum }_{j=1}^{J}{x}_{1,2}\, {x}_{j}\right)/J & \left({\sum }_{j=1}^{J}{x}_{2,2}\, {x}_{j}\right)/J & ... &
\left({\sum }_{j=1}^{J}{x}_{2,n}\, {x}_{j}\right)/J\\ ... & ... & ... & ...\\ \left({\sum }_{j=1}^{J}{x}_{q,1}\, {x}_{j}\right)/J & \left({\sum }_{j=1}^{J}{x}_{q,2}\,
{x}_{j}\right)/J & ... & \left({\sum }_{j=1}^{J}{x}_{q,n}\, {x}_{j}\right)/J\\ & & & \end{array}\right)$$ PHENOTYPIC VALUES UNDER MONOCULTURE OR MIXTURE The core idea of
the Neighbor GWAS method was inspired by the Ising model of ferromagnetism to estimate its interaction coefficient based on the genotypic similarity between neighboring individuals34. In
this paragraph, we briefly describe the major points (see pages 2–3 and Fig. 1 in Sato et al. for details34). To recapture the similarity between the Ising model and Neighbor GWAS, we
focused on the fixed effects of Eq. 1 without the intercept \({\beta }_{0}\), the random effects \({u}_{i}\) and residuals \({e}_{i}\) as \({y}_{i}={\beta }_{1}{x}_{i}+{\beta
}_{2}\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J\). When we sum up the phenotype values for the total number of plants \(n\) and replaced it as \(E=-{\beta }_{2}\), \(H=-{\beta }_{1}\)
and \({\epsilon }_{I}=\sum {y}_{i}\), Eq. 1 can be transformed as \({\epsilon }_{I}=-E{\sum }_{ < i,j > }{x}_{j}{x}_{j}-H\sum {x}_{i}\), which represents the interaction energy of the
Ising model. The neighbor genotype effect \({\beta }_{2}\) and focal genotypic effect \({\beta }_{1}\) can be interpreted as the energy coefficient \(E\) and the external magnetic effect
\(H\), respectively. In this analogy, an individual plant represents a magnet whose north or south dipole corresponds to two homozygotes at each locus. When simulating the spatial
arrangement of individual plants, the negative and positive \({\beta }_{2}\) determine whether clustering or mixing patterns decrease the total energy \({\epsilon }_{I}=\sum {y}_{i}\)
(Supplementary Fig. 7a, b). The analogy of the Ising model suggests that the different signs of \({\beta }_{2}\) modulate phenotypic values under monoculture or a mixture of the two
genotypes at a given locus. Increased or decreased phenotypic values under genotype mixtures can be shown by assuming random interactions among neighboring plants46. Based on this
assumption, we can provide a simplified case of two inbred genotypes for the general model of frequency-dependent selection46,70 and thereby clarify the relationships between mean phenotype
values and genotype frequencies in a neighborhood (upper right inset of Fig. 1a). In particular, the diploid inbred case in Sato et al.46 represents the present case of _A. thaliana_
accessions. To showcase this, we consider the mean trend of Eq. 1 without the random effects \({u}_{i}\) and residuals \({e}_{i}\) below. Let \({f}_{{{{\rm{AA}}}}}\) and
\({f}_{{{{\rm{aa}}}}}\) be the frequencies of AA and aa genotypes within a population, where \({f}_{{{{\rm{AA}}}}}+{f}_{{{{\rm{aa}}}}}=1\). Then Eq. S13a and b of Sato et al.46 define the
phenotype value for the AA or aa genotype as: $${y}_{{{{\rm{AA}}}}} ={\beta }_{0}+{\beta }_{1}+{\beta }_{2}\left(2{f}_{{{{\rm{AA}}}}}-1\right)\\ {y}_{{{{\rm{aa}}}}} ={\beta }_{0}-{\beta
}_{1}-{\beta }_{2}\left(2{f}_{{{{\rm{AA}}}}}-1\right)$$ and the weighted mean of the two phenotype values \({y}_{{{{\rm{AA}}}}}\) and \({y}_{{{{\rm{aa}}}}}\) can be given by Eq. S14 of Sato
et al.46 as: $$\bar{y} ={{f}_{{{{\rm{AA}}}}}y}_{{{{\rm{AA}}}}} \,+\, \left(1-{f}_{{{{\rm{AA}}}}}\right){y}_{{aa}}\\ ={\beta }_{2}{({2f}_{{{{\rm{AA}}}}}-1)}^{2} \,+\, {\beta
}_{1}\left({2f}_{{{{\rm{AA}}}}}-1\right)+{\beta }_{0}$$ In this set of three equations, the sign of the neighbor genotype effect \({\beta }_{2} > 0\) and \({\beta }_{2} < 0\)
determines the convexness and concaveness of the weighted mean \(\bar{y}\) in response to the genotype frequency \({f}_{{{{\rm{AA}}}}}\), respectively (upper right inset of Fig. 1a and
Supplementary Fig. 7c, d). This analysis led us to focus on SNPs with \({\hat{\beta }}_{2} > 0\) with the aim of reducing herbivore damage by mixed planting (Fig. 1a). PHENOTYPIC
VARIATION EXPLAINED BY FOCAL AND NEIGHBOR GENOTYPE EFFECTS Using the Neighbor GWAS model (Eq. 1), we quantified the proportion of the phenotypic variation explained (PVE) by focal and
neighbor genotype effects for each phenotype. The individual-level equation (Eq. 1) can be expressed as a conventional matrix form, which is the same as Eq. 3 of Sato et al.34, as follows:
$${{{\bf{y}}}}={{{\bf{X}}}}\vec{\beta }+{{{\bf{Zu}}}}+{{{\bf{e}}}}$$ (2) where \({{{\bf{y}}}}\) is \(n\times 1\) vector of phenotypes; \({{{\bf{X}}}}\) includes mean, focal genotype values
\({x}_{i}\), neighbor genotype similarity \(\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J\) and other confounding covariates as a matrix of fixed effects for \(n\) plants; \(\vec{\beta }\)
is a vector that represents coefficients of the fixed effects; \({{{\bf{Z}}}}\) is a design matrix that assigns individuals to a genotype, and becomes an identity matrix if all plants have
different genotypes; \({{{\bf{u}}}}\) is the random effect with Var(\({{{\bf{u}}}}\)) \(={\sigma }_{1}^{2}{{{{\bf{K}}}}}_{1}+{\sigma }_{2}^{2}{{{{\bf{K}}}}}_{2}\); and \({{{\bf{e}}}}\) is
residual as Var(\({{{\bf{e}}}}\)) \(={\sigma }_{e}^{2}{{{\bf{I}}}}\). We estimated \({\hat{\sigma }}_{1}^{2}\) and \({\hat{\sigma }}_{2}^{2}\) (‘hat’ meaning estimates) using Eq. 2, and
calculated PVE by Neighbor GWAS model as PVE = \(\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma }}_{2}^{2}\right)/\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma }}_{2}^{2}+{\hat{\sigma
}}_{e}^{2}\right)\). When \({\beta }_{2}\) and \({\sigma }_{2}^{2}\) are set to 0, the Neighbor GWAS model (Eq. 1) is equivalent to the standard GWAS model \({y}_{i}={\beta }_{0}+{\beta
}_{1}{x}_{i}+{u}_{i}+{e}_{i}\) or \({{{\bf{y}}}}={{{\bf{X}}}}\vec{\beta }+{{{\bf{Zu}}}}+{{{\bf{e}}}}\), where Var(\({{{\bf{u}}}}\)) \(={\sigma }_{1}^{2}{{{{\bf{K}}}}}_{1}\) (see page 4 of
Sato et al.34). We used this standard GWAS model to quantify SNP heritability as \({h}^{2}={\sigma }_{1}^{2}/\left({\sigma }_{1}^{2}+{\sigma }_{e}^{2}\right)\), where \({h}^{2}\) was
equivalent to the single PVEself defined by Sato et al.34. Because focal genotype values \({x}_{i}\) and neighbor genotypic similarity \(\left({\sum }_{j=1}^{J}{x}_{i}{x}_{j}\right)/J\) are
correlated each other (Supplementary Fig. 14 and Supplementary Note 4), it was difficult to separate the focal and neighbor genotype effects as \({\hat{\sigma }}_{1}^{2}/\left({\hat{\sigma
}}_{1}^{2}+{\hat{\sigma }}_{2}^{2}+{\hat{\sigma }}_{e}^{2}\right)\) and \({\hat{\sigma }}_{2}^{2}/\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma }}_{2}^{2}+{\hat{\sigma }}_{e}^{2}\right)\)34
(see also the page 4 and Fig. 3 in Sato et al.34). Instead, the net contribution of neighbor genotype effects to a phenotype can be sufficiently evaluated as PVE – \({h}^{2}\), which is
equivalent to the net PVEnei of Sato et al.34 (Supplementary Fig. 15 and Supplementary Note 4). To avoid confounding focal and neighbor genotype effects, PVE should be tested from simpler to
complex models. This stepwise procedure for the likelihood ratio tests was established in our previous study (see page 6 in Sato et al.34), as follows: * 1. Compute the null likelihood with
\({\sigma }_{1}^{2}=0\) and \({\sigma }_{2}^{2}=0\). * 2. Compare models with and without \({\sigma }_{1}^{2}\) based on the likelihood ratio test for \({\sigma }_{1}^{2}\). * 3. Calculate
\({h}^{2}={\hat{\sigma }}_{1}^{2}/\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma }}_{e}^{2}\right)\). * 4. Compute the likelihood with \({\sigma }_{1}^{2}\ne 0\) and \({\sigma }_{2}^{2}=0\). *
5. Compare models with and without \({\sigma }_{2}^{2}\) based on the likelihood ratio test for \({\sigma }_{2}^{2}\). * 6. Calculate PVE = \(\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma
}}_{2}^{2}\right)/\left({\hat{\sigma }}_{1}^{2}+{\hat{\sigma }}_{2}^{2}+{\hat{\sigma }}_{e}^{2}\right)\). This procedure was performed using the rNeighborGWAS package v1.2.434, where linear
mixed models were solved using the average information-restricted maximum likelihood method implemented in the gaston package v1.5.571. The statistical significance of the PVE was determined
using the likelihood ratio between a simpler and complex model, which asymptotically follows a \({\chi }^{2}\) distribution with one degree of freedom. Multiple testing was not considered
among phenotypes as it was not common in PVE analyses and GWAS of multiple phenotypes30,60,61. The initial plant size, presence/absence of inflorescences, study years, and differences in
experimental blocks were considered non-genetic covariates. To empirically test the significance of PVE, we also performed a permutation test in which neighboring plants within blocks or
genomic positions were randomized (Supplementary Fig. 6 and Supplementary Note 1). GENOME-WIDE ASSOCIATION STUDY (GWAS) We tested the focal or neighbor genotype effects \({\beta }_{1}\) or
\({\beta }_{2}\) for all SNPs to conduct GWAS. Similar to the PVE test, the likelihood ratio test was performed from simpler to complex models. The stepwise likelihood ratio test was
established in our previous study (see page 6 in Sato et al.34), as follows: * 1. Compute the null likelihood with \({\sigma }_{1}^{2}\ne 0\) and \({\sigma }_{2}^{2}=0\). * 2. Test the focal
genotypic effect \({\beta }_{1}\) in comparison with the null likelihood. * 3. Compute the focal likelihood with \({\hat{\sigma }}_{1}^{2}\), \({\hat{\sigma }}_{2}^{2}\), and \({\beta
}_{1}\). * 4. Test the neighbor genotype effects \({\beta }_{2}\) in comparison with the focal likelihood. This line of GWAS analysis was implemented in the rNeighborGWAS package34, which
internally uses the gaston package71 and proceeds as follows. The statistical significance, i.e., \(p\)-values of each parameter, was calculated based on a \({\chi }^{2}\) distribution with
one degree of freedom34. For \({\beta }_{2}\), a sample structure among individuals was corrected by a weighted kinship matrix \({{{\bf{K}}}}^{\prime}={\hat{\sigma
}}_{1}^{2}{{{{\bf{K}}}}}_{1}+{\hat{\sigma }}_{2}^{2}{{{{\bf{K}}}}}_{2}\)71. For the efficient testing of \({\beta }_{1}\) or \({\beta }_{2}\), we used the lmm.diago function of the gaston
package71 to apply eigenvalue decomposition for \({\hat{\sigma }}_{1}^{2}{{{{\bf{K}}}}}_{1}\) or \({{{\bf{K}}}}{\prime}\). The initial plant size, presence/absence of inflorescences, study
years, and differences in experimental blocks were considered non-genetic covariates. The genome-wide significance level for the \(p\)-values of \({\beta }_{1}\) or \({\beta }_{2}\) was
determined using the Bonferroni correction of multiple testing for all SNPs at \(p\) = 0.05. To empirically determine the significance threshold, we also performed a permutation test in
which neighboring plants within blocks or genomic positions were randomized (Supplementary Fig. 6 and Supplementary Note 1). We repeated the GWAS analysis at \(J\) = 0 (i.e., standard GWAS),
\(J\) = 4 (up to the nearest neighbors) and \(J\) = 12 (up to the second-nearest neighbors). If \({{{{\bf{K}}}}}_{2}\) is ignored, imperfect correction of the sample structure leads to
inflation or deflation of the \(p\)-values (Supplementary Fig. 16 and Supplementary Note 5). LIST OF CANDIDATE GENES Provided that linkage disequilibrium (LD) decays within 10 kbp on average
in the _A. thaliana_ genome72, we searched for candidate genes within 10 kbp near SNPs with the top 0.1% \(p\)-values. Functional annotation data from The Arabidopsis Information Resource
(TAIR) were used for the gene model and description of _A. thaliana_73. LASSO WITH FOCAL AND NEIGHBOR GENOTYPE EFFECTS MODIFIED NEIGHBOR GWAS FOR LASSO To perform multiple regressions on all
SNPs, we used sparse regression that could simultaneously select important SNP predictors and estimate their coefficients. The Neighbor GWAS model (Eq. 1) is expressed as a multiple
regression model as follows: $${{{\bf{y}}}}={{{{\bf{X}}}}}_{{{{\bf{0}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{0}}}}}+{{{{\bf{X}}}}}_{{{{\bf{1}}}}}{{{{\boldsymbol{\beta
}}}}}_{{{{\bf{1}}}}}+{{{{\bf{X}}}}}_{{{{\bf{2}}}}}{{{{\boldsymbol{\beta }}}}}_{{{{\bf{2}}}}}+{{{\bf{e}}}}$$ (3) where \(y\) is a phenotype vector; \({{{{\boldsymbol{\beta
}}}}}_{{{{\bf{0}}}}}\) is a vector including coefficients for an intercept and non-genetic covariates; \({{{{\boldsymbol{\beta }}}}}_{{{{\bf{1}}}}}\) and \({{{{\boldsymbol{\beta
}}}}}_{{{{\bf{2}}}}}\) are vectors including coefficients of focal and neighbor genotype effects, respectively; \({{{{\bf{X}}}}}_{0}\) is a matrix that includes a unit vector and non-genetic
covariates for \(n\) individuals. \({{{{\bf{X}}}}}_{1}\) is a matrix that includes the focal genotype values for \(n\) individuals and \(q\) SNP markers. \({{{{\bf{X}}}}}_{2}\) is a matrix
that includes the neighbor genotype similarity for \(n\) individuals and \(q\) SNP markers, as noted above (see the subsection ‘Neighbor GWAS model’ above). To simultaneously perform
variable selection and coefficient estimation, we applied the least absolute shrinkage and selection operator (LASSO)48 to Eq. 3. We further cut off 1,819,577 GWAS SNPs to 1,242,128 SNPs for
LASSO with the criterion of LD at \({r}^{2}\) < 0.8 between adjacent SNPs, because LASSO is sensitive to high correlations among explanatory variables. The initial plant size,
presence/absence of inflorescences, study years, and experimental blocks were considered fixed covariates. Important variables were selected from 1,242,128 SNP markers and the same number of
neighbor-related SNPs using LASSO. We used the Python (v3.6.8) version of the glmnet package v1.074 to perform the LASSO. The kinship and sample structure among individuals were implicitly
considered because LASSO regression can deal with all SNPs simultaneously. While a gradient of sparse regressions from the LASSO, via the elastic net, to the ridge regression was available
in the glmnet package74, we used the sparsest regression, LASSO, because of the computational burden of recursive calculation during the effect size estimation and simulation (see “The
effect size of mixed planting” below). To determine the LASSO regularization parameter \(\lambda\), we first trained the LASSO models with the learning data (2017 and 2018) and then
validated their outputs using the test dataset collected in another year (2019; see also “Field setting” above). The predictability of the four phenotypes was evaluated based on the
correlations between the predicted and observed values of each phenotype. Spearman’s rank correlation \(\rho\) was used because some phenotypic values were not normally distributed. The
predicted values were obtained from LASSO models with different values of \(\lambda\). To assess genetically based predictability, we quantified the observed phenotype values in 2019 as the
residuals of a standard linear model. This standard linear model incorporated the same non-genetic explanatory variables as the LASSO model, including the initial plant size, presence of
inflorescences, and difference in three experimental blocks, while each phenotype was considered a response variable. To determine whether the incorporation of neighbor genotypes improved
the correlation with the test data, we compared LASSO with or without neighbor genotypes across a series of \(\lambda\) values. If the neighbor-including LASSO yielded a larger correlation
than the neighbor-excluding LASSO at a given \(\lambda\), this indicates that neighbor genotypes were able to improve the predictability of a target phenotype by LASSO. In this context, the
maximum \(\rho\) of the neighbor-including LASSO was larger than that of the neighbor-excluding LASSO for herbivore damage in Zurich (Supplementary Fig. 10a). Furthermore, the
neighbor-including LASSO achieved this maximum \(\rho\) even with stringent regularization (= larger \(\lambda\)) compared to the neighbor-excluding LASSO (Supplementary Fig. 10a). For the
Otsu site, the neighbor-including LASSO also had slightly larger correlations with herbivore damage than the neighbor-excluding LASSO, supporting the improved predictability of herbivore
damage by neighbor genotypes at another site (Supplementary Fig. 10e). None of the community composition phenotypes, however, showed better predictability with neighbor-including LASSO
(Supplementary Fig. 10b–d, f–h). This was presumably because the individual number of the predominant species differed between study years (Supplementary Fig. 1b–g). These additional results
support the improved predictability of herbivore damage but suggest difficulty in predicting community composition by neighbor genotypes. When the neighbor-including LASSO outperformed the
neighbor-excluding ones at a given \(\lambda\), we obtained the vectors of the estimated coefficients \({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) that were able to improve the
phenotype prediction. LASSO could yield multiple sets of \({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) across a series of \(\lambda\) where the neighbor-including LASSO yielded larger
correlations. A larger \(\lambda\) tends to yield fewer non-zero SNPs with large coefficients, whereas a smaller \(\lambda\) tends to yield more non-zero SNPs with small coefficients. To
consider the polygenic basis of neighbor effects, we averaged the estimated coefficients \({\hat{\beta }}_{2}\) per SNP across the range of \(\lambda\), resulting in 756 SNPs with non-zero
\({\beta }_{2}\) for herbivore damage in Zurich (see “Results” in the main text). This estimated vector of neighbor coefficients \({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) was used
to estimate the effect size. POST-LASSO ANALYSIS (I): THE EFFECT SIZE OF MIXED PLANTING To estimate the pairwise effect size of mixed planting, we extrapolated the LASSO model (Eq. 3) under
a virtual monoculture (a pair of the same accessions) or pairwise mixture (a pair of different accessions). The pairwise effect size was determined by the difference in the linear sum
\([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\cdot {\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}-[{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{i}]\cdot
{\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) between a pair of accessions. The first term \([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\cdot {\hat{{{{\boldsymbol{\beta
}}}}}}_{{{{\bf{2}}}}}\) represents the phenotype values expected from different genotype vectors between accessions \(i\) and \(j\) (= pairwise mixture), whereas the second term
\([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{i}]\cdot {\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) represents those expected from the same genotype vectors between accessions
\(i\) and \(i\) (= monoculture). The element-wise product \([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\) or \([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{i}]\) represents the
neighbor genotype similarity between a pair of different or the same accessions, respectively. The neighbor genotype effects turned out to have no significant SNPs (Figs. 2e–h, m–p, 3a–d,
and i–l); therefore, the genotype pairs predicted by many moderate-effect loci were suitable for testing the estimated effects of mixed planting. In contrast, genotype pairs showing the
largest effect size were selected based on a few large-effect but less reliable loci. Assuming that multiple moderate-effect loci could result in the effects of mixed planting, we avoided
the extreme tail of the effect size distribution when focusing on the three pairs: a pair with a large positive effect, Bg-2 and Uod-1 (effect size = 0.8); a pair with a moderate positive
effect, Vastervik and Jm-0 (0.23); a pair with a slight positive effect, Bro1-6 and Bla-1 (0.1) (Fig. 4a). Note also that \({\beta }_{2}\) in the neighbor GWAS models (Eqs. 1 and 3) denotes
symmetric interactions between the focal \(i\) and neighbor \(j\) individuals34, and thus \([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\) and \([{{{{\bf{x}}}}}_{j}\; \circ \;\;
{{{{\bf{x}}}}}_{i}]\) exert the same effects on a target phenotype. To test whether the increasing number of plant genotypes increases or decreases herbivore damage, we also simulated
herbivore damage in Zurich, i.e., ln(no. of leaf holes+1) using the estimated vector of neighbor coefficients \({\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\). Assuming the nearest
neighbors in a two-dimensional lattice, we simulated mixtures of up to eight genotypes. The herbivore damage was predicated by its marginal value with respect to the net neighbor effects
\([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\cdot {\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\). To examine the overall and selected patterns, we tested two types of genotype
selection: (i) random selection from all pairs or (ii) random selection from pairs with positive estimates of pairwise mixed planting (positive values in Fig. 4a). First, eight genotypes
were randomly selected from the 199 accessions to represent the overall pattern (Fig. 4c). We listed one (monoculture), two, four, or eight (full mixture) genotype combinations among the
selected eight genotypes and averaged their predicted damage \([{{{{\bf{x}}}}}_{i}\; \circ \;\; {{{{\bf{x}}}}}_{j}]\cdot {\hat{{{{\boldsymbol{\beta }}}}}}_{{{{\bf{2}}}}}\) among all the
combinations. Second, four positively interacting pairs (_x_-axis > 0 in Fig. 4a) were randomly selected to test whether the random selection of positive pairwise interactions yielded
positive relationships between genotype number and anti-herbivore resistance (Supplementary Fig. 11f). Duplicates of accessions were not allowed when selecting four pairs of two paired
accessions. This line of random sampling was performed 9999 times to calculate the mean and standard deviation. In the first case, Fig. 4c shows the negative relationship between the number
of genotypes and plant resistance. In the second case, herbivore damage decreased by paired mixing but increased by four- and eight-genotype mixing (Supplementary Fig. 11f). This was because
scaling up pairwise mixtures to four or eight genotypes confounded negatively interacting pairs. In addition to Fig. 4a, c, these supplementary results also support the difficulty in
targeting the positive relationships between genotype richness and anti-herbivore resistance. POST-LASSO ANALYSIS (II): GO ENRICHMENT ANALYSIS To infer the category of genes related to
positive and negative neighbor effects, we performed gene ontology (GO) enrichment analyses for candidate genes near LASSO-selected SNPs (i.e., SNPs with non-zero \({\hat{\beta }}_{2}\)).
Same as the list of candidate genes in GWAS, we searched for genes within 10 kbp around each selected SNP. We omitted duplicated genes after listing the candidate genes. We then performed
Fisher’s exact probability tests for each GO category against the entire gene set of _A. thaliana_. Multiple testing for genes was corrected using a false discovery rate (FDR)75. The entire
set was built upon TAIR GO slim annotation73 using the GO.db package v3.17.076 in R. To summarize the results of the GO enrichment analysis, we applied the REVIGO algorithm77 to the list of
significant GO terms at FDR \( < 0.05\). When summarizing the significant GO terms, we focused on the Biological Process with the similarity measure at 0.7 (i.e., the same as the default
setting). The rrvgo v1.12.078 and org.At.tair.db v3.17.079 packages in R were used to run the REVIGO algorithm. This line of GO analysis was separately performed for SNPs with negative or
positive \({\hat{\beta }}_{2}\) to detect GO terms unique to positive or negative neighbor effects on anti-herbivore resistance. Note also that post-GWAS GO analyses possess the issue of
statistical non-independence due to LD in the standard GWAS80. However, LASSO was less likely to be subject to this issue because (i) this sparse regression could sparsely select SNP
variables across a genome, (ii) we pruned adjacent SNPs on the strong LD at \({r}^{2}\) > 0.8, and (iii) we focused on unique genes before using Fisher’s test. Therefore, we applied the
conventional GO enrichment test based on Fisher’s test with FDR correction to the LASSO results. The in-house R package that includes utility functions of the GO enrichment analysis is
available at Zenodo81. MIXED PLANTING EXPERIMENT FIELD EXPERIMENT To test the effects of mixed planting on herbivore damage, we transplanted three pairs of accessions (i.e., Bg-2 and Uod-1;
Vastervik and Jm-0; and Bla-1 and Bro1-6) under mixture and monoculture conditions. The theory of plant neighbor effects suggests that both the plant patch size and neighbor composition
should be manipulated to distinguish the effects of mixed planting from the density-dependent attraction of herbivores16,82. Therefore, we set large and small plant patches in addition to
monoculture or mixture conditions. The field experiment was conducted from late June to July 2019 and 2021 in the outdoor garden of the University of Zurich-Irchel. Plants were first grown
under short-day conditions and then transferred to the outdoor garden following the same procedure as the field experiment for GWAS above. Two accessions were then mixed in a checkered
manner under the mixture condition, whereas either of the two accessions was placed under the monoculture condition. The large patch included 64 potted plants in 8 \(\times\) 8 trays and had
a single replicate, whereas the small patch included 16 plants in 4 \(\times\) 4 trays and had three replicates (upper photographs in Supplementary Fig. 12). In the mixture setting, the two
potted accessions filled the square space in a checkered manner without a blank position (upper photographs in Supplementary Fig. 12). The total number of initial plants was two accessions
\(\times\) three pairs \(\times\) mixture or monoculture \(\times\) large or small patches \(\times\) two years = 2016 individuals. Only a few pots per plot were labeled to track the plots
in the field, whereas the other pots were not labeled to blind their information. The initial plant size was measured in the same manner as in the field GWAS. Leaf holes were counted three
weeks after transplantation. Four plants died during the field experiment, resulting in a final sample size of 2012 plants. STATISTICAL ANALYSIS We analyzed the herbivore damage (i.e., the
number of leaf holes per plant) as a response variable. Linear mixed models were used for the number of leaf holes because this variable appeared to be normally distributed. The number of
leaf holes was ln(x + 1)-transformed to improve the normality. The explanatory variables were plant accession, mixture or monoculture conditions, small or large patches, and study years. The
initial plant size, represented by the length of the largest leaf (mm), was considered as an offset term. Two-way interactions were also considered among the plant accessions, mixture
conditions, and patch conditions. Because the large and small patches had different numbers of individual plants, this imbalance was dealt with using a random factor. We split the large
patch by 4 \(\times\) 4 potted plants (= the same size as the small patch; see also photographs in Supplementary Fig. 12), and considered these subplot differences — i.e., the total of 126
subplots — as a random effect. The significance of each explanatory variable was tested using Type III analysis of variance based on Satterthwaite’s effective degrees of freedom and
\(F\)-tests83. To compare herbivore damage for each accession between the mixture and monoculture conditions, we calculated marginal means for the full model based on Satterthwaite’s method
with Sidak correction of multiple testing for accessions84. For the analyses of leaf holes, we used the lme4 v1.1-3485, lmerTest v3.1-383, and emmeans v1.8.784 packages in R. Box plots
visualize the median with upper and lower quartile, with whiskers extending to 1.5 \(\times\) inter-quartile range. To examine the effects of patch size and year in addition to mixed
planting (Fig. 4d), we analyzed a separate dataset for patch conditions and study years (Supplementary Fig. 12a–d and Supplementary Table 5). Consistent with the order of the estimated
effect size (Fig. 4a), the marginal means across these conditions showed the largest sum of the effects of mixed planting between Bg-2 and Uod-1 (= 0.495 in Supplementary Table 4b) and the
second largest effect between Vastervik and Jm-0 (= 0.453 in Supplementary Table 4b). The significant effects of mixed planting on herbivore damage were more detectable in the large patches
than in the small patches (Supplementary Fig. 12). The Bg-2 and Uod-1 accessions showed a significant reduction in herbivore damage among five cases out of the two accessions \(\times\) two
years \(\times\) two patch conditions (Supplementary Fig. 12 and Supplementary Table 5) and a marginally significant case in the small patch (\(p\) = 0.053 in Supplementary Table 5a). The
Vastervik and Jm-0 showed three significantly positive cases favoring the reduction in herbivore damage out of the eight conditions (Supplementary Fig. 12 and Supplementary Table 5),
indicating less consistency than the Bg-2 and Uod-1 pairs under diverse conditions. The Bla-1 and Bro1-6 pairs did not have significantly positive cases favoring the reduction in herbivore
damage out of the eight conditions and even had one case of increased damage by mixed planting (Supplementary Fig. 12 and Supplementary Table 5). The main results and separate data show that
the order of the observed mixing effects is consistent with that of the estimated effect size. LABORATORY CHOICE EXPERIMENT INSECT MATERIALS To examine the feeding by flea beetles, we
conducted laboratory choice experiments using one of the two major flea beetles, the black flea beetle _Phyllotreta astrachanica_. Adult _P. astrachanica_ were collected from _Brassica_ spp.
at the University of Zurich-Irchel. Adults and larvae were reared on German turnips (Kohlrabi) following a previously established protocol86. The species of flea beetles were identified
based on the DNA sequence of the mitochondrial gene encoding cytochrome c oxidase subunit I (_COI_). DNA was extracted using ZYMO RESEARCH Quick-DNA Tissue/Insect Kits (cat. no. D6016). We
used universal COI primers designed by Folmer et al.87 for Polymerase Chain Reaction (PCR) amplification under the following conditions: Initial denaturation at 95 °C for 5 minutes followed
by 40 cycles of 95 °C for 15 s, 50 °C for 30 s, 72 °C for 60 s and a final extension at 72 °C for 3 min. The PCR products were sequenced using Sanger sequencing. We compared our sequences
with the COI sequences registered by Hendrich et al.88, which included 15 _Phyllotreta_ species with several individual vouchers per species collected in Central Europe. Our sequences and
the registered sequences were clustered using a neighbor-joining tree and the default alignment method implemented in the Qiagen CLC Main Workbench. We identified the species from our
samples based on phylogenetic clusters. Our sequence data were registered in GenBank with IDs OQ857829 to OQ857834, which included three individuals of black- and yellow-striped flea
beetles. EXPERIMENTAL SETTING We used the three pairs of six _A. thaliana_ accessions, Bg-2 vs. Uod-1, Vastervik vs. Jm-0, and Bla-1 vs. Bro1-6. Seeds were sown on Jiffy-seven pots (33-mm
diameter) and stratified at 4 °C for a week. Seedlings were cultivated under long-day conditions (16 h light: 8 h dark, 22/20 °C) for 3 weeks, with liquid fertilizer added a week after the
start of cultivation. Two adult beetles were allowed to feed on the mixture of two individuals \(\times\) two accessions for three days under long-day conditions (Supplementary Fig. 13a).
The feeding arena was constructed using a transparent plastic cup (129 mm in diameter and 60 mm in height) that enclosed four Jiffy-potted seedlings. Excluding cups without any infestation
by _P. astrachanica_, we obtained 15–20 replicates of feeding arena per pair. STATISTICAL ANALYSIS We analyzed the herbivore damage (i.e., the number of leaf holes per plant) as a response
variable using generalized linear models. Negative binomial errors and a log-link function were chosen because the number of leaf holes was zero-truncated (Supplementary Fig. 13b). Plant
accessions and arena IDs were included as the explanatory variables. Likelihood ratio tests based on a \({\chi }^{2}\)-distribution were used after checking whether the ratio of residual
deviance to the residual degree of freedom was nearly one. The significance of each explanatory variable was tested by excluding one variable from the full model. The glm.nb function in the
MASS package in R was used for generalized linear models with negative binomial errors. Likelihood ratio tests showed that flea beetles showed a significant preference between Bg-2 and Uod-1
and between Vastervik and Jm-0 but not between Bla-1 and Bro1-6 (Supplementary Table 6). The effect of the experimental area on leaf holes explained deviance but was only significant in the
Bg-2 and Uod-1 pairs (Supplementary Table 6). REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article. DATA
AVAILABILITY Phenotype data obtained in this study are available in the GitHub repository (https://github.com/yassato/AraHerbNeighborGen) and in Zenodo
(https://doi.org/10.5281/zenodo.7945317)64. Mitochondrial COI sequences obtained from flea beetles are registered in GenBank with the accession numbers
OQ857829OQ857830OQ857831OQ857832OQ857833OQ857834. Plant genotype data are available at the AraGWAS Catalog website (https://aragwas.1001genomes.org/#/download-center)63. Source data are
provided in this paper. CODE AVAILABILITY All the source codes are available in the GitHub repository (https://github.com/yassato/AraHerbNeighborGen) and in Zenodo
(https://doi.org/10.5281/zenodo.7945317)64. REFERENCES * Laikre, L. et al. Post-2020 goals overlook genetic diversity. _Science_ 367, 1083–1085 (2020). Article ADS PubMed Google Scholar
* Exposito-Alonso, M. et al. Genetic diversity loss in the Anthropocene. _Science_ 377, 1431–1435 (2022). Article ADS CAS PubMed Google Scholar * Barbour, M. A., Kliebenstein, D. J.
& Bascompte, J. A keystone gene underlies the persistence of an experimental food web. _Science_ 376, 70–73 (2022). Article ADS CAS PubMed Google Scholar * Stange, M., Barrett, R.
D. & Hendry, A. P. The importance of genomic variation for biodiversity, ecosystems and people. _Nat. Rev. Genet._ 22, 89–105 (2021). Article CAS PubMed Google Scholar * Schmid, B.
Effects of genetic diversity in experimental stands of _Solidago altissima_–evidence for the potential role of pathogens as selective agents in plant populations. _J. Ecol_ 82, 165–175
(1994). * Crutsinger, G. M. et al. Plant genotypic diversity predicts community structure and governs an ecosystem process. _Science_ 313, 966–968 (2006). Article ADS CAS PubMed Google
Scholar * Hughes, A. R., Inouye, B. D., Johnson, M. T., Underwood, N. & Vellend, M. Ecological consequences of genetic diversity. _Ecol. Lett._ 11, 609–623 (2008). Article PubMed
Google Scholar * Utsumi, S., Ando, Y., Craig, T. P. & Ohgushi, T. Plant genotypic diversity increases population size of a herbivorous insect. _Proc. R. Soc. B Biol. Sci._ 278,
3108–3115 (2011). Article Google Scholar * Koricheva, J. & Hayes, D. The relative importance of plant intraspecific diversity in structuring arthropod communities: A meta-analysis.
_Funct. Ecol._ 32, 1704–1717 (2018). Article Google Scholar * Raffard, A., Santoul, F., Cucherousset, J. & Blanchet, S. The community and ecosystem consequences of intraspecific
diversity: A meta-analysis. _Biol. Rev._ 94, 648–661 (2019). Article PubMed Google Scholar * Barbosa, P. et al. Associational resistance and associational susceptibility: Having right or
wrong neighbors. _Annu. Rev. Ecol. Evol. Syst._ 40, 1–20 (2009). Article Google Scholar * Sato, Y. Associational effects and the maintenance of polymorphism in plant defense against
herbivores: Review and evidence. _Plant Species Biol._ 33, 91–108 (2018). Article Google Scholar * Jactel, H., Moreira, X. & Castagneyrol, B. Tree diversity and forest resistance to
insect pests: Patterns, mechanisms, and prospects. _Annu. Rev. Entomol._ 66, 277–296 (2021). Article CAS PubMed Google Scholar * Tahvanainen, J. O. & Root, R. B. The influence of
vegetational diversity on the population ecology of a specialized herbivore, _Phyllotreta cruciferae_ (Coleoptera: Chrysomelidae). _Oecologia_ 10, 321–346 (1972). Article ADS PubMed
Google Scholar * White, J. A. & Whitham, T. G. Associational susceptibility of cottonwood to a box elder herbivore. _Ecology_ 81, 1795–1803 (2000). Article Google Scholar * Hambäck,
P. A., Inouye, B. D., Andersson, P. & Underwood, N. Effects of plant neighborhoods on plant–herbivore interactions: Resource dilution and associational effects. _Ecology_ 95, 1370–1383
(2014). Article PubMed Google Scholar * Pickett, J. A., Woodcock, C. M., Midega, C. A. & Khan, Z. R. Push–pull farming systems. _Curr. Opin. Biotechnol._ 26, 125–132 (2014). Article
CAS PubMed Google Scholar * Hambäck, P. A., Agren, J. & Ericson, L. Associational resistance: Insect damage to purple loosestrife reduced in thickets of sweet gale. _Ecology_ 81,
1784–1794 (2000). Article Google Scholar * Jactel, H., Birgersson, G., Andersson, S. & Schlyter, F. Non-host volatiles mediate associational resistance to the pine processionary moth.
_Oecologia_ 166, 703–711 (2011). Article ADS CAS PubMed Google Scholar * Sato, Y. & Kudoh, H. Herbivore-mediated interaction promotes the maintenance of trichome dimorphism through
negative frequency-dependent selection. _Am. Nat._ 190, E67–E77 (2017). Article PubMed Google Scholar * Bustos-Segura, C., Poelman, E. H., Reichelt, M., Gershenzon, J. & Gols, R.
Intraspecific chemical diversity among neighbouring plants correlates positively with plant size and herbivore load but negatively with herbivore damage. _Ecol. Lett._ 20, 87–97 (2017).
Article PubMed Google Scholar * Karban, R. & Maron, J. The fitness consequences of interspecific eavesdropping between plants. _Ecology_ 83, 1209–1213 (2002). Article Google Scholar
* Barton, K. E. & Bowers, M. D. Neighbor species differentially alter resistance phenotypes in _Plantago_. _Oecologia_ 150, 442–452 (2006). Article ADS PubMed Google Scholar *
Letourneau, D. K. The enemies hypothesis: Tritrophic interactions and vegetational diversity in tropical agroecosystems. _Ecology_ 68, 1616–1622 (1987). Article PubMed Google Scholar *
Aartsma, Y. et al. Spatial scale, neighbouring plants and variation in plant volatiles interactively determine the strength of host–parasitoid relationships. _Oikos_ 129, 1429–1439 (2020).
Article ADS Google Scholar * Tooker, J. F. & Frank, S. D. Genotypically diverse cultivar mixtures for insect pest management and increased crop yields. _J. Appl. Ecol._ 49, 974–985
(2012). Article Google Scholar * Whitham, T. G. et al. Extending genomics to natural communities and ecosystems. _Science_ 320, 492–495 (2008). Article ADS CAS PubMed Google Scholar *
Turner, K. G., Lorts, C. M., Haile, A. T. & Lasky, J. R. Effects of genomic and functional diversity on stand-level productivity and performance of non-native _Arabidopsis_. _Proc. R.
Soc. B Biol. Sci._ 287, 20202041 (2020). Article Google Scholar * Wuest, S. E. et al. Increasing plant group productivity through latent genetic variation for cooperation. _PLoS Biol._ 20,
e3001842 (2022). Article CAS PubMed PubMed Central Google Scholar * Montazeaud, G., Helleu, Q., Wuest, S. E. & Keller, L. Indirect genetic effects are shaped by demographic history
and ecology in _Arabidopsis thaliana_. _Nat. Ecol. Evol._ 7, 1878–1891 (2023). Article PubMed Google Scholar * Wuest, S. E. et al. Single-gene resolution of diversity-driven overyielding
in plant genotype mixtures. _Nat. Commun._ 14, 3379 (2023). Article ADS CAS PubMed PubMed Central Google Scholar * Horton, M. W. et al. Genome-wide patterns of genetic variation in
worldwide _Arabidopsis thaliana_ accessions from the RegMap panel. _Nat. Genet._ 44, 212–216 (2012). Article CAS PubMed PubMed Central Google Scholar * Alonso-Blanco, C. et al. 1,135
genomes reveal the global pattern of polymorphism in _Arabidopsis thaliana_. _Cell_ 166, 481–491 (2016). Article Google Scholar * Sato, Y., Yamamoto, E., Shimizu, K. K. & Nagano, A. J.
Neighbor GWAS: Incorporating neighbor genotypic identity into genome-wide association studies of field herbivory. _Heredity_ 126, 597–614 (2021). Article CAS PubMed PubMed Central
Google Scholar * Ising, E. Beitrag zur theorie des ferromagnetismus. _Z. Phys. A Hadron. Nucl._ 31, 253–258 (1925). CAS Google Scholar * Weber, M. & Buceta, J. The cellular Ising
model: A framework for phase transitions in multicellular environments. _J. R. Soc. Interface_ 13, 20151092 (2016). Article PubMed PubMed Central Google Scholar * Jahanbakhsh, E. &
Milinkovitch, M. C. Modeling convergent scale-by-scale skin color patterning in multiple species of lizards. _Curr. Biol._ 32, 5069–5082.e13 (2022). Article CAS PubMed PubMed Central
Google Scholar * Schlicht, R. & Iwasa, Y. Forest gap dynamics and the Ising model. _J. Theor. Biol._ 230, 65–75 (2004). Article ADS MathSciNet PubMed Google Scholar * Züst, T.
& Agrawal, A. A. Mechanisms and evolution of plant resistance to aphids. _Nat. Plants_ 2, 15206 (2016). Article PubMed Google Scholar * Mertens, D. et al. Plant defence to sequential
attack is adapted to prevalent herbivores. _Nat. Plants_ 7, 1347–1353 (2021). Article PubMed Google Scholar * Yang, J., Wei, J. & Kang, L. Feeding of pea leafminer larvae
simultaneously activates jasmonic and salicylic acid pathways in plants to release a terpenoid for indirect defense. _Insect Sci._ 28, 811–824 (2021). Article CAS PubMed Google Scholar *
Sato, Y., Shimizu-Inatsugi, R., Yamazaki, M., Shimizu, K. K. & Nagano, A. J. Plant trichomes and a single gene _GLABRA1_ contribute to insect community composition on field-grown
_Arabidopsis thaliana_. _BMC Plant Biol._ 19, 163 (2019). Article PubMed PubMed Central Google Scholar * Brachi, B. et al. Coselected genes determine adaptive variation in herbivore
resistance throughout the native range of _Arabidopsis thaliana_. _Proc. Natl. Acad. Sci. USA_ 112, 4032–4037 (2015). Article ADS CAS PubMed PubMed Central Google Scholar * Nordborg,
M. et al. The pattern of polymorphism in _Arabidopsis thaliana_. _PLoS Biol._ 3, e196 (2005). Article PubMed PubMed Central Google Scholar * Sasaki, E., Gunis, J., Reichardt-Gomez, I.,
Nizhynska, V. & Nordborg, M. Conditional GWAS of non-CG transposon methylation in _Arabidopsis thaliana_ reveals major polymorphisms in five genes. _PLoS Genet._ 18, e1010345 (2022).
Article CAS PubMed PubMed Central Google Scholar * Sato, Y., Takahashi, Y., Xu, C. & Shimizu, K. K. Detecting frequency-dependent selection through the effects of genotype
similarity on fitness components. _Evolution_ 77, 1145–1157 (2023). Article PubMed Google Scholar * Gondro, C., Van Der Werf, J. H. & Hayes, B. _Genome-Wde Association Studies and
Genomic Prediction_. (Humana Press, NY, USA, 2013). * Tibshirani, R. Regression shrinkage and selection via the lasso. _J. R. Stat. Soc. Ser. B Methodol._ 58, 267–288 (1996). Article
MathSciNet Google Scholar * Mochizuki, S., Sugimoto, K., Koeduka, T. & Matsui, K. Arabidopsis lipoxygenase 2 is essential for formation of green leaf volatiles and five-carbon
volatiles. _FEBS Lett._ 590, 1017–1027 (2016). Article CAS PubMed Google Scholar * Schuman, M. C., Allmann, S. & Baldwin, I. T. Plant defense phenotypes determine the consequences of
volatile emission for individuals and neighbors. _eLife_ 4, e04490 (2015). Article PubMed PubMed Central Google Scholar * Meuwissen, T. H. E., Hayes, B. J. & Goddard, M. E.
Prediction of total genetic value using genome-wide dense marker maps. _Genetics_ 157, 1819–1829 (2001). Article CAS PubMed PubMed Central Google Scholar * De Los Campos, G. et al.
Predicting quantitative traits with regression models for dense molecular markers and pedigree. _Genetics_ 182, 375–385 (2009). Article Google Scholar * Crossa, J. et al. Genomic selection
in plant breeding: Methods, models, and perspectives. _Trends Plant Sci._ 22, 961–975 (2017). Article CAS PubMed Google Scholar * Lorenzo, C. D. et al. BREEDIT: A multiplex genome
editing strategy to improve complex quantitative traits in maize. _Plant Cell_ 35, 218–238 (2023). Article PubMed Google Scholar * Shimizu, K. K., Kudoh, H. & Kobayashi, M. J. Plant
sexual reproduction during climate change: Gene function in natura studied by ecological and evolutionary systems biology. _Ann. Bot._ 108, 777–787 (2011). Article CAS PubMed PubMed
Central Google Scholar * Sato, Y. et al. Transcriptional variation in glucosinolate biosynthetic genes and inducible responses to aphid herbivory on field-grown _Arabidopsis thaliana_.
_Front. Genet._ 10, 787 (2019). Article CAS PubMed PubMed Central Google Scholar * Zaidem, M. L., Groen, S. C. & Purugganan, M. D. Evolutionary and ecological functional genomics,
from lab to the wild. _Plant J._ 97, 40–55 (2019). Article CAS PubMed Google Scholar * Stockenhuber, R. et al. UV RESISTANCE LOCUS 8–mediated UV-B response is required alongside
CRYPTOCHROME 1 for plant survival in sunlight under field conditions. _Plant Cell Physiol._ 65, 35–48 (2024). Article PubMed Google Scholar * Zeller, S. L., Kalinina, O., Flynn, D. F.
& Schmid, B. Mixtures of genetically modified wheat lines outperform monocultures. _Ecol. Appl._ 22, 1817–1826 (2012). Article PubMed Google Scholar * Atwell, S. et al. Genome-wide
association study of 107 phenotypes in _Arabidopsis thaliana_ inbred lines. _Nature_ 465, 627–631 (2010). Article ADS CAS PubMed PubMed Central Google Scholar * Horton, M. W. et al.
Genome-wide association study of _Arabidopsis thaliana_ leaf microbial community. _Nat. Commun._ 5, 5320 (2014). Article ADS PubMed Google Scholar * Chan, E. K., Rowe, H. C. &
Kliebenstein, D. J. Understanding the evolution of defense metabolites in _Arabidopsis thaliana_ using genome-wide association mapping. _Genetics_ 185, 991–1007 (2010). Article CAS PubMed
PubMed Central Google Scholar * Togninalli, M. et al. AraPheno and the AraGWAS catalog 2020: A major database update including RNA-seq and knockout mutation data for _Arabidopsis
thaliana_. _Nucleic Acids Res._ 48, D1063–D1068 (2020). CAS PubMed Google Scholar * Sato, Y. et al. AraHerbNeighborGen: Arabidopsis herbivory data with the analysis of neighbor genotypic
effects (v1.1.2). _Zenodo_ https://doi.org/10.5281/zenodo.7945317 (2024). * Takimoto, H., Sato, Y., Nagano, A. J., Shimizu, K. K. & Kanagawa, A. Using a two-stage convolutional neural
network to rapidly identify tiny herbivorous beetles in the field. _Ecol. Inform._ 66, 101466 (2021). Article Google Scholar * Tooker, J. F. & Giron, D. The evolution of endophagy in
herbivorous insects. _Front. Plant Sci._ 11, 581816 (2020). Article PubMed PubMed Central Google Scholar * Oksanen, J. et al. _Vegan: Community Ecology Package_.
https://CRAN.R-project.org/package=vegan (2020). * R. Core Team. _R: A Language and Environment for Statistical Computing_. R Foundation for Statistical Computing, Vienna, Austria (2019). *
Seren, Ü. et al. GWAPP: A web application for genome-wide association mapping in _Arabidopsis_. _Plant Cell_ 24, 4793–4805 (2013). Article Google Scholar * Schneider, K. A. Maximization
principles for frequency-dependent selection I: The one-locus two-allele case. _Theor. Popul. Biol._ 74, 251–262 (2008). Article PubMed Google Scholar * Perdry, H. & Dandine-Roulland,
C. _Gaston: Genetic Data Handling (QC, GRM, LD, PCA) & Linear Mixed Models_. https://CRAN.R-project.org/package=gaston (2020). * Kim, S. et al. Recombination and linkage disequilibrium
in _Arabidopsis thaliana_. _Nat. Genet._ 39, 1151–1155 (2007). Article CAS PubMed Google Scholar * Berardini, T., Reiser, L. & Huala, E. _TAIR functional annotation data_.
https://doi.org/10.5281/zenodo.7159104 (2021). * Balakumar, B. J., Hastie, T., Friedman, J., Tibshirani, R. & Simon, N. _glmnet for Python_. (2016).
http://hastie.su.domains/glmnet_python/ (accessed 19 September 2019). * Benjamini, Y. & Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple
testing. _J. R. Stat. Soc. Ser. B Methodol._ 57, 289–300 (1995). Article MathSciNet Google Scholar * Carlson, M. _GO.db: A set of annotation maps describing the entire Gene Ontology_.
https://doi.org/10.18129/B9.bioc.GO.db (2020). * Supek, F., Bošnjak, M., Škunca, N. & Šmuc, T. REVIGO summarizes and visualizes long lists of gene ontology terms. _PLoS ONE_ 6, e21800
(2011). Article ADS CAS PubMed PubMed Central Google Scholar * Sayols, S. _rrvgo: A bioconductor package to reduce and visualize gene ontology terms_.
https://doi.org/10.18129/B9.bioc.rrvgo (2020). * Carlson, M. _org.At.tair.db: Genome wide annotation for Arabidopsis_. https://doi.org/10.18129/B9.bioc.org.At.tair.db (2019). * Kofler, R.
& Schlötterer, C. Gowinda: Unbiased analysis of gene set enrichment for genome-wide association studies. _Bioinformatics_ 28, 2084–2085 (2012). Article CAS PubMed PubMed Central
Google Scholar * Sato, Y. & Nagano, A. J. GOfisher. _Zenodo_ https://doi.org/10.5281/zenodo.7901509 (2023). * Underwood, N., Inouye, B. D. & Hambäck, P. A. A conceptual framework
for associational effects: When do neighbors matter and how would we know? _Q. Rev. Biol._ 89, 1–19 (2014). Article PubMed Google Scholar * Kuznetsova, A., Brockhoff, P. B. &
Christensen, R. H. B. lmerTest package: Tests in linear mixed effects models. _J. Stat. Softw._ 82, 1–26 (2017). Article Google Scholar * Lenth, R. V. _Emmeans: Estimated marginal means,
aka least-squares means_ https://CRAN.R-project.org/package=emmeans (2021). * Bates, D., Mächler, M., Bolker, B. & Walker, S. Fitting linear mixed-effects models using lme4. _J. Stat.
Softw._ 67, 1–48 (2015). Article Google Scholar * Sato, Y., Takeda, K. & Nagano, A. J. Neighbor QTL: An interval mapping method for quantitative trait loci underlying plant
neighborhood effects. _G3:Genes|Genomes|Genet._ 11, jkab017 (2021). Article CAS PubMed PubMed Central Google Scholar * Folmer, O., Black, M., Hoeh, W., Lutz, R. & Vrijenhoek, R. DNA
primers for amplification of mitochondrial cytochrome c oxidase subunit I from diverse metazoan invertebrates. _Mol. Mar. Biol. Biotechnol._ 3, 294–299 (1994). CAS PubMed Google Scholar
* Hendrich, L. et al. A comprehensive barcode database for Central European beetles with a focus on Germany: Adding more than 3500 identified species to BOLD. _Mol. Ecol. Resour._ 15,
795–818 (2015). Article CAS PubMed Google Scholar Download references ACKNOWLEDGEMENTS The authors thank K.K. Thomsen, L. Mohn, M. Brasser, and all members of the Shimizu group for help
with the field setup in Zurich; G. Yumoto, L.G. Kawaguchi for field assistance in Otsu; T. Tsuchimatsu and S. Utsumi for discussions during the study; M. Yamazaki for advice on the
_Arabidopsis_ cultivation and molecular experiments; F. Beran for advice on the DNA barcoding of flea beetles; and J. Bascompte, M.A. Barbour, and S.E. Wuest for comments on the manuscript.
This study was supported by the Japan Science and Technology Agency (Grant numbers, JPMJPR17Q4 to Y.S., JPMJCR16O3 to K.K.S., JPMJCR15O2 and JPMJFR210B to A.J.N.); Japan Society for the
Promotion of Science (JP22H02316 to K.K.S. JP16J30005, JP20K15880, and JP23K14270 to Y.S., JP20H00423, and JP23H00386 to A.J.N.); Japanese Ministry of Education, Culture, Sports, Science and
Technology (JP22H05179 to K.K.S., and JP23H04967 to A.J.N.); Swiss National Science Foundation (CRSK-3_221418 to Y.S., 310030_212674 to R.S.I., 31003A_182318 and 310030_212551 to K.K.S.);
University Research Priority Program “Global Change and Biodiversity” from the University of Zurich to B.S. and K.K.S.; and the joint usage program of the Center for Ecological Research of
Kyoto University. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Evolutionary Biology and Environmental Studies, University of Zurich, Winterthurerstrasse 190, CH-8057, Zurich,
Switzerland Yasuhiro Sato, Rie Shimizu-Inatsugi & Kentaro K. Shimizu * Research Institute for Food and Agriculture, Ryukoku University, Yokotani 1-5, Seta Oe-cho, 520-2194, Otsu, Shiga,
Japan Yasuhiro Sato & Kazuya Takeda * Faculty of Environmental Earth Science, Hokkaido University, N10W5 Kita-ku, 060-0810, Sapporo, Hokkaido, Japan Yasuhiro Sato * Department of
Geography, University of Zurich, Winterthurerstrasse 190, CH-8057, Zurich, Switzerland Bernhard Schmid * Faculty of Agriculture, Ryukoku University, Yokotani 1-5, Seta Oe-cho, 520-2194,
Otsu, Shiga, Japan Atsushi J. Nagano * Institute for Advanced Biosciences, Keio University, 403-1 Nipponkoku, Daihouji, 997-0017, Tsuruoka, Yamagata, Japan Atsushi J. Nagano * Kihara
Institute for Biological Research, Yokohama City University, Maioka 641-12, Totsuka-ward, 244-0813, Yokohama, Japan Kentaro K. Shimizu Authors * Yasuhiro Sato View author publications You
can also search for this author inPubMed Google Scholar * Rie Shimizu-Inatsugi View author publications You can also search for this author inPubMed Google Scholar * Kazuya Takeda View
author publications You can also search for this author inPubMed Google Scholar * Bernhard Schmid View author publications You can also search for this author inPubMed Google Scholar *
Atsushi J. Nagano View author publications You can also search for this author inPubMed Google Scholar * Kentaro K. Shimizu View author publications You can also search for this author
inPubMed Google Scholar CONTRIBUTIONS Y.S., A.J.N., and K.K.S. conceived this study. Y.S. and R.S.-I. designed the field experiments and collected the data. K.T. and Y.S. designed the
laboratory choice experiments and collected the data. Y.S. designed the model and analyzed the data with statistical inputs from B.S. Y.S., and K.K.S. wrote a draft and revised the
manuscript with substantial inputs from R.S.-I., B.S., and A.J.N. All the authors contributed to the discussion and improvement of the manuscript. CORRESPONDING AUTHORS Correspondence to
Yasuhiro Sato, Atsushi J. Nagano or Kentaro K. Shimizu. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature
Communications_ thanks Arthur Korte and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION
PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION
41467_2024_52374_MOESM1_ESM.PDF Supplementary Information for “Reducing herbivory in mixed planting by genomic prediction of neighbor effects in the field” PEER REVIEW FILE DESCRIPTION OF
ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY DATASET 1 SUPPLEMENTARY DATASET 2 SUPPLEMENTARY DATASET 3 SUPPLEMENTARY DATASET 4 REPORTING SUMMARY SOURCE DATA SOURCE DATA RIGHTS AND
PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing,
distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and
indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third
party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the
article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright
holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Sato, Y., Shimizu-Inatsugi,
R., Takeda, K. _et al._ Reducing herbivory in mixed planting by genomic prediction of neighbor effects in the field. _Nat Commun_ 15, 8467 (2024). https://doi.org/10.1038/s41467-024-52374-7
Download citation * Received: 31 August 2023 * Accepted: 30 August 2024 * Published: 07 October 2024 * DOI: https://doi.org/10.1038/s41467-024-52374-7 SHARE THIS ARTICLE Anyone you share the
following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer
Nature SharedIt content-sharing initiative
