Reader TTS

ABSTRACT The rapid advancement of Industry 4.0 necessitates close collaboration among material research institutions to accelerate the development of novel materials. However,

multi-institutional cooperation faces significant challenges in protecting sensitive data, leading to data silos. Additionally, the heterogeneous and non-independent and identically

distributed (non-i.i.d.) nature of material data hinders model accuracy and generalization in collaborative computing. In this paper, we introduce the MatSwarm framework, built on swarm

learning, which integrates federated learning with blockchain technology. MatSwarm features two key innovations: a swarm transfer learning method with a regularization term to enhance the

alignment of local model parameters, and the use of Trusted Execution Environments (TEE) with Intel SGX for heightened security. These advancements significantly enhance accuracy,

generalization, and ensure data confidentiality throughout the model training and aggregation processes. Implemented within the National Material Data Management and Services (NMDMS)

platform, MatSwarm has successfully aggregated over 14 million material data entries from more than thirty research institutions across China. The framework has demonstrated superior

accuracy and generalization compared to models trained independently by individual institutions. SIMILAR CONTENT BEING VIEWED BY OTHERS THE COLLABORATIVE ROLE OF BLOCKCHAIN, ARTIFICIAL

INTELLIGENCE, AND INDUSTRIAL INTERNET OF THINGS IN DIGITALIZATION OF SMALL AND MEDIUM-SIZE ENTERPRISES Article Open access 30 January 2023 SWARM LEARNING FOR DECENTRALIZED AND CONFIDENTIAL

CLINICAL MACHINE LEARNING Article Open access 26 May 2021 DESIGN OF AN IMPROVED MODEL USING FEDERATED LEARNING AND LSTM AUTOENCODERS FOR SECURE AND TRANSPARENT BLOCKCHAIN NETWORK

TRANSACTIONS Article Open access 10 January 2025 INTRODUCTION The integration of Industrial Internet of Things (IIoT) and machine learning is revolutionizing research and development in

materials science1,2. The advent of Industry 4.0 has revolutionized materials science through the integration of IIoT. Advanced sensors and data acquisition technologies enable real-time

monitoring of material parameters such as temperature, hardness, melting point, and boiling point, providing unprecedented data support3. Concurrently, machine learning algorithms analyze

this vast data, allowing researchers to predict material properties, optimize designs, and discover new materials based on performance, structural properties, and preparatory conditions4,5.

However, creating accurate predictive models requires large, diverse training datasets. Today, various materials and big data platforms6,7,8 have been developed, providing researchers with

aggregated data. Nonetheless, for sensitive datasets that cannot be publicly shared, material data mining and analysis remain limited due to small sample sizes9,10. This poses a challenge

for training effective models. While data augmentation11,12 offers a potential solution, relying on simulated data can compromise model accuracy and generalization13,14. Additionally, even

with sufficient samples, standardized testing environments and methodologies can limit data diversity, further hindering model generalization for new materials. Transfer learning15 is often

used as a solution, but it involves sharing complete models with third parties, which raises concerns about data security and potential leakage. To accelerate the development of new

materials, a secure and collaborative computing methodology is essential. This approach must ensure data protection while allowing collaborative modeling across different organizations to

improve model accuracy and generalization. federated learning (FL)16 offers a viable solution by enabling organizations to collaborate without revealing their original data, sharing only

insights from local models. This protects sensitive data while allowing effective aggregation17. However, the traditional FL framework, which relies on a central server to aggregate local

model parameters18, raises concerns about the integrity and authenticity of the global model19. This centralization also makes the server susceptible to internal and external attacks20,21.

Moreover, most existing FL solutions have primarily been validated theoretically, using publicly available datasets and focusing on classification problems22,23. This theoretical focus fails

to address the practical challenges faced by non-i.i.d. datasets owned by different organizations, where issues of model accuracy and generalization are more pronounced. The lack of

empirical validation in real-world applications further questions the practicality and feasibility of these solutions. To truly harness the potential of FL in materials science, it is

crucial to develop methodologies that not only perform well in controlled, theoretical settings but also demonstrate robustness and effectiveness in diverse, real-world environments. This

will ensure the models are reliable, secure, and capable of advancing material discovery and development. To accelerate materials science research and development, building on the Materials

Genome Engineering (MGE) project24, we developed the NMDMS platform25,26 to facilitate the collection, storage, retrieval, and computation of material data. As the cornerstone of MGE’s data

applications, NMDMS platform provides data consumers with access to an extensive repository of material data contributed by over thirty research institutions across China. This platform also

serves as a data exchange and sharing hub for materials researchers. Although the NMDMS platform provides basic collaborative computing services, it lacks solutions for handling the

inherent limitations of FL in the context of material science. For example, while it achieves relatively high prediction accuracy for i.i.d. (independent and identically distributed)

training sets, it falls short in generalization capability for non-i.i.d. training sets and cannot ensure the confidentiality and integrity of parameters during the training process. Here,

we introduce MatSwarm as part of the NMDMS platform to address the limitations in materials science collaboration, particularly in the context of Industry 4.0, where efficient cooperation

among research institutions is crucial for accelerating novel material development. MatSwarm tackles the challenges posed by non-i.i.d. data and ensures the confidentiality and integrity of

sensitive material information through a decentralized collaborative computing framework. To the best of our knowledge, this application of the MatSwarm framework is unprecedented in the

materials field. Validated with real datasets from NMDMS, MatSwarm significantly enhances model training accuracy and generalization under heterogeneous data conditions. Additionally, by

integrating trusted execution environments (TEE) based on Intel SGX, the framework ensures secure and accurate model aggregations. Ultimately, MatSwarm not only addresses the collaborative

computing challenges but also unlocks the full potential of material data, driving innovation and meeting the demands of high-throughput computing and experimentation, thus accelerating

material discovery. A general introduction on MatSwarm is available in Supplementary Movie 1. RESULTS To date, the MatSwarm platform for material genome engineering (MGE) has collected over

14 million pieces of valid material data27. The platform predominantly encompasses data on special alloys, material thermodynamics/kinetics, composite functional materials, catalytic

materials, first-principles calculations, and biomedical materials. Data consumers from various fields can submit sharing tasks via the framework according to their specific needs, enabling

collaborative prediction of material properties and the development of new materials with other stakeholders. In our experiments, we utilize the prediction of perovskite formation energies

as an illustrative example to evaluate the performance of the MatSwarm framework. The following research questions (RQs) are addressed: * RQ 1: How does MatSwarm address security issues

during the collaborative computing process in the material science domain? * RQ 2: What are the advantages of MatSwarm compared to other methodologies within the MatSwarm? * RQ 3: How do

different factors affect the performance of MatSwarm, such as data distribution (non-i.i.d. vs i.i.d.), different local models and aggregation methods, and TEE? * RQ 4: How scalable is

MatSwarm in terms of its performance, including the size of the dataset, the number of features, and the number of participants? EXPERIMENTAL SETUP In this experiment, all services and

participants’ applications were deployed on cloud servers. The 16-core Intel Xeon (Ice Lake) Platinum 8369B processor with 32GB RAM (16GB as trusted RAM) was used to enable Intel ®Software

Guard Extensions, allowing organizations to employ enclaves for protecting the confidentiality and integrity of their code and data. The MatSwarm framework was implemented on a consortium

blockchain based on Hyperledger Fabric, with each node initiated as a Docker container and connected to the blockchain network using Docker Swarm28. Local models and aggregation methods are

available for participants to choose from on the MatSwarm platform. The batch size was set to 128, the number of iterations was 200, and the learning rate was 0.002. In the training

objective, _γ_ and _λ_ were set to 0.5 and 1, respectively. Dataset and Model Selection. In our experiments, we illustrate our approach using the prediction of perovskite formation energies

as a case study. We utilized perovskite data from our NMDMS platform to evaluate the performance of the MatSwarm framework, selecting 4016 perovskite samples. The training set consists of

3694 samples, evenly distributed among organizations. The test set comprises 322 samples. Detailed feature engineering on the dataset is described in Supplementary Note 4. Unless specified

otherwise, the number of participants in the experiment is set to three. This experiment aimed to test the performance of MatSwarm for non-i.i.d. material data. To this end, we divided the

training dataset into non-independent and identically distributed (non-i.i.d.) and independent and identically distributed (i.i.d.) datasets for comparative testing. For the non-i.i.d.

dataset, since the label values are normally distributed, we divided the training set into three datasets with different means and variances. The distribution of label values in these

datasets is illustrated in Supplementary Fig. 10. Regarding model selection, unless otherwise specified, the local training models utilize a Multilayer Perceptron (MLP) neural network for

training, with a hidden size of 32 and three network layers. On the MatSwarm framework, the task issuer can select different local training models and aggregation methods based on the

sharing task. For joint training, all organizations’ data was combined, and model training was also conducted using the MLP neural network. Evaluated Attacks. In this scenario, four nodes

participate in the collaborative task, with one acting as a Byzantine node launching the attack. Since all attack methods target the gradients, we modify the model updates in this experiment

to gradients instead of the model parameters. The aggregation methods include the five provided by the MatSwarm framework. We evaluate the impact of different attack methods on the accuracy

of these aggregation methods both inside and outside the TEE. Given the susceptibility of existing swarm learning frameworks to data poisoning attacks29, our experiment aims to demonstrate

the robustness of MatSwarm against such attacks. We consider the following popular poisoning attacks: * _Noise Attack_. The Byzantine nodes send noise-perturbed gradients generated by adding

Gaussian noise to the honest gradients30. We set the Gaussian distribution parameters as \({\mathbb{N}}(0.1,0.1)\). * _Label-Flipping_. The Byzantine nodes flip the local sample labels

during the training process to generate faulty gradients31. Specifically, a label _l_ is flipped as  − _l_, where _l_ is the formation energy of perovskite in our experiment. *

_Sign-Flipping_. During each round of learning, participants calculate the gradients ∇ _f__Θ_ of the local model, which are then uploaded to a central server for aggregation32. After

calculating the local gradients, the Byzantine nodes flip the signs of these gradients and send − ∇_f__Θ_. * _A Little is Enough_. The Byzantine nodes send malicious gradient vector with

elements crafted33. For each node _i_ ∈ [_d_ ], where _d_ is the number of Byzantine nodes, the Byzantine nodes calculate mean (_μ_i) and standard deviation (_σ_i) over benign updates, and

set corrupted updates _Δ_i to values in the range \(({\mu }_{{{{\rm{i}}}}}-{z}_{\max }{\sigma }_{{{{\rm{i}}}}},{\mu }_{{{{\rm{i}}}}}+{z}_{\max }{\sigma }_{{{{\rm{i}}}}})\), where \({z}_{\max

}\) ranges from 0 to 1. We set \({z}_{\max }=0.3\) in our experiment. * _Inner Product Manipulation_. The primary goal of IPM is to disrupt model performance by manipulating the inner

product of gradients to affect the direction and speed of model training34. For example, an attacker could enhance or diminish the effects of gradients in a particular dimension. We set the

scaling factor _α_ = 2, the gradient mean to be \(\overline{\nabla {f}_{{{{\boldsymbol{\theta }}}}}}\), and the gradient of the attack sent to be \(-\overline{\nabla

{f}_{{{{\boldsymbol{\theta }}}}}}*\alpha\). SECURITY ANALYSIS (RQ1) Confidentiality protection for local datasets: this framework enables collaborative computing among multiple organizations

while maintaining the confidentiality of local datasets. Traditional centralized machine learning methods require storing all datasets on a central server, posing risks of sensitive data

leakage. Through MatSwarm, each organization trains models on its local dataset without sharing the original data. Instead, organizations only share encrypted model parameters, not raw data.

This approach prevents the disclosure of sensitive information without disrupting the task processes of the participating organizations. Secure model training and aggregation based on TEE:

ensuring the security of model training processes during swarm learning is a significant challenge. To address this issue, MatSwarm employs a TEE established by Intel SGX. In this framework,

the original dataset is encrypted before being sent to the blockchain, using a shared key established through the Diffie-Hellman key exchange protocol. This ensures that data cannot be

stolen or tampered with during transmission. During model training and aggregation, the SGX Enclave performs these operations in a trusted execution environment, preventing attackers from

accessing or altering model parameters. Blockchain-based secure storage: this framework uses blockchain technology to replace untrusted third parties, significantly reducing the risk of data

leakage. Smart contracts are employed to standardize and automate model training and aggregation processes. Transactions are stored on the blockchain in hash form, and due to the uniqueness

of hash values, any tampering with transaction data will result in a change in the hash value. During the consensus process, nodes reject transactions with inconsistent hash values,

ensuring the integrity of global model storage and preventing network attacks. Additionally, digital signatures and hashes protect model updates, further enhancing the security of model

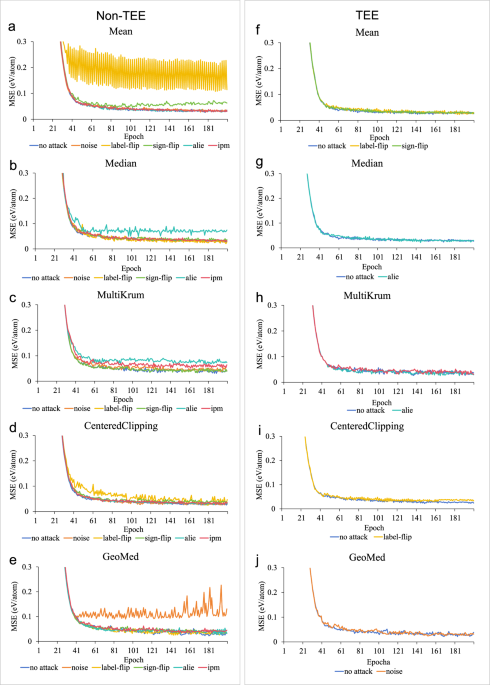
training and preventing tampering or contamination. Impact of attacks on different aggregation methods inside/outside TEE: as shown in Fig. 1a–e present test results in a non-TEE

environment. The results indicate that different aggregation methods, by design, can resist various data poisoning attacks. However, no single aggregation method can resist all types of data

poisoning attacks. The convergence speed and final model accuracy are affected to varying degrees depending on the specific attack and aggregation method used. To verify the TEE’s

resistance to data poisoning attacks, we tested the aggregation methods that were ineffective in the non-TEE within the TEE. Figure. 1f–j show that the TEE effectively resists all types of

data poisoning attacks. The convergence speed and model accuracy remain virtually unaffected, closely matching the performance observed in the absence of attacks. This demonstrates that

MatSwarm can effectively mitigate the risk of data poisoning attacks. METHODOLOGIES COMPARISON (RQ2) Within the MatSwarm framework, we conducted comparative experiments on prediction

accuracy and response time between MatSwarm, local independent training (referred to as “Solo”), joint data training (referred to as “Joint”), and other existing solutions, including

FedAvg35, FedProx36, Homomorphic Encryption Federated Transfer Learning (referred to as “HE-FTM”)37, and a similar framework proposed by Kalapaaking et al. (referred to as “Trust-FL”)38, to

illustrate the performance advantages of this framework. The performance comparison between MatSwarm and other methodologies is presented in Fig. 2. The results of model accuracy, evaluated

using mean squared error (MSE), are shown in Fig. 2. MatSwarm significantly improves prediction accuracy compared to Solo while maintaining the privacy of local datasets across various

organizations. Among the methodologies compared, MatSwarm achieves prediction accuracy closest to that of Joint, which can be considered the upper bound of accuracy for collaborative

computation. In contrast, HE-FTM involves polynomial approximation for evaluating nonlinear functions, resulting in some accuracy loss during training. Trust-FL, employing a horizontal FL

model, is more suited for i.i.d. training data and is less effective at predicting non-i.i.d. material data models. In terms of prediction accuracy, our model is more suitable for the

material science domain, demonstrating better prediction accuracy. Regarding response time, as shown in Fig. 2, Solo exhibits the shortest response time for each organization. Due to the

communication required between organizations, MatSwarm takes longer to execute compared to Solo and Joint. The average response time of MatSwarm increases by approximately 4 seconds compared

to Joint. Despite this increase, the security and privacy protection offered by MatSwarm are highly valuable. Moreover, in practical applications, organizations typically do not require

real-time model training, and the response time difference remains within an acceptable range. Notably, compared to HE-FTM, our model demonstrates lower computational complexity and

significantly improved response time. Compared to Trust-FL, our framework shows a slight increase in response time, primarily due to the enhanced security measures. Model training in our

framework occurs in a trusted execution environment, adding some communication overhead. Additionally, the blockchain consensus algorithm, inspired by PBFT, effectively addresses security

concerns arising from Byzantine nodes. Although the consensus algorithm slightly impacts response time by increasing communication frequency, the trade-off is justified by the improved

security performance. ABLATION EXPERIMENT (RQ3) To understand how different factors affect the performance of MatSwarm, we conducted ablation experiments varying data label distribution,

local model architectures, and w/wo a TEE. Unless specified otherwise, all local models use the same MLP architecture, and the aggregation algorithm is Mean. 1) non-i.i.d. VS i.i.d.: To

demonstrate the performance of the MatSwarm on non-i.i.d. material data, we tested both non-i.i.d. and i.i.d. datasets. * _i.i.d. Training Sets_: Fig. 3a depicts the prediction results for

perovskite formation energy using i.i.d. training sets selected independently for each organization. Our algorithm exhibits extremely high prediction accuracy for the i.i.d. dataset, nearing

the accuracy of Joint. * _Non-i.i.d. Training Sets_: As shown in Fig. 3b, the prediction accuracy for the non-i.i.d. dataset is slightly lower compared to the i.i.d. dataset but still close

to the accuracy of Joint. Compared to Solo, the accuracy for Org1 decreases due to the different label distributions between its data and the test set. A similar trend is observed for Org3.

However, as displayed in Table 1, using MatSwarm for predictions, the prediction MSE for Organization 1 decreased from 1.0291 to 0.2096, and for Organization 3, it decreased from 1.6159 to

0.5849, with the global model achieving an accuracy as low as 0.0903. Despite Organization 2 having a similar label distribution to the test set and thus showing good prediction accuracy,

its local model prediction accuracy also improved slightly after training with MatSwarm. This demonstrates that MatSwarm has strong generalization capabilities for non-i.i.d. material data.

2) Different local models and aggregation methods: Since MatSwarm will perform various training tasks beyond predicting perovskite formation energy, the choice of local models and

aggregation methods significantly impacts the accuracy of model training for different tasks. In this experiment, we compared the performance of MatSwarm using different local models and

aggregation methods to identify the most suitable collaborative computing scheme for predicting perovskite formation energy. The local models capable of solving regression problems include

MLP, recurrent neural network (RNN), Lasso, and long short-term memory (LSTM). The aggregation methods considered are Mean, Median, MultiKrum, CenteredClipping, and GeoMed. Ultimately, we

obtained the prediction results shown in Fig. 3c, d, and Table 1. The results indicate that using MLP within MatSwarm is the most suitable for predicting perovskite formation energy.

Building on the MLP local model architecture, we tested the impact of different aggregation methods on model accuracy and response time. In terms of accuracy, Mean and CenteredClipping

achieved the higher precision, while Mean was the most efficient in terms of response time. Therefore, to choose a suitable aggregation method, one should balance the trade-offs among the

needs of efficiency, accuracy, and security to achieve an optimal solution. This modular development approach facilitates participants in selecting the most suitable solutions for training

tasks and simplifies platform iterations and updates to meet diverse training demands in the material science domain. 3) non-TEE vs TEE: To evaluate the impact of TEE on the accuracy and

efficiency of the MatSwarm framework, we compared the MSE and response time of MatSwarm before and after using TEE. The comparison, shown in Fig. 4, indicates that using TEE does not

significantly affect the prediction accuracy of the model, whether training is conducted individually, with MatSwarm, or on joint data. However, the use of TEE introduces some communication

overhead, leading to an increase in response time. In the materials science domain, unlike in transaction systems, there is typically no strong demand for real-time response, and large model

training often takes hours. Therefore, the increase in response time due to TEE is negligible compared to the enhancement in security it provides. The TEE-based MatSwarm fully meets the

performance requirements for model prediction in the materials science field. SCALABILITY TESTING (RQ4) In this experiment, we evaluated the scalability of MatSwarm by examining the impact

of different dataset sizes, the number of features, and the number of participants. It is important to note that our NMDMS platform operates within a limited number of material

organizations. Currently, the platform accommodates up to 30 registered material organizations, with typically no >10 participants in a sharing task. Therefore, in our experiments, we

tested the framework with a maximum of 15 participants (material organizations). 1) Dataset size: Fig. 5a illustrates the MSE and response time of MatSwarm across varying dataset sizes. The

results indicate that dataset size has a negligible impact on the response time of MatSwarm, while the model accuracy continues to improve with increasing amounts of data. Notably, even when

each organization’s dataset comprises only 30% of the original dataset, our method demonstrates high accuracy. This indicates that our approach can achieve highly accurate training models

even with small sample sizes within each organization, effectively addressing the small sample problem in the materials science domain. 2) Number of features: as shown in Fig. 5b, increasing

the number of features does not significantly affect the response time of MatSwarm, demonstrating good scalability in terms of computational efficiency. In terms of prediction accuracy,

even with sample features constituting only 30% of the total features, our method achieves an MSE value as low as 0.155, indicating high accuracy. Therefore, using MatSwarm, even if each

organization can only obtain a limited number of feature values, it is still possible to achieve highly accurate training models. This makes our approach particularly effective for scenarios

where organizations have limited data or feature availability, ensuring robust and reliable model performance. Furthermore, after reaching ~90% of all features, the addition of less

important features does not substantially impact accuracy. In practical applications, selecting an appropriate set of features is crucial for balancing accuracy and efficiency, often

involving feature extraction optimization methods39,40. 3) Number of participants: as shown in Fig. 5c, the response time of MatSwarm increases linearly with the number of participants. This

increase is primarily due to the additional time required for communication and data coordination. The observed increase in response time aligns with theoretical expectations. In terms of

accuracy, the prediction accuracy of MatSwarm shows a notable upward trend as the number of participants increases. However, after a certain threshold, the accuracy may slightly decline due

to issues such as communication delays, data inconsistencies, and model overfitting introduced by a higher number of participants. Therefore, in the participant selection process, more is

not necessarily better. This demonstrates that MatSwarm can effectively learn the data characteristics of each organization, achieving highly accurate training models without the need for a

large number of participants for collaborative training. Consequently, this approach can also enhance the efficiency of model training. DISCUSSION ADVANTAGES OF THE MATSWARM FRAMEWORK

Security: MatSwarm incorporates advanced security measures to ensure data confidentiality and integrity. A key component of our security strategy is the use of TEEs, specifically Intel SGX,

which protect code and data from external attacks during computation. This approach effectively mitigates poisoning attacks associated with traditional FL setups. Furthermore, our

experimental setup included various attack scenarios to test the resilience of the MatSwarm framework. These tests demonstrated that MatSwarm effectively maintains data integrity and model

accuracy, even in the face of malicious attempts to corrupt the training process. Feasibility: MatSwarm is crucial for enabling collaborative computation over non-i.i.d. material data, a

common challenge due to the diverse nature of data sources and formats in this field. Compared to independent training by organizations and other FL methodologies, our method significantly

improves prediction accuracy and generalization ability. This highlights MatSwarm’s potential to unlock the full value of material data, facilitating more informed and accurate materials

discovery and development processes. Extensive testing with real-world data from the material science domain validated the usability of the MatSwarm framework. By engaging with actual

datasets from participating institutions, we demonstrated the feasibility and accuracy of the models generated through our platform. This use of real data underscores the framework’s ability

to address the ‘data silos’ problem prevalent in materials science. Scalability: MatSwarm has been rigorously tested across multiple dimensions, including varying dataset sizes, feature

quantities, and participant counts. The results show that the model maintains high and stable predictive accuracy, demonstrating excellent scalability and practical applicability. This

consistent performance, even with smaller sample sizes and fewer features, underscores MatSwarm’s capability to adapt to a broad range of scenarios. Such robustness enhances its potential

for widespread adoption in collaborative settings that require handling complex, heterogeneous data landscapes. Additionally, the MatSwarm platform utilizes a modular architecture, allowing

participants to select appropriate local models and aggregation methods based on their training tasks. As task demands increase, we will continuously iterate and update the platform’s local

models and aggregation methods. This approach aims to address various challenges in the material science domain, including performance prediction, material classification, and structural

optimization, ultimately creating a versatile collaborative computing platform. Adaptability: MatSwarm is a secure collaborative computing framework designed for non-public data across

organizations on the NMDMS, specifically addressing key regression challenges in the materials science domain. In this paper, we demonstrate the capabilities of the MatSwarm framework by

using it to predict perovskite formation energies, selecting a perovskite dataset as our example case. To be noted, our framework is suitable for general regression tasks within the

materials science domain, such as predicting the elastic properties of silicon materials and optimizing the microstructure of high-performance alloys. For each shared task, participants can

choose relevant datasets from their organization based on the task’s requirements. This ensures that the framework is not restricted to specific datasets during implementation; instead, it

dynamically adapts to select appropriate local datasets according to the specific needs of each task. Moreover, although MatSwarm is specifically designed for collaborative computing in the

materials science domain, its design principles can be leveraged by other domains with similar needs to construct their own swarm-based collaborative computing frameworks. For other domains

with similar application requirements, the framework can be adapted by modifying the objective function and selecting suitable local models and aggregation methods to fit specific needs.

Additionally, in Section 6 of the Supplementary Materials, we provide a detailed guide on how to extend and apply the MatSwarm framework to other domains. LIMITATIONS OF THE MATSWARM

FRAMEWORK Implementation complexity: while incorporating TEEs enhances security and privacy, it also increases the complexity of system setup and operations, necessitating robust

infrastructure and specialized expertise. To mitigate this, we provide detailed platform deployment and configuration documentation in the supplementary materials, which stakeholders can use

to deploy new training tasks on this platform. Potential latency issues: the decentralized nature of blockchain and remote attestation based on TEEs can introduce delays in model training

and aggregation. However, in the field of materials science, real-time requirements for training are not stringent. The minor increase in latency is negligible compared to the benefits of

resolving the issue of data silos in material data. Hardware dependency: dependence on TEEs, such as Intel SGX, to protect data during computation may limit the applicability of our

framework in environments without such hardware support. Nevertheless, our demonstration system offers the option to choose whether to use TEEs to secure the confidentiality of the model

aggregation process. Even without TEE protection, data security during transmission is ensured through data encryption and secure communication channels. In the future, we plan to offer

additional privacy protection technologies, such as homomorphic encryption and differential privacy, to support a broader range of application scenarios. METHODS OVERALL ARCHITECTURE OF

MATSWARM In this section, we present our proposed framework, MatSwarm, designed for the secure sharing of material big data using swarm transfer learning combined with TEEs. Table 2

summarizes the critical symbols used in our framework. The organizations illustrated in Fig. 6 represent examples of entities involved in materials science. It is noteworthy that our

MatSwarm framework is primarily used to address challenges in collaborative computing within the domain of materials science, as evidenced by its application to a regression problem, such as

predicting material properties like perovskite formation energies, as discussed in this paper. Nevertheless, the framework possesses the potential for extension and application in other

fields facing analogous collaborative computing challenges. Further elaboration on this aspect can be found in Supplementary Note 5. The MatSwarm framework enables collaborative computing

tasks between material organizations. As depicted in Fig. 6, MatSwarm involves multiple organizations (denoted as _N_) collaborating to execute shared tasks. Each organization is responsible

for training its own local models. The blockchain nodes provide a distributed computing environment for the participating organizations and store aggregated models. Additionally, the

trusted execution environment ensures the secure aggregation of local model parameters and collaborates with the blockchain to generate the swarm global model. * 1. Organizations: within the

MatSwarm framework, organization _O_i (1 ≤ _i_ ≤ _N_) collaboratively trains models to meet shared material performance prediction requirements. Initially, each organization conducts

material features sampling locally, and the collected samples are stored as local datasets on their respective cloud servers. Subsequently, organizations choose an appropriate machine

learning method to train a local model. To ensure security during model training, each organization deploys at least one blockchain node on an Intel SGX-enabled cloud server, and the local

model training is performed in SGX’s application enclave. This setup establishes encrypted and authenticated channels, allowing sensitive data to be securely transferred between the cloud

server and the Intel SGX Enclave. * 2. Blockchain Network: MatSwarm leverages the decentralized nature of blockchain to create a collaborative computing environment. Each organization joins

the blockchain network at local blockchain nodes. Within the MatSwarm framework, three transaction types are defined: retrieval, sharing, and uploading. The retrieval transaction verifies

the existence of relevant sharing global models on the blockchain before initiating a new sharing task. The sharing transactions involve organizations initiating new tasks, such as material

performance prediction, with the option for other organizations to participate. The uploading transactions store the final global model on the blockchain, ensuring its integrity and

preventing tampering, thus facilitating model retrieval and usage by other organizations. * 3. Trusted Execution Environment: the TEE, implemented via Intel SGX, ensures the confidentiality

and integrity of local and global models. Each organization applies for two Application Enclaves (denoted as AE) in SGX. AE1 is used to load encrypted local datasets and execute local

models, ensuring confidentiality and integrity during execution. AE2 is used to aggregate global models. This approach ensures the integrity of model aggregation, with all organizations

automatically executing the same model aggregation code through smart contracts41 in AE2. Smart contracts automate the enforcement and management of agreed-upon processes and conditions,

ensuring consistent execution, eliminating discrepancies, enhancing security, and reducing reliance on third-party intermediaries. Additionally, the Quoting Enclave (denoted as QE) generate

attestation REPORT R to assist in remote authentication between AEs in various organizations. PROBLEM FORMULATION We consider a MatSwarm framework constructed by _N_(_N_ > 2)

organizations, where _K_(_K_ ≤ _N_) organizations are in a sharing task, each possessing a local dataset DLi, ∀ _i_ ∈ _K_. Each organization maintains a local model

\({f}_{{{{{\boldsymbol{\theta }}}}}_{{{{\rm{i}}}}}}:{{{{\bf{X}}}}}_{{{{\rm{i}}}}}\to {y}_{{{{{\rm{pre}}}}}_{{{{\rm{i}}}}}}\) with parameters _Θ_i, where Xi and

\({y}_{{{{{\rm{pre}}}}}_{{{{\rm{i}}}}}}\) denote the input and output spaces, respectively. In our study, we assume that all organizations have the same input/output specifications and

homogeneous local model architectures. However, they may choose different local models and aggregation methods based on the sharing task. The objective is to collaboratively train the local

models to ensure that each generalizes well on the joint data distribution, thereby improving prediction accuracy for non-i.d.d. material data. To achieve this objective, we propose a swarm

transfer learning method within the MatSwarm framework. The core of our method is to identify invariances between resource-rich source domains and resource-scarce target domains,

facilitating the learning of common representation spaces and enabling knowledge transfer across domains. The objective function reveals that during the swarm transfer learning process

between organization _O_i and organization _O_i+1, local model training is interdependent, necessitating the exchange of intermediate training results. The training process adheres to a

linear cycle method, with sequential training conducted between organizations in the order [_O_1→_O_2→. . .→_O_K→_O_1]. The completion of training between organizations _O_K and _O_1

signifies the end of a local training round. After each round of local model parameter updates, the parameters are aggregated, and the updated global model parameters are sent back to each

organization for the next round of local model updates. This iterative process continues until the model converges to a specified threshold. The training objective is typically formulated as

the following algorithm: $${\min}_{{{{{\boldsymbol{\theta

}}}}}_{{{{\rm{i}}}},{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K}}f({{{{\bf{X}}}}}_{{{{\rm{i}}}},{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K},{y}_{{{{\rm{i}}}}{{\mathrm{mod}}}\,K})=

{\sum}_{{{{\rm{i=1}}}}}^{{{{\rm{K}}}}}{{{{\mathscr{L}}}}}_{1}({{{{\bf{X}}}}}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K},{y}_{{{{\rm{i}}}}{{\mathrm{mod}}}\,K})+\gamma

{{{{\mathscr{L}}}}}_{2}({{{{\bf{X}}}}}_{{{{\rm{i}}}},{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K})\\ +\frac{\lambda }{2}\left(\parallel {{{{\boldsymbol{\theta }}}}}_{{{{\rm{i}}}} \,

{{\mathrm{mod}}}\,K}{\parallel }^{2}+\parallel {{{{\boldsymbol{\theta }}}}}_{{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K}{\parallel }^{2}\right)$$ (1)

$${{{{\mathscr{L}}}}}_{1}({{{{\bf{X}}}}}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K},{y}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K})={({y}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K}-\varphi

({{{{\bf{X}}}}}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K}))}^{2}$$ (2) $${{{{\mathscr{L}}}}}_{2}({{{{\bf{X}}}}}_{{{{\rm{i}}}},{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K})={\left\Vert {u}_{{{{\rm{i}}}} \,

{{\mathrm{mod}}}\,K}({{{{\bf{X}}}}}_{{{{\rm{i}}}} \, {{\mathrm{mod}}}\,K})-{u}_{{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K}({{{{\bf{X}}}}}_{{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K})\right\Vert }_{F}^{2}$$

(3) The loss function in Equation (1) is formulated to optimize the parameters _Θ_. It aims to minimize the overall loss by integrating multiple components, including

\({{{{\mathscr{L}}}}}_{1}\), \({{{{\mathscr{L}}}}}_{2}\), and regularization terms. \({{{{\mathscr{L}}}}}_{1}\): This term represents the first component of the loss function, capturing the

discrepancy between the predicted outputs and the true labels. Specifically, \({y}_{{{{\rm{i}}}}{{\mathrm{mod}}}\,K}\) denotes the label of organization _O__i_. The form of the objective

function _φ_ depends on the nature of the sharing task, such as classification or regression, and the chosen local model. \({{{{\mathscr{L}}}}}_{2}\): The term \({{{{\mathscr{L}}}}}_{2}\)

typically corresponds to a regularization technique, such as L2 regularization, which helps prevent overfitting and promotes model generalization, where _u_ denotes the representation

converted from the original data, and \(\parallel \cdot {\parallel }_{F}^{2}\) refers to the square of the Frobenius norm. It penalizes large parameter values to create a more balanced and

robust model. _γ_: This parameter _γ_ represents the weight assigned to the \({{{{\mathscr{L}}}}}_{2}\) component in the overall loss function. Adjusting _γ_ controls the trade-off between

fitting the training data and applying regularization. _λ_: The parameter _λ_ determines the weight assigned to the regularization terms that penalize the magnitude of the parameters

\({{{{\boldsymbol{\theta }}}}}_{{{{\rm{i}}}}{{\mathrm{mod}}}\,K}\) and \({{{{\boldsymbol{\theta }}}}}_{{{{\rm{i}}}}+1{{\mathrm{mod}}}\,K}\). It controls the strength of the regularization,

helping manage the model’s complexity. Based on the above illustration, Equation (1) represents a combined loss function designed to optimize the parameters _Θ_. This function integrates the

task-specific loss \({{{{\mathscr{L}}}}}_{1}\), a regularization term \({{{{\mathscr{L}}}}}_{2}\), and a regularization of parameter magnitudes. The components are weighted by _γ_ and _λ_

to achieve a balance between data fitting and model complexity control. To ensure the confidentiality and integrity of the local model and global model generation, MatSwarm incorporates TEE

utilizing Intel SGX. Each organization’s cloud server is enabled with Intel SGX and includes _M_(_M_ ≥ _N_) blockchain nodes within the blockchain network. Each organization can deploy

multiple blockchain nodes. To facilitate understanding, we assume that each organization has deployed a single blockchain node, denoted as BNi (_i_ ≤ _M_). The blockchain node BNi must be

deployed on an Intel SGX-enabled cloud server. To train local and global models, each organization requests the creation of two AEs. AE1 is used to load encrypted local datasets and smart

contract SC1 for training local models. AE2 is used to load encrypted local model parameters and smart contract SC2 for aggregating local model parameters. WORKING MECHANISMS The overall

working mechanism of MatSwarm includes three main stages: task submission, task execution, and task archive. Videos on the procedures and operations of MatSwarm are available as

Supplementary Movies 2 and 3. 1) Task Submission: assume that all material organizations willing to conduct joint model training have registered and stored their metadata on the blockchain.

Organization _O_1, as the task issuer among participants, initiates a retrieval transaction request to the local blockchain node with a task information digest. The local blockchain node

retrieves the blockchain history to determine whether an archived task related to the task information digest has been generated. If such a task exists, the corresponding retrieval result is

returned. If organization _O_1 does not obtain retrieval results for the archived task, it will retrieve the metadata of organizations from the blockchain. Once the task issuer identifies

the organizations to be invited, it will design the sharing task scheme, including the task description, metadata description, and the selection of local models and aggregation methods. The

task issuer subsequently initiates a sharing transaction request to organizations with relevant datasets to join the sharing task as participants. The blockchain nodes of participating

organizations become active nodes, while those of non-participating organizations remain passive. The active nodes participate in the global model consensus mechanism for the task. 2) Task

Execution: to facilitate model aggregation, it is essential to standardize the structure and format of the input datasets among participants. The task issuer should create a virtual dataset

and broadcast it to the blockchain network, enabling each participant to align their local datasets with the standardized format. Subsequently, participants can use their standardized

datasets to train their local models. The task issuer trains a local model and deploys the code into Smart Contract 1 (SC1) running in its AE1. Other participants can invoke SC1 via the

blockchain to train their local models in a similar manner, ensuring uniformity in the local model training code. After each round of local model training, remote attestation is required

between the AE1 of each participant to verify the credibility of the remote nodes and the integrity and confidentiality of the local model. Following remote attestation, encrypted local

models are shared among organizations to generate the global model. To ensure the integrity and confidentiality of the aggregation process, each organization’s blockchain node performs model

aggregation in its AE2. The steps involved are as follows: the task issuer deploys the aggregation algorithm onto the smart contract SC2 running in the AE2. Other participants invoke SC2

from the blockchain, subsequently loading the smart contract and encrypted local model sets submitted by others into their respective AE2. Each participant’s AE2 independently aggregates the

models to generate a global model. To ensure the credibility of each organization’s AE2 and the integrity of the global model, the blockchain network must receive all attestation reports

generated by each organization’s AE2. Consequently, the blockchain nodes complete remote attestation through a consensus mechanism. 3) Task Archive: during each round of training,

organizations obtain the current global model and use it to update their local model until the loss function converges to a specific threshold. However, before a credible global model is

ultimately generated, a consensus must be reached among participants. Once a consensus is achieved, the global model is stored on the blockchain to prevent tampering. Therefore, participants

must ensure that the final global model is recognized by all participants through a consensus mechanism. The model is then securely stored for future retrieval and use. LOCAL MODEL

GENERATION The initial step in local model training involves loading the encrypted local dataset. To ensure security, Intel SGX’s AE only accepts encrypted data. Therefore, before sending

the local dataset DLi to the local AE1, the blockchain node _B__N__i_ must encrypt it using a symmetric encryption algorithm such as advanced encryption standard (AES)42 or Triple Data

Encryption Standard43, represented as Er(. , Kr). Symmetric encryption and decryption between BNi and its AE1 are performed using the key Kri. This process is denoted as Er(. , Kri). The key

Er(. , Kr) is transmitted through a secure channel established by the Diffie-Hellman key exchange protocol44, which allows two parties to establish a shared secret over an unsecured

communication channel, providing a foundation for encrypting further communications. BNi generates an encrypted local dataset Er(DLi, Kri) and sends it to _A__E_1. Upon receipt, AE1 uses the

key Kri to decrypt Er(DLi, Kri)(1 ≤ _i_ ≤ _M_), obtaining the plaintext DLi of the local dataset. This process can be represented as BNi∣Er(DLi, Kri) → AE1∣Dr(Er(DLi, Kri), Kri). The second

step involves local model training. Organizations deploy the local model using the smart contract SC1 to train their local datasets in AE1. For local model training, participants on our

platform can select the appropriate machine learning model based on their task requirements, including MLP45, Lasso46, RNN47, and LSTM48. As the platform evolves, it will offer a broader

range of local training models to meet diverse task requirements. In this paper, we demonstrate the local model training process using an example of predicting perovskite formation energy,

employing the MLP neural network for local model training and the stochastic gradient descent algorithm for parameter updating. As shown in Fig. 7, consider the training between organization

_O_1 and organization _O_2 as an example. Organization _O_2 calculates intermediate results and encrypts them with the public key PKIAS from Intel Authentication Service (IAS). The

encrypted intermediate results \({[{{{{\bf{u}}}}}_{2}^{{{{\rm{t}}}}}]}_{{{{{\bf{PK}}}}}_{{{{\rm{IAS}}}}}}\) and

\({[{{{{\boldsymbol{\theta}}}}}_{2}^{{{{\rm{t}}}}}]}_{{{{{\bf{PK}}}}}_{{{{\rm{IAS}}}}}}\) are sent to organization _O_1. The organization _O_1 decrypts the intermediate results using the

private key PRIAS and calculates the local model gradient \(\frac{\partial {{{{\mathscr{L}}}}}_{1}^{{{{\rm{t}}}}}}{\partial {{\boldsymbol{\theta}} }_{1}^{{{{\rm{t}}}}}}\) and loss function

\({{{{\mathscr{L}}}}}_{1}^{{{{\rm{t}}}}}\). Similarly, organization _O_1 calculates a set of intermediate results, encrypts them with the public key PKIAS, and sends the encrypted

intermediate results \({[{{{{\boldsymbol{\theta }}}}}_{1}^{{{{\rm{t}}}}}]}_{{{{{\bf{PK}}}}}_{{{{\rm{IAS}}}}}}\) and

\({[{{{{\bf{u}}}}}_{1}^{{{{\rm{t}}}}}]}_{{{{{\bf{PK}}}}}_{{{{\rm{IAS}}}}}}\) are sent to organization _O_2, which then calculates the local model gradient \(\frac{\partial

{{{{\mathscr{L}}}}}_{2}^{{{{\rm{t}}}}}}{\partial {{{{\boldsymbol{\theta }}}}}_{2}^{{{{\rm{t}}}}}}\) and loss function \({{{{\mathscr{L}}}}}_{2}^{t}\). Both organizations update their local

model parameters \({{{{\boldsymbol{\theta }}}}}_{1}^{{{{\rm{t+1}}}}}\) and \({{\boldsymbol{\theta }}}_{2}^{{{{\rm{t+1}}}}}\) using the calculated local model gradients. After each

organization completes this round of local model training, the blockchain nodes of each organization perform remote certification of all AE1 through a consensus mechanism. Subsequently,

organizations encrypt and share the updated local model parameters \({{{{\boldsymbol{\theta }}}}}_{i}^{{{{\rm{t+1}}}}}\) with other participants to aggregate local model parameters for the

current round. GLOBAL MODEL GENERATION This section will elaborate on generating global models, covering crucial aspects such as smart contract deployment, model aggregation, remote

attestation, and consensus mechanisms. Figure 8 illustrates the process of global model generation. 1) Smart contract deployment: the task issuer _O_1 deploys the model aggregation algorithm

to the blockchain via the local blockchain node BN1 as a smart contract. Each participant can retrieve and invoke the smart contract from the blockchain. The blockchain node BNi loads the

smart contract and encrypted local model parameter set \({[[{{{{\bf{M}}}}}_{{{{\rm{L}}}}}^{{{{\rm{t}}}}}]]}_{{{{{\bf{PK}}}}}_{IAS}}\) into AE2 of TEEi. The parameters are then decrypted

using PRIAS to construct the plaintext of the local model parameter set \({{{{\bf{M}}}}}_{{{{\rm{L}}}}}^{{{{\rm{t}}}}}=\left({{{{\boldsymbol{\theta

}}}}}_{1}^{{{{\rm{t}}}}},{{{{\boldsymbol{\theta }}}}}_{{{{\rm{2}}}}}^{{{{\rm{t}}}}},\cdots \,,{{{{\boldsymbol{\theta }}}}}_{{{{\rm{K}}}}}^{{{{\rm{t}}}}}\right)\). The calculation of global

model parameters occurs in AE2 of TEEi to ensure the confidentiality of sensitive parameters. Smart contracts facilitate the transfer of global model parameters. 2) Model aggregation: the

global model parameters \({{{{\bf{M}}}}}_{{{{\rm{G}}}}}^{{{{\rm{t+1}}}}}\) calculated in each participant’s AE2 are given by:

$${{{{\bf{M}}}}}_{{{{\rm{G}}}}}^{{{{\rm{t+1}}}}}={\sum}_{i=1}^{K}\frac{| {{{{\rm{DL}}}}}_{{{{\rm{i}}}}}| }{n}{{{{\bf{M}}}}}_{{{{{\rm{L}}}}}_{{{{\rm{i}}}}}}^{{{{\rm{t}}}}},n={\sum}_{i=1}^{K}|

{{{{\rm{DL}}}}}_{{{{\rm{i}}}}}|$$ (4) where \({{{{\bf{M}}}}}_{{{{\rm{G}}}}}^{{{{\rm{t+1}}}}}\) represents the global model updated in the _t_ + 1 round, _K_ denotes the number of

participants, ∣DLi∣ represents the number of samples used by the _i_-th participant to train the local model, and _n_ is the total number of samples used to train all local models.

\({{{{\bf{M}}}}}_{{{{{\rm{L}}}}}_{{{{\rm{i}}}}}}^{{{{\rm{t}}}}}\) is the local model parameters set updated by the _i_-th participant in the _t_ rounds. Notably, parameter aggregation is

illustrated using the Mean method35 in MatSwarm, which is the most widely used approach. However, various aggregation methods are available, such as MultiKrum49, CenteredClipping50,

GeoMed51, and Median52, among others. On our platform, participants can choose different model aggregation methods based on task requirements and robustness needs. 3) Remote attestation:

during the global model generation process, remote attestation is used to verify the integrity of the global model generated by AE2. In this method, the blockchain node BNi facilitates

interaction between the AE2 of TEEi and the blockchain network, serving as both an aggregator and verifier in the attestation process. TEEi generates a REPORT structure information Ri

containing the current enclave identity information Mi, and other metadata through the EREPORT function, and signs Ri to produce a Message Authentication Code (MAC) tag MACi. AE2 sends Ri

and MAC tags to the Quoting Enclave in TEEi for mutual attestation. The Quoting Enclave calls the EGETKEY command to decrypt the MACi and verifies the decrypted information against Ri. After

successful mutual attestation within TEEi, the Quoting Enclave uses the private key (AKRi) of the attestation key generated by the Intel Provisioning Service’s Provisioning Seal Key, to

sign Ri and create a Quote QGi = Sign(Ri, AKRi). Only Quoting Enclave can access the key used for attestation in the Intel Provisioning Service to verify the credibility of TEEi. The QGi is

then sent through the blockchain network to the blockchain nodes of other participants for verification. Once BNi receives K-1 Quotes, it will verify each Quote using the public key AKPi

generated by the Intel Provisioning Service. The verification is completed utilizing the function _v__e__r__i__f__y_(Sign(QGi, AKRi), AKPi). Once the Quote is validated, BNi will extract the

global model

\({{{{\bf{M}}}}}_{{{{\rm{G}}}}}^{{{{\rm{t+1}}}}}\)=\(\left({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{1}}}}}}^{{{{\rm{t+1}}}}},{{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{2}}}}}}^{{{{\rm{t+1}}}}},\ldots,{{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{K}}}}}}^{{{{\rm{t+1}}}}}\right)\)

from QG = \(\left({{{{\bf{QG}}}}}_{1},{{{{\bf{QG}}}}}_{2},\ldots,{{{{\bf{QG}}}}}_{{{{\rm{K}}}}}\right)\) for subsequent consensus. 4) Global Model Consensus: at this stage, the consensus

mechanism is used to determine the global model accepted by the participants. We use the PBFT53 consensus, which can tolerate _f_ Byzantine fault nodes. We assume that three organizations

are participating in the shared task. The blockchain node BN1 is a blockchain node of the task issuer _O_1 acting as the primary node; BN2 and BN3 are blockchain nodes of the other two

participants _O_2 and _O_3 participating in the consensus mechanism as active nodes; BNj (_j_ ∈ _M_) denotes the blockchain node of organizations that are not participating in the sharing

task, referred to as passive nodes. The consensus mechanism consists of five steps: request, pre-prepare, prepare, commit, and reply. Request phase: the task issuer _O_1 initiates a global

model consensus request to the deployed blockchain node BN1. Pre-prepare stage: BN1 calculates

Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{1}}}}}}^{{{{\rm{t+1}}}}},{{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{2}}}}}}^{{{{\rm{t+1}}}}},\ldots,{{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{K}}}}}}^{{{{\rm{t+1}}}}})\)

and broadcasts Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{1}}}}}}^{{{{\rm{t+1}}}}})\) to BN2 and BN3 if the Hash of all global models is equal. Prepare stage: after receiving the

Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{1}}}}}}^{{{{\rm{t+1}}}}})\) sent by BN1, BN2, and BN3, calculate the Hash value of the global model

\({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{i}}}}}}^{{{{\rm{t+1}}}}}(1\le i\le K)\) sent by each organization. If all hash values are equal to

Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{1}}}}}}^{{{{\rm{t+1}}}}})\), BN2 and BN3 broadcast Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{2}}}}}}^{{{{\rm{t+1}}}}})\) and

Hash\(({{{{\bf{M}}}}}_{{{{{\rm{G}}}}}_{{{{\rm{3}}}}}}^{{{{\rm{t+1}}}}})\) to the other two participants, respectively. Commit stage: after receiving the calculation results from the other

nodes, all participants verify whether a consistent global model has been agreed upon by all. If consensus is achieved, they broadcast confirmation messages to the other participants. Reply

stage: the consensus request is considered complete when each participant receives confirmation messages from at least two-thirds of the nodes. A Reply message is then constructed and sent

to _O_1. Once _O_1 receives confirmation messages from more than two-thirds of the nodes, it finalizes the global model and broadcasts its hash to all active and passive nodes for storage.

The processes of local and global model generation are repeated round and round until the model converges to a threshold. In the end, the final global model is stored on the blockchain,

ensuring tamper resistance while facilitating efficient retrieval by others. REPORTING SUMMARY Further information on research design is available in the Nature Portfolio Reporting Summary

linked to this article. DATA AVAILABILITY All datasets used are publicly available at https://github.com/SICC-Group/MatSwarm.git and Zenodo54. All data supporting the findings described in

this manuscript are available in the article and in the Supplementary Information and from the corresponding author upon request. Source data are provided with this paper. CODE AVAILABILITY

The codes are available in open source at https://github.com/SICC-Group/MatSwarm.git and Zenodo54. REFERENCES * Liu, C. et al. A transfer learning cnn-lstm network-based production progress

prediction approach in iiot-enabled manufacturing. _Int. J. Prod. Res._ 61, 4045–4068 (2023). Article  Google Scholar  * Chaudry, U. M., Hamad, K. & Abuhmed, T. Machine learning-aided

design of aluminum alloys with high performance. _Mater. Today Commun._ 26, 897 (2021). Google Scholar  * Malik, P. K. et al. Industrial internet of things and its applications in industry

4. _Comput. Commun._ 166, 125–139 (2021). Article  Google Scholar  * Damewood, J. et al. Representations of materials for machine learning. _Annu. Rev. Mater. Res._ 53, 399–426 (2023).

Article  ADS  CAS  Google Scholar  * Stergiou, K. et al. Enhancing property prediction and process optimization in building materials through machine learning: a review. _Comput. Mater.

Sci._ 220, 031 (2023). Article  Google Scholar  * Aflow - Automatic FLOW for materials discovery. https://aflowlib.org/ (2024). * Crystallography open database.

http://www.crystallography.net/cod/ (2024). * Materials data repository home. https://materialsdata.nist.gov/. (2024). * Morgan, D. & Jacobs, R. Opportunities and challenges for machine

learning in materials science. _Annu. Rev. Mater. Res._ 50, 71–103 (2020). Article  ADS  CAS  Google Scholar  * Xu, P., Ji, X., Li, M. & Lu, W. Small data machine learning in materials

science. _npj Comput. Mater._ 9, 42 (2023). Article  ADS  Google Scholar  * Kim, Y. et al. Deep learning framework for material design space exploration using active transfer learning and

data augmentation. _npj Comput. Mater._ 7, 140 (2021). Article  ADS  Google Scholar  * Jain, S., Seth, G., Paruthi, A., Soni, U. & Kumar, G. Synthetic data augmentation for surface

defect detection and classification using deep learning. _J. Intell. Manuf._ 33, 1007–1020 (2022). Article  Google Scholar  * Hnewa, M. & Radha, H. Object detection under rainy

conditions for autonomous vehicles: a review of state-of-the-art and emerging techniques. _IEEE Signal Process. Mag._ 38, 53–67 (2020). Article  Google Scholar  * Wen, Y., Tran, D.,

Izmailov, P., Wilson, A.G. Combining ensembles and data augmentatio.n can harm your calibration. _In_: International Conference on Learning Representations https://arxiv.org/abs/2010.09875

(2021). * Lejeune, E. & Zhao, B. Exploring the potential of transfer learning for metamodels of heterogeneous material deformation. _J. Mech. Behav. Biomed. Mater._ 117, 104,276 (2021).

Article  CAS  Google Scholar  * Zhang, C. et al. A survey on federated learning. _Knowl. Based Syst._ 216, 106,775 (2021). Article  Google Scholar  * Mothukuri, V. et al. A survey on

security and privacy of federated learning. _Future Gener. Comput. Syst._ 115, 619–640 (2021). Article  Google Scholar  * Kairouz, P. et al. Advances and open problems in federated learning.

_Found. Trends Mach. Learn._ 14, 1–210 (2021). Article  Google Scholar  * Zhang, J. et al. Security and privacy threats to federated learning: Issues, methods, and challenges. _Secur.

Commun. Netw._ 2022 (2022). * Tolpegin, V., Truex, S., Gursoy, M.E., Liu, L. Data poisoning attacks against federated learning systems. _In_: Computer Security–ESORICS 2020: 25th European

Symposium on Research in Computer Security, pp. 480–501 (2020). * Xiao, X., Tang, Z., Li, C., Xiao, B. & Li, K. Sca: sybil-based collusion attacks of iiot data poisoning in federated

learning. _IEEE Trans. Ind. Inform._ 19, 2608–2618 (2022). Article  Google Scholar  * Bakopoulou, E., Tillman, B. & Markopoulou, A. Fedpacket: a federated learning approach to mobile

packet classification. _IEEE Trans. Mob. Comput._ 21, 3609–3628 (2021). Article  Google Scholar  * Wang, B., Li, A., Pang, M., Li, H., Chen, Y. Graphfl: a federated learning framework for

semi-supervised node classification on graphs. _In_: 2022 IEEE International Conference on Data Mining (ICDM) pp. 498–507 (2022). * Xie, J., Su, Y., Zhang, D. & Feng, Q. A vision of

materials genome engineering in china. _Engineering_ 10, 10–12 (2022). Article  Google Scholar  * Wang, R. et al. A secured big-data sharing platform for materials genome engineering:

state-of-the-art, challenges and architecture. _Future Gener. Comput. Syst._ 142, 59–74 (2023). Article  Google Scholar  * Wang, R., Xu, C., Ye, F., Tang, S., Zhang, X., S-mbda: a

blockchain-based architecture for secure storage and sharing of material big-data. _IEEE Internet Things J_. 11, 15 (2024). * Liu, S. et al. An infrastructure with user-centered presentation

data model for integrated management of materials data and services. _npj Comput. Mater._ 7, 88 (2021). Article  ADS  CAS  Google Scholar  * Ileana, M., Oproiu, M.I., C.V., Marian, Using

docker swarm to improve performance in distributed web systems. _In_: International Conference on Development and Application Systems (DAS) pp. 1–6 (2024). * Jere, M. S., Farnan, T. &

Koushanfar, F. A taxonomy of attacks on federated learning. _IEEE Secur. Priv._ 19, 20–28 (2020). Article  Google Scholar  * Romano, Y., Aberdam, A., Sulam, J. & Elad, M. Adversarial

noise attacks of deep learning architectures: stability analysis via sparse-modeled signals. _J. Math. Imaging Vis._ 62, 313–327 (2020). Article  MathSciNet  Google Scholar  * Fang, M., Cao,

X., Jia, J., Gong, N., Local model poisoning attacks to byzantine-robust federated learning. 29th USENIX security symposium (USENIX Security 20), pp. 1605–1622 (2020). * Li, L., Xu, W.,

Chen, T., Giannakis, G. B. & Ling, Q. Rsa: Byzantine-robust stochastic aggregation methods for distributed learning from heterogeneous datasets. _Proc. AAAI Conf. Artif. Intell._ 33,

1544–1551 (2019). Google Scholar  * Baruch, G., Baruch, M., Goldberg, Y., A little is enough: circumventing defenses for distributed learning. _Adv. Neural Inf. Process. Syst._, 32 (2019). *

Xie, C., Koyejo, O., Gupta, I. Fall of empires: breaking byzantine-tolerant SGD by inner product manipulation. https://arxiv.org/abs/1903.03936 (2020). * Li, X., Huang, K., Yang, W., Wang,

S., Zhang, Z. On the convergence of fedavg on non-iid data. _In_: International Conference on Learning Representations, https://openreview.net/forum?id=HJxNAnVtDS (2020). * Li, T. et al.

Federated optimization in heterogeneous networks. _Proc. Mach. Learn. Syst._ 2, 429–450 (2020). Google Scholar  * Liu, Y., Kang, Y., Xing, C., Chen, T. & Yang, Q. Secure federated

transfer learning. _IEEE Intell. Syst._ 35, 70–82 (2020). Article  Google Scholar  * Kalapaaking, A. P. et al. Blockchain-based federated learning with secure aggregation in trusted

execution environment for internet-of-things. _IEEE Trans. Ind. Inform._ 19, 1703–1714 (2022). Article  Google Scholar  * Chowdhury, S., Mayilvahanan, P. & Govindaraj, R. Optimal feature

extraction and classification-oriented medical insurance prediction model: machine learning integrated with the internet of things. _Int. J. Comput. Appl._ 44, 278–290 (2022). Google

Scholar  * Fatani, A., Dahou, A., Al-Qaness, M. A., Lu, S. & Abd Elaziz, M. Advanced feature extraction and selection approach using deep learning and aquila optimizer for iot intrusion

detection system. _Sensors_ 22, 140 (2022). Article  ADS  Google Scholar  * Hewa, T., Ylianttila, M. & Liyanage, M. Survey on blockchain based smart contracts: applications,

opportunities and challenges. _J. Netw. Comput. Appl._ 177, 102,857 (2021). Article  Google Scholar  * Daemen, J. & Rijmen, V. Reijndael: the advanced encryption standard. _Dobb’s. J._

26, 137–139 (2001). Google Scholar  * Barker, E., Mouha, N. Recommendation for the triple data encryption algorithm (tdea) block cipher. Technical report, National Institute of Standards and

Technology (2017). * Naresh, V., Sivaranjani, R. & Murthy, N. Provable secure lightweight multiple shared key agreement based on hyper elliptic curve diffie-hellman for wireless sensor

networks. _Int. J. Crit. Infrastruct. Prot._ 28, 100,371 (2020). Google Scholar  * Trzepieciński, T. & Lemu, H. G. Improving prediction of springback in sheet metal forming using

multilayer perceptron-based genetic algorithm. _Materials_ 13, 3129 (2020). Article  ADS  PubMed  PubMed Central  Google Scholar  * Maulud, D. & Abdulazeez, A. M. A review on linear

regression comprehensive in machine learning. _J. Appl. Sci. Technol. Trends_ 1, 140–147 (2020). Article  Google Scholar  * Wu, L. et al. A recurrent neural network-accelerated multi-scale

model for elasto-plastic heterogeneous materials subjected to random cyclic and non-proportional loading paths. _Comput. Methods Appl. Mech. Eng._ 369, 113,234 (2020). Article  MathSciNet 

Google Scholar  * Meng, H., Geng, M. & Han, T. Long short-term memory network with bayesian optimization for health prognostics of lithium-ion batteries based on partial incremental

capacity analysis. _Reliab. Eng. Syst. Saf._ 236, 109,288 (2023). Article  Google Scholar  * Blanchard, P., El Mhamdi, E.M., Guerraoui, R., Stainer, J., Machine learning with adversaries:

byzantine tolerant gradient descent. _In_: International Conference on Neural Information Processing Systems p. 118–128 (2017). * Karimireddy, S.P., He, L., Jaggi, M., Learning from history

for byzantine robust optimization. _In_: International Conference on Machine Learning, pp. 5311–5319 (2021). * Chen, Y., Su, L. & Xu, J. Distributed statistical machine learning in

adversarial settings: Byzantine gradient descent. _Proc. ACM Meas. Anal. Comput. Syst._ 1, 1–25 (2017). CAS  Google Scholar  * Yin, D., Chen, Y., Kannan, R., Bartlett, P., Byzantine-robust

distributed learning: towards optimal statistical rates. _In_: International Conference on Machine Learning, pp. 5650–5659 (2018). * Zhang, G. et al. Reaching consensus in the byzantine

empire: a comprehensive review of BFT consensus algorithms. _ACM Comput. Surv._ 56, 1–41 (2024). Article  Google Scholar  * Wang, R. et al. Matswarm: trusted swarm transfer learning driven

materials computation for secure big data sharing, https://zenodo.org/records/13622509 (2024). Download references ACKNOWLEDGEMENTS This work is supported in part by the National Key

Research and Development Program of China under Grant 2021YFB3702403, and in part by the National Natural Science Foundation of China under Grant 62101029. R.W. has been supported by the

China Scholarship Council Award under Grant 202306460078. C.X. has been supported in part by the China Scholarship Council Award under Grant 202006465043. AUTHOR INFORMATION AUTHORS AND

AFFILIATIONS * School of Computer and Communication Engineering, University of Science and Technology Beijing, 100083, Beijing, China Ran Wang, Cheng Xu, Fangwen Ye, Yusen Tang, Sisui Tang, 

Hangning Zhang, Wendi Du & Xiaotong Zhang * Beijing Advanced Innovation Center for Materials Genome Engineering, University of Science and Technology Beijing, 100083, Beijing, China Ran

Wang, Cheng Xu & Xiaotong Zhang * College of Computing and Data Science, Nanyang Technological University, 639798, Singapore, Singapore Ran Wang & Shuhao Zhang * Shunde Innovation

School, University of Science and Technology Beijing, 528399, Guangdong, China Cheng Xu & Xiaotong Zhang Authors * Ran Wang View author publications You can also search for this author

inPubMed Google Scholar * Cheng Xu View author publications You can also search for this author inPubMed Google Scholar * Shuhao Zhang View author publications You can also search for this

author inPubMed Google Scholar * Fangwen Ye View author publications You can also search for this author inPubMed Google Scholar * Yusen Tang View author publications You can also search for

this author inPubMed Google Scholar * Sisui Tang View author publications You can also search for this author inPubMed Google Scholar * Hangning Zhang View author publications You can also

search for this author inPubMed Google Scholar * Wendi Du View author publications You can also search for this author inPubMed Google Scholar * Xiaotong Zhang View author publications You

can also search for this author inPubMed Google Scholar CONTRIBUTIONS R.W. and C.X. conceived this project. C.X. and X.Z. funded and supervised the research. R.W. and F.Y. implemented the

algorithm, performed the experiments, and prepared the plots. Y.T., S.T., H.Z., and W.D. implemented the open-source prototype. R.W. and C.X. analyzed the results and drafted the main text.

C.X., S.Z. and X.Z. revised the manuscript. All authors commented on the manuscript. CORRESPONDING AUTHORS Correspondence to Cheng Xu or Xiaotong Zhang. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Ernestina Mensalvas and the other anonymous reviewer(s) for their

contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION PEER REVIEW FILE DESCRIPTION OF ADDITIONAL SUPPLEMENTARY FILES SUPPLEMENTARY MOVIE 1

SUPPLEMENTARY MOVIE 2 SUPPLEMENTARY MOVIE 3 REPORTING SUMMARY SOURCE DATA SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, R., Xu, C., Zhang, S. _et al._ MatSwarm: trusted swarm transfer learning

driven materials computation for secure big data sharing. _Nat Commun_ 15, 9290 (2024). https://doi.org/10.1038/s41467-024-53431-x Download citation * Received: 11 November 2023 * Accepted:

07 October 2024 * Published: 28 October 2024 * DOI: https://doi.org/10.1038/s41467-024-53431-x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative