Reader TTS

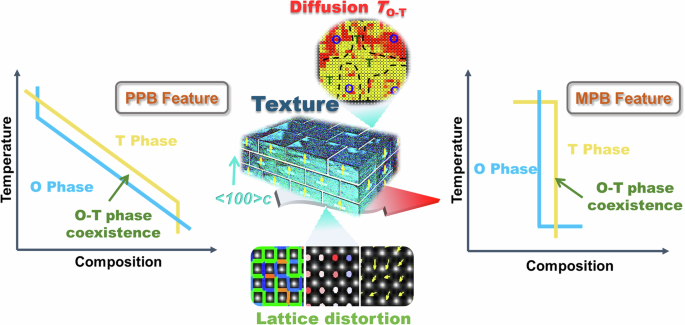
ABSTRACT The contradiction between high piezoelectricity and uniquely poor temperature stability generated by polymorphic phase boundary is a huge obstacle to high-performance (K, Na)NbO3

-based ceramics entering the application market as Pb-based substitutes. We possess the phase boundary by mimicking Pb(Zr, Ti)O3’s morphotropic phase boundary structure via the synergistic

optimization of diffusion phase boundary and crystal orientation in 0.94(Na0.56K0.44)NbO3−0.03Bi0.5Na0.5ZrO3−0.03(Bi0.5K0.5)HfO3 textured ceramics. As a result, a prominent comprehensive

performance is obtained, including giant _d_33 of 550 ± 30 pC/N and ultrahigh temperature stability (_d_33 change rate less than 1.2% within 25-150 °C), representing a significant

breakthrough in lead-free piezoceramics, even surpassing the Pb-based piezoelectric ceramics. Within the same temperature range, the _d_33 change rate of the commercial Pb(Zr, Ti)O3−5

ceramics is only about 10%, and more importantly, its _d_33 (~ 350 pC/N) is much lower than that of the (K, Na)NbO3-based ceramics in this work. This study demonstrates a strategy for

constructing the phase boundary with MPB feature, settling the problem of temperature instability in (K, Na)NbO3-based ceramics. SIMILAR CONTENT BEING VIEWED BY OTHERS ULTRAHIGH

PIEZOELECTRIC PERFORMANCES OF (K,NA)NBO3 BASED CERAMICS ENABLED BY STRUCTURAL FLEXIBILITY AND GRAIN ORIENTATION Article Open access 21 January 2025 ULTRAHIGH PIEZOELECTRICITY AND TEMPERATURE

STABILITY IN PIEZOCERAMICS BY SYNERGISTIC DESIGN Article Open access 11 February 2025 MULTISCALE RECONFIGURATION INDUCED HIGHLY SATURATED POLING IN LEAD-FREE PIEZOCERAMICS FOR GIANT ENERGY

CONVERSION Article Open access 22 March 2024 INTRODUCTION Piezoceramics can achieve the conversion of mechanical energy and electrical energy, endowing electromechanical devices with the

function of energy conversion. The salient permittivity and piezoelectric constant adjacent to the morphotropic phase boundary (MPB) determine that lead zirconate titanate (Pb(Zr, Ti)O3,

PZT)-based piezoceramics have dominated the piezoceramics market1,2. In response to the call for environmental protection and sustainable development, it is urgent to develop competitive

lead-free counterparts. Among several well-known lead-free piezoceramics, potassium sodium niobate (KNN) based ceramics with both high piezoelectric properties and Curie temperature have

sparked a research boom3,4,5,6. However, the comprehensive performance of pure KNN ceramic is far from comparable to lead-based piezoceramics, and tremendous efforts have been made to narrow

the gap between them7,8,9,10. Drawing on the experience of the MPB construction in lead-based ceramics, similarly, polymorphic phase boundary (PPB) was successfully constructed in KNN-based

ceramics to improve the piezoelectric performance11,12,13,14,15. To date, four main phase boundaries (Rhombohedral - Orthorhombic, Orthorhombic - Tetragonal, Rhombohedral - Tetragonal,

Rhombohedral - Orthorhombic - Tetragonal) have been obtained at room temperature in KNN-based piezoceramics. Researchers represented by Wu et al. have successfully surpassed the _d_33 of

KNN-based ceramics by 600 pC/N based on the PPB construction, greatly stimulating the enthusiasm of researchers16,17,18. However, it is worth noting that MPB in lead-based systems is

essentially a composition-driven phase boundary that is virtually independent of temperature, whereas PPB shows a clear temperature dependence. Thereby, by suffering from polycrystalline

phase boundaries, these state-of-the-art KNN-based ceramics exhibit severe temperature instability of the _d_3319. Generally, not only the high piezoelectric coefficient but also the

corresponding stability over temperature range of −20 to 140 °C are crucial for practical applications. How to simultaneously improve the piezoelectricity and its temperature stability in

one sample becomes a pivotal issue for KNN-based ceramics. Hence, the construction of traditional PPB, accompanied by abrupt phase transition, is far from meeting the requirements for

improving the comprehensive performance of KNN-based ceramics. In recent years, PPB with a relatively diffused phase transition at room temperature has been discovered. The presence of

diffused PPB alleviates the significant performance fluctuations near the phase transition. Therefore, researchers attempt to modulate PPB in KNN-based ceramics through various strategies,

transforming it from a temperature-sensitive traditional PPB to a temperature-insensitive diffused PPB20,21,22,23,24,25,26,27,28. For example, Li et al. utilized CaZrO3 doping to obtain

relatively diffused phase transition characteristics at room temperature, resulting in the strain varying less than 10% in the temperature regime from room temperature up to 175 °C27.

Through the multiphase coexistence strategy, Xi et al. also achieved the same trend of change in the piezoelectric constant (_d_33) and dielectric constant of KNN-based ceramics within

certain temperature range, breaking the bottleneck of its high temperature dependence29. Subsequently, researchers have found that constructing composition-driven successive and diffused

phase boundaries is also an efficient method to improve the temperature stability of the piezoelectric coefficient. For instance, Wu et al. pioneered the construction of diffused PPT by

designing compositionally graded composites, achieving an excellent _d_33 change rate of 6% within the temperature range of 25–100 °C and the _d_33 change rate of 25% in the range of 25–150 

°C. Although its piezoelectric coefficient was not satisfactory enough (~350 pC/N), this study laid an important foundation for improving the temperature stability of KNN-based

ceramics30,31. The discovery of PPB with diffused phase transition characteristics has brought dawn to KNN-based ceramics with high piezoelectric performance to achieve temperature

independence. However, there is still a certain discrepancy between diffused PPB and MPB, which urgently requires us to address this issue. Inspired by the above considerations, we urgently

need to develop a kind of KNN-based ceramics with excellent comprehensive performance to mitigate the inconsistency of high _d_33 and its temperature stability. In view of the great

advantages of texture technology in significantly increasing the _d_33 and the temperature independence of domains, we are eager to solve the above problems by adopting both strategies

simultaneously to mimic PZT’s MPB structure in KNN-based textured ceramics, albeit difficult to realize19,25,26,27,32,33,34,35,36. Hence, a new-type phase boundary with MPB feature was

constructed to solve this puzzle in this work, which is achieved by introducing (Bi0.5K0.5)HfO3 into the 0.97(Na0.56K0.44)NbO3−0.03Bi0.5Na0.5ZrO3 matrix and simultaneously introducing

texture technology, where Bi3+and Hf4+ contribute to the formation of O-T coexisting phase boundary29,34. It is expected that this kind of phase boundary with MPB feature will adjust the

stability of _d_33 over a wide temperature range, as the fluctuation of the piezoelectric coefficient _d_33 with temperature variation caused by the conventional abrupt polymorphic phase

transition will be preliminarily suppressed to some extent. Meanwhile, the <00_l_>C crystal orientation induced by texture technology and the construction of the O-T phase boundary can

also greatly promote the polarization switching of piezoelectric materials, significantly improving their piezoelectric performance. Therefore, we successfully obtained ultra-high

temperature stability of _d_33 (the change rate less than 1.2% within the temperature range of 25–150 °C and less than 10% within 25–250 °C) and piezoelectric coefficient (_d_33~550 ± 30 

pC/N) in the (0.97-_x_)(Na0.56K0.44)NbO3−0.03Bi0.5Na0.5ZrO3-_x_(Bi0.5K0.5)HfO3 (KNN-BNZ-_x_BKH) textured ceramics. This work provides a key approach for the development of practical

lead-free KNN-based piezoelectric ceramics (Fig. 1). RESULTS AND DISCUSSION FORMATION OF CRYSTAL ORIENTATION AND PHASE BOUNDARY WITH MPB FEATURE The SEM images of the KNN-BNZ-_x_BKH ceramics

are shown in Fig. S1. Notably, it can be seen that the textured ceramics (abbreviated as _x_T) exhibit typical brick-wall-like grains aligned parallel to the tape-casting plane, and the

grain size is significantly larger than that of random ceramics (abbreviated as _x_R). The large grains of the te_x_tured ceramics (~20–30 μm) are close to the size of NN templates (Fig. 

S2), indicating that the NN seed templates act as a nucleation site during grain growth. In addition, as a representative component of electrical properties, the energy-dispersive

spectroscopy (EDS) analysis also shows that the element distribution in 3T ceramics is uniform and there are no other impurity phases, as shown in Fig. S3. The X-ray diffraction (XRD)

patterns of KNN-BNZ-_x_BKH ceramics for both random and textured ceramics are shown in Figs. S4a and S5. All samples exhibit typical perovskite structure and the (00_l_) diffraction peaks of

the textured ceramics are significantly higher than those of the random ceramics, indicating strong crystal orientation along <00_l_>c. The Lotgering factor _f_(00_l_) can be used to

calculate the texturing degree of the sample, and the corresponding _f_(00_l_) was calculated to be 98.7%, 98.3%, 98.7%, and 85.8% for the textured ceramics with _x_ = 0.01 − 0.04,

respectively37. In addition, the electron backscattered diffraction (EBSD) pole diagram (Fig. 2e) and inverse pole diagram (Fig. 2f) of 3T ceramics were tested along the direction

perpendicular to the casting direction, indicating the high texture degree of the ceramics. The high orientation degree is attributed to the high-quality NaNbO3 templates and reasonably

designed sintering process. The phase structure with varied BKH concentration can be determined by combining the (002)/(200) characteristic diffraction peaks, _ε_r-_T_ curves, and Raman

spectrum. As shown in Fig. S4a, with the increase of _x_, the intensity of the (002) peak in _x_R ceramics is gradually exceeded by (200), and even almost disappears, indicating that a

continuous phase transition occurs, e.g., a gradual increase of the T phase and a gradual decrease of the O phase. In addition, as shown in Fig. S4b, with the increase of _x_, although the

O-T phase boundary cannot be clearly seen, it gradually shifted to low temperature, while the R-O phase boundary was significantly suppressed and disappeared at liquid nitrogen temperature.

Therefore, combining the analyses of both XRD patterns and _ε_r-_T_ curves, we can deduce that the 0R ceramics belong to the single orthogonal phase, while the _x_R ceramics with 0.01 ≤ _x_ 

≤ 0.04 can be determined as the coexistence of O and T phases. Due to the presence of _T_O-T at room temperature, the 3R ceramics have a comparable content of O and T phases, which greatly

reduces the Gibbs free energy and contributes to the improvement of ferro/piezoelectrical properties. On the contrary, due to the _T_O-T deviates from room temperature, 2R and 4R ceramics

have more O and T phases, respectively. Hence, the room temperature _ε_r of the _x_R ceramics first increases because it approached to the phase boundary (i.e., _x_ = 0 − 0.03), but then

decreases because of the reduced degree of phase boundary and the significantly destroyed long-range ordering at high contents of (Bi0.5K0.5)HfO3 (i.e., _x_ = 0.04)38. It is noteworthy that

the phase transition law of the _x_T ceramics is similar to that of the _x_R ceramics (Fig. S5), and the _T_O-T of 3T is also located at room temperature (Fig. 2c, Figs. S6 and S7). However,

the O-T phase boundary of _x_T ceramics almost disappears, in particular _x_ = 0.03, the phase structures exhibit similarities to the MPB structure in PZT (Fig. 2c). Thus, unlike other

KNN-based ceramics, the corresponding phase diagrams represented by _x_T ceramics can be drafted as shown in Fig. 2d. KNN-based ceramics with MPB feature will correspondingly exhibit

excellent temperature stability of ferro/piezoelectrical properties. To further illustrate the newly discovered phase boundary of _x_T ceramics, the in-situ variable temperature XRD patterns

are shown in Fig. 2a, b. From the measurements, not only the high Curie temperature of 3T ceramics can be observed (~330 °C), but the phase structure (coexistence of O and T phases) is also

stable from room temperature to ~200 °C, revealing the phase boundary in 3T ceramics are similar to MPB, which is consistent with the _ε_r-_T_ curves. In addition, we also conducted XRD

Rietveld refinement as shown in Fig. S8. The results indicate that there is a coexisting O-T phase structure in the temperature range of 25–200 °C, and the changes are very subtle with

increasing temperature. At 25 °C, 100 °C, and 200 °C, the proportion of O phase is 68.378%, 65.206%, and 62.093%, respectively. Finally, the phase structure transforms to a cubic phase and a

small amount of T phase at 350 °C. Overall, the multiphase coexistence phase boundary with MPB feature and high <00_l_> crystallographic orientation will play an important role in

obtaining excellent comprehensive piezoelectricity for the 3T ceramics. To further resolve the local structural information of the textured KNN-BNZ-BKH ceramics, aberration-corrected

atomic-resolution scanning transmission electron microscopy (STEM) was employed. Fig. 3e gives a STEM annular Bright-Field (ABF) image along the [100] zone axis. For ferroelectric KNN-based

materials, the polarization vectors are determined by the displacement from B-site cations (stronger intensity contrast, Nb) to the center of the four nearest neighboring A-site cations

(weaker intensity contrast, Na/K) based on 2D Gaussian peak fitting. It is clearly shown that the _δ_Nb−Na/K vectors are not homogeneous (as expected in normal ferroelectrics with a single

phase); instead, they are heterogeneous, i.e., mainly lying along the pseudocubic axes in the left part and along the diagonals in the right part, corresponding to the T and O symmetries,

respectively, as schematically shown in the inset of Fig. 3e. After peak finding with the method of 2D Gaussian peak fitting, with an accuracy ~5 pm, the _δ_Nb-O displacement vector map can

be obtained, as shown in Fig. 3f, g. Based on the schematic figure (the inset), T and O nanoregions can be identified, which is consistent with XRD analysis results. The dominance of

large-scale long-range ordered polarization regions consisting of O and T phases can be clearly observed by combining the arrows in the zone axis along [100] zone axis, while short-range

disordered multiphase nanoclusters occupy less, which is quite different from the local structure of KNN-based ceramics with R-O-T multiphase coexistence9,17. Fig. 3n is a statistical chart

of the polarization direction in quadrants. The results indicate that the O phase is the majority phase. Fig. 3f, g clearly shows the gradual polarization rotation between different states.

Such nanoscale balanced multiphase coexistence may possess almost isotropic free energy and thus significantly decreased polarization anisotropy. We also performed the calculation of the key

length of both A and B sites, as shown in Fig. 3h, o, the reddish lines indicate longer bond lengths, the bluish lines indicate shorter bond lengths, and the green lines represent the

average normal bond lengths. We utilized the Z-contrast feature of STEM to draw the A site intensity map, as shown in Fig. 3i, p, the reddish atoms represent heavier elements, while the

bluish atoms indicate lighter elements. Fig. 3k–m present the local images of the O phase, T phase, and the boundary of the O-T phase, respectively, extracted from Fig. 3h–j. It can be

observed that the O regions exhibit less heavy dopants (Bi) in A sites and weaker lattice distortion, compared with the T regions; while the O-T phase boundary regions show the most dopants

and strongest lattice distortion. The local segregation of doping elements leads to the formation of the phase coexistence of O and T nanophases. As shown in Fig. 3o, p, the bond lengths and

the atom intensities at B sites are relatively uniform, with fewer fluctuations, which is due to the relative differences in the atom size and atom number between B-site dopants (Zr and Hf)

and Nb matrix are relatively small, compared with the A-site dopants Bi and K/Na matrix (Tables S1 and S2). The results provide insights into the relationship between A/B-site doping and

the formation of the O-T phase boundary, guiding the doping behavior of KNN-based piezoelectric ceramics. FERROELECTRICITY AND PIEZOELECTRICITY Fig. S9a demonstrates the _P-E_ hysteresis

loops of the _x_T ceramics tested at 30 kV/cm and 10 Hz. Although the coercive field (Ec) of _x_T ceramics is comparable to that of _x_R ceramics, all the _x_T ceramics exhibit more

well-saturated square _P-E_ hysteresis loops with relatively larger remnant polarization (Pr) and maximum polarization (Pmax) than _x_R ceramics (Fig. S9b), such as, the Pr is close to 28

μC/cm2 in 3T ceramics, while in 3R ceramics, the Pr is only around 21 μC/cm2, indicating enhanced ferroelectricity. The crystal orientation makes the arrangement of dipoles more effective

under the applied electric field, thereby improving the polarization efficiency and ferroelectricity of _x_T ceramics. The ferroelectricity is also influenced by the phase structure. It can

be seen that the changes in Pr and Pmax of the KNN-BNZ-_x_BKH ceramics regardless of texture and random keep increasing from _x_ = 0.01 to 0.03 as the O-T phase boundary gradually moved

towards room temperature, and then decrease at _x_ = 0.04. Meanwhile, Ec also gradually decreases with the increase of the T phase, consistent with previously reported results39. This is

initially associated with a decrease in free energy due to the emergence of the phase boundary, followed by an increase in relaxor feature due to the gradual dominance of the T phase.

Compared with their random counterparts, the textured ceramics achieved significant improvements in both strain and piezoelectricity, especially for the 3T ceramics, which not only possessed

both high piezoelectric coefficient and high Curie temperature (_d_33~550 pC/N, _T_C~330 °C, Fig. S10b), but also observed a large strain of ~0.2% at 30 kV/cm (Fig. S10a). Such excellent

comprehensive performance is highly competitive in lead-free piezoceramics (Fig. S11)3,5,9,25,27,34,35,40,41,42,43,44,45,46,47. It should be noted that the random and textured KNN-BNZ-_x_BKH

ceramics share a similar chemical composition and room temperature phase structure, and the significant difference in piezoelectricity between them mainly stems from the high crystal

orientation. Therefore, the superposition of the effective arrangement of dipoles caused by the preferred crystal orientation and the low domain wall energy of the phase boundary contributes

to the easy polarization rotation along different polarization states under an external electric field, thus obtaining a high piezoelectric response. To further establish the relationship

between performance and microstructure, the 3T ceramics were subjected to in-situ electric field X-ray diffraction tests, and the corresponding (200)/(002) peaks are shown in Fig. 2g and

Fig. S12. As the applied electric field increases, the position of (002)/(200) peaks slightly moved to the lower 2_θ_ due to the lattice distortion caused by electric field. More

importantly, it is also observed that the peak intensity ratios of the (002)/(200) change gradually with the increase of the applied electric field, resulting in a continuous phase

transition from the O-T phase to the pure O phase, in particular near the coercive field (~14 kV/cm). Fig. 2h shows the crystal structure evolution of the T-O sequential phase transition.

The above results provide key evidence to reveal that efficient polarization rotation occurs inside the 3T ceramics under the action of an external electric field18. It is noteworthy that

the phase transition is almost irreversible after the withdrawal of the electric field, indicating a high irreversible lattice distortion, leading to high residual polarization and excellent

piezoelectricity. The structure of domains is closely related to the electrical properties of ferroelectric materials48,49,50, and the SEM images of acid-etched domain patterns are shown in

Fig. 3a, b. Not only the morphology of the watermark domain, the T/O phase-related abundant hierarchical domain structure inside can be seen visually. The hierarchical domain architecture

originates from low domain wall energy and almost disappeared polarization anisotropy, typically occurring in multiphase coexisting regions, which not only facilitates the reduction of the

coercive field but also plays an important role in the construction of diffusion-type phase boundary29. In addition, it can be seen from the complete SEM images that there is a significant

difference in the grain size between 3R ceramics and 3T ceramics, as shown in Fig. S13. Due to the large grain size, the overall domain size in 3T ceramics is significantly larger than that

in 3R ceramics, which can be further verified in TEM images (Fig. 3c, d, and Fig. S14). The reduced coercive field caused by fewer grain boundaries and the preferred crystal orientation

compensates for the increased domain wall energy of the larger domains, resulting in comparable Ec in _x_T and _x_R ceramics (Fig. S9a, b), which allows the larger-sized domains in 3T

ceramics to undergo efficient switching and contributes to a more saturated polarization. Therefore, the high piezoelectric response of 3T ceramics also benefits from the contribution of

larger-size domains. In addition, from the element mapping images of TEM, it can be further clearly seen that the several main elements in 3T ceramics are uniformly distributed without

obvious impurities (Fig. S15). PIEZOELECTRIC TEMPERATURE STABILITY The heat generated by piezoelectric materials during service or fluctuations in external temperature can cause changes in

the temperature of the material itself. Therefore, in addition to focusing on the performance of piezoelectric materials at room temperature, the temperature stability of piezoelectric

performance is also a very important indicator for transducer and sensor applications, especially the small signal piezoelectric coefficient _d_33 (i.e., direct piezoelectric

effect)51,52,53,54. It is well known that _d_33 is proportional to _ε_r·Pr, so the temperature stability of both dielectric constant and ferroelectricity are closely related to the

piezoelectric temperature insensitivity. As shown in the _ε_r-_T_ curves (Fig. 2c), it can be seen that the O-T phases boundary with MPB feature makes the _ε_r of 3T ceramics rise slowly

between room temperature and Curie temperature, and remains almost at a horizontal line until 150 °C. In contrast, from the in-situ variable temperature _P-E_ hysteresis loops (Fig. S16), it

can be found that both the Pmax and Pr decrease slowly from room temperature to 180 °C. Thus, the complementary effect between the dielectric constant and Pr may lead to the temperature

stability of the piezoelectricity for the 3T ceramics. The stability of piezoelectric performance is also closely related to the internal structure of ceramics, so we conducted a detailed

analysis of the poled phase structure and domain structure. Fig. 4a shows the in-situ temperature-dependent XRD of 3T ceramics after poled. As the temperature increases, the XRD diffraction

peaks remain basically unchanged below 200 °C. Peak fitting was performed on the (002)/(200) peaks (Fig. S17) in order to more accurately understand the changes in phase composition. As can

be seen in Fig. S17b, only the single O phase exists in the range from room temperature to 150 °C, and the T phase begins to gradually emerge only when the temperature approaches 200 °C,

exhibiting excellent temperature stability of the phase structure similar to that of the pre-poled one, which greatly improves the temperature stability of Pr and the post-poled _ε_r.

Moreover, we also investigated the evolution of poled domain structure through in-situ variable temperature PFM and TEM measurements. It can be seen that after poled, the micron-scale

macrodomains of the 3T ceramics (Fig. S18d) undergo efficient switching and domain growth, resulting in the phase of all domains becoming almost 180° (Fig. S18a), consistent with the high

Pr. Macroscopically, no significant large-scale poled domain recovery occurred when the temperature increases to 200 °C (Fig. S18a–c), which is another key factor for Pr to maintain good

temperature stability. While locally, due to thermally stimulated degradation of some unstable smaller domain structures, the peak intensity of the ±180° domains gradually weakened with

increasing temperature (inset of Fig. S18a–c). The in-situ variable temperature TEM was further used to investigate the evolution of poled large-sized stripe domains with temperature in 3T

ceramics, as shown in Fig. 4b. It can be clearly observed that the large-sized stripe domains can be well maintained at 280 °C. The number of domains has not decreased, and their morphology

remains intact. When approaching the _T_C, the corresponding domain structure begins to be destroyed and disappears, resulting in depolarization. In addition to stable phase structure, the

large-sized domain structure plays an important role in resisting thermal depoled, as the disturbance of larger domain requires a higher driving force. To investigate the temperature

response of internal structure for textured ceramics and random multiphase ceramics with different domain sizes after poled, phase-field simulation was employed. Several effects were

considered in our model: Firstly, the ferroelectric polycrystal structures with different grain sizes (KNN system) were generated, resulting in textured or random orientations at different

grains. Secondly, the random fields were employed due to the presence of defects caused by doping. After the domain structure evolution is stable, a polarization electric field of up to 3 

kV/mm was applied to observe the changes in domain structure with temperature. Fig. 4c1–c4 and d show the simulated domain structure changes of the large macrodomains for the textured

multiphase ceramics and the small macrodomains for the random multiphase ceramics after poled and the corresponding temperature response. The textured ceramics with larger domain structures

exhibit a more saturated polarization state after poled, which is beneficial for piezoelectricity. More importantly, its poled domain structure can remain stable at higher temperatures

without being damaged (e.g., >173 °C), which is consistent with actual experimental results. Furthermore, we also found through EPR tests that in addition to more oxygen vacancy defects

introduced by the increase in _x_BKH, the oxygen vacancy content of _x_T ceramics was also higher than that of _x_R ceramics (Fig. S19). The generation of oxygen vacancies tends to form

defect dipoles in ferroelectric ceramics and will be aligned along the applied electric field, which has a pinning effect on the poled domain structure and increases the depolarization

energy, thus improving the domain stability31, as shown in Fig. 4c5–c8. Therefore, comprehensive structural analysis and simulations have ascertained that in addition to the stable phase

structure induced by the multiphase coexistence phase boundary with the MPB feature, the larger domain size and the pinning of defects are closely related to the temperature stability of the

domain structure. The stability of phase and domain structures will be beneficial for the piezoelectric temperature stability. Fig. 5a presents the in-situ temperature-dependent _d_33 of

the _x_T ceramics (_x_ = 0.01 − 0.04). Typically, when a PPT-type O-T phase boundary exists above room temperature, the _d_33 of KNN-based ceramics will shake up at _T_O-T and then drop with

increasing temperature, showing extreme sensitivity to temperature35. Whereas, in _x_T ceramics, the temperature sensitivity of the piezoelectric coefficient _d_33 decreases as the

diffusion of the O-T phase boundary increases with composition. For example, when 0.01 ≤ _x_ ≤ 0.02, the O-T phase boundaries are already very diffuse, effectively improving the temperature

stability, which can be confirmed by the in-situ temperature-dependent _d_33 value of _x_R and _x_T in Fig. 5a, b. When the _T_O-T is further shifted to room temperature or even below room

temperature, the phase boundary characteristics are even close to the MPB structure. Thus, for 3T ceramics, its high _d_33 remains almost unchanged (fluctuating by only 1.2%) from room

temperature to 150 °C. Even in the range of 25–250 °C, its _d_33 decreases by only 10%, and significant changes occur only when _T_C is reached. In random-oriented ceramics, the

corresponding components ceramics are of poor temperature stability due to insufficient diffusion, as shown in Fig. 5b. Therefore, the new phase boundary with MPB feature obtains an

unprecedented break through in temperature stability for high piezoelectric coefficient KNN-based ceramics (e.g., _d_33 > 400 pC/N) and also highly competitive concerning other studied

Pb/Pb-free ceramics (Fig. 5c–e)25,27,31,55,56,57,58. The collaborative optimization of crystal orientation and design of new phase boundary involved in this work provides an important

advance for optimizing the comprehensive piezoelectricity of KNN-based ceramics, especially temperature stability. In summary, ultra-high temperature stability and piezoelectric coefficient

were achieved in the 3T ceramics. Both the T/O phase local distortion associated with the O-T phase boundary in the atomic scale and the correlation between A/B-site doping and the formation

of the O-T phase boundary can be confirmed by STEM. While XRD as well as EBSD can further resolve the macro-scale crystal orientation. Benefiting from the O-T multiphase coexistence at room

temperature and high orientation, the material undergoes irreversible electric field-induced efficient large-size macro-domain switching and phase transitions, which exhibit high residual

polarization as well as a significantly improved _d_33. In addition, the synergistic effect between the ultra-high stability of phase structures and domain structures through mimicking PZT’s

MPB structure is the reason why the 3T ceramics break through the inherent drawbacks of temperature instability. The intrinsic reason is related to the induction of larger-size hierarchical

domain structure and the formation of point defect during the grain template growth method (TGG), which greatly improves the depolarization energy of the KNN-BNZ-_x_BKH textured ceramics.

Finally, the excellent thermal stability, with a change rate of less than 1.2% in the temperature range of 25–150 °C and less than 10% in the temperature range of 25–250 °C, coupled with

high piezoelectric coefficient (_d_33)~550 pC/N and high Curie temperature (_T_C)~330 °C, making the 3T ceramics a promising candidate for future lead-free piezoelectric ceramics

applications. METHODS SAMPLE PREPARATION The (0.97-_x_)(Na0.56K0.44)NbO3−0.03Bi0.5Na0.5ZrO3-_x_(Bi0.5K0.5)HfO3 (KNN-BNZ-_x_BKH) (0.01 ≤ _x_ ≤ 0.04) lead-free random and textured

piezoceramics were designed and prepared using conventional solid-state method and template grain growth (TGG) method, respectively. All raw materials, including Na2CO3 (Aladdin, 99.8%),

K2CO3 (Aladdin, 99.99%), Nb2O5 (Aladdin, 99.98%), Bi2O3 (Alpha, 99.98%), ZrO2 (Aladdin, 99.99%) and HfO2 (Alpha, 99.99%) were ball milled with ethyl alcohol and ZrO2 balls after weighting

according to the formula. The milled powders were calcined at 840–850 °C for 5 h after the ethyl alcohol dried off, then ball milled again for 12 h and dried. RANDOM PIEZOCERAMICS The

KNN-BNZ-_x_BKH matrix powders pressed into disks of 12-mm diameter and 1-mm thickness under the pressure of 200–300 MPa with a binder of 6 wt% polyvinyl alcohol. Subsequently, the pellets

were heated to 600 °C at 1 °C/min to burn out the binder and then sintered at the target temperature by two-step sintering, which was heated to 1150–1170 °C and then rapidly cooled to

1050–1070 °C for 10 h. In addition, the traditional one-step sintering involved in this work was to heat to the target temperature at a speed of 3 °C/min, and then conduct heat preservation

and furnace cooling. TEXTURED PIEZOCERAMICS To prepare tape-casting slurries, the KNN-BNZ-_x_BKH matrix powders, 4 mol % NaNbO3 templates, and organic binders were mixed in a solvent (50 wt%

alcohol and 50 wt% toluene). Then, the slurries with good liquidity were casted and form green tapes. The dried tapes were stacked and then pressed to form dense green bodies, which were

pressed into disks of 12 mm × 12 mm and 1 mm thickness under the pressure of 200–300 MPa. Subsequently, the pellets were heated to 600 °C at 1 °C/min to burn out the binder and then sintered

at the target temperature by two-step sintering, which was heated to 1180–1220 °C and then rapidly cooled to 1080–1120 °C for 10 h. CHARACTERIZATION OF ELECTRICAL PROPERTIES Via

mechanically thinning to 0.5 mm thickness, _x_T, and _x_R ceramics were coated by Ag electrodes on both sides for dielectric, ferroelectric, and electric field-induced strain tests.

Polarization (_P-E_) and strain (_S-E_) hysteresis loops were measured using a ferroelectric test system (Precision Premier II) at 10 Hz. The temperature-dependent polarization (_P-E_) loops

were achieved by the ferroelectric test system (Precision Premier II) with a heating stage. After poled at 30 kV cm−1 by AC electric field at room temperature, the piezoelectric coefficient

(_d_33) was tested at room temperature using a quasi-static _d_33 meter (ZJ-6A, Institute of Acoustics, China). The temperature-dependent piezoelectric coefficient (_d_33) was tested by a

quasi-static _d_33 meter (YE2730A, Sinocera, China), which was connected to a heating furnace. The temperature-dependent dielectric constants (_ε_r-_T_) curves were achieved by the Agilent

E4980A LCR meter and the Keithley 2410 Source Meter equipped with a heating stage (−110 to 400 °C). STRUCTURAL CHARACTERIZATION The surface and cross-section microstructure of the ceramics

were investigated with a scanning electron microscope (SEM, HITACHI, TM4000Plus). Electron backscatter diffraction (EBSD) pole figure and inverse pole figure for texture degree analyses and

energy-dispersive X-ray spectroscopy (EDS) were obtained by a field emission scanning electron microscope (FEI Magellan 400). The room temperature phase structure of the ceramics was tested

using an X-ray diffractometer (XRD, Bruker D2 PHASER). The specimens for transmission electron microscopy (TEM) were prepared by mechanical thinning, ultrasonic cutting, and Ar-ion thinning

until electrons can penetrate the samples with a thickness of ~30–50 nm. A JEOL JEM-2100F microscope was used to acquire the bright-field images for domain morphology. Oxygen vacancy defects

were proved by EPR (Bruker A300). Acid-etched domain structures were observed on a scanning electron microscopy (SEM) JSM-7610F. Before acid-etching, preparatory work such as lapping and

polishing was performed at room temperature. A mixed aqueous solution of HCl acid (with the mass concentration of about 37%, Laiyang Kangde Chem. Co., Ltd.) and HF acid (with a mass

concentration ≥40%, Tianjin Kemiou Chemical Reagent Co., Ltd.) in a volume ratio of 1:1 was used the etchant. The specimens for transmission electron microscopy (TEM) and atomic-resolution

scanning transmission electron microscopy (STEM) were prepared by mechanical thinning, ultrasonic cutting, and Ar-ion thinning until electrons can penetrate the samples with a thickness of

~30–50 nm. To reduce the impact of temperature on the poled sample, not only the required hot melt adhesive operation temperature for mechanical thinning is controlled at around 100 °C or as

low as possible, but also liquid nitrogen is assisted in the Ar-ion thinning process. A JEOL JEM-2100F microscope was used to acquire the bright-field images for domain morphology. The

atomic-scale imaging was carried out on a Cs-corrected Hitachi HF5000 microscope with ultra-high resolution (UHR) mode and a convergence/collection semi-angle of 20 mrad/60–320 mrad. IN-SITU

STRUCTURAL CHARACTERIZATION In-situ XRD under different temperatures was collected using X-ray diffractometer (PANalytical Empyrean, Holland). One self-made in-situ electric field XRD

sample holder was used to test the phase structure at different applied voltages (0–1000 V, sample thickness ~0.3 mm). The translucent gold electrodes by DC sputtering are used as electrodes

for testing the in-situ variable electric field XRD. In-situ Raman spectra were obtained at different temperatures using a Horiba Lab-Ram HR800 spectrometer with a laser wavelength of 532 

nm accompanied by an additional temperature probing stage. In-situ optimized vertical piezoresponse force microscopy (OV-PFM) images under different temperatures were obtained by

piezoresponse force microscope with additional temperature probing stage (PFM, Dimension Icon, Bruker, United States). The temperature-induced domain evolution was observed by a transmission

electron microscope (TEM, JEM 2100 F) equipped with a heating stage. PHASE-FIELD MODEL To describe the domain structures in textured and random grain structures, an order parameter \(\eta\)

was employed to represent the different crystal orientations. To separate the different grain orientations, two sets of coordinate system was used. The domain structures within each grain

can be described as local spontaneous polarization \({{{\bf{P}}}}_{L}\). In the global coordinate system, a global polarization P and a displacement field U were adopted as the order

parameters in the phase-field model. The temporal evolution of the polarization is described by the time-dependent Ginzburg-Landau (TDGL) equation and the stress/electric field equilibrium

equation59, $$\frac{{\partial {{\bf{P}}}}_{i}}{\partial t}=-L\frac{{\delta }F}{{{\delta }{{\bf{P}}}}_{i}}+{{{\bf{E}}}}_{i}^{{thermal}}$$ (1) $$\frac{\partial }{{\partial x}_{j}}({{\sigma

}}_{{ij}}(r,t))=0$$ (2) $${{\rm{\nabla }}}{{\rm{\cdot }}}{{\bf{D}}}={\rho }_{f}$$ (3) Here, _L_ is a kinetic coefficient related to domain wall mobility, _F_ is the total free energy of the

system, \(\frac{\delta F}{\delta {{{\bf{P}}}}_{i}}\) is the thermodynamic driving force, _σ__ij_ is the stress tensor, D is the electric displacement, \({\rho }_{f}\) is the free charge

density, _r,_ and _t_ are the spatial coordinate and time, respectively. The total free energy of a bulk system can be defined as follows, $$F

={F}_{{Land}}({{\bf{P}}})+{F}_{{grad}}({{\bf{P}}})+{F}_{{elastic}}({{\bf{P}}})+{F}_{{elec}}({{\bf{P}}},{{\bf{E}}}) \\ ={\int

}_{V}({f}_{{Land}}+{f}_{{grad}}+{f}_{{elastic}}+{f}_{{elec}}){dV}$$ (4) Where _F_ includes the bulk free energy \({F}_{{bulk}}({{\bf{P}}})\), domain wall energy \({F}_{{grad}}({{\bf{P}}})\),

elastic energy \({F}_{{elastic}}({{\bf{P}}})\), and electrostatic energy \({F}_{{elec}}({{\bf{P}}},{{\bf{E}}})\), E is the applied static electric field. _f_Land, _f_grad, _f_elastic and

_f_elec are the corresponding energy density. The bulk free energy density in a given grain can be expanded in terms of polarization components. For the KNN system, the bulk free energy

density can be described as: $${f}_{{Land}}=

{a}_{1}\left({{\bf{P}}}_{L1}^{2}+{{\bf{P}}}_{L2}^{2}+{{\bf{P}}}_{L3}^{2}\right)+{a}_{11}\left({{\bf{P}}}_{L1}^{4}+{{\bf{P}}}_{L2}^{4}+{{\bf{P}}}_{L3}^{4}\right) \\

+{a}_{12}\left({{\bf{P}}}_{L1}^{2}{{\bf{P}}}_{L2}^{2}+{{\bf{P}}}_{L1}^{2}{{\bf{P}}}_{L3}^{2}+{{\bf{P}}}_{L2}^{2}{{\bf{P}}}_{L3}^{2}\right)+{a}_{11}\left({{\bf{P}}}_{L1}^{6}+{{\bf{P}}}_{L2}^{6}+{\,{\bf{P}}}_{L3}^{6}\right)

\\

+{a}_{112}\left[{{\bf{P}}}_{L1}^{4}\left({{\bf{P}}}_{L2}^{2}+{{\bf{P}}}_{L3}^{2}\right)\,+\,{{\bf{P}}}_{L3}^{4}\left({{\bf{P}}}_{L2\,}^{2}+{{\bf{P}}}_{L1}^{2}\right)+{\text{P}}_{L2}^{4}\left({{\bf{P}}}_{L3}^{2}+{{\bf{P}}}_{L1}^{2}\right)\right]

\\ +{a}_{123}{{\bf{P}}}_{L1}^{2}{{\bf{P}}}_{L2}^{2}{{\bf{P}}}_{L3}^{2}+{a}_{1111}\left({{\bf{P}}}_{L1}^{8}+{{\bf{P}}}_{L2}^{8}+{{\bf{P}}}_{L3}^{8}\right) \\ +

{a}_{1112}\left[{{\bf{P}}}_{L1}^{6}\left({{\bf{P}}}_{L2}^{2}+{{\bf{P}}}_{L3}^{2}\right)+{{\bf{P}}}_{L3}^{6}\left({{\bf{P}}}_{L2}^{2}+{{\bf{P}}}_{L1}^{2}\right)+{{\bf{P}}}_{L2}^{6}\left({{\bf{P}}}_{L3}^{2}\,+{\,\text{P}}_{L1}^{2}\right)\right]\,

\\ +

{a}_{1122}\left({{\bf{P}}}_{L1}^{4}{{\bf{P}}}_{L2}^{4}+{{\bf{P}}}_{L1}^{4}{{\bf{P}}}_{L3}^{4}+{{\bf{P}}}_{L2}^{4}{{\bf{P}}}_{L3}^{4}\right)\,+{a}_{1123}({{\bf{P}}}_{L1}^{4}{{\bf{P}}}_{L2}^{2}{{\bf{P}}}_{L3}^{2}+{{\bf{P}}}_{L1}^{2}{{\bf{P}}}_{L2}^{4}{{\bf{P}}}_{L3}^{2}

\\ + {{\bf{P}}}_{L1}^{2}{{\bf{P}}}_{L2}^{2}{\text{P}}_{L3}^{4})$$ (5) where G is the Gibbs free energy of a cubic ferroelectric system, \({a}_{1}-{a}_{1123}\) is the Landau coefficient and

P_L_ is the polarization field in the local crystallographic coordinate system within each grain. A standard global coordinate system for all grains was introduced to solve the polycrystal’s

elasticity and electrostatic equilibrium equation. Three Euler angles were used to describe the orientation of different grains in the polycrystalline structure. Thus, the transformation

matrix from the global to local coordinate system is given by: $${tr}=\left\{\begin{array}{c}\cos {\varphi }\cos {\psi }-\cos {\theta }\sin {\varphi } \sin {\psi } \sin {\varphi }\cos {\psi

}+\cos {\theta }\cos {\varphi }\sin {\psi } \sin {\theta }\sin {\psi }\\ -\cos {\theta }\cos {\psi }\sin {\varphi }-\cos {\varphi }\sin {\psi } \hfill \cos {\theta }\cos {\varphi }\cos {\psi

} \; \mbox{-} \; \sin {\varphi }\sin {\psi } \sin {\theta }\cos {\psi }\\ \sin {\theta }\sin {\varphi }\hfill \mbox{-}\cos {\varphi }\sin {\theta }\cos {\theta }\end{array}\right\}$$ (6)

The polarization in the local coordinate system can be described as a transformation from the polarization in the global coordinate system through

$${{{\bf{P}}}}_{{Li}}=\frac{1}{2}{{{tr}}_{{ij}}{{\bf{P}}}}_{j}$$ (7) The gradient energy density in an anisotropic system can be calculated by

$${f}_{{grad}}=\frac{1}{2}{{g}_{{ijkl}}{{\bf{P}}}}_{i,j}{{{\bf{P}}}}_{k,l}$$ (8) where _g_ijkl is the gradient energy coefficient and \({{{\bf{P}}}}_{i,j}=\frac{\partial

{{{\bf{P}}}}_{i}}{\partial {x}_{j}}\). The elastic energy density can be described as: $${f}_{{elas}}=\frac{1}{2}{c}_{{ijkl}}{e}_{{ij}}{e}_{{kl}}=\frac{1}{2}{c}_{{ijkl}}({\varepsilon

}_{{ij}}-{\varepsilon }_{{ij}}^{0})({\varepsilon }_{{kl}}-{\varepsilon }_{{kl}}^{0})$$ (9) where \({c}_{{ijkl}}\) is the stiffness tensor, \({e }_{ij}\) is the elastic strain tensor,

\({\varepsilon }_{ij}\) is the total strain tensor, and is the eigenstrain, $${\varepsilon }_{{ij}}^{0}={\varepsilon }_{{Lij}}^{0}={Q}_{{ijkl}}{{{\bf{P}}}}_{{Lk}}{{{\bf{P}}}}_{{Ll}}$$ (10)

Where \({\varepsilon }_{{Lij}}^{0}\) is the eigenstrain with respect to the local coordinate system, \({Q }_{ijkl}\) is the electrostrictive coefficient tensor. Therefore, the eigenstrain in

the global coordinate system can be obtained from $${\varepsilon }_{{ij}}^{0}={{tr}}_{{ki}}{{tr}}_{{lj}}{\varepsilon }_{{Lkl}}^{0}$$ (11) The electrostatic energy density _f_elec of the

system in phase-field simulation is given by, $${f}_{{elec}}=-{{{\bf{P}}}}_{i}(r)({{{\bf{E}}}}_{i}(r)+{{{\bf{E}}}}_{{RF}})-{\frac{1}{2}{{\bf{P}}}}_{i}(r){{{\bf{E}}}}_{i}^{{in}}(r)$$ (12)

where \({{{\bf{E}}}}_{i}^{{in}}(r)\) is the E-field induced by the dipole moments, E_i_(_r_) is the applied electric field and E_RF_ is the local electric field caused by the random point

defects. The parameters60 (all in SI units) in details are \({a}_{1}=4.29 ({Coth}\left[\frac{140}{T}\right]-{Coth}\left[\frac{140}{657}\right]){\rm{\times }}1{0}^{7}\),

\(\,{a}_{11}\text{=-}2.73 \times 1{0}^{8}\), \({a}_{12}\text{=}1.0861{\rm{\times }}1{0}^{9}\), \({a}_{111}\text{=}3.04{\rm{\times }}1{0}^{9}\), \({a}_{112}\text{=-}2.73{\rm{\times

}}1{0}^{9}\), \({a}_{123}\text{=}1.55{\rm{\times }}1{0}^{10}\), \({a}_{1111}\text{=}2.4{\rm{\times }}1{0}^{10}\), \({a}_{1112}\text{=}3.73{\rm{\times

}}1{0}^{9}\),\(\,{a}_{1122}\text{=}3.34{\rm{\times }}1{0}^{10}\), \({a}_{123}=\text{-}6.2{\rm{\times }}1{0}^{10}\), \({Q}_{11}\text{=}0.13\), \({Q}_{12}\text{=-}0.047\),

\({Q}_{44}\text{=}0.052\), \({{s}}_{11}\text{=}5.5{\rm{\times }}1{0}^{-11}\), \({s}_{12}\text{=-}1.6{\rm{\times }}1{0}^{-10}\), \({s}_{44}\text{=}1.3{\rm{\times }}1{0}^{-9}\). Where _s_ is

the Compliance coefficients and _Q_ is the electrostrictive coefficients. _A_ random electric field that obeys the Gaussian distribution \(N(0,\,\triangle )\) was applied, where \(\triangle

\) is the variance of the Gaussian distribution and can be connected with doping concentration. The simulation scale is 256 _dx_ × 256 _dz_. The grid scales _d_x and _d_z are 1 μm. 9

different grain orientations with the rotations about z direction from −20 to 20 degrees were used to account for the random grain structures. The Fourier method was used for solving the

equations. The open circuit electrical boundary condition and the periodic mechanical boundary conditions are adopted in the calculations. REPORTING SUMMARY Further information on research

design is available in the Nature Portfolio Reporting Summary linked to this article. DATA AVAILABILITY The authors declare that the main data supporting the findings of this study are

available within the article and its Supplementary Information files. Extra data are available from the corresponding author upon request. Source data are provided with this paper.

REFERENCES * Perdew, J. P. et al. Generalized gradient approximation made simple. _Phys. Rev. Lett._ 77, 3865–3868 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Waqar, M. et al.

Evolution from lead-based to lead-free piezoelectrics: engineering of lattices, domains, boundaries, and defects leading to giant response. _Adv. Mater._ 34, 2106845 (2022). Article  CAS 

Google Scholar  * Kroutvar, M. et al. Optically programmable electron spin memory using semiconductor quantum dots. _Nature_ 432, 81–84 (2004). Article  ADS  CAS  PubMed  Google Scholar  *

Liu, H. J. et al. Giant piezoelectricity in oxide thin films with nanopillar structure. _Science_ 369, 292 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Wu, J. et al. Potassium-sodium

niobate lead-free piezoelectric materials: past, present, and future of phase boundaries. _Chem. Rev._ 115, 2559–2595 (2015). Article  CAS  PubMed  Google Scholar  * Lee, M. H. et al.

High-performance lead-free piezoceramics with high curie temperatures. _Adv. Mater._ 27, 6976 (2015). Article  CAS  PubMed  Google Scholar  * Wang, X. P. et al. Giant piezoelectricity in

potassium-sodium niobate lead-free ceramics. _J. Am. Chem. Soc._ 136, 2905–2910 (2014). Article  CAS  PubMed  Google Scholar  * Ahart, M. et al. Origin of morphotropic phase boundaries in

ferroelectrics. _Nature_ 451, 545 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Lv, X. et al. Emerging new phase boundary in potassium sodium-niobate based ceramics. _Chem. Soc. Rev._

49, 671 (2020). Article  CAS  PubMed  Google Scholar  * Lin, J. F. et al. Field-induced multiscale polarization configuration transitions of mesentropic lead-free piezoceramics achieving

giant energy harvesting performance. _Adv. Funct. Mater._ 33, 2303965 (2023). Article  CAS  Google Scholar  * Pan, D. et al. Phase structure, microstructure, and piezoelectric properties of

potassium-sodium niobate-based lead-free ceramics modified by Ca. _J. Alloys Compd._ 693, 950 (2017). Article  CAS  Google Scholar  * Li, F. et al. Investigation of new lead free (1-x)

KNNS-(x)BKZH piezo-ceramics with R-O-T phase boundary. _J. Mater. Sci. Mater. Electron._ 28, 880 (2017). Google Scholar  * Deng, Y. et al. Structural and electric properties of MnO2-doped

KNN-LT lead-free piezoelectric ceramics. _Crystals_ 10, 1 (2020). Article  Google Scholar  * Zhang, Y. et al. Effect of three step sintering on piezoelectric properties of KNN-based lead

free ceramics. _Chem. Phys. Lett._ 758, 137906 (2020). Article  CAS  Google Scholar  * Qiao, L. et al. Full characterization for material constants of a promising KNN-based lead-free

piezoelectric ceramic. _Ceram. Int._ 46, 5641–5644 (2020). Article  CAS  Google Scholar  * Xu, K. et al. Superior piezoelectric properties in potassium-sodium niobate lead-free ceramics.

_Adv. Mater._ 28, 8519–8523 (2016). Article  CAS  PubMed  Google Scholar  * Zheng, T. et al. High-performance potassium sodium niobate piezoceramics for ultrasonic transducer. _Nano Energy_

70, 104559 (2020). Article  CAS  Google Scholar  * Zheng, T. et al. The structural origin of enhanced piezoelectric performance and stability in lead free ceramics. _Energy Environ. Sci._

10, 528–537 (2017). Article  CAS  Google Scholar  * Gao, J. H. et al. Large piezoelectricity in Pb-free 0.96(K0.5Na0.5)0.95Li0.05Nb0.93Sb0.07O3−0.04BaZrO3 ceramic: a perspective from

microstructure. _J. Appl. Phys._ 117, 084106 (2015). Article  ADS  Google Scholar  * Sun, X. X. et al. Understanding the piezoelectricity of high-performance potassium sodium niobate

ceramics from diffused multi-phase coexistence and domain feature. _J. Mater. Chem. A_ 7, 16803 (2019). Article  CAS  Google Scholar  * Zheng, T. et al. Electric field compensation effect

driven strain temperature stability enhancement in potassium sodium niobate ceramics. _Acta Mater._ 182, 1 (2019). Article  ADS  CAS  Google Scholar  * Zhang, N. et al. Potassium sodium

niobate ceramics with broad phase transition range: temperature-insensitive strain. _Ceram. Inter._ 45, 24827 (2019). Article  CAS  Google Scholar  * Yao, F. Z. et al. Diffused phase

transition boosts thermal stability of high-performance lead-free piezoelectrics. _Adv. Funct. Mater._ 26, 1217 (2016). Article  CAS  Google Scholar  * Zhang, M. H. et al. High and

temperature-insensitive piezoelectric strain in alkali niobate lead-free perovskite. _J. Am. Chem. Soc._ 139, 3889 (2017). Article  CAS  PubMed  Google Scholar  * Li, P. et al. High

piezoelectricity and stable output in BaHfO3 and (Bi0.5Na0.5)ZrO3 modified (K0.5Na0.5)(Nb0.96Sb0.04)O3 textured ceramics. _Acta Mater._ 199, 542 (2020). Article  ADS  CAS  Google Scholar  *

Hwang, S. Y. et al. Enhanced thermal stability by short-range ordered ferroelectricity in K0.5Na0.5NbO3-based piezoelectric oxides. _Mater. Horiz._ 10, 2656 (2023). Article  CAS  PubMed 

Google Scholar  * Wang, K. et al. Temperature-insensitive (K, Na)NbO3-based lead-free piezoactuator ceramics. _Adv. Funct. Mater._ 23, 4079 (2013). Article  CAS  Google Scholar  * Song, A.

Z. et al. Simultaneous enhancement of piezoelectricity and temperature stability in KNN-based lead-free ceramics via layered distribution of dopants. _Adv. Funct. Mater._ 32, 2204385 (2022).

Article  CAS  Google Scholar  * Xi, K. B. et al. Diffuse multiphase coexistence renders temperature-insensitive lead-free energy-harvesting piezoceramics. _J. Mater. Chem. A_ 11, 3556

(2023). Article  CAS  Google Scholar  * Wang, D. W. et al. Composition and temperature dependence of structure and piezoelectricity in (1-x)(K1-yNay)NbO3-x(Bi1/2Na1/2)ZrO3 lead-free

ceramics. _J. Am. Ceram. Soc._ 100, 627 (2017). Article  CAS  Google Scholar  * Zheng, T. et al. Compositionally graded KNN-based multilayer composite with excellent piezoelectric

temperature stability. _Adv. Mater._ 34, 2109175 (2022). Article  CAS  Google Scholar  * Messing, G. L. et al. Templated grain growth of textured piezoelectric ceramics. _Crit. Rev. Solid

State_ 29, 45 (2004). Article  CAS  Google Scholar  * Kimura, T. Application of texture engineering to piezoelectric ceramics-a review. _J. Ceram. Soc. Jpn._ 114, 15–25 (2006). Article 

Google Scholar  * Li, P. et al. Ultrahigh piezoelectric properties in textured (K, Na)NbO3-based lead-free ceramics. _Adv. Mater._ 30, 1705171 (2018). Article  ADS  Google Scholar  * Lin, J.

F. et al. Ultrahigh energy harvesting properties in temperature-insensitive eco-friendly high-performance KNN-based textured ceramics. _J. Mater. Chem. A_ 10, 7978 (2022). Article  CAS 

Google Scholar  * Liu, Q. et al. Niobate-based lead-free piezoceramics: a diffused phase transition boundary leading to temperature-insensitive high piezoelectric voltage coefficients. _J.

Mater. Chem. C_ 6, 1116 (2017). Article  Google Scholar  * Lotgering, F. K. Topotactical reactions with ferrimagnetic oxides having hexagonal crystal structures-I. _J. Inorg. Nucl. Chem._ 9,

113 (1959). Article  CAS  Google Scholar  * Lv, X. et al. Tailoring micro-structure of eco-friendly temperature-insensitive transparent ceramics achieving superior piezoelectricity. _ACS

Appl. Mater. Interfaces_ 12, 49795–49804 (2020). 44. Article  CAS  PubMed  Google Scholar  * Lin, J. F. et al. Tailoring micro-structure of eco-friendly temperature-insensitive transparent

ceramics achieving superior piezoelectricity. _Acta Mater._ 235, 118061 (2022). Article  CAS  Google Scholar  * Wu, J. G. Perovskite lead-free piezoelectric ceramics. _J. Appl. Phys._ 127,

190901 (2020). Article  ADS  CAS  Google Scholar  * Xing, J. et al. High performance BiFe0.9Co0.1O3 doped KNN-based lead-free ceramics for acoustic energy harvesting perovskite lead-free

piezoelectric ceramics. _Nano Energy_ 84, 105900 (2021). Article  CAS  Google Scholar  * Tao, H. et al. Ultrahigh performance in lead-free piezoceramics utilizing a relaxor slush polar state

with multiphase coexistence. _J. Am. Chem. Soc._ 141, 13987 (2019). Article  CAS  PubMed  Google Scholar  * Li, P. et al. High-performance potassium-sodium niobate lead-free piezoelectric

ceramics based on polymorphic phase boundary and crystallographic texture. _Acta Mater._ 165, 486–495 (2019). Article  ADS  CAS  Google Scholar  * Liu, W. F. et al. Large piezoelectric

effect in Pb-free ceramics. _Phys. Rev. Lett._ 103, 257602 (2009). Article  ADS  PubMed  Google Scholar  * Feng, Y. et al. Defect engineering of lead-free piezoelectrics with high

piezoelectric properties and temperature-stability. _ACS Appl. Mater. Interfaces_ 8, 9231–9241 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Watson, B. H. et al. Textured Mn-doped

PIN-PMN-PT ceramics: harnessing intrinsic piezoelectricity for high-power transducer applications. _J. Eur. Ceram. Soc._ 41, 1270–1279 (2021). Article  CAS  Google Scholar  * Yang, W. W. et

al. A Study on the relationship between grain size and electrical properties in (K, Na)NbO3-based lead-free piezoelectric ceramics. _Adv. Electron. Mater._ 5, 1900570 (2019). Article  CAS 

Google Scholar  * Qian, J. et al. Topological vortex domain engineering for high dielectric energy storage performance. _Adv. Energy Mater._ 14, 2303409 (2024). Article  CAS  Google Scholar

  * Jiang, J. et al. Novel lead-free NaNbO3-based relaxor antiferroelectric ceramics with ultrahigh energy storage density and high efficiency. _J. Mater._ 8, 295–301 (2022). Google Scholar

  * Qian, J. et al. High energy storage performance and large electrocaloric response in Bi0.5Na0.5TiO3-Ba(Zr0.2Ti0.8)O3 thin films. _ACS Appl. Mater. Interfaces_ 14, 54012–54020 (2022).

Article  CAS  PubMed  Google Scholar  * Skidmore, T. A. et al. Temperature stability of ([Na0.5K0.5NbO3]0.93-[LiTaO3]0.07) lead-free piezoelectric ceramics. _Appl. Phys. Lett._ 94, 222902

(2009). Article  ADS  Google Scholar  * Zhang, H. B. et al. Temperature-insensitive electric-field-induced strain and enhanced piezoelectric properties of <001> textured (K,

Na)NbO3-based lead-free piezoceramics. _Acta Mater._ 156, 389 (2018). Article  ADS  CAS  Google Scholar  * Quan, Y. et al. Large piezoelectric strain with superior thermal stability and

excellent fatigue resistance of lead-free potassium sodium niobate-based grain orientation-controlled ceramics. _ACS Appl. Mater. Interfaces_ 10, 10220 (2018). Article  CAS  PubMed  Google

Scholar  * Xu, M. S. et al. Large-area flexible memory arrays of oriented molecular ferroelectric single crystals with nearly saturated polarization. _Small_ 18, 2203882 (2022). Article  CAS

  Google Scholar  * Wang, R. P. et al. Temperature stability of lead-free niobate piezoceramics with engineered morphotropic phase boundary. _J. Am. Ceram. Soc._ 98, 2177–2182 (2015).

Article  CAS  Google Scholar  * Acosta, M. et al. Relationship between electromechanical properties and phase diagram in the Ba(Zr0.2Ti0.8)O3-x(Ba0.7Ca0.3)TiO3 lead-free piezoceramic. _Acta

Mater._ 80, 48–55 (2014). Article  CAS  Google Scholar  * Li, F. et al. Investigation of electromechanical properties and related temperature characteristics in domain-engineered tetragonal

Pb(In1/2Nb1/2)O3-Pb(Mg1/3Nb2/3)O3-PbTiO3 crystals. _J. Am. Ceram. Soc._ 93, 2731–2734 (2010). Article  CAS  Google Scholar  * Li, J. L. et al. Lead zirconate titanate ceramics with aligned

crystallite grains. _Science_ 380, 87–93 (2023). Article  ADS  CAS  PubMed  Google Scholar  * Shi, X. M. et al. Quantitative investigation of polar nanoregion size effects in relaxor

ferroelectrics. _Acta Mater._ 237, 118147 (2022). Article  CAS  Google Scholar  * Pohlmann, H. et al. A thermodynamic potential and the temperature-composition phase diagram for

single-crystalline K1-xNaxNbO3 (0 ≤ x ≤ 0.5). _Appl. Phys. Lett._ 110, 102906 (2017). Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the

National Natural Science Foundation of China under Grant (Nos. 52032007, 51772211, and 52172128) and the National Key R&D Program of China (2021YFB3201100). We thank the Instrument

Analysis Center of Xi’an Jiaotong University for assistance with electron microscopy characterization. AUTHOR INFORMATION Author notes * These authors contributed equally: Lihui Xu, Jinfeng

Lin, Yuxuan Yang. AUTHORS AND AFFILIATIONS * School of Materials Science and Engineering, Tongji University, Shanghai, China Lihui Xu, Jinfeng Lin, Guanglong Ge, Jin Qian, Cheng Shi, Guohui

Li, Simin Wang, Bo Shen & Jiwei Zhai * State Key Laboratory for Mechanical Behavior of Materials, Xi’an Jiaotong University, Xi’an, PR China Yuxuan Yang, Zhihao Zhao, Yang Zhang, Haijun

Wu, Fei Li, Xiangdong Ding & Jun Sun * Department of Physics, University of Science and Technology Beijing, Beijing, China Xiaoming Shi * School of Materials Science and Engineering,

Liaocheng University, Liaocheng, China Peng Li * Chinese Acad Sci, Shanghai Inst Ceram, State Key Lab High Performance Ceram & Superfine, Shanghai, China Zhengqian Fu * School of

Materials Science and Engineering, Beijing Institute of Technology, Beijing, China Houbing Huang Authors * Lihui Xu View author publications You can also search for this author inPubMed 

Google Scholar * Jinfeng Lin View author publications You can also search for this author inPubMed Google Scholar * Yuxuan Yang View author publications You can also search for this author

inPubMed Google Scholar * Zhihao Zhao View author publications You can also search for this author inPubMed Google Scholar * Xiaoming Shi View author publications You can also search for

this author inPubMed Google Scholar * Guanglong Ge View author publications You can also search for this author inPubMed Google Scholar * Jin Qian View author publications You can also

search for this author inPubMed Google Scholar * Cheng Shi View author publications You can also search for this author inPubMed Google Scholar * Guohui Li View author publications You can

also search for this author inPubMed Google Scholar * Simin Wang View author publications You can also search for this author inPubMed Google Scholar * Yang Zhang View author publications

You can also search for this author inPubMed Google Scholar * Peng Li View author publications You can also search for this author inPubMed Google Scholar * Bo Shen View author publications

You can also search for this author inPubMed Google Scholar * Zhengqian Fu View author publications You can also search for this author inPubMed Google Scholar * Haijun Wu View author

publications You can also search for this author inPubMed Google Scholar * Houbing Huang View author publications You can also search for this author inPubMed Google Scholar * Fei Li View

author publications You can also search for this author inPubMed Google Scholar * Xiangdong Ding View author publications You can also search for this author inPubMed Google Scholar * Jun

Sun View author publications You can also search for this author inPubMed Google Scholar * Jiwei Zhai View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS Conceptualization: X.L.H., L.J.F. Data curation: X.L.H. Methodology: X.L.H., L.J.F., S.X.M., F.Z.Q., L.P. Investigation: X.L.H. Funding acquisition: Z.J.W., S.B., W.H.J.

Project administration: X.L.H., L.J.F., Y.Y.X., Z.Z.H., S.X.M., G.G.L., Q.J., S.C., L.G.H., W.S.M., Z.Y. Supervision: S.B., W.H.J., L.F., H.H.B., Ding X.D., S.J., Z.J.W. Writing - original

draft: X.L.H. Writing - review & editing: X.L.H., L.J.F., Y.Y.X., S.X.M., W.H.J., Z.J.W. CORRESPONDING AUTHORS Correspondence to Bo Shen, Haijun Wu, Houbing Huang or Jiwei Zhai. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_ thanks Jung Woo Lee, Yuho Min, C. Siva, and the other

anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with

regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION LASING REPORTING SUMMARY PEER REVIEW FILE SOURCE DATA

SOURCE DATA RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any

non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the

Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of

it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material

is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission

directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Xu,

L., Lin, J., Yang, Y. _et al._ Ultrahigh thermal stability and piezoelectricity of lead-free KNN-based texture piezoceramics. _Nat Commun_ 15, 9018 (2024).

https://doi.org/10.1038/s41467-024-53437-5 Download citation * Received: 20 June 2024 * Accepted: 12 October 2024 * Published: 18 October 2024 * DOI:

https://doi.org/10.1038/s41467-024-53437-5 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative