Reader TTS

ABSTRACT Metal-free organic perovskite ferroelectric materials have been shown recently to have a number of attractive properties, including high spontaneous polarization and piezoelectric

coefficients. In particular, slow evaporation of solutions containing organic amines, inorganic ammoniums, and dilute hydrohalogen acid has been shown to produce several attractive materials

in the MDABCO-NH4-I3 family (MDABCO is N-methyl-N’-diazabicyclo[2,2,2] octonium). In the present work, we study by first-principles calculations the origin of polarizaiton, electronic

density of state, piezoelectric response, and elastic properties of MDABCO-NH4-X3 (X = Cl, Br, I). We find that the dipole moments of the MDABCO and NH4 groups are negligible, and the large

spontaneous polarization of MDABCO-NH4-I3 mainly results from MDABCO and NH4 being off-center relative to I ions. Although the piezoelectric response of organic materials is usually very

weak, we observe large piezoelectric strain components, _d__x_4 and _d__x_5; the calculated _d__x_5 is 119 pC/N for MDABCO-NH4-Cl3, 248 pC/N for MDABCO-NH4-Br3 and 178 pC/N for

MDABCO-NH4-I3. The large value of _d__x_5 is found to be closely related with the large value of elastic compliance tensor, _s_44. These results show that MDABCO-NH4-X3 metal-free organic

perovskites have large piezoelectric response with soft elastic properties. SIMILAR CONTENT BEING VIEWED BY OTHERS TUNABLE FERROELECTRICITY IN OXYGEN-DEFICIENT PEROVSKITES WITH GRENIER

STRUCTURE Article Open access 09 December 2023 ANALYZING THE STRUCTURAL, OPTOELECTRONIC, AND THERMOELECTRIC PROPERTIES OF INGEX3 (X = BR) PEROVSKITES VIA DFT COMPUTATIONS Article Open access

09 October 2024 INTERCALATION-DRIVEN FERROELECTRIC-TO-FERROELASTIC CONVERSION IN A LAYERED HYBRID PEROVSKITE CRYSTAL Article Open access 03 June 2022 INTRODUCTION The perovskite structures

have been dubbed a “chameleon” due to their rich diversity of chemical compositions and physical properties.1,2,3 Searching for large piezoelectric perovskites has been the aspiration of

science and engineering studies.4 Compared with inorganic perovskite, organic materials possess many advantages. For example, organic crystals can be synthesized at relatively low

temperature.5 The easy reorientation inorganic cations make them promising candidates for order–disorder ferroelectrics.6,7 By replacing Pb and other toxic ions with inorganic cations, they

can be designed to toxic-metal-free materials. Therefore, organic materials have become an attractive topic not only due to the remarkable structural variability and highly tunable

properties, but also due to their potential applications in light sources, photovoltaics, and electronics.8 Recently, a breakthrough of piezoelectric material was reported by Yu-Meng You,

Ren-Gen Xiong, and colleagues.9 Based on molecular design strategy and elaborate organic cation selection, they successfully synthesized a family of metal-free organic perovskite

ferroelectrics. This family contains 23 new compounds, in which 21 compounds have cubic perovskite structure and the other two have hexagonal perovskite structure. Among these cubic

perovskite compounds, 14 compounds show paraelectric-ferroelectric transition and their Curie temperatures range from 355 to 493 K. This means all of them are ferroelectric at room

temperature. The general formula of this family is A(NH4)X3, in which A is a divalent organic cation and X is halogen anion. Despite their diversity, compounds of this family were obtained

easily by a simple strategy: slow evaporation of solution containing organic ammines, inorganic ammoniums, and dilute hydrohalogen acid. Not only the facile synthesis method but also their

desirable properties make them are possible for application in flexible devices. Among this metal-free organic perovskite family, MDABCO-NH4-I3 (MDABCO is

N-methyl-N’-diazabicyclo[2,2,2]octonium) is an outstanding one. Its ferroelectric Curie temperature (_T_0) is 448 K, spontaneous polarization (_P_s) is 22 μC/cm2 and piezoelectric

coefficient _d_33 (along [1 1 1] direction) is about 14 pC/N9. Furthermore, second-harmonic generation response and dielectric permittivity were also measured as a function of temperature.

Although a detailed investigation of MDABCO-NH4-I3 was made in experiment, some important physical properties were not reported. For example, except for the longitude piezoelectric stress

coefficient _d_33, other elements of piezoelectric stress tensor were not measured in experiment. Furthermore, the elastic tensor and piezoelectric strain tensor were not reported, too.

RESULTS AND DISCUSSION In order to elucidate the piezoelectric and elastic properties of MDABCO-NH4-I3, we performed the density-functional theory (DFT) calculation using

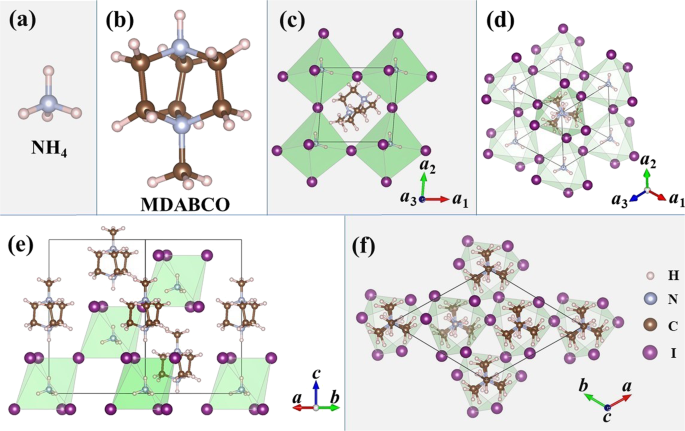
Perdew–Burke–Ernzerhof (PBE)10 and PBE-D311 methods as implemented in the Vienna ab initio simulation package (VASP).12,13,14 The primitive and conventional unit cells of MDABCO-NH4-I3 in

ferroelectric phase are depicted in Fig. 1. Herein, the MDABCO-NH4-I3 crystal is composed of three building blocks: NH4, MDABCO, and I6 octahedron. The NH4 locates in the middle of I6

octahedron, which shares corners with its six neighboring octahedra to form a three-dimensional (3D) network. The MDABCO locates in the middle of a cage defined by 12 iodine ions. It has a

trigonal structure with space group _R_3. The three-fold axis passes through the two nitrogen atoms of MDABCO and the spontaneous polarization direction is parallel to this axis (_z_-axis).

Similarly with K3BO10Cl15,16,17 and trimethylchloromethyl ammonium trichloromanganese,5 it is the ordered cation MDABCO that breaks the inversion symmetry and permits the occurrence of

ferroelectric, piezoelectricity, second-harmonic generation, and other interesting phenomena. When temperature increases above 448 K, it turns to a cubic paraelectric phase.9 Besides

MDABCO-NH4-I3, MDABCO-NH4-Br3 is also successfully synthesized with similar method.9 It has a similar structure with MDABCO-NH4-I3 and exhibits paraelectric-ferroelectric transition at 390 

K. So as to calculate the properties of these newly synthesized crystal, we relaxed their atomic positions and lattice parameters first. For MDABCO-NH4-I3 and MDABCO-NH4-Br3, we used the

experimental data for their initial structures. Then, lattice parameters and atomic positions are relaxed without any symmetry constraint until calculated stresses and forces are less than

the threshold. As MDABCO-NH4-Cl3 is not synthesized in experiment, we substitute the Br in MDABCO-NH4-Br3 to Cl as its initial structure.18,19 Then, we relaxed lattice parameters and atomic

positions of MDABCO-NH4-Cl3 until they meet the threshold. So as to verify the calculated structure are stable, we calculated their zone center phonon frequencies and do not find unstable

mode. Moreover, they all satisfy the mechanical stability criteria, namely, that the stiffness tensor is positive-definite.20 The calculated lattice parameters of primitive unit cell are

listed in Table 1 and are compared with available experimental data. Because MDABCO-NH4-X3 are molecular materials, we use the DFT-D3 method to take the van de Waals interaction into

consideration.9 Unfortunately, PBE + D3 does not give better result compared with PBE. As far as the angle is concerned, PBE functional is slightly better than PBE + D3. However, when it

comes to the lattice length, PBE functional performs much better than PBE + D3. The PBE result overestimates the lattice parameter of MDABCO-NH4-I3 1.5%, and PBE + D3 underestimates 1.9%.

For MDABCO-NH4-Br3, PBE underestimates lattice parameter 2.1%, while PBE + D3 underestimates it as large as 5.2%. This means PBE is more suitable than PBE + D3 in MDABCO-NH4-X3 calculation.

The poor performance of PBE-D3 is due to the hydrogen bond in MDABCO-NH4X3. The total energy of DFT-D3 is _E_KS-DFT − _E_disp.11 The first term _E_KS-DFT is the usual self-consistent KS

energy and the second term _E_disp is the dispersion correction. This correction is a sum of two- and three-body energies, related with bond length, bond angle and etc. However, it has no

relationship with the electronic band structure. Therefore, the developers of DFT-D3 says “the method is of molecular mechanics type in the sense that it is very fast and only geometric

information is employed”.11 It is pointed in refs. 21,22,23,24 that the long-range part of the exchange contribution is overestimated in PBE. This overestimation compensates the missing vdW

interaction to some extent. Consequently, directly adding additional dispersion correction to PBE would lead to an unphysical ‘double-counting’’ effect.22 As shown in ref. 11, this

unphysical effect in hydrogen bond is severe and results into the poor performance of PBE-D3. Therefore, we use the atom position and lattice parameters of PBE and calculate other properties

with PBE functional as well. So as to investigate the origin of large spontaneous polarization (22 μC/cm2) of MDABCO-NH4-I3, we calculate its Born effective charge (BEC). BEC is a

second-order tensor and the component along the dipole direction is related with ferroelectric polarization. The calculated BEC components along the dipole direction are marked in Fig. 2. As

shown in Fig. 2a, MDABCO can be divide into three parts. The top hydrogen, the bottom CH3 and the middle N2C6H12 part. Their BECs are +0.84, +0.81, and +0.77, respectively. For MDABCO, all

C and H show positive values, only N shows negative values. We calculate the positive and negative charge centers of MDABCO, and find the distance between the two centers is as small as

0.009 Å. They are almost overlap with each other. Therefore, the dipole moment of the MDABCO group is negligible. The total charge of MDABCO is +2.45 and the total charge center is marked as

a red point in Fig. 2. The positive and negative charge centers of NH4 are almost overlap with each other, too. Therefore, the dipole moment of the NH4 group is negligible. The total charge

of NH4 is +1.15, centered at the N position. The charge of I is −1.2, similar to its formal charge −1. The relative positions of MDABCO, NH4, and I3 along the dipole moment direction are

depicted in Fig. 2b. It is clear that the charge center of MDABCO (A-site of perovskite) shifts upward with the distance _d_A = (5.37 – 3.84)/2 = 0.765 Å relative to the center of its

nearest neighboring six I− ions. At the same time, the charge center of NH4 (B-site of perovskite) shifts upward, too, with the distance _d_B = (2.83 – 1.77)/2 = 0.53 Å relative to the

center of I6 octahedron. As a comparison, the A-site and B-site displacements of rhombohedral BaTiO3 are 0.10 and 0.19 Å, respectively. They are much smaller than the corresponding

off-center distance of MDABCO-NH4-I3. Furthermore, _d_A is larger than _d_B for MDABCO-NH4-I3, similarly to the condition of PbTiO3. This means that MDABCO-NH4-I3 is an A-site driven

ferroelectricity. On the contrary, _d_A is smaller than _d_B for BaTiO3, indicating a B-site driven ferroelectricity. Therefore, MDABCO-NH4-I3 is an A-site driven order–disorder

ferroelectricity and its large polarization results from the large off-center distances of MDABCO and NH4 relative to I. As shown in the dashed lines of Fig. 2b, there are three hydrogen

bonds between three hydrogens of CH3 and three I− anions. And there are also three hydrogen bonds between three hydrogens of NH4 and its surrounding three I− anions.9 When MDABCO-NH4-I3

turns from ordered ferroelectric phase to disordered paraelectric phase, much energy is needed to break these six hydrogen bonds so as to make MDABCO and NH4 rotating freely. In paraelectric

phase, the rotating MDABCO must overcome a barrier, in which the two N atoms of MDABCO lines along the [1 1 0] direction. So as to get the barrier value, we calculate the total energy of

two configurations. In the first configuration, lattice parameters are set to the experimental value of paraelectric phase and I ions forms a cubic network. Then we fix the positions of I

and set the two N and two C atoms of MDABCO along the C3 axis to move only along the [1 1 1] direction. Other atoms can move freely. In the second configuration, lattice parameters and

positions of I ions are the same as configuration one. Then the selected two N and two C atoms of MDABCO in the first configuration are set to move only along the [1 1 0] direction. Other

atoms can move freely. The energy difference between the above two configurations is Δ_E_ = 0.156 eV per primitive unit cell. As MDABCO is polyatomic molecules with six freedom (three

translations and three rotations), the energy barrier corresponds to the temperature _T_ = Δ_E_/(3 × _k_B) = 398 K, which agrees with the experimental value 448 K. The structure evolution

with X ions is presented in four parts. Firstly, the structure parameters inner MDABCO are shown in Fig. 3a. The bond lengths (solid red symbol) refer to the left axis, while the bond angles

(open blue symbol) correspond to the right axis. With halogen changing from Cl to I, the bond lengths change less than 0.01 Å and the bond angles change <0.2° Therefore, the MDABCO group

performs like a rigid body in MDABCO-NH4-X3 crystals. Secondly, the structure parameters between MDABCO and its surrounding X ions are shown in Fig. 3b. There are two kinds of bond length

between H and X ions. The first one is _d_HX_w at the top of Fig. 3b inset, while the second one is _d_HX_s at the bottom of Fig. 3b inset (the subscript ‘w’’ and ‘s’’ represent ‘relatively

weak’’, and ‘relatively strong’’). The first bond length is larger than the second one, indicating the first hydrogen–halogen interaction is weaker than the second one. With the radius of X

ion increases from Cl to I, the two hydrogen-X bond lengths increase. We also give the angles between H–X bond and the X3 plane (inset of Fig. 3b). With halogen changing from Cl to I, the

angle _θ_HX3_w changes from 26.4° to 31.1°, increasing 4.7°. However, the angle _θ_HX3_s changes from 46.4° to 44.4°, decreasing 2.2°. The opposite trends of _θ_HX3_w and _θ_HX3_s originate

from the A-site space changing of perovskite. With ion changing from Cl− to I−, the lattice parameter of MDABCO-NH4-X3 increases from 6.84 to 7.37 Å. Then, the corresponding A-site space of

perovskite increases. In MDABCO-NH4-Cl3, the MDABCO group is a little compressed as there is not enough room for it. When it comes to MDABCO-NH4-I3, there is spare room for MDABCO group.

Because the hydrogen–halogen interaction at the bottom of Fig. 3b inset is stronger than the top one, the bottom hydrogen approaches its neighboring I, decreasing _θ_HX3_s, while the top

hydrogen leaves its neighboring I, increasing _θ_HX3_w. Thirdly, we give the structure parameters inner NH4 in Fig. 4a. There are two N–H bond length: _l_NH_up and _l_NH_dn. The first bond

almost points to the neighboring X ion, while the second bond points to the middle of three X ions. Therefore, the first N–H bond is enlarged by X ions relative to the second one, resulting

into _l_NH_up > _l_NH_dn. Because NH4 forms a tetrahedron, we calculate the Baur’s distortion index _D_ with the following equation17,25: $$D = \frac{1}{n}\mathop {\sum}\limits_{i = 1}^n

{\frac{{|l_i - l_{{\mathrm{av}}}|}}{{l_{{\mathrm{av}}}}}}$$ (1) where _l__i_ is the distance from the central atom to the _i_th coordinating atom, and _l_av is the average bond length. For a

regular tetrahedron, the distortion index equals zero. For NH4 tetrahedron, the distortion index is very little, indicating that NH4 performs like a rigid body in MDABCO-NH4-X3. Fourthly,

we show the structure parameters between NH4 and its surrounding X ions in Fig. 4b. For a regular octahedron, N atom should locate at the center and _Φ_XNX should be 180°. Actually, the

angle _Φ_XNX is about 157°, obviously deviating from the ideal value of 180°. With halogen changing from Cl to I, _Φ_XNX changes from 154.6° to 158.7°, increasing 4.1°. Similarly with

MDABCO, we also give the angles between H–X bond and the X3 plane (inset of Fig. 4b). With halogen changing from Cl to I, the angle _Φ_HX3_w changes from 36.0° to 33.8°, decreasing 2.2°.

However, the angle _Φ_HX3_s changes from 30.6° to 33.2°, increasing 2.6°. With halogen changing from Cl to I, the evolutions of _Φ_HX3_s (increasing) and _Φ_HX3_w (decreasing) are opposite

to those of _θ_HX3_s (decreasing) and _θ_HX3_w (increasing). It originates from the B-site space changing of perovskite. With X ion changing from I− to Cl− (not Cl− to I−), the B-site space

of perovskite increases. In MDABCO-NH4-I3, the NH4 group is a little compressed as there is not enough room for it. When it comes to MDABCO-NH4-Cl3, there is spare room for NH4 group.

Because the hydrogen–halogen interaction at the top of Fig. 4b inset is stronger than the bottom one, the top hydrogen approaches its neighboring Cl, decreasing _θ_HX_s, while the bottom

hydrogen leaves its neighboring Cl, increasing _θ_HX_w. The calculated electronic density of state (DOS) of MDABCO-NH4-X3 are exhibited in Fig. 5. It can be clearly seen that these DOS are

divided into three parts. The low energy part (below −2 eV) is mainly composed of occupied N-2_p_, C-2_p_, and H-1_s_ states, the middle energy part (from −2 to 0 eV) is mainly composed of

occupied Cl-3_p_, Br-4_p_, and I-5_p_ states, and the high energy parts (above 3 eV) is unoccupied states of N, C, H, and halogen. By comparing Fig. 5a–c, we can see two obvious evolutions

with anion changes from Cl− to I−. Firstly, the width of the occupied halogen _p_ orbital increases from 0.8 (Cl−) to 1.1 (I−) eV. This width broadening originates from the X-N-X angle

changing in Fig. 4b. With X ion changing from Cl− to I−, the angle of X-N-X angle (_Φ_XNX) increases toward 180°, resulting into more electron interaction along the X-N-X line.26 Secondly,

there are obvious gap between the occupied halogen _p_ state and the occupied states of C, N, and H. This characters indicate the halogen interactions with MDABCO and NH4 are weak.16,27 It

agrees with the analysis of Figs. 3a and 4a. Piezoelectric effect allows interconversion between electric field and mechanical deformation. This property is important for applications of

sensors, actuators, vibration reducer, and so on. Conventional perovskite ferroelectrics usually require high processing temperatures,18 have little mechanical flexibility, and even contain

potential toxic elements.4 These drawbacks make scientists pay much attention to organic materials.5,9 Experiment shows that MDABCO-NH4-I3 is an organic piezoelectrics without metal element.

The piezoelectric strain coefficient _d_z3 of MDABCO-NH4-I3 is measure to be ~14 pC/N at room temperature.9 However, other components of piezoelectric tensor are still unknown. Therefore,

we calculated the piezoelectric strain and stress tensors of MDABCO-NH4-X3. The crystallographic symmetry plays an important role in the piezoelectric phenomena.28 According to the

definition of the piezoelectric effect, in the matrix notation (with two indices), the piezoelectric strain tensor _d_ij of MDABCO-NH4-X3 (space group _R_3) is $$\left[

{\begin{array}{*{20}{c}} {d_{x1}} & { - d_{x1}} & 0 & {d_{x4}} & {d_{x5}} & { - 2d_{y2}} \\ { - d_{y2}} & {d_{y2}} & 0 & {d_{x5}} & { - d_{x4}} & { -

2d_{x1}} \\ {d_{z1}} & {d_{z1}} & {d_{z3}} & 0 & 0 & 0 \end{array}} \right]$$ The corresponding piezoelectric stress tensor _e_ij is $$\left[ {\begin{array}{*{20}{c}}

{e_{x1}} & { - e_{x1}} & 0 & {e_{x4}} & {e_{x5}} & { - e_{y2}} \\ { - e_{y2}} & {e_{y2}} & 0 & {e_{x5}} & { - e_{x4}} & { - e_{x1}} \\ {e_{z1}} &

{e_{z1}} & {e_{z3}} & 0 & 0 & 0 \end{array}} \right]$$ There are six independent coefficients in piezoelectric strain (stress) tensor. The piezoelectric strain tensor is

defined as the ratio of developed strain to the applied electric field.28 Our calculated piezoelectric strain tensors are shown in Fig. 6a. The calculated _d_z3 of MDABCO-NH4-I3 is 14.4 

pC/N, which agrees very well with the experimental value ~14 pC/N9. This agreement proves the validity of our calculation. The calculated _d__x_4 and _d__x_5 are much larger than _d_z3. The

largest components of piezoelectric strain tensor for the three crystals are all _d__x_5, which is 119 p_C_/_N_ for MDABCO-NH4-Cl3, 248 p_C_/_N_ for MDABCO-NH4-Br3, and 179 p_C_/_N_ for

MDABCO-NH4-I3. They are much larger than the largest component of inorganic crystals, such as lithium niobate (_d__x_5 = 68 pC/N),29 lithium tantalite (_d__x_5 = 26 pC/N),29 cadmium sulfide

(_d__x_5 = -14 pC/N),30 barium sodium niobate (_d__y_4 = 52 pC/N),28 hexagonal zinc oxide (_d__z_3 = 12.4 pC/N),31 and hexagonal zinc sulfide (_d__z_3 = 3.2 pC/N).32,33 They are even

comparable with that of barium titanate (_d__x_5 = 242 pC/N)34 and are almost one third of that of PZT-5H (_d__x_5 = 741 pC/N).34 The above comparison shows that MDABCO-NH4-X3 have large

piezoelectric responds and are good candidate materials for a variety of piezoelectric applications. Similarly with piezoelectric strain tensor, piezoelectric stress tensor is defined as the

ratio of developed stress to the applied electric field.28 Our calculated piezoelectric stress tensors are shown in Fig. 6b. Except for _e_x1 and _e_z3, the other components change little

with X anion. Furthermore, differently with the condition of _d__x_5, _e__x_5 is not the largest component of piezoelectric stress tensor. It is well known that the piezoelectric strain

tensor [_d_], piezoelectric stress tensor [_e_], and elastic compliance tensor [_s_] satisfy the relation [_d_] = [_e_][_s_].28 This indicates that the large value of _d__x_5 may originates

from the large elastic compliance. In the matrix notation (with two indices), the elastic compliance tensor of MDABCO-NH4-X3 (space group _R_3) is $$\left[ {\begin{array}{*{20}{c}} {s_{11}}

& {s_{12}} & {s_{13}} & {s_{14}} & { - s_{25}} & 0 \\ {s_{12}} & {s_{11}} & {s_{13}} & { - s_{14}} & {s_{25}} & 0 \\ {s_{13}} & {s_{13}} &

{s_{33}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {s_{44}} & 0 & {2s_{25}} \\ { - s_{25}} & {s_{25}} & 0 & 0 & {s_{44}} & {2s_{14}} \\ 0 & 0 & 0

& {2s_{25}} & {2s_{14}} & {2(s_{11} - s_{12})} \end{array}} \right]$$ There are seven independent coefficients in elastic compliance tensor. The calculated values are shown in

Fig. 7. It is clear in Fig. 7 that the _s_44 is the largest component in MDABCO-NH4-X3. With X anion changes from Cl− to I−, it firstly increases from 449 to 658 and then decreases to 473 × 

10−12 m2/N. This evolution is similar with that of _d__x_5 in Fig. 6a. For MDABCO-NH4-X3, the piezoelectric strain tensor component _d__x_5 = _e__x_5 × _s_44 − 2_e__x_1 × _s_25 − 2_e_y2 × 

_s_14. The last term 2_e_y2 × _s_14 is about two orders smaller than the first term, and the second term 2_e__x_1 × _s_25 is about one-third of the first term. Because the _e_x5 difference

for MDABCO-NH4-X3 is rather small, the _d__x_5 evolution with halogen is dominated by _s_44. For MDABCO-NH4-X3, _s_44 equals (_c_12 − _c_11)/(2_c_214 + 2_c_225 − _c_11_c_44 + _c_12_c_44),

related with five parameters _c_12, _c_11, _c_14, _c_25, and _c_44. No one dominates the others. Therefore, _s_44 is affected by many structure parameters. So as to give an intuitive

explanation, we propose a model based on the tolerance factor of perovskite. For an inorganic perovskite ABX3, the Goldschmidt tolerance factor (TF) is defined as below35 $${\mathrm{TF}} =

\frac{{r_{\mathrm{A}} + r_{\mathrm{X}}}}{{\sqrt 2 \left( {r_{\mathrm{B}} + r_{\mathrm{X}}} \right)}}$$ (2) where _r_A, _r_B, and _r_X are the ionic radii of the ions A, B, and X,

respectively. In this model, all ions are assumed to be hard spheres. TF is widely used to analysis the structure of inorganic perovskite.36 TF = 1 corresponds to an ideal cubic perovskite

with A, B and X ions touching each other perfectly. TF > 1 implies that A cation is too large or B cation too small, while TF < 1 implies A cation is too small or B cation too large.

This concept is generalized to hybrid perovskites containing organic cations by Kieslich and Becker et al.37,38,39 It is found that the TF value of most hybrid perovskites lies in the range

from 0.8 to 1. Hybrid perovskite structures with TF > 1 or TF < 0.8 are rarely observed.39 So as to get the TF values of MDABCO-NH4-X3, ions radii are needed. The Shannon radius of

Cl−, Br−, and I− are 1.81, 1.96, and 2.2 Å, respectively.40 The radius of (NH4)+ is proposed to be 1.46 Å39. But the radius of MDABCO is difficult to define because it is not a hard sphere.

Based on the available radii of X and NH4, we calculate the TF value evolution with MDABCO radius (_r_A). As shown in Fig. 8a, the TF value of MDABCO-NH4-Cl3 is the largest, while that of

MDABCO-NH4-I3 is the smallest. In experiment, MDABCO-NH4-Br3 and MDABCO-NH4-I3 are successful synthesized, while MDABCO-NH4-Cl3 is not. Therefore, it is reasonable to assume that the TF

values of MDABCO-NH4-Br3 and MDABCO-NH4-I3 is <1, while that of MDABCO-NH4-Cl3 is >1 (the middle light blue region of Fig. 8a). This assumption agrees with the angles analysis of Figs.

3b and 4b. We also give the sketch of AX plane and BX plane for different TF values in Fig. 8b–d. For TF > 1, the A cation is too large, resulting into over compression between A and X

ions. It is the condition of MDABCO-NH4-Cl3. For TF < 1, the B cation is too large, resulting into over compression between B and X ions. It is the condition of MDABCO-NH4-I3. The over

compressions of MDABCO-NH4-Cl3 and MDABCO-NH4-I3 increase their shear resistance, reducing their _s_44 values. For MDABCO-NH4-Br3, its TF value is closer to 1 than that of MDABCO-NH4-I3. It

implies there is less over compression between A and X ions or B and X ions in MDABCO-NH4-Br3. Consequently, its shear resistance is less than that of MDABCO-NH4-Cl3 and MDABCO-NH4-I3,

resulting in large _s_44 value. The large elastic compliance tensor in Fig. 7 suggests that MDABCO-NH4-X3 are soft materials.32 So as to investigate their elastic properties, Table 2 gives

their bulk and shear moduli with Voigt-Reuss-Hill(VRH) approximation,41 which is a good estimation for mechanical properties of polycrystalline materials.16,20,42,43,44 Bulk modulus

describes the resistance of a material to a change in volume and shear modulus describes the resistance to a change in shape. Although the crystal structures of MDABCO-NH4-X3 are similar

with inorganic ABO3 perovskite, their bulk moduli are only around 10 GPa. They are much smaller than that of inorganic perovskite CaTiO3 (170.9 GPa),45 BaTiO3 (162 GPa),46,47 and PbTiO3(144 

GPa).46,47 The Young’s moduli of MDABCO-NH4-X3 are also around 10 GPa, even smaller than that of flexible metal-organic frameworks (MOFs)43: MIL-53(Al) (25.5 GPa), MIL-53(Ga) (19.2 GPa),

MIL-47 (25.3 GPa), DMOF-1(lozenge) (11.2 GPa), and DMOF-1(square) (12.5 GPa). Bulk modulus is an average value of all directions. Instead, directional Young’s modulus characterizes uniaxial

stiffness in different directions. As a reference, the directional Young’s modulus of rhombohedral BaTiO3 based on the calculated elastic stiffness using PBE functional48 are given in Fig.

9a, b. Similarly with MDABCO-NH4-X3, BaTiO3 takes rhombohedral structure as its lowest energy phase. We set its polar direction along _z_-axis. The crystal structure and directional Young’s

modulus are shown in the same view point in Fig. 9a. It is clear that the directional Young’s modulus has six local minimums and eight high value lobes. The local minimum clearly seen in

Fig. 9a is along the _A_1 direction (_A_1, _A_2, and _A_3 are the lattice vectors of the primitive unit cell). The other five local minimums are along -_A_1, ± _A_2, and ± _A_3 directions.

They correspond to compression or stretching of O–Ti–O bonds. Owing to the Ti displacement from the center of oxygen octahedron, these six directions show low rigidity. The directional

Young’s modulus viewed along the polar direction is shown in Fig. 9b. It is clear that the view direction is perpendicular to the facet of oxygen octahedron. Similarly, the other seven high

value lobes are perpendicular to the other seven facets of oxygen octahedron. Similarly with BaTiO3, the polar direction of MDABCO-NH4-X3 is parallel to _z_-axis in Fig. 9c–e. There are six

local minimums and eight high-value lobes in the directional Young’s modulus of MDABCO-NH4-X3. These local minimums are along the lattice vectors of their primitive unit cells. They

correspond to compression or stretching of X–N–X bonds in octahedrons. The directions of these high value lobes are perpendicular to the facets of X6 octahedron. Their directional Young’s

modulus can be described in the following equation42: $$\begin{array}{*{20}{l}} E \hfill & = \hfill & {1/\left[ {s_{11}sin^4\varphi + s_{33}cos^4\varphi + \left( {2s_{13} + s_{44}}

\right)sin^2\varphi {\mathrm{cos}}^2\varphi } \right.} \hfill \\ {} \hfill & {} \hfill & {\left. { + 2\left( {s_{14}{\mathrm{sin}}3\theta - s_{25}{\mathrm{cos}}3\theta }

\right){\mathrm{cos}}\,\varphi \,{\mathrm{sin}}^3\varphi } \right]} \hfill \end{array}$$ (3) where _θ_ is the azimuthal angle in the _xy_ plane from the _x_-axis (0 ≤ _θ_ < 2_π_), and _φ_

is the zenith angle from the positive _z_ axis (0 ≤ _φ_ ≤ _π_). It can be derived from Eq. (3) that _E_ equals 1/_s_33 with _φ_ = 0. The _s_33 value of MDABCO-NH4-X3 (X = Cl, Br, I) is

52.3, 60.1, and 73.9 × 10−12m2/N, respectively. Correspondingly, the highest value of the top lobe in Fig. 9c–e is 19.1, 16.6, and 13.5 GPa, respectively. When it comes to _xy_ plane, _φ_ = 

_π/2_ and _E_ = 1/_s_11. Therefore, _E_ value in the _xy_ plane has no relationship with _θ_ and becomes a circle with radius 1/_s_11. The _s_11 value of MDABCO-NH4-X3 (X = Cl, Br, I) is

110.8, 107.3, and 88.9 × 10−12 m2/N, respectively. Their corresponding circle radii in the _xy_ plane are 9.0, 9.3, and 11.2 GPa. In Eq. (3), the only term related with angle _θ_ is

(_s_14sin3_θ_ – _s_25cos3_θ_), which means _z_-axis is a threefold axis. The maximum and minimum values of this term are \(\sqrt {(s_{14}^2 + s_{25}^2)}\) and \(- \sqrt {(s_{14}^2 +

s_{25}^2)}\), respectively. Therefore, the anisotropy with angle _θ_ is only related with \(g = \sqrt {(s_{14}^2 + s_{25}^2)}\). The _g_ value of MDABCO-NH4-X3 (X = Cl, Br, I) is 112.9,

134.1, and 46.1 × 10−12 m2/N, respectively. MDABCO-NH4-Br3 has the largest _g_ value, and the _g_ value of MDABCO-NH4-I3 is much lower than the others. That is why Fig. 9e looks much

smoother than Fig. 9c, d. In summary, we calculated the structure, electronic density of state, piezoelectric response, and elastic properties of metal-free organic perovskite MDABCO-NH4-X3.

The MDABCO and NH4 groups performs like a rigid body in MDABCO-NH4-X3, and they are linked to the I6 octahedron network by H–X interaction. The high ferroelectric Curie temperature is

closely related with the break of this H–X interaction. With halogen changing from Cl to I, the tolerance factor of MDABCO-NH4-X3 increases from lower than 1 to higher than 1. Based on Born

effective charges, the calculated dipole moments of the MDABCO and NH4 groups are negligible. Therefore, the large spontaneous polarization of MDABCO-NH4-I3 mainly results from the

off-centers of MDABCO and NH4 relative to X ions. Our calculated piezoelectric strain component _d__z_3 (14.4 pC/N) of MDABCO-NH4-I3 agrees very well with experimental value (~14pC/N).

Although most organic materials have a very weak piezoelectric response, we found that some piezoelectric strain components of MDABCO-NH4-X3 have large values. Among the six independent

components, the largest one is _d__x_5. It is 119 pC/N for MDABCO-NH4-Cl3, 248 pC/N for MDABCO-NH4-Br3, and 179 pC/N for MDABCO-NH4-I3. The large value of _d__x_5 is closely related with the

large value of _s_44. This means that the large piezoelectric strain response of MDABCO-NH4-X3 is mainly originated from their softness. These unique properties of MDABCO-NH4-X3 make them

good candidates as soft, low-density and bio-friendly piezoelectrics for various important applications, such as flexible devices, implantable systems, and micro robots. METHODS we performed

the density-functional calculation using PBE10 and PBE-D311 methods as implemented in the Vienna ab initio simulation package (VASP).12,13,14 The projector-augmented wave method was used to

represent the electron–ion interaction.49 The valence-electron configurations were 2_s_22_p_2 for C, 2_s_22_p_3 for N, and n_s_2n_p_5 for halogen. The wave function was expanded in a

plane-wave basis set with an energy cutoff of 650 eV and the first Brillouin zone of primitive unit cell was sampled on a 3 × 3 × 3 mesh. The lattice parameters and atomic positions were

fully relaxed until stress and forces were <0.05 GPa and 10 meV/Å, respectively. The elastic stiffness is calculated with finite difference method.50 It applies six finite strains (three

normal and three shearing strains) to an optimized structure. All these six deformations correspond to strains of ±0.015, so as to keep strains in the elastic region. Then, the corresponding

stress are calculated and the elastic stiffness constants are obtained by the strain-stress relationship. After that, the elastic compliance is obtained by inverting the elastic stiffness

matrix directly. The piezoelectric constants, Born effective charges and zone center phonon frequencies are calculated by VASP package using density-functional perturbation theory.51 In

order to obtain these values, three kinds of perturbations are applied to a crystal. They are atomic displacement away from equilibrium position _u__i_, strain _S__j_ and electric field

_E__k_. The corresponding responses to these three perturbations are force _F__l_, stress _T__m_, and polarization _P__n_. Based on these perturbations and their responses, one can obtain

force-constant matrix d_F__l_/d_u__i_, Born effective charge d_P__n_/d_u__i_ and piezoelectric response d_P__n_/d_S__j_. DATA AVAILABILITY The data that support the findings of this study

are available from the corresponding author (Hui Wang) upon reasonable request. REFERENCES * Bhalla, A. S., Guo, R. & Roy, R. The perovskite structure—a review of its role in ceramic

science and technology. _Mater. Res. Innov._ 4, 3–26 (2016). Article  Google Scholar  * Niu, G., Guo, X. & Wang, L. Review of recent progress in chemical stability of perovskite solar

cells. _J. Mater. Chem. A_ 3, 8970–8980 (2015). Article  CAS  Google Scholar  * Bednorz, J. G. & Müller, K. A. Perovskite-type oxides—The new approach to high-Tcsuperconductivity. _Rev.

Mod. Phys._ 60, 585–600 (1988). Article  CAS  Google Scholar  * Zhang, L. et al. Giant polarization in super-tetragonal thin films through interphase strain. _Science_ 361, 494–497 (2018).

CAS  Google Scholar  * You, Y. -M. et al. An organic-inorganic perovskite ferroelectric with large piezoelectric response. _Science_ 357, 306–309 (2017). Article  CAS  Google Scholar  *

Akutagawa, T. et al. Ferroelectricity and polarity control in solid-state flip-flop supramolecular rotators. _Nat. Mater._ 8, 342 (2009). Article  CAS  Google Scholar  * Zhang, Y. et al.

Ferroelectricity induced by ordering of twisting motion in a molecular rotor. _J. Am. Chem. Soc._ 134, 11044–11049 (2012). Article  CAS  Google Scholar  * Xu, B. & Ren, S. Integrated

charge transfer in organic ferroelectrics for flexible multisensing materials. _Small_ 12, 4502–4507 (2016). Article  CAS  Google Scholar  * Ye, H. -Y. et al. Metal-free three-dimensional

perovskite ferroelectrics. _Science_ 361, 151–155 (2018). Article  CAS  Google Scholar  * Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. _Phys.

Rev. Lett._ 77, 3865–3868 (1996). Article  CAS  Google Scholar  * Grimme, S., Antony, J., Ehrlich, S. & Krieg, H. A consistent and accurate ab initio parametrization of density

functional dispersion correction (DFT-D) for the 94 elements H-Pu. _J. Chem. Phys._ 132, 154104 (2010). Article  Google Scholar  * Kresse, G. & Furthmüller, J. Efficient iterative

schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996). Article  CAS  Google Scholar  * Kresse, G. & Furthmüller, J.

Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. _Comput. Mater. Sci._ 6, 15–50 (1996). Article  CAS  Google Scholar  * Kresse,

G. & Hafner, J. Ab initio molecular dynamics for liquid metals. _Phys. Rev. B_ 47, 558–561 (1993). Article  CAS  Google Scholar  * Gong, X. et al. First-principles investigation of the

Raman spectroscopy of perovskite-like crystal K3B6O10Cl. _Comput. Mater. Sci._ 83, 86–91 (2014). Article  CAS  Google Scholar  * Han, H., Yin, G. & Wickramaratne, D. A first-principles

investigation of the electronic, elastic, piezoelectric and acoustic properties of K3B6O10Cl. _Comput. Mater. Sci._ 69, 81–86 (2013). Article  CAS  Google Scholar  * Wang, H. et al. Pressure

induced variation of second harmonic efficiency of K3B6O10Cl. _Appl. Phys. Lett._ 103, 101902 (2013). Article  Google Scholar  * Sakai, H. et al. Displacement-type ferroelectricity with

off-center magnetic ions in perovskite Sr_{1-x}Ba_{x}MnO_{3}. _Phys. Rev. Lett._ 107, 137601 (2011). Article  CAS  Google Scholar  * Giovannetti, G., Kumar, S., Ortix, C., Capone, M. &

van den Brink, J. Microscopic origin of large negative magnetoelectric coupling in Sr_{1/2}Ba_{1/2}MnO_{3}. _Phys. Rev. Lett._ 109, 107601 (2012). Article  Google Scholar  * Z-j, Wu et al.

Structures and elastic properties of superhard IrN2 and IrN3 from first principles. _Phys. Rev. B_ 76, 054115 (2007). Article  Google Scholar  * Chakarova-Käck, S. D., Schröder, E.,

Lundqvist, B. I. & Langreth, D. C. Application of van der Waals density functional to an extended system: Adsorption of benzene and naphthalene on graphite. _Phys. Rev. Lett._ 96, 146107

(2006). Article  Google Scholar  * Silvestrelli, P. L. Improvement in hydrogen bond description using van der Waals-corrected DFT: The case of small water clusters. _Chem. Phys. Lett._ 475,

285–288 (2009). Article  CAS  Google Scholar  * Dion, M., Rydberg, H., Schröder, E., Langreth, D. C. & Lundqvist, B. I. Van der Waals density functional for general geometries. _Phys.

Rev. Lett._ 92, 246401 (2004). Article  CAS  Google Scholar  * Kolb, B. & Thonhauser, T. van der Waals density functional study of energetic, structural, and vibrational properties of

small water clusters and ice I h. _Phys. Rev. B_ 84, 045116 (2011). Article  Google Scholar  * Baur, W. H. The geometry of polyhedral distortions. Predictive relationships for the phosphate

group. _Acta Crystallogr Sect. B: Struct. Sci._ 30, 1195–1215 (1974). Article  CAS  Google Scholar  * He, J., Borisevich, A., Kalinin, S., Pennycook, S. & Pantelides, S. Control of

octahedral tilts and magnetic properties of perovskite oxide heterostructures by substrate symmetry. _Phys. Rev. Lett._ 105, 227203 (2010). Article  Google Scholar  * Fuentes-Cabrera, M.,

Nicholson, D. M., Sumpter, B. G. & Widom, M. Electronic structure and properties of isoreticular metal-organic frameworks: The case of M-IRMOF1 (M = Zn, Cd, Be, Mg, and Ca). _J. Chem.

Phys._ 123, 124713 (2005). Article  Google Scholar  * Auld, B. A. _Acoustic Fields and Waves in Solids_ (Wiley, 1973), Vol. I, Chap. 8. * Yue, W. & Yi-Jian, J. Crystal orientation

dependence of piezoelectric properties in LiNbO3 and LiTaO3. _Opt. Mater._ 23, 403–408 (2003). Article  Google Scholar  * Bowen, C., Kim, H., Weaver, P. & Dunn, S. Piezoelectric and

ferroelectric materials and structures for energy harvesting applications. _Energy Environ. Sci._ 7, 25–44 (2014). Article  CAS  Google Scholar  * Crisler, D., Cupal, J. & Moore, A.

Dielectric, piezoelectric, and electromechanical coupling constants of zinc oxide crystals. _Proc. IEEE_ 56, 225–226 (1968). Article  CAS  Google Scholar  * Tokarev, E., Kobyakov, I.,

Kuz’mina, I., Lobachev, A. & Pado, G. Elastic, dielectric, and piezoelectric properties of zincite in the 4.2–800 K temperature range. _Sov. Phys. Solid State_ 17, 629–632 (1975). Google

Scholar  * Catti, M., Noel, Y. & Dovesi, R. Full piezoelectric tensors of wurtzite and zinc blende ZnO and ZnS by first-principles calculations. _J. Phys. Chem. Solids_ 64, 2183–2190

(2003). Article  CAS  Google Scholar  * Hayward, G., Bennett, J. & Hamilton, R. A theoretical study on the influence of some constituent material properties on the behavior of 1–3

connectivity composite transducers. _J. Acoust. Soc. Am._ 98, 2187–2196 (1995). Article  Google Scholar  * Goldschmidt, V. M. Die gesetze der krystallochemie. _Naturwissenschaften_ 14,

477–485 (1926). Article  CAS  Google Scholar  * Reaney, I. M., Colla, E. L. & Setter, N. Dielectric and structural characteristics of Ba-and Sr-based complex perovskites as a function of

tolerance factor. _Jpn. J. Appl. Phys._ 33, 3984 (1994). Article  CAS  Google Scholar  * Burger, S., Ehrenreich, M. & Kieslich, G. Tolerance factors of hybrid organic–inorganic

perovskites: recent improvements and current state of research. _J. Mater. Chem. A_ 6, 21785–21793 (2018). Article  CAS  Google Scholar  * Travis, W., Glover, E., Bronstein, H., Scanlon, D.

& Palgrave, R. On the application of the tolerance factor to inorganic and hybrid halide perovskites: a revised system. _Chem. Sci._ 7, 4548–4556 (2016). Article  CAS  Google Scholar  *

Kieslich, G., Sun, S. & Cheetham, A. K. Solid-state principles applied to organic–inorganic perovskites: new tricks for an old dog. _Chem. Sci._ 5, 4712–4715 (2014). Article  CAS  Google

Scholar  * Shannon, R.D. Revised effective ionic radii and systematic studies of interatomie distances in halides and chaleogenides. _Acta Crystallogr. Sect. A_ 32, 751–767 (1976). Article

  Google Scholar  * Hill, R. The elastic behaviour of a crystalline aggregate. _Proc. Phys. Soc. Sect. A_ 65, 349 (1952). Article  Google Scholar  * Yu, C. -F., Cheng, H. -C. & Chen, W.

-H. An Ab-initio study of structural, elastic, electronic and thermodynamic properties of triclinic Cu 7 In 3. _Mater. Chem. Phys._ 174, 70–80 (2016). Article  CAS  Google Scholar  * Ortiz,

A. U., Boutin, A., Fuchs, A. H. & Coudert, F. X. Anisotropic elastic properties of flexible metal-organic frameworks: how soft are soft porous crystals? _Phys. Rev. Lett._ 109, 195502

(2012). Article  Google Scholar  * Oganov, A. R. _Computer Simulation Studies of Minerals_. Ph.D. Thesis, University of London (2002). * Ross, N. L. & Angel, R. J. Compression of CaTiO3

and CaGeO3 perovskites. _Am. Mineral._ 84, 277–281 (1999). Article  CAS  Google Scholar  * Li, Z., Grimsditch, M., Foster, C. & Chan, S. -K. Dielectric and elastic properties of

ferroelectric materials at elevated temperature. _J. Phys. Chem. Solids_ 57, 1433–1438 (1996). Article  CAS  Google Scholar  * Piskunov, S., Heifets, E., Eglitis, R. & Borstel, G. Bulk

properties and electronic structure of SrTiO3, BaTiO3, PbTiO3 perovskites: an ab initio HF/DFT study. _Comput. Mater. Sci._ 29, 165–178 (2004). Article  CAS  Google Scholar  * Mahmoud, A.,

Erba, A., El-Kelany, K. E., Rérat, M. & Orlando, R. Low-temperature phase of BaTiO 3: Piezoelectric, dielectric, elastic, and photoelastic properties from ab initio simulations. _Phys.

Rev. B_ 89, 045103 (2014). Article  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953–17979 (1994). Article  Google Scholar  * Le Page, Y. & Saxe,

P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. _Phys. Rev. B_ 65, 104104 (2002). Article  Google Scholar  * Wu,

X., Vanderbilt, D. & Hamann, D. Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory. _Phys. Rev. B_ 72, 035105 (2005). Article 

Google Scholar  * Momma, K. & Izumi, F. VESTA 3for three-dimensional visualization of crystal, volumetric and morphology data. _J. Appl. Crystallogr_ 44, 1272–1276 (2011). Article  CAS 

Google Scholar  Download references ACKNOWLEDGEMENTS This work is supported by the National Natural Science Foundation of China (U1404111, 11504089, 61874160, 61675064, and 11404098), Young

Key Teacher of Henan Province (2016GGJS-059) and Collaborative Innovation Center of Nonferrous Metals of Henan Province. The crystal structure was drawn using the VESTA software.52 AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * School of Physics and Engineering, Henan University of Science and Technology, 471003, Luoyang, China Hui Wang, Huihui Liu, Zeyu Zhang, Zihan Liu, 

Zhenlong Lv, Tongwei Li, Weiwei Ju & Haisheng Li * Institute of Microelectronics of Chinese Academy of Sciences, 100029, Beijing, China Xiaowu Cai * School of Physical Science and

Technology, Shanghai Tech University, 201210, Shanghai, China Han Han Authors * Hui Wang View author publications You can also search for this author inPubMed Google Scholar * Huihui Liu

View author publications You can also search for this author inPubMed Google Scholar * Zeyu Zhang View author publications You can also search for this author inPubMed Google Scholar * Zihan

Liu View author publications You can also search for this author inPubMed Google Scholar * Zhenlong Lv View author publications You can also search for this author inPubMed Google Scholar *

Tongwei Li View author publications You can also search for this author inPubMed Google Scholar * Weiwei Ju View author publications You can also search for this author inPubMed Google

Scholar * Haisheng Li View author publications You can also search for this author inPubMed Google Scholar * Xiaowu Cai View author publications You can also search for this author inPubMed 

Google Scholar * Han Han View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.W., H.H.L., Z.Y.Z., and Z.H.L. did the PBE calculations, Z.L.L.,

T.W.L., and H.H. did the PBE + D3 calculations. W.W.J., H.S.L., and X.W.C. provided valuable comments and suggestions to the work. H.W. and H.H. wrote the paper. All authors have given

approval to the final version of the manuscript. CORRESPONDING AUTHORS Correspondence to Hui Wang or Han Han. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing

interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wang, H., Liu, H.,

Zhang, Z. _et al._ Large piezoelectric response in a family of metal-free perovskite ferroelectric compounds from first-principles calculations. _npj Comput Mater_ 5, 17 (2019).

https://doi.org/10.1038/s41524-019-0157-4 Download citation * Received: 31 August 2018 * Accepted: 22 January 2019 * Published: 06 February 2019 * DOI:

https://doi.org/10.1038/s41524-019-0157-4 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative