Reader TTS

ABSTRACT The negatively charged silicon vacancy center (\({{\rm{V}}}_{{\rm{Si}}}^{-}\)) in silicon carbide (SiC) is an emerging color center for quantum technology covering quantum sensing,

communication, and computing. Yet, limited information currently available on the internal spin-optical dynamics of these color centers prevents us from achieving the optimal operation

conditions and reaching the maximum performance especially when integrated within quantum photonics. Here, we establish all the relevant intrinsic spin dynamics of the

\({{\rm{V}}}_{{\rm{Si}}}^{-}\) center at cubic lattice site (V2) in 4H-SiC by an in-depth electronic fine structure modeling including the intersystem-crossing and deshelving mechanisms.

With carefully designed spin-dependent measurements, we obtain all the previously unknown spin-selective radiative and non-radiative decay rates. To showcase the relevance of our work for

integrated quantum photonics, we use the obtained rates to propose a realistic implementation of time-bin entangled multi-photon GHZ and cluster state generation. We find that up to

three-photon GHZ or cluster states are readily within reach using the existing nanophotonic cavity technology. SIMILAR CONTENT BEING VIEWED BY OTHERS FABRICATION AND NANOPHOTONIC WAVEGUIDE

INTEGRATION OF SILICON CARBIDE COLOUR CENTRES WITH PRESERVED SPIN-OPTICAL COHERENCE Article 18 November 2021 INVERTED FINE STRUCTURE OF A 6H-SIC QUBIT ENABLING ROBUST SPIN-PHOTON INTERFACE

Article Open access 03 March 2022 ROBUST SINGLE MODIFIED DIVACANCY COLOR CENTERS IN 4H-SIC UNDER RESONANT EXCITATION Article Open access 22 November 2024 INTRODUCTION Solid-state spin qubits

based on color centers in wide bandgap semiconductors are one of the leading platforms for quantum networks, information processing, and sensing1,2,3,4 owing to their robust spin-optical

properties and long coherence times. Among many available host materials5,6,7, silicon carbide (SiC) particularly stands out as a wafer-scalable material with well-established isotopic

engineering and compatibility with today’s complementary metal-oxide-semiconductor (CMOS) microfabrication technology providing a path towards scalable systems. Rapid progress with spin

qubits in SiC has already been made including the milestone demonstrations of millisecond spin coherence times at room temperature8,9, high-fidelity spin and optical control10, coherent

spin-photon interfaces11, entanglement with nuclear spin registers12, and single-shot charge readout13. Capitalizing on the SiC’s material advantages, steps towards scalability have also

been implemented through successful integration of negatively charged silicon vacancy color centers (\({{\rm{V}}}_{{\rm{Si}}}^{-}\)) into nanophotonic waveguides14 and resonators15,16,17,

the latter one being compatible with SiC-on-insulator processing18. These proof-of-concept demonstrations identify the cubic lattice site \({{\rm{V}}}_{{\rm{Si}}}^{-}\), i.e. V2 in 4H-SiC as

a strong contender for quantum applications based on a dense integration of multiple color centers on one chip. Further progress towards fully scalable integrated solutions with V2 is

necessitated by a complete understanding of its intrinsic spin-optical dynamics to guide the engineering efforts of cavity-emitter coupling and optimization of spin and optical properties.

It will also provide the critical insights and metrics necessary for developing realistic quantum network applications. In this paper, we focus on the V2 center in 4H-SiC occupying the cubic

lattice site having a much larger zero-field splitting8 (ZFS) in the ground state compared to the hexagonal-site V1 center10. This larger ZFS leads to a much faster ground-state spin

manipulation and higher state fidelities19. We reveal the comprehensive internal spin dynamics of the V2 center by theoretical characterization of its electronic structure. The theory is

confirmed by our experimental investigations, which include the measurements of spin-selective excited state (ES) lifetimes, ground state spin initialization via resonant and off-resonant

laser excitation, as well as probing the intricate dynamics within the metastable state (MS) manifolds via spin manipulation combined with a delayed pulse measurement. In this way, we

determine all the spin-dependent radiative and non-radiative transition rates and identify the intersystem crossing (ISC) mechanism which all play a crucial role in defining realistic

protocols for scalable quantum network applications. To showcase this, we develop a protocol for generating time-bin entangled multi-photon Greenberger-Horne-Zeilinger20 (GHZ) and cluster

states21, which are particularly important for quantum network applications, one-way quantum computation, and quantum repeaters. Using the involved intrinsic transition rates and ISC

mechanism, we provide estimates for quantum efficiencies, state fidelities, optimal pulse timings, and minimum requirements for a cavity enhancement of radiative lifetimes. The approaches

and insights developed here are also directly applicable to other color centers and their benchmarking for specific applications. RESULTS ELECTRONIC FINE STRUCTURE OF

\({{\RM{V}}}_{{\RM{SI}}}^{-}\) IN 4H-SIC The crystal structure of 4H-SiC allows for two nonequivalent lattice sites, so-called hexagonal (h) and cubic (k) sites, to be occupied by the deep

center \({{\rm{V}}}_{{\rm{Si}}}^{-}\) defect. Defects belonging to the h- and k-sites, referred to as the V1 and V2 centers, have distinct optical resonant excitation signatures at

zero-phonon line (ZPL) wavelengths of 862 nm and 916 nm, respectively. Five active electrons present in V1 and V2, originating from the four sp3 dangling bonds surrounding the vacancy and an

additional captured negative charge, result with optically active ground and excited states in a Kramer’s degenerate _S_ = 3/2 spin quartet configuration. Both V1 and V2 have a local

symmetry that belongs to the C3v double point group that is only slightly distorted from the cubic Td symmetry. In the case of V2, this distortion is stronger because of the additional next

nearest neighbor silicon atom present along the c-axis for k-sites. As we will show in this work, this leads to a completely different spin-optical dynamics of the V2 center compared to the

formerly studied V1 center22. To investigate the dynamics of the V2 center (from now on dubbed as \({{\rm{V}}}_{{\rm{Si}}}^{-}\) center), we use the group theoretical framework, developed by

Soykal et al. 23, based on multi-particle symmetry adapted total wavefunctions built from single-electron molecular orbitals (MOs) and linear combinations of localized many body sp3

orbitals. Combining the theory and our experimental measurements, we reveal all the spin-dependent radiative and non-radiative transition rates, and as a result the intrinsic optical and

spin dynamics of \({{\rm{V}}}_{{\rm{Si}}}^{-}\). Our results corroborate a complete picture of all the metastable-state doublets involved in the ISC and spin polarization of this defect with

their relevant coupling mechanisms (spin-orbit, dynamic pseudo-Jahn Teller, and optical deshelving) as explained in the following subsections. Although the possible involvement of

higher-lying doublets within the ISC was previously pointed out by Dong et al.24, some of the crucial ISC doublet states were either missing or obtained incorrectly there, e.g. missing an

extra _uve_ doublet or not satisfying the orthonormality condition for the presented one. Coupled with lack of prior experimental data, critical mechanisms such as pseudo-Jahn Teller effect

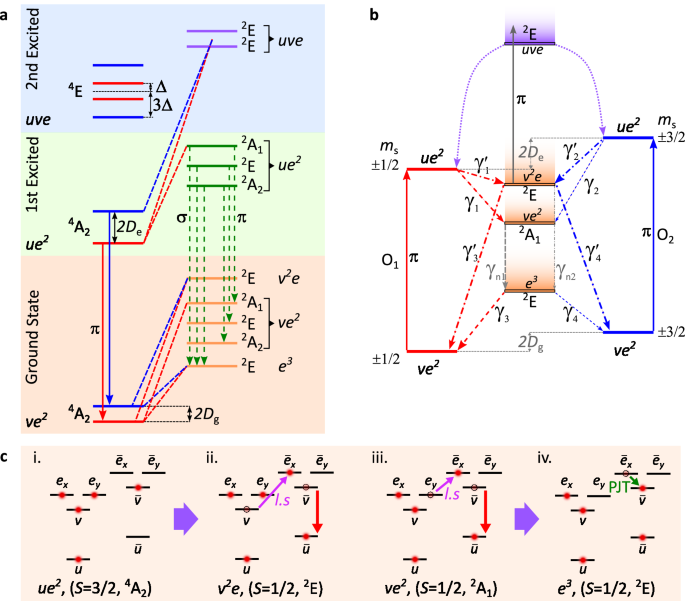
and involvement of a deshelving state were also not identified leaving the ISC still an open question. The comprehensive \({{\rm{V}}}_{{\rm{Si}}}^{-}\) electronic fine structure is shown in

Fig. 1a, in terms of MOs obtained by group theoretical analysis and considerations of many-body spin-orbit, spin-spin, and exchange interactions (see Supplementary Note 2). The ground state

(GS) manifold contains a spin-quartet state in an orbital-singlet (4A2 : _ve_2) configuration and five metastable spin-doublet states. These doublets consist of two orbital-singlet (2A1, 2A2

: _ve_2) and three orbital-doublet (2E : _ve_2_, e_3_, v_2_e_) configurations (see ref. 23 and Supplementary Note 2). The first excited state manifold differs from the ground state solely

in the _u_ orbital, replacing _v_ (_ve_2→ _ue_2). This leads to a spin-quartet orbital-singlet state (4A2 : _ue_2) and three metastable spin-doublet states. These doublets consist of two

orbital-singlets (2A1 : _ue_2, 2A2 : _ue_2) and an orbital-doublet (2E : _ue_2) configurations. It has been shown that the charge distribution localized on the nearest neighbor basal plane

carbon atoms has an opposite parity for the _u_ and _v_ MOs, making the transition dipole moment (\({\mu}_{{ve}^{2} \rightarrow {ue}^{2}}\) less sensitive to fluctuations in non-axial local

electric field and strain, even though \({{\rm{V}}}_{{\rm{Si}}}^{-}\) defect lacks an inversion symmetry25. This explains the experimentally observed high spectral stability of

\({{\rm{V}}}_{{\rm{Si}}}^{-}\) center during a continuous resonant optical excitation14,16. The second excited state manifold includes another optically active spin-quartet orbital-doublet

(4E : _uve_), which is split by the spin-orbit coupling, as well as two metastable spin-doublet orbital-doublet states (2E : _uve_). The symmetry-allowed spin-orbit coupling channels are

indicated in Fig. 1a (dashed lines and arrows). Based on the described fine structure and the allowed coupling channels, we develop a simplified and a fully equivalent energy level model of

the \({{\rm{V}}}_{{\rm{Si}}}^{-}\) center as shown in Fig. 1b. It consists of Kramer’s degenerate ground and excited states for the spin subspaces _m_s = ±1_/_2 and _m_s = ±3_/_2, and three

effective metastable states, which can be further reduced to two as we show in the analysis below. The spin-conserving optical transitions between ground and excited states are denoted by O1

and O2 for each spin subspace whereas the additional radiative and intersystem-crossing (ISC) rates are denoted by _γ__i_. In this work, we use resonant and off-resonant optical excitation

methods to extract all the transition rates shown in Fig. 1b, and we will show that the results are in excellent agreement with our theoretical calculations. The intrinsic spin dynamics of

the \({{\rm{V}}}_{{\rm{Si}}}^{-}\) defect under optical illumination is governed by the radiative transitions between states of the same spin multiplicity as well as nonradiative ISCs

between states of different spin multiplicity. In the case of optical excitation of the first excited state, the ISC is established by two processes involving: * i. Transitions from the

optical (4A2 : _ue_2) first excited spin-quartet state to energetically higher metastable spin-doublet states (2E : _v_2_e_; 2A1 : _ve_2). * ii. Transitions from the metastable spin-doublet

states (2E : _e_3_,v_2_e_) to the ground spin-quartet (4A2 : _ve_2) state. Both processes are mediated by a combination of spin-orbit (spin-lowering/raising) and electron-phonon

(spin-conserving) interactions. The ISC mechanisms involved in these transitions can be explained intuitively using the simpler MO picture as shown in Fig. 1c. ISC MECHANISM The upper ISC

mechanism is governed by the _γ_1,2 and \({\gamma }_{\mathrm{1,2}}^{{\prime} }\) rates (ES to MSs) in Fig. 1b. It consists of transitions from the 4A2 : _ue_2 spin quartet state to the 2E :

_v_2_e_ and 2A1 : _ve_2 spin-doublets, being assisted by both the spin-orbit coupling and the electron-phonon interaction. Consider the system to be initially in the excited state _ue_2

spin-quartet configuration, as shown in the inset (i) of Fig. 1c. From here, and as shown in the inset (ii) of Fig. 1c, the spin-orbit coupling (_α__y__l__y__s__y_) can promote an electron

from the _v_ orbital to the \({\bar{e}}_{x}\) orbital. This is followed by a fast spin-conserving decay of a second electron from the \(\bar{v}\) orbital to the \(\bar{u}\) orbital via

either a photon emission or a phonon relaxation process. This then leads to the _v_2_e_ spin-doublet configuration. The inset (iii) of Fig. 1c shows an alternative pathway from the

configuration in (i). Here, the spin-orbit coupling (_α__z__l__z__s__z_) can promote an electron from the _e__y_ to the \({\bar{e}}_{x}\) orbital. Again, this is followed by the \(\bar{v}\to

\bar{u}\) decay, resulting in the _ve_2 spin-doublet. In fact, due to the stronger spin-orbit coupling along the c-axis (_α__z_ > _α__x,y_), the latter process (iii) is expected to be

faster than (ii), which will be confirmed by our experimental investigations. As shown in the inset (iv) in Fig. 1c, we must also consider that the _ve_2 and the _e_3 spin-doublet states can

be vibronically coupled together by the _e_-symmetry acoustic phonons (2A1 × _e_ × 2E) via the pseudo-Jahn Teller (PJT) effect. This allows the _ve_2 spin-doublet of (iii) to transition

into the _e_3 spin-doublet state at a relatively fast dynamic relaxation rate (\(\gamma_{n1} \, \gg \, \gamma_{1,2}\)) which redistributes most of the population into the _e_3 spin-doublet

during an optical excitation cycle. DESHELVING MECHANISM Subsequently, the non-radiative transition of the _e_3 spin-doublet state to the ground _ve_2 spin-quartet state forms the basis of

the lower ISC mechanism represented by the effective _γ_3,4 rates (MS to GS). In the MS manifold, the _ve_2 doublets experience ultra-fast relaxation to the _e_3 doublets (_γ_n1), which is

why we can combine them into a single effective spin-doublet state. On the other hand, the _v_2_e_ state lacks a similar fast relaxation path (\({\gamma }_{{\rm{n}}2}\sim 0\)), thus

resulting in low non-radiative decay rates \({\gamma }_{\mathrm{3,4}}^{{\prime} }\) to the ground state. Interestingly, the rather long lifetime of the _v_2_e_ state can result in a sizeable

optical excitation rate into the higher-lying _uve_ spin-doublet state (Fig. 1b). In this previously unknown deshelving process, an electron is promoted from the \(\bar{u}\) to the

\(\bar{v}\) orbital (solid gray line in Fig. 1b). Here, the optical excitation is required to have the same polarization (π) and similar energy as the O1 and O2 transitions (only differing

by the electron exchange correlations). The cycle is then completed by a spin-orbit mediated non-radiative transition from the _uve_ spin-doublet to the _ue_2 first excited state (purple

dashed arrows in Fig. 1b). This mechanism is expected to manifest itself as a laser power-dependent \({\gamma }_{\mathrm{3,4}}^{{\prime} }\) rates during a continuous resonant or

off-resonant optical excitation of the \({{\rm{V}}}_{{\rm{Si}}}^{-}\) defect further evidenced by our experimental observations. The effective rate model for V2 is summarized into a

six-level rate model (see Supplementary Note 1) as: 1) the metastable-state doublets _ve_2 and lowest _e_3 are combined into one level due to ultrafast relaxation (\({\gamma

}_{{\rm{n}}1}\)), and 2) the power-dependent deshelving mechanism is represented by the power-dependent decay rates \({\gamma }_{\mathrm{3,4}}^{{\prime} }\). Our theoretical calculations are

based on this effective six levels to model the experimental data for inferring all the relevant rates. EXPERIMENTAL DETERMINATION OF THE SPIN-DEPENDENT EXCITED-STATE LIFETIMES Firstly, we

measure the spin-dependent excited-state lifetimes using the experimental sequence depicted in Fig. 2a (see Methods and ref. 22). A “repump” laser pulse is used to ensure that the

\({{\rm{V}}}_{{\rm{Si}}}^{-}\) center is in the desired negative charge state. This is followed by a sub-lifetime short (1.5 ns) laser pulse at 916.5 nm, resonant with either the O1 or O2

transition. The fluorescence decay signal is recorded and subsequently fitted using a single exponential function as shown in Fig. 2b. We determine the excited-state lifetimes of bulk V2

centers as 6.1 ns and 11.3 ns for the O1 and O2 transitions, respectively. Here, we note that the O2 lifetime is almost twice as long as O1, which is in stark contrast with the two nearly

identical spin-dependent excited state lifetimes of V1 center in 4H-SiC22. This indicates the V2 center has a much slower intersystem crossing for the ±3/2 spin sublevels associated with the

O2 transition (compared to the spin ±1/2 sublevels belonging to the O1 optical transition). This also implies a significantly higher quantum efficiency for the O2 transition which has been

experimentally observed in a recent work with the V2 centers integrated into nanophotonic resonators16. PROBING THE METASTABLE-STATE DYNAMICS OF THE V2 CENTER We now investigate the

predominant decay processes out of metastable states. This requires pumping of the system into the MSs followed by the determination of subsequent spin populations \({p}_{1/2}\) and

\({p}_{3/2}\) within the spin subspaces of \({m}_{{\rm{s}}}=\pm 1/2\) and \({m}_{{\rm{s}}}=\pm 3/2\), respectively. For these studies, we take advantage of the following three key features:

First, it is known that a prolonged off-resonant excitation of \({{\rm{V}}}_{{\rm{Si}}}^{-}\) center pumps the system into the MS which is followed by a partial, non-complete spin

polarization. It is assumed that the \({m}_{{\rm{s}}}=\pm 1/2\) subspace shows a slightly higher population compared to the \({m}_{{\rm{s}}}=\pm 3/2\) subspace26. Second, a prolonged

resonant excitation along the O2 or O1 transitions can be used to achieve a (nearly) complete polarization into the \({m}_{{\rm{s}}}=\pm 1/2\) or \({m}_{{\rm{s}}}=\pm 3/2\) subspaces,

respectively10,22. Third, the resonant excitation permits us to selectively read out the spin populations \({p}_{1/2}\) and \({p}_{3/2}\) in the subspaces \({m}_{{\rm{s}}}=\pm 1/2\) and

\({m}_{{\rm{s}}}=\pm 3/2.\) It is not straightforward to infer the relative population or population contrast of the ground states via the fluorescence intensities under the O1 and O2

excitation as they depend on the ISC rates and quantum efficiency of each spin-dependent transition. For this reason, we then measure spin Rabi oscillations and determine the ground-state

population contrast for probing the metastable-state dynamics. The related experimental sequence is shown in Fig. 3a. The sequence starts by predominantly initializing the system into the

\({m}_{{\rm{s}}}=\pm 1/2\) (\({m}_{{\rm{s}}}=\pm 3/2)\) spin subspace using ~0.5 µs long resonant excitation along the O2 (O1) transition. Subsequently, an off-resonant laser pulse, with

varying duration of _T_repump and fixed power of 30 µW, is applied to increase the population in the MS, after which we allow the system to relax back to the ground states. To determine the

absolute spin populations \({p}_{1/2}\) and \({p}_{3/2}\), we then perform spin-Rabi oscillations using a microwave drive at a frequency of 70 MHz, corresponding to the ground state

splitting between the \({m}_{{\rm{s}}}=\pm 1/2\) and \({m}_{{\rm{s}}}=\pm 3/2\) subspaces. Finally, the spin population is read out by integrating the fluorescence intensity during a 0.5 µs

short resonant laser pulse along the O2 (O1) transition. We note that the short readout pulse duration ensures that we exclude any complex dynamics stemming from ISCs, so that the

fluorescence intensity signal is proportional to the ground state population. Overall, this sequence allows us to determine the ground state population contrast \(\Delta

p=(|{p}_{1/2}-{p}_{3/2}|)/({p}_{1/2}+{p}_{3/2})\) as a function of the off-resonant laser pulse duration _T_repump (for more details, see Supplementary Note 3). The bottom inset of Fig. 3a

shows the obtained experimental data. For short times of _T_repump, the system has not yet reached an equilibrium (partial incomplete spin polarization into the \({m}_{{\rm{s}}}=\pm 1/2\)

subspace26). This is witnessed by a strong population contrast in both cases after initialization into the subspaces of either \({m}_{{\rm{s}}}=\pm 1/2\) (blue) or \({m}_{{\rm{s}}}=\pm 3/2\)

(red). For _T_repump >40 µs, the population contrast reaches a steady state value of \(\Delta p \sim 0.14\). Crucially, the behavior of the population contrast for both initializations

is different. After initialization into \({m}_{{\rm{s}}}=\pm 1/2\), we find a monotonic decay of Δ_p_. In contrast for initialization into \({m}_{{\rm{s}}}=\pm 3/2\), we observe a decay to

\(\Delta p \sim 0\) at _T_repump ~10 µs followed by an increase to the steady state value \(\Delta p \sim 0.14.\) This is explained by the initial population \({p}_{3/2} \sim 1\) dropping to

\({p}_{3/2} \sim 0.5\) after \({T}^{\text{repump}} \sim 10\) µs, and further decreasing to \({p}_{3/2} \sim 0.43\) for \({T}^{\text{repump}} > 40\) µs. In other words, our experimental

results unambiguously determine that the \({m}_{{\rm{s}}}=\pm 1/2\) subspace is preferably populated from the MSs with a ratio of 0.57/0.43 at an off-resonant laser power of 30 µW. It is

important to mention that optical re-excitation i.e. deshelving processes within the MSs are allowed by the selection rules (see Fig. 1b) and have been experimentally observed27,28.

Re-excitation can drastically alter the spin population dynamics and as we show in the Supplementary Note 3 we can achieve a ground state population ratio of 0.65/0.35 for an off-resonant

laser power of 4 mW. Having already established that the system reaches a steady state at 30 µW off-resonant pump power after \({T}^{\text{repump}} \sim 40\) µs, we now proceed to the

high-fidelity spin initialization using a resonant excitation along the O1 (O2) transition. The related experimental sequence is shown in Fig. 3b (upper panel). An off-resonant laser pulse

of 40 µs duration and 30 µW power establishes a steady state (0.57/0.43 ground state populations). Thereafter, a resonant laser pulse of duration _T_ and power 6 nW initiates the

high-fidelity spin pumping. The absolute ground state spin populations are read out as before (spin Rabi oscillations, followed by a 0.5 µs spin-selective resonant laser excitation). The

experimental results are shown in Fig. 3b (lower inset). For _T_ > 20 µs, we reach high initialization fidelities of 95(1)% and 93(1)% into the spin subspaces \({m}_{{\rm{s}}}=\pm 1/2\)

(blue) or \({m}_{{\rm{s}}}=\pm 3/2\) (red) under O2 and O1 optical pumping, respectively. To further investigate the decay rates from the metastable (MS) states to the ground states (see

Fig. 1b), we develop a delayed measurement scheme, as depicted in Fig. 3c. We use a 4 µs long off-resonant laser excitation pulse at 4 mW power, to trap most of the spin population in the

MSs at the end of the pulse. This is due to the considerably longer lifetimes of the MSs compared to the excited-state lifetimes and the optical excitation rates. We then capture the MS

depopulation dynamics by measuring the time-dependent increase of the ground state populations. To this end, we permit the system to relax to the ground state for a duration of _T_Delay

before starting to integrate the fluorescence emission for 0.1 µs during a resonant excitation along the O1 and O2 transitions. We note that these measurements capture all the rates in and

out of the MS states29 which are populated by the incoming ISC rates (\({\gamma }_{\mathrm{1,2}},{\gamma }_{\mathrm{1,2}}^{{\prime} }\)) and depopulated by the outgoing ones (\({\gamma

}_{\mathrm{3,4}},{\gamma }_{\mathrm{3,4}}^{{\prime} }\)). The related experimental data is shown in Fig. 3c (bottom inset). The graph also includes the simulated curves using the ISC model

and rates given in Table 1 showing an excellent agreement between the experiment and theory. We note that these rates have been inferred through the MS dynamics probed until here and

subsequent power-dependent resonant-excitation measurements which are discussed in the next section. POWER-DEPENDENT RESONANT-EXCITATION SPIN INITIALIZATION MEASUREMENTS To obtain a

comprehensive understanding of the spin initialization process through resonant excitation, we use the resonant laser power as an additional probing parameter ranging from 6 nW to 20 nW. We

limit the maximum power to 20 nW to avoid excessive photo-ionization30, as well as power broadening, which would result with the loss of spin selectivity31. As depicted in Fig. 4a, the

measurement sequence consists of an off-resonant excitation pulse (32 µW, 40 µs) to initialize the \({{\rm{V}}}_{{\rm{Si}}}^{-}\) center into the negatively charged state and to initialize

the ground state into slightly unbalanced spin populations (see Fig. 3a). Then, we selectively depopulate the spin subspaces \({m}_{{\rm{s}}}=\pm 1/2\) or \({m}_{{\rm{s}}}=\pm 3/2\) through

continued resonant excitation along the O1 (or O2) optical transition while recording the fluorescence intensity for 40 µs. At all power levels, 40 µs resonant excitation is sufficiently

long to completely depopulate the respective spin sublevels, as witnessed by the fluorescence signals reaching the noise level of the single-photon detectors. As shown in Fig. 4b, the

time-dependent fluorescence intensity shows a tail that extends over to several microseconds. This indicates the involvement of a long-lived metastable state in the ISC, which is later

corroborated by our rate results (see Table 1). The state initialization fidelity extracted from the resonant optical pumping measurement reaches \(\sim 99.5\left(1\right) \%\) which is

higher than the value inferred from the spin Rabi oscillation which provides a lower bound of the state initialization fidelity. The lower fidelity in the latter case is caused by a small

residual magnetic field originating from the magnetization of the instruments mixing the ground state spin sublevels and it can be further improved by applying a sufficiently large external

magnetic field10,11. We now build a parameter optimization and fine-tuning algorithm that can be carried out over the density matrix master equation of the spin selective ISC model shown in

Fig. 1b, constrained only by the measured excited state lifetimes (see Methods). The time dependent fluorescence decay data at all four powers and the delayed pulse measurement data are all

simultaneously fitted using this algorithm. The resulting fit curves for the fluorescence decays are presented in Fig. 4b, showing excellent agreement with the experimental data. Individual

analysis of the resonant initialization and delayed pulse measurement leads to a differing number of metastable states. Our ISC model presented in Fig. 1b leads to an excellent agreement

with both measurements in Figs. 3 and 4, and involves a minimum number of metastable states for accurately describing the experimental data. The resulting transition rates are summarized in

Table 1. In accordance with the model in Fig. 1b, we find two effective metastable states playing a significant role in the ISC. The first metastable state (MS1) consists of the _ve_2 and

_e_3 spin-doublet states in which the fast dynamic relaxation (\({\gamma }_{{\rm{n}}1}\,\gg\, {\gamma }_{i},{\gamma }_{i}^{{\prime} }\)) of _ve_2 onto _e_3 is captured within. The second

effective metastable state (MS2) is formed from the _v_2_e_ spin-doublet state. Due to the deshelving of _v_2_e_ spin doublet to _uve_ spin doublet under optical excitation (see Fig. 1b),

the MS2 lifetime shows a significant power dependence during resonant excitation measurements. Using the deshelving model and taking 20 nW as a reference power, from each of the remaining

fit curves we theoretically infer the rest of the resonant excitation powers. The calculated powers are well within the experimental error tolerances showing excellent agreement (see Table

1) across all powers and providing further evidence of the deshelving mechanism. At this point we highlight key differences between the V1 and V2 centers in 4H-SiC. In our previous work, we

showed that V1 center has a metastable state with ∼200 ns lifetime22. This is very similar to the MS1 lifetime of the V2 center, as we have shown in this work. However, the V2 center shows

an additional long-lived MS2 metastable state (up to ∼3 µs at low excitation powers), for which no such evidence was observed for V1. We explain this difference by the PJT effect which

results in a strong vibronic mixing between the MS1 (_ve_2) and MS2 (_v_2_e_) states. For the V1 center with near-Td symmetry, this effectively results in a single metastable state due to

the increased degeneracy between the _v_ and _e_ MOs. On the other hand, for V2 centers, such degeneracy is removed by the much more distorted local symmetry (C3v) along the c-axis32,

suppressing any mixing. The weaker PJT effect for V2 centers is additionally confirmed by our recent work, which showed that V2 centers maintain narrow optical linewidths at significantly

higher temperatures compared to V1 centers32. The very long lifetime of MS2 also affects the behavior of V2 color centers under off-resonant excitation. Especially at high laser powers,

Stokes excitation can lead to another depletion channel for MS2 which eventually reduces the effective lifetime of the entire metastable state manifold to the lifetime of the MS1. This

behavior is experimentally corroborated by our high-repump-power results in Fig. 3c, as well as previous room-temperature investigations27,28. DISCUSSION From our measured rates for V2

centers in 4H-SiC, the higher quantum efficiency of the O2 transition with spin \(|{m}_{{\rm{s}}}|=1/2\) leads to a higher cooperativity (see Supplementary Note 4) when integrated in

nanophotonic resonators, which has been recently observed16. Here, we develop protocols for the generation of time-bin entangled multi-photon states from a single V2 center that can take

advantage of this high quantum efficiency of the O2 transition. We perform a detailed analysis of our protocols and consider multiple sources of imperfections including both spin conserving

(i.e., excited-state phonon scattering, imperfect excitation) and spin-flip (due to ISC mechanism) errors. Two ground-state spins \(|{{\rm{g}}}_{1}\rangle =|-1/2\rangle\) and

\(|{{\rm{g}}}_{2}\rangle =|-3/2\rangle\) are chosen as entanglers for the Greenberger-Horne-Zeilinger (GHZ) and one-dimensional cluster states. Our protocol is adapted from a similar concept

initially developed for quantum dots33 and consists of periodic optical drive of O2 and coherent microwave control of ground-state spins. The Kramer’s degenerate ground-state spins are

further split into four sublevels (see Fig. 5a) by applying a sufficiently large magnetic field (e.g., _B_ = 5 mT) for longer spin coherence time34. The entire protocol shown in Fig. 5b

involves the following steps: * i. The ground state spin is initialized to \({|{\rm{g}}}_{1},0\rangle +{|{\rm{g}}}_{2},0\rangle\) (normalization omitted w.l.o.g.) by resonant optical pumping

of O1 transition during a continuous microwave driving (IMW) of the spin \(|+3/2\rangle \leftrightarrow |+1/2\rangle\) transition followed by a microwave π/2 pulse

(\({\text{S}}_{\text{MW}}^{{\rm{\pi }}/2}\)) resonant with \(|-3/2\rangle \leftrightarrow |-1/2\rangle\). * ii. An optical π pulse resonantly excites the O2 transition resulting with the

spontaneous emission of the first ZPL photon into an early time bin: \({|{\rm{g}}}_{1},0\rangle +{|{\rm{g}}}_{2},{1}_{{\rm{E}}}\rangle\). * iii. The spin states are swapped via

\({\text{S}}_{\text{MW}}^{{\rm{\pi }}}\) pulse: \({|{\rm{g}}}_{2},0\rangle +{|{\rm{g}}}_{1},{1}_{{\rm{E}}}\rangle .\) * iv. Upon resonant excitation of O2 with a second _π_ pulse, another

photon is emitted into a late time bin: \({|{\rm{g}}}_{2},{1}_{{\rm{L}}}\rangle +{|{\rm{g}}}_{1},{1}_{{\rm{E}}}\rangle\). * v. For a GHZ state generation, a final

\({\rm{R}}={\text{S}}_{\text{MW}}^{{\rm{\pi }}/2}\) pulse (i.e., X-gate) is applied resulting with \({|{\rm{g}}}_{1},{1}_{{\rm{L}}}\rangle +{|{\rm{g}}}_{2},{1}_{{\rm{E}}}\rangle\).

Similarly, for a cluster state generation, the Pauli-X gate can be replaced by a Hadamard gate (\(\text{R}=\text{H}=\text{X}{\text{Y}}^{1/2}\)) resulting with a generator \({C}^{\dagger

}=|{{\rm{g}}}_{+}\rangle \langle {{\rm{g}}}_{2}|{a}_{\text{E}}^{\dagger }+|{{\rm{g}}}_{-}\rangle \langle {{\rm{g}}}_{1}|{a}_{\text{L}}^{\dagger }\) for each period with \(|{{\rm{g}}}_{\pm

}\rangle =(|{{\rm{g}}}_{1}\rangle \pm |{{\rm{g}}}_{2}\rangle )/\sqrt{2}\). By repeating one period (from ii to v) of this protocol _N_ times we obtain an _N_-photon GHZ state or a cluster

state depending on the final gate operation. The dephasing of the excited states for V2 centers induced by acoustic phonons was shown to be negligible by the preservation of narrow PLE

linewidths up to 20 K32. Therefore, the fidelity related to phonon-induced pure dephasing, defined33 as \({F}_{{\rm{p}}}^{{\rm{GHZ}},{\rm{C}}}=1-N{\gamma }_{{\rm{d}}}/({\gamma

}_{{\rm{r}}}+2{\gamma }_{{\rm{d}}})\), is close to 1 with \({\gamma}_{{\rm{d}}} \, \ll \, {\gamma}_{{\rm{r}}}\). We also consider excitation errors in the resonant driving pulses that induce

undesired stimulated photon emissions (weak, long pulse) and detuned O1 transition (strong, short pulse) given33 as \({F}_{{\rm{ex}}}=1-N\left(\frac{\sqrt{3}\pi }{8}\right){\gamma

}_{{\rm{r}}}/\Delta\). With our measured radiative decay rate and ∼1 GHz separation between O1 and O2 transitions, the pulse timing for a square π-pulse optimized upon 2π-rotation of the

detuned transition is found to be 0.9 ns for a three-photon GHZ/cluster state resulting in an excitation fidelity of 74.3%. The fidelity of the GHZ and cluster states with branching errors

(emission into phonon sideband and ISC) are the same for the protocol shown in Fig. 5 and given as \({{F}_{\text{br}}}^{{\rm{GHZ}},{\rm{C}}}={\left({P}_{{{\rm{O}}}_{2}}\right)}^{N}\)

conditioned upon a successful detection without any post-processing. \({P}_{{{\rm{O}}}_{2}}\) is the ZPL emission probability for the O2 radiative transition and defined as \((P\alpha

{\gamma }_{{\rm{r}}})/(\left(1-\alpha \right){\gamma }_{{\rm{r}}}+P\alpha {\gamma }_{{\rm{r}}}+{\gamma }_{2}+{\gamma }_{2}^{{\prime} })\) in terms of Debye-Waller factor \(\alpha \sim 9

\%\)32, Purcell factor _P_, and the rates inferred in Table 1. We find \({{F}_{\text{br}}}^{{\rm{GHZ}},{\rm{C}}}=0.06\) without any cavity Purcell enhancement with the above optimized pulse

timing. The cavity enhancement of radiative lifetime improves \({F}_{{\rm{p}}}^{{\rm{GHZ}},{\rm{C}}}\) and \({F}_{{\rm{br}}}^{{\rm{GHZ}},{\rm{C}}}\), but it degrades _F_ex slightly as the

excited state radiative lifetime is modified as \({\gamma }_{{\rm{r}}}\to \left(1-\alpha \right){\gamma }_{{\rm{r}}}+P\alpha {\gamma }_{{\rm{r}}}\). To maximize the overall fidelity defined

as \({F}_{{\rm{t}}}={F}_{{\rm{p}}}{F}_{{\rm{ex}}}{F}_{{\rm{br}}}\), we calculate the optimized Purcell factors for each state size as shown in Fig. 5c. The primary limitation to the total

fidelities shown here comes from the competition between the excitation and branching ratio errors as _F_br increases while _F_ex decreases with larger Purcell factors. To reach a total

fidelity of 50%, GHZ or cluster states of maximum three photons are feasible. We calculate the minimum required Purcell factors to reach _F_t = 50% (Fig. 5d) for various state sizes

compatible with existing nanophotonic resonators15,16,35. Photon states of larger size (>three photons) can be achieved by increasing the excited-state ZFS (~∆) via applied strain

allowing for much larger Purcell enhancements to be applied36. In comparison to the quantum dot platform where the linear cluster state has been realized21, the V2 centers additionally

provide excellent quantum memories based on electron and nuclear spins8,10,14,37. Thus, the system is in principle capable of connecting quantum memories with multi-photon states and

promising a loss-tolerant demonstrator which requires one emitter, two memories and six photons38. In summary, we have established the complete electronic fine structure and intrinsic spin

dynamics of the V2 silicon vacancy centers in 4H-SiC unraveling all the previously unknown spin-dependent radiative and non-radiative decay rates, ISC, and deshelving mechanisms. The

mechanisms identified here successfully explain several previous measurements done with V2 centers including anti-Stokes excitation39, ODMR with off-resonant readout28, as well as

autocorrelation of resonator-integrated defects16. Our work also explains the main differences between V1 and V2 centers in 4H-SiC. The unraveled understanding of the complete spin-optical

dynamics of the V2 center provides the critical engineering guidelines towards its integration into nanophotonic enhancement structures, such as waveguides and resonators. To showcase this,

we additionally propose realistic protocols for generating time-bin entangled multi-photon GHZ and cluster states, taking advantage of the high quantum efficiency of the O2 transition. We

provide in-depth analysis of state fidelities, optimization of pulse timings, and minimum Purcell enhancement requirements for generating GHZ or cluster states of various sizes. We show that

two-photon GHZ and cluster states can be readily realized with existing SiC nanophotonic resonators, whereas higher photon-number states would require further improvements. In this sense,

we believe that phonon or strain engineering of V2 centers will become necessary to suppress excitation errors by increasing the excited state zero-field splitting, and to improve the

overall branching ratio. Overall, our studies provide a holistic summary on the intrinsic spin-optical dynamics of the V2 center in 4H-SiC. This now permits defining ideal experimental

protocols and routines for maximizing the performance in various quantum technology applications, as well as optimizing the optical performance of V2 centers via integration into

nanophotonic resonators. Additionally, our methods can be straightforwardly adapted to improve the understanding of internal spin dynamics of other color centers. METHODS EXPERIMENTAL SETUP

All the experiments are performed with a home-built scanning confocal microscope at 5.5 K in a closed-cycle cryostat (Montana Instruments). The resonant excitation of the single V2 color

center uses a tunable single-frequency diode laser (Toptica DLC DL pro) at 916.5 nm. The acousto-optic modulator (Gooch&Housego) and electro-optic amplitude modulator (Jenoptik) enable

continuous-wave and pulsed excitation resonantly. A custom-made diode laser is employed for off-resonant excitation at 730 nm. A polarization-maintaining fiber combines all excitation lasers

which are focused onto the sample by a microscope objective (Zeiss EC Epiplan-Neofluar ×100, NA = 0.9). The scanning of the sample is enabled by a fast-steering mirror (Mad City Labs). The

fluorescence emission is collected at phonon-side bands (940–1033 nm) by a superconducting nanowire single photon detector (Photon Spot). The fabrication of the 4H-SiC sample, defect

generation, and development of a solid immersion lens have been described in our previous work10. DENSITY MATRIX MASTER EQUATION PARAMETER OPTIMIZATION The resonant PL decay of the V2 defect

can be accurately modeled by using the fine structure and ISC model in Fig. 1b. The spin-selective fluorescence signal corresponds to the time-dependent excited state populations, that are

calculated using the following master equation, \(\rho /{dt}=-\frac{i}{\hslash }[{H}_{0},\rho ]+{\gamma }_{{\rm{r}}}{\sum }_{{\rm{i}}=1}^{2}L({A}_{{\rm{r}}}^{i})+{\sum

}_{{\rm{i}}=1}^{4}{\gamma }_{i}L({A}_{{\rm{m}}{{\rm{s}}}_{1}}^{i})+{\sum }_{{\rm{i}}=1}^{4}{\gamma }_{i}^{{\prime} }L({A}_{{\rm{m}}{{\rm{s}}}_{2}}^{i})\). The radiative and non-radiative

decay processes are represented by the Lindblad super-operators, _L_(_O_). The _H_0 is the Hamiltonian constructed from optically driven spin ±1⁄2 and ±3⁄2 ground and excited states,

\({H}_{0}=({D}_{{\rm{g}}}-{D}_{{\rm{e}}}-{\delta }_{{\rm{L}}})(|{{\rm{gs}}}_{1/2}\rangle \langle {{\rm{gs}}}_{1/2}|-|{{\rm{es}}}_{1/2}\rangle \langle

{{\rm{es}}}_{1/2}|)-({D}_{{\rm{g}}}-{D}_{{\rm{e}}}-{\delta }_{{\rm{L}}})(|{{\rm{gs}}}_{3/2}\rangle \langle {{\rm{gs}}}_{3/2}|-|{{\rm{es}}}_{3/2}\rangle \langle {{\rm{es}}}_{3/2}|)+[{\Omega

}_{{\rm{L}}}(|{{\rm{gs}}}_{1/2}\rangle \langle {{\rm{es}}}_{1/2}|+|{{\rm{gs}}}_{3/2}\rangle \langle {{\rm{es}}}_{3/2}|)+h.c.]\) in the rotating frame of the laser with power dependent Rabi

frequency ΩL and detuning \({\delta }_{{\rm{L}}}={{\omega }_{{\rm{L}}}-\omega }_{{\rm{ZPL}}}\). The radiative decays, \({A}_{{\rm{r}}}^{i}=|{{\rm{gs}}}_{i}\rangle \langle {{\rm{es}}}_{i}|\),

are governed by the same radiative decay rates _γ_r for both O1 and O2 transitions. The non-radiative ISC decays in and out of each metastable state (\({{\rm{ms}}}_{1}=v{e}^{2}\) and

\({{\rm{ms}}}_{2}={v}^{2}e\)) are given by \({A}_{{{\rm{ms}}}_{1}}^{i}=|{{\rm{ms}}}_{1}\rangle \langle {{\varphi }}_{i}|\) and \({A}_{{{\rm{ms}}}_{2}}^{i}=\left|{{\rm{ms}}}_{2}\right\rangle

\langle {{\varphi }}_{i}|\) in which \({{\varphi }}_{\{i=\mathrm{1,2,3,4}\}}=\{{{\rm{es}}}_{1/2},{{\rm{es}}}_{3/2},{{\rm{gs}}}_{1/2},{{\rm{gs}}}_{3/2}\}\) after the effective rate

simplification with \({\gamma }_{{\rm{n}}1}\gg {\gamma }_{\mathrm{3,4}}\) and \({\gamma }_{{\rm{n}}2}\ll {\gamma }_{\mathrm{3,4}}^{{\prime} }\). We use a custom-built parameter optimization

algorithm based on both Nelder–Mead and differential evolution numerical nonlinear optimization methods for simultaneously fitting the excited state population solutions of separate master

equations at four different laser powers with the time dependent photoluminescence decay measurement data. At each trial, a secondary simplified master equation reflecting the 100 ns

integration window for pulse sequence in Fig. 1c is used to also evaluate the fit quality of each rate solution with the delayed pulse measurement data. DATA AVAILABILITY The data presented

in this manuscript are available at the data repository of the University of Stuttgart under https://doi.org/10.18419/darus-4226. CODE AVAILABILITY The codes used in this manuscript are

available from the corresponding authors on reasonable request. REFERENCES * Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced

solid-state spins. _Nat. Photonics_ 12, 516–527 (2018). Article  ADS  Google Scholar  * Bradley, C. E. et al. A ten-qubit solid-state spin register with quantum memory up to one minute.

_Phys. Rev. X_ 9, 031045 (2019). Google Scholar  * Pompili, M. et al. Realization of a multinode quantum network of remote solid-state qubits. _Science_ 372, 259–264 (2021). Article  ADS 

Google Scholar  * Stas, P.-J. et al. Robust multi-qubit quantum network node with integrated error detection. _Science_ 378, 557–560 (2022). Article  ADS  Google Scholar  * Castelletto, S.

& Boretti, A. Silicon carbide color centers for quantum applications. _J. Phys. Photonics_ 2, 022001 (2020). Article  ADS  Google Scholar  * Röder, R. et al. Transition metal and rare

earth element doped zinc oxide nanowires for optoelectronics. _Phys. Status Solidi (b)_ 256, 1800604 (2019). Article  ADS  Google Scholar  * Vaidya, S., Gao, X., Dikshit, S., Aharonovich, I.

& Li, T. Quantum sensing and imaging with spin defects in hexagonal boron nitride. _Adv. Phys. X_ 8, 2206049 (2023). Google Scholar  * Widmann, M. et al. Coherent control of single

spins in silicon carbide at room temperature. _Nat. Mater._ 14, 164–168 (2015). Article  ADS  Google Scholar  * Christle, D. J. et al. Isolated electron spins in silicon carbide with

millisecond coherence times. _Nat. Mater._ 14, 160–163 (2015). Article  ADS  Google Scholar  * Nagy, R. et al. High-fidelity spin and optical control of single silicon-vacancy centres in

silicon carbide. _Nat. Commun._ 10, 1954 (2019). Article  ADS  Google Scholar  * Morioka, N. et al. Spin-controlled generation of indistinguishable and distinguishable photons from silicon

vacancy centres in silicon carbide. _Nat. Commun._ 11, 2516 (2020). Article  ADS  Google Scholar  * Bourassa, A. et al. Entanglement and control of single nuclear spins in isotopically

engineered silicon carbide. _Nat. Mater._ 19, 1319–1325 (2020). Article  ADS  Google Scholar  * Anderson, C. P. et al. Five-second coherence of a single spin with single-shot readout in

silicon carbide. _Sci. Adv._ 8, eabm5912 (2022). Article  ADS  Google Scholar  * Babin, C. et al. Fabrication and nanophotonic waveguide integration of silicon carbide colour centres with

preserved spin-optical coherence. _Nat. Mater._ 21, 67–73 (2022). Article  ADS  MathSciNet  Google Scholar  * Crook, A. L. et al. Purcell enhancement of a single silicon carbide color center

with coherent spin control. _Nano Lett._ 20, 3427–3434 (2020). Article  ADS  Google Scholar  * Lukin, D. M. et al. Two-emitter multimode cavity quantum electrodynamics in thin-film silicon

carbide photonics. _Phys. Rev. X_ 13, 011005 (2023). Google Scholar  * Day, A. M., Dietz, J. R., Sutula, M., Yeh, M. & Hu, E. L. Laser writing of spin defects in nanophotonic cavities.

_Nat. Mater_. 22, 696–702 (2023). * Lukin, D. M. et al. 4H-silicon-carbide-on-insulator for integrated quantum and nonlinear photonics. _Nat. Photon._ 14, 330–334 (2020). Article  ADS 

Google Scholar  * Fang, R.-Z. et al. Experimental generation of spin-photon entanglement in silicon carbide. _Phys. Rev. Lett._ 132, 160801 (2024). Article  ADS  Google Scholar  *

Greenberger, D. M., Horne, M. A. & Zeilinger, A. _Going Beyond Bell’s Theorem_, 69–72 (Springer Netherlands, Dordrecht, 1989). * Schwartz, I. et al. Deterministic generation of a cluster

state of entangled photons. _Science_ 354, 434–437 (2016). Article  ADS  Google Scholar  * Morioka, N. et al. Spin-optical dynamics and quantum efficiency of a single V1 center in silicon

carbide. _Phys. Rev. Appl._ 17, 054005 (2022). Article  ADS  Google Scholar  * Soykal, O. O., Dev, P. & Economou, S. E. Silicon vacancy center in 4H-SiC: Electronic structure and

spin-photon interfaces. _Phys. Rev. B_ 93, 081207 (2016). Article  ADS  Google Scholar  * Dong, W., Doherty, M. W. & Economou, S. E. Spin polarization through intersystem crossing in the

silicon vacancy of silicon carbide. _Phys. Rev. B_ 99, 184102 (2019). Article  ADS  Google Scholar  * Udvarhelyi, P. et al. Spectrally stable defect qubits with no inversion symmetry for

robust spin-to-photon interface. _Phys. Rev. Appl._ 11, 044022 (2019). Article  ADS  Google Scholar  * Simin, D. et al. All-optical dc nanotesla magnetometry using silicon vacancy fine

structure in isotopically purified silicon carbide. _Phys. Rev. X_ 6, 031014 (2016). Google Scholar  * Fuchs, F. et al. Engineering near-infrared single-photon emitters with optically active

spins in ultrapure silicon carbide. _Nat. Commun._ 6, 7578 (2015). Article  ADS  Google Scholar  * Singh, H. et al. Characterization of single shallow silicon-vacancy centers in 4H-SiC.

_Phys. Rev. B_ 107, 134117 (2023). Article  ADS  Google Scholar  * Robledo, L., Bernien, H., Van der Sar, T. & Hanson, R. Spin dynamics in the optical cycle of single nitrogen-vacancy

centres in diamond. _N. J. Phys._ 13, 025013 (2011). Article  Google Scholar  * Niethammer, M. et al. Coherent electrical readout of defect spins in silicon carbide by photoionization at

ambient conditions. _Nat. Commun._ 10, 5569 (2019). Article  ADS  Google Scholar  * Banks, H. B. et al. Resonant optical spin initialization and readout of single silicon vacancies in

4H-SiC. _Phys. Rev. Appl._ 11, 024013 (2019). Article  ADS  Google Scholar  * Udvarhelyi, P. et al. Vibronic states and their effect on the temperature and strain dependence of

silicon-vacancy qubits in 4H-SiC. _Phys. Rev. Appl._ 13, 054017 (2020). Article  ADS  Google Scholar  * Tiurev, K. et al. Fidelity of time-bin-entangled multiphoton states from a quantum

emitter. _Phys. Rev. A_ 104, 052604 (2021). Article  ADS  Google Scholar  * Childress, L. et al. Coherent dynamics of coupled electron and nuclear spin qubits in diamond. _Science_ 314,

281–285 (2006). Article  ADS  Google Scholar  * Bracher, D. O., Zhang, X. & Hu, E. L. Selective Purcell enhancement of two closely linked zero-phonon transitions of a silicon carbide

color center. _Proc. Natl Acad. Sci. USA_ 114, 4060–4065 (2017). Article  ADS  Google Scholar  * Falk, A. L. et al. Electrically and mechanically tunable electron spins in silicon carbide

color centers. _Phys. Rev. Lett._ 112, 187601 (2014). Article  ADS  Google Scholar  * Hesselmeier, E. et al. Qudit-based spectroscopy for measurement and control of nuclear-spin qubits in

silicon carbide. _Phys. Rev. Lett._ 132, 090601 (2024). Article  ADS  Google Scholar  * Borregaard, J. et al. One-way quantum repeater based on near-deterministic photon-emitter interfaces.

_Phys. Rev. X_ 10, 021071 (2020). Google Scholar  * Wang, J.-F. et al. Robust coherent control of solid-state spin qubits using anti-Stokes excitation. _Nat. Commun._ 12, 3223 (2021).

Article  ADS  Google Scholar  Download references ACKNOWLEDGEMENTS We acknowledge fruitful discussions with Petr Siyushev, Jianpei Geng, Naoya Morioka, Daniil Lukin and Melissa Guidry. D.L.,

F.K., V.B., E.H., T.S. and J.W. acknowledge support from the European Commission for the Quantum Technology Flagship project QIA (Grant agreements 101080128 and 101102140), the German

ministry of education and research for the projects InQuRe, QR.X, Spinning (BMBF, Grants No. 16KIS1639K, No. 16KISQ013, and No. 13N16219) and INST 41/1109-1 FUGG, as well as the Ministerium

für Wirtschaft, Arbeit und Tourismus Baden-Württemberg for the project SPOC (Grant Agreement No. QT-6). F.K. acknowledges funding by the Luxembourg National Research Fund (FNR) (project:

17792569). F.K., J.U.H, and J.W. acknowledge support from the European Commission through the QuantERA project InQuRe (Grant Agreements No. 731473 and No. 101017733). J.U.H. acknowledges

support from the Swedish Research Council under VR Grant No. 2020-05444. N.T.S. and J.U.H. acknowledge support from EU H2020 project QuanTELCO (Grant No. 862721), and the Knut and Alice

Wallenberg Foundation (Grant No. KAW 2018.0071). Ö.O.S. acknowledges support from Booz Allen Hamilton Inc. T.O. acknowledges funding from the Japan Society for the Promotion of Science via

the grant JSPS KAKENHI 21H04553, as well as the Japan Science and Technology Agency for funding within the MEXT Q-LEAP program via the grant JPMXS0118067395. FUNDING Open Access funding

enabled and organized by Projekt DEAL. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * 3rd Institute of Physics, IQST, and Research Center SCoPE, University of Stuttgart, Stuttgart, 70569,

Germany Di Liu, Vladislav Bushmakin, Erik Hesselmeier, Timo Steidl & Jörg Wrachtrup * Materials Research and Technology (MRT) Department, Luxembourg Institute of Science and Technology

(LIST), Belvaux, 4422, Luxembourg Florian Kaiser * National Institutes for Quantum Science and Technology (QST), 1233 Watanuki, Takasaki, Gunma, 370-1292, Japan Takeshi Ohshima * Department

of Materials Science, Tohoku University, 6-6-02 Aramaki-Aza, Aoba-ku, Sendai, 980-8579, Japan Takeshi Ohshima * Department of Physics, Chemistry and Biology, Linköping University, Linköping,

581 83, Sweden Nguyen Tien Son & Jawad Ul-Hassan * Booz Allen Hamilton Inc., McLean, Virginia, 22102, USA Öney O. Soykal * Photonic Inc., Coquitlam, British Columbia, V3K 6T1, Canada

Öney O. Soykal Authors * Di Liu View author publications You can also search for this author inPubMed Google Scholar * Florian Kaiser View author publications You can also search for this

author inPubMed Google Scholar * Vladislav Bushmakin View author publications You can also search for this author inPubMed Google Scholar * Erik Hesselmeier View author publications You can

also search for this author inPubMed Google Scholar * Timo Steidl View author publications You can also search for this author inPubMed Google Scholar * Takeshi Ohshima View author

publications You can also search for this author inPubMed Google Scholar * Nguyen Tien Son View author publications You can also search for this author inPubMed Google Scholar * Jawad

Ul-Hassan View author publications You can also search for this author inPubMed Google Scholar * Öney O. Soykal View author publications You can also search for this author inPubMed Google

Scholar * Jörg Wrachtrup View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.L., F.K., Ö.O.S and J.W. conceived and designed the experiments.

D.L. and F.K. performed the experiments. D.L. and Ö.O.S. analyzed the data. Ö.O.S. developed the theoretical modeling and simulations. D.L. and Ö.O.S. carried out the numerical simulations.

J.U.-H. provided the SiC sample. T.O. and N.T.S. irradiated the SiC with electrons for defect generation. F.K., V.B., E.H., T.S. and J.W. assisted the data analysis. D.L., F.K. and Ö.O.S.

wrote the manuscript with helpful inputs from all the authors. CORRESPONDING AUTHORS Correspondence to Öney O. Soykal or Jörg Wrachtrup. ETHICS DECLARATIONS COMPETING INTERESTS The authors

declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

SUPPLEMENTARY INFORMATION 41534_2024_861_MOESM1_ESM.PDF Supplementary Information for: The silicon vacancy centers in SiC: determination of intrinsic spin dynamics for integrated quantum

photonics RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and

reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Liu, D., Kaiser, F., Bushmakin, V. _et al._ The silicon vacancy centers in SiC: determination of intrinsic spin dynamics for integrated quantum photonics. _npj Quantum Inf_ 10, 72

(2024). https://doi.org/10.1038/s41534-024-00861-6 Download citation * Received: 03 August 2023 * Accepted: 21 June 2024 * Published: 23 July 2024 * DOI:

https://doi.org/10.1038/s41534-024-00861-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative