Reader TTS

ABSTRACT Quantum magnets admit more than one classical limit and _N_-level systems with strong single-ion anisotropy are expected to be described by a classical approximation based on

SU(_N_) coherent states. Here we test this hypothesis by modeling finite temperature inelastic neutron scattering (INS) data of the effective spin-one antiferromagnet Ba2FeSi2O7. The

measured dynamic structure factor is calculated with a generalized Landau-Lifshitz dynamics for SU(3) spins. Unlike the traditional classical limit based on SU(2) coherent states, the

results obtained with classical SU(3) spins are in good agreement with the measured temperature dependent spectrum. The SU(3) approach developed here provides a general framework to

understand the broad class of materials comprising weakly coupled antiferromagnetic dimers, trimers, or tetramers, and magnets with strong single-ion anisotropy. SIMILAR CONTENT BEING VIEWED

BY OTHERS ANOMALOUS CONTINUUM SCATTERING AND HIGHER-ORDER VAN HOVE SINGULARITY IN THE STRONGLY ANISOTROPIC _S_ = 1/2 TRIANGULAR LATTICE ANTIFERROMAGNET Article Open access 23 August 2024

FIELD-INDUCED BOUND-STATE CONDENSATION AND SPIN-NEMATIC PHASE IN SRCU2(BO3)2 REVEALED BY NEUTRON SCATTERING UP TO 25.9 T Article Open access 10 January 2024 DIMENSIONAL REDUCTION AND

INCOMMENSURATE DYNAMIC CORRELATIONS IN THE \(S=\FRAC{1}{2}\) TRIANGULAR-LATTICE ANTIFERROMAGNET CA3REO5CL2 Article Open access 23 October 2022 INTRODUCTION The computation of dynamical

correlation functions at finite temperature is one of the important open problems of modern quantum many-body physics. These functions are not only crucial to test models against different

spectroscopic techniques, but are also critical to the development of fast machine learning tools to accelerate and enhance understanding of problems at the forefront of condensed matter

physics. For instance, the inelastic neutron scattering (INS) cross-section of quantum magnets is proportional to the dynamical spin structure factor, _S_(Q, _E_). A full calculation of this

dynamical correlation function is complex because of the exponential numerical cost of computing the exact Hamiltonian eigenstates as a function of the number of spins _N_s. To surmount

this challenge, classical approximations such as Landau-Lifshitz dynamics (LLD) have been extensively adopted and applied1,2,3,4,5,6 because their numerical cost becomes linear in _N__s_.

Furthermore, while semi-classical approaches7,8,9 are only applicable at the lowest temperatures (because fluctuations around the classical ground state are assumed to be small), the

classical approach, based on the LLD, can be implemented at any temperature by sampling initial states via the Metropolis algorithm (classical Monte Carlo simulation) and solving the

classical equations of motion. Therefore, the LLD and its generalizations can be used to compute dynamical spin structure factors over the full temperature range. Furthermore, the

possibility to determine a Hamiltonian in the more tractable classical limit is important since a classical description is expected to become a good approximation at high enough

temperatures. An approach of this type can even be applied to materials that exhibit strong quantum fluctuations at low temperatures, such as spin liquid candidates3. LLD was originally

introduced to describe the precession of the magnetization in a solid10. This dynamics can be derived as a classical limit of quantum spin systems, whose quantum mechanical state becomes a

direct product of SU(2) coherent states. The time evolution of this product state is dictated by the LLD equations. It is known, however, that _N_-level quantum mechanical systems (_N_ = 

2_S_ + 1 for spin systems) admit more than one classical limit11,12,13,14,15,16,17,18. As was pointed out in a recent work19, there are large classes of low-entangled quantum magnets, such

as materials with strong single-ion anisotropy, for which it is necessary to use a generalized spin dynamics (GSD) which accounts for non-dipolar components of spin states (non-zero

expectation values of other multipoles). This GSD is also necessary to describe magnets with significant biquadratic interactions7,20 and those comprising weakly-coupled entangled units,

such as dimers21,22, trimers23, and tetramers24,25,26,27. The hypothesis that the present work seeks to test is that these systems are better described by direct products of SU(_N_) coherent

states at any temperature. This implies that the traditional LLD must be extended to encompass these more general cases19. The main goal of this work is to test the aforementioned

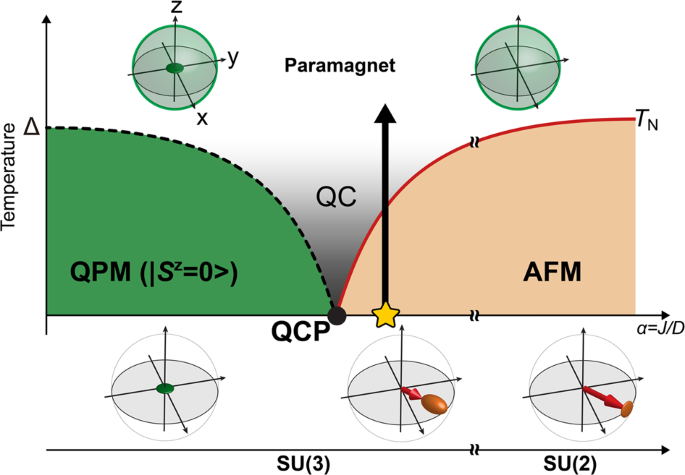
hypothesis by modeling the INS cross-section of the effective _S_ = 1 quasi-2D easy-plane antiferromagnet (AFM), Ba2FeSi2O728,29. In Ba2FeSi2O7, a significant single-ion anisotropy (_D_ ~ 

1.42 meV) induced by the large tetragonal distortion of FeO4 tetrahedron in conjunction with spin-orbit coupling of Fe2+(3_d_6) results in an effective low-energy three-level manifold

generated by the spin states, \(\left\vert {S}^{z}=0,\pm 1\right\rangle\). The competition with a relatively weak Heisenberg exchange interaction, places the ground state of this material

(_α_=_J_/_D_ ~ 0.187) near the quantum critical point at _α__c_ ~ 0.158 that separates easy-planar AFM order from a quantum paramagnetic (QPM) phase (see Fig. 1). Since the AFM to QPM

transition is driven by an enhancement of the local quadrupolar moment at the expense of the magnitude of the local dipolar moment, a proper classical description must allow for the

coexistence of local dipolar and quadrupolar fluctuations, leading to transverse and longitudinal collective modes28. SU(3) coherent states fulfill this condition because an SU(3) spin has 8

 = 3 + 5 components that include the three components of the dipole moment and the five components of the quadupolar moment (trace-less symmetric tensor)7,19,30,31,32. In this article, we

use INS to explore the temperature dependence of _S_(Q, _E_) for Ba2FeSi2O7. The spin excitation spectra exhibit significant transfer of spectral weight across the Néel temperature (_T_N = 

5.2 K) with a continuous evolution from well-defined SU(3) spin-wave modes for _T_ < _T_N to a diffusive resonant excitation for _T_ > _T_N, indicating temperature dependent spin

dynamics. To account for this behavior, we generalize LLD to SU(3) coherent states. This GSD combined with Monte Carlo simulation for temperature dependent classical SU(3) coherent spin

states19 describes the observed temperature dependence of _S_(Q, _E_) both above and below _T_N. This result verifies the main hypothesis of this work, namely that many anisotropic magnets

such as Ba2FeSi2O7 can be described by direct products of SU(_N_) coherent states at any temperature. RESULTS TEMPERATURE DEPENDENT INELASTIC NEUTRON SCATTERING SPECTRA Figure 2a shows the

temperature dependence of the unpolarized neutron cross-section _I_(Q,_E_) of Ba2FeSi2O7, which is proportional to _S_(Q, _E_). Below _T_N, the spectrum exhibits sharp spin-waves

corresponding to acoustic (_T_1) and optical (_T_2) transverse modes. The longitudinal (_L_) mode is observed as a broad continuum above the _T_1-mode throughout the entire Brillouin zone

(BZ) due to decay into a pair of transverse modes as described in ref. 28. While the sharp spin-waves disappear above _T_N, a broad dispersion with a finite gap emerges at the magnetic zone

center (ZC), Q_m_ = (1, 0, 0.5). With increasing temperature, the gap size increases and the bandwidth becomes narrower. To understand the diffusive spectra above _T_N, we performed a

polarized neutron scattering experiment. Figure 2c shows the neutron spin polarization dependence of _I_(_E_) at Q = (1, 0, 0). The spin-flip and nonspin-flip scattering cross-sections are

coupled to the sample magnetization and the wave-vector, allowing us to extract the directional dependence of _S_(Q,_E_). The neutron spin was polarized along [0, 1, 0], which provides

separate in-plane (_S_⊥ = _S__x__x_(Q, _E_) + _S__y__y_(Q, _E_)) and out-of plane (_S_∥ = _S__z__z_(Q, _E_)) components of _S_(Q, _E_), for nonspin-flip and spin-flip channels, respectively.

The nonspin-flip channel is by far the most intense, indicating the diffusive spectra at 10 K mainly comes from the in-plane components of _S_(Q, _E_). CALCULATION OF GENERALIZED SPIN

DYNAMICS FOR SU(3) SPIN To account for the measured spectra at finite temperatures, we performed GSD calculations. The low-energy effective Hamiltonian for Ba2FeSi2O7 is

\({{{\mathcal{H}}}}={\sum }_{{{{\boldsymbol{r}}}},{{{\boldsymbol{\delta }}}}}{S}_{{{{\boldsymbol{r}}}}}^{\mu }{{{{\mathcal{J}}}}}_{{{{\boldsymbol{\delta }}}}}^{\mu \nu

}{S}_{{{{\boldsymbol{r}}}}+{{{\boldsymbol{\delta }}}}}^{\nu }+D{\sum }_{{{{\boldsymbol{r}}}}}{({S}_{{{{\boldsymbol{r}}}}}^{z})}^{2}\)28, with the convention of summation over repeated

indices _μ_, _ν_ = {_x_, _y_, _z_} and _Δ_ runs over the neighboring bonds with finite exchange interaction. This Hamiltonian can be recast in terms of SU(3) generators

\({\hat{O}}_{{{{\boldsymbol{r}}}}}^{\eta }\)19 $$\hat{{{{\mathcal{H}}}}}=\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{r}}}},{{{\boldsymbol{\delta

}}}}}{\hat{O}}_{{{{\boldsymbol{r}}}}}^{\eta }{{{{\mathcal{J}}}}}_{{{{\boldsymbol{\delta }}}}}^{\eta \gamma }{\hat{O}}_{{{{\boldsymbol{r}}}}+{{{\boldsymbol{\delta }}}}}^{\gamma

}+\frac{D}{\sqrt{3}}\mathop{\sum}\limits_{{{{\boldsymbol{r}}}}}\left({\hat{O}}_{{{{\boldsymbol{r}}}}}^{8}+\frac{2}{\sqrt{3}}\right),$$ (1) where the exchange tensor

\({{{{\mathcal{J}}}}}_{{{{\boldsymbol{\delta }}}}}^{\eta \gamma }={\delta }_{\eta \gamma }{J}_{{{{\boldsymbol{\delta }}}}}({\delta }_{\eta 1}+{\delta }_{\eta 2}+{\delta }_{\eta 3}{{{\Delta

}}}_{{{{\boldsymbol{\delta }}}}})\) with \({J}_{{{{\boldsymbol{\delta }}}}}=J(J^{\prime} )\), \({{{\Delta }}}_{{{{\boldsymbol{\delta }}}}}={{\Delta }}({{\Delta }}^{\prime} )\) for

nearest-neighbor intralayer (interlayer) bonds and 1 ≤ _η_, _γ_ ≤ 8. The generators \({\hat{O}}_{{{{\boldsymbol{r}}}}}^{1-3}\) correspond to _dipolar_ operators

\(({S}_{{{{\boldsymbol{r}}}}}^{x},{S}_{{{{\boldsymbol{r}}}}}^{y},{S}_{{{{\boldsymbol{r}}}}}^{z})\) and \({\hat{O}}^{4-8}\) are the _quadrupolar_ operators (bilinear traceless forms of the

dipolar operators). See ref. 19 for the matrix representations. We note that the single-ion anisotropy becomes an external (quadrupolar) field that is linearly coupled to the SU(3) spins.

After taking the classical limit of Eq. (1) using SU(3) coherent states19, \({\hat{O}}_{{{{\boldsymbol{r}}}}}^{\eta }\to {o}_{{{{\boldsymbol{r}}}}}^{\eta }\equiv \left\langle

{Z}_{{{{\boldsymbol{r}}}}}\right\vert {\hat{O}}_{{{{\boldsymbol{r}}}}}^{\eta }\left\vert {Z}_{{{{\boldsymbol{r}}}}}\right\rangle\), we obtain the classical equation of motion (EOM) of the

SU(3) spins $$\frac{d{o}_{{{{\boldsymbol{r}}}}}^{\eta }}{dt}=\mathop{\sum}\limits_{{{{\boldsymbol{\delta }}}}}{{{{\mathcal{J}}}}}_{{{{\boldsymbol{\delta }}}}}^{\gamma \alpha }{f}_{\eta

\gamma \lambda }{o}_{{{{\boldsymbol{r}}}}}^{\lambda }{o}_{{{{\boldsymbol{r}}}}+{{{\boldsymbol{\delta }}}}}^{\alpha }+\frac{D}{\sqrt{3}}{f}_{\eta 8\lambda }{o}_{{{{\boldsymbol{r}}}}}^{\lambda

},$$ (2) where _f__η__γ__λ_ are the SU(3) structure constants: \([{\hat{O}}_{{{{\boldsymbol{r}}}}}^{\eta },{\hat{O}}_{{{{\boldsymbol{r}}}}}^{\gamma }]=i{f}_{\eta \gamma \lambda

}{\hat{O}}_{{{{\boldsymbol{r}}}}}^{\lambda }\). To compute _S_(Q, _E_) at finite temperature, the initial conditions of Eq. (2) are sampled with the standard Metropolis-Hastings Monte Carlo

(MC) algorithm from the CP2 manifold (classical phase space) of SU(3) coherent states (see Supplementary Note 2 for detailed information). The numerical integration methods for the classical

EOM (2) are explained in Supplementary Note 3 and ref. 33. The INS intensity _I_(Q, _E_) is obtained from the Fourier transform of the classical dipolar operators

\({o}_{{{{\boldsymbol{r}}}}}^{\mu }(t)\,\mu =1,2,3\) (see Supplementary Note 2). For the calculation, we used _J_ = 0.266 meV, \(J^{\prime} =0.1J^{\prime}\), and _D_ = 1.42 meV from ref. 28

and finite lattices consisting of 24 × 24 × 12 sites. Additionally, for low values of the spin _S_, the Néel temperature of the classical spin Hamiltonian is significantly lower than the

Néel temperature of the quantum mechanical Hamiltonian because quantum fluctuations further increase the energy gain of the ordered state relative to a disordered state. This is a well-known

fact for the traditional classical limit based on SU(2) coherent states which remains true for the more general case that we are considering here. Hence the classical approximation used

here underestimates the value of Néel temperature, \({T}_{{{{\rm{N}}}}}^{{{{\rm{cl}}}}}=1.38\)K, compared to experimental value _T_N by a factor of ~ 3.75. Therefore in Fig. 2a, b we compare

the measured and calculated spectra at the same values of _T_/_T_N and \({T}^{{{{\rm{cl}}}}}/{T}_{{{{\rm{N}}}}}^{{{{\rm{cl}}}}}\), respectively. COMPARISON OF MEASURED AND CALCULATED

SPECTRA Below _T_N, the calculated spectrum exhibits _T_1-, _T_2- and _L_-modes (see Fig. 2), where the calculated intensities by the GSD are multiplied by the classical to quantum

correspondence factor for a harmonic oscillator \({\beta }^{{{{\rm{cl}}}}}E/(1-{e}^{-{\beta }^{{{{\rm{cl}}}}}E})\) with _β_cl = 1/_k_B_T_cl 34. Since the GSD calculation at low-temperatures

coincides with the generalized _linear_ spin-wave calculation28, the decay and renormalization of the _T_2 and _L_-modes observed at 1.6 K (Fig. 2a) are not captured by this classical

approximation. Capturing these feature requires the nonlinear approach described in ref. 28. Above _T_N, the GSD calculation reproduces the gapped nature of the spectrum representing a

resonant excitation between \(\left\vert {S}^{z}=0\right\rangle\) and \(\left\vert \pm 1\right\rangle\) states with a finite dispersion due to the exchange interaction. In the classical

description, this diffusive mode originates from the combined effect of the “external SU(3) field” _D_ that induces a precession of each SU(3) moment with frequency _D_/ℏ (center of the

peak) and the random molecular field due to the exchange interaction with the fluctuating neighboring moments that determines the width of the peak. When _J_ ≪ _T_, the spectrum thus becomes

a dispersion-less broad peak centered around an energy Δpara ≃ _D_. The computed spectra reproduces the main characteristics of the observed dispersions and bandwidth. Since the

\(\left\vert {S}^{z}=0\right\rangle\) and \(\left\vert \pm 1\right\rangle\) states are connected by the components that are transverse to the _z_-axis, _S_± = _S__x_ ± _i__S__y_, the

corresponding intensity of _S_(Q, _E_) should appear in the channel _S_⊥ = _S__x__x_(Q, _E_)+_S__y__y_(Q, _E_) (see Fig. 2d), which is qualitatively in good agreement with the polarization

dependence of the measured _S_(Q, _E_). The detailed spectral change across _T_N is shown in Fig. 3 which compares the measured and calculated constant momentum scans at the ZC with varying

temperature. For _T_ < _T_N, we consider a wave vector Q = (1, 0, 0.2) that is close but not exactly equal to the ZC Q = (1, 0, 0.5) in order to avoid the large tail of the magnetic Bragg

reflection as well as the technical challenges associated with calculating the spectrum at the ZC. In this case, the _T_1 (Goldstone) mode becomes visible because of its finite energy at Q 

= (1, 0, 0.2) due to the non-zero [0, 0, _L_]-dispersion produced by the small inter-layer coupling _J_inter. As a result, the three _T_1, _T_2, _L_ modes are observed in the spectrum (see

Fig. 3a). While the _T_1 and _T_2 transverse modes remain nearly unchanged with increasing temperature, the energy of the _L_-mode decreases and the mode becomes broader and

indistinguishable from the quasielastic scattering near _T_N. Above _T_N, the quasielastic scattering continuously evolves into a broad peak centered at finite energy (Δpara), whose energy

increases gradually with the temperature (see Fig. 3c). To extract the spectral weight of the resonant excitation above _T_N and the _L_-mode below _T_N, the data were fitted with a double

Lorentzian function associated with a damped harmonic-oscillator (DLDHO), $$S(E)=A(n(E)+1)\left[\frac{{{\Gamma }}}{{(E-{{\Delta }})}^{2}+{{{\Gamma }}}^{2}}-\frac{{{\Gamma }}}{{(E+{{\Delta

}})}^{2}+{{{\Gamma }}}^{2}}\right],$$ (3) that provides a simplified description of the contribution of an over-damped mode35,36. The _n_(_E_) + 1 is the Bose factor, and _A_, Δ, and Γ

indicate the intensity, energy, and line-width of the peak, respectively. The extracted spectral weights and parameters of the _L_-mode and the resonant excitations are indicated by the

shaded regions in Fig. 3a–c, and summarized in Fig. 3d, e, respectively. Figure 3b, c show a comparison of the GSD calculation with the INS data across _T_N. Remarkably, the spectral weight

for the _L_-mode is enhanced and shifts to low-energy with increasing temperature, which is consistent with the data. Above _T_N, the GSD calculation gives a diffusive resonant peak-shaped

spectrum centered at the energy Δpara that approaches _D_ for _T_ ≫ _T_N. We note that the traditional LLD based on SU(2) coherent states cannot explain this gapped diffusive mode as well as

the _L_-mode, leading to incorrect results in the high-temperature limit19. However, we notice that the calculated spectrum underestimates the width of the mode at temperatures _T_ ≳ _T_N.

This discrepancy arises from an inadequate normalization of the SU(3) spins at _T_ ≳ _T_N19, similar to the issue raised in traditional SU(2) LLD37. This discrepancy in the line-width can be

removed in the high-temperature limit by applying an adequate renormalization of the SU(3) spins \({o}_{{{{\boldsymbol{r}}}}}^{\eta }\to \kappa {o}_{{{{\boldsymbol{r}}}}}^{\eta }\), with

_κ_ = 2 in the high-temperature (_T_ ≫ _T_N) limit, as described in Ref. 19. This renormalization guarantees that the SU(3) _S_(Q, _E_) satisfies the exact sum-rule in the high-_T_ limit.

Properly renormalizing the spin has the additional virtue of bringing the theoretical Néel temperature to \({T}_{{{{\rm{N}}}}}^{{{{\rm{cl}}}}}\,\simeq 7.5\)K (_κ_ = 2) closer to the

experimental value _T_N = 5.2 K. Figure 4a shows the comparison between the new calculations including the renormalization factor and the data measured at the same temperature _T_cl = _T_

(experiment). This comparison reveals a better agreement in spectral shape at _T_N ≪ _T_ than those without renormalization factor (see Fig. 3c). As expected, significant deviations in

low-energy spectrum are observed at _T_ = 10 K and 12 K because they are relatively close to the \({T}_{{{{\rm{N}}}}}^{{{{\rm{cl}}}}}\) which deviates from the experimental _T_N. In other

words, since the energy Δpara of the diffusive peak goes to zero at _T_N, its position is shifted to the lower energy relative to the measured peak at _T_ = 10 K. The emergence of a

quasielastic peak (centered at _E_ = 0) in the theoretical calculation indicates proximity to the \({T}_{{{{\rm{N}}}}}^{{{{\rm{cl}}}}}\). Figure 4b, c show the computed INS cross-section,

_I_(Q, _E_), at _T_ = 10 K and 40 K along the same direction in reciprocal space that is presented in Fig. 2a. The _T_ = 10 K and 40 K spectra with renormalized spin provide a good

description of the measured spectra at these temperatures. DISCUSSION In summary, the GSD based on SU(3) spin provides a good approximation of the measured INS cross-section over a broad

temperature range. The most quantitative deviations are observed at very low-temperatures _T_ ≪ _T_N and close to _T_N. The former case is due to the requirement of a one-loop quantum

correction to account for the decay of the _L_-mode28, and the latter is due to the expected discrepancy between the experimental and re-scaled values of _T_N originated from the

renormalization factor _κ_ = 2 to the classical SU(3) spins. This renormalization factor arises from enforcing the sum-rule in the infinite _T_-limit. Similarly, the GSD of unrenormalized

classical SU(3) (_κ_ = 1) leads to the correct sum-rule in the zero temperature limit after quantizing the normal modes. Therefore, the correct scaling factor should be defined as a function

_κ_(_T_) that monotonically interpolates between the two limiting cases _κ_(0) = 1 and _κ_(_∞_) = 2. The verification of the main hypothesis of this work has very important consequences for

the characterization of quantum magnets. For instance, while INS is an ideally suited technique for extracting models from data, the solution of this “inverse scattering problem"

requires the development of fast solvers of the direct problem (inferring the INS cross-section of a given model). A crucial advantage of the GSD demonstrated here is that the cost of the

simulations scales linearly in the system size, while the computation cost of exact dynamics grows exponentially33, making it an ideal solver for attacking the inverse scattering problem

with machine-learning-based approaches4. Moreover, since the GSD can reproduce the INS data in the high-temperature regime, the method can still be applied to quantum magnets that exhibit

long-range entanglement at low enough temperatures, but undergo a quantum to classical crossover above a certain temperature _T_QC3,38. Finally, we note that the SU(_N_) approach described

here is also relevant to the broad class of materials comprising weakly coupled antiferromagnetic magnets including dimers, trimers, or tetramers as well as magnets with strong single-ion

anisotropy, where similar effects may be anticipated. METHODS INELASTIC NEUTRON SCATTERING EXPERIMENT For the INS experiments, the same single crystal of Ba2FeSi2O7 (mass: 2.13 g) as was

used in ref. 28 was aligned on an aluminum plate with an [_H_, 0, _L_] horizontal scattering plane. Unpolarized INS data were collected using the cold neutron triple-axis spectrometer (CTAX)

at the High Flux Isotope Reactor (HFIR) and the hybrid spectrometer (HYSPEC) at the Spallation Neutron Source (SNS) located at Oak Ridge National Laboratory39. A liquid helium cryostat was

used to control temperature for both experiments. At CTAX, the initial neutron energy was selected using a PG (002) monochromator, and the final neutron energy was fixed to _E_f = 3.0 meV by

a PG (002) analyzer. The horizontal collimation was guide − open\(-40^{\prime} -120^{\prime}\), which provides an energy resolution with full width half maximum (FWHM) = 0.1 and 0.18 meV

for _E_ = 0 and 2.5 meV, respectively. For the HYSPEC experiment, _E_i = 9 meV and a Fermi chopper frequency of 300 Hz were used, which gives FWHM = 0.28 meV and 0.19 meV of energy

resolution at _E_ = 0 and 2.5 meV, respectively. Measurements were performed by rotating the sample from − 50° to 170° with 1° steps. Data were integrated over _K_ = [ − 0.16, 0.16] and _L_ 

= [_L_ − 0.1, _L_ + 0.1], and symmetrized over positive and negative _H_. We also performed polarized neutron scattering measurement as part of the HYSPEC experiment using XYZ-polarization

analysis which is the same configuration as the experiment in ref. 40. The X-axis is defined along Q = [1, 0, 0] for the scattering wave vector, the Z-axis is defined along [0, 1, 0]

perpendicular to the scattering plane, and the Y-axis is defined along the direction [0, 0, 1] perpendicular to the X- and Z-axes. In the experiment, the neutron was polarized along the

Z-direction, and the nonspin-flip and spin-flip scattering cross-sections provide \({I}_{{{{\rm{n}}}}}(E)+{I}_{{{{\rm{mag}}}}}^{{{{\rm{Z}}}}}(E)\) and

\({I}_{{{{\rm{mag}}}}}^{{{{\rm{Y}}}}}(E)\), respectively40,41. The _I_n(_E_) indicates non-magnetic structure factor and \({I}_{{{{\rm{mag}}}}}^{\alpha }(E)\), where _α_ ∈ {X, Y, Z}, is the

component dependent magnetic structure factor. The measured spin-flip and nonspin-flip cross-sections provide distinct \({I}_{{{{\rm{mag}}}}}^{{{{\rm{Z}}}}}(E)\) and

\({I}_{{{{\rm{mag}}}}}^{{{{\rm{Y}}}}}(E)\), which correspond to _S__x__x_+_y__y_(_E_) and _S__z__z_(_E_), respectively, on the crystal axis where _x_∥_a_, _y_∥_b_, and _z_∥_c_ in the

tetragonal crystal structure. All of data sets were reduced and analyzed using the MANTID42 and DAVE43 software packages. DATA AVAILABILITY Data are available from the corresponding author

upon reasonable request. REFERENCES * Tsai, S.-H. & Landau, D. P. Spin dynamics: an atomistic simulation tool for magnetic systems. _Comput. Sci. Eng._ 10, 72–79 (2008). Article  Google

Scholar  * Conlon, P. H. & Chalker, J. T. Spin dynamics in pyrochlore Heisenberg antiferromagnets. _Phys. Rev. Lett._ 102, 237206 (2009). Article  ADS  Google Scholar  * Samarakoon, A.

M. et al. Comprehensive study of the dynamics of a classical kitaev spin liquid. _Phys. Rev. B_ 96, 134408 (2017). Article  ADS  Google Scholar  * Samarakoon, A. M. et al.

Machine-learning-assisted insight into spin ice Dy2Ti2O7. _Nat. Commun._ 11, 892 (2020). Article  ADS  Google Scholar  * Lin, S.-Z., Reichhardt, C., Batista, C. D. & Saxena, A. Particle

model for skyrmions in metallic chiral magnets: dynamics, pinning, and creep. _Phys. Rev. B_ 87, 214419 (2013). Article  ADS  Google Scholar  * Zhang, S., Changlani, H. J., Plumb, K. W.,

Tchernyshyov, O. & Moessner, R. Dynamical structure factor of the three-dimensional quantum spin liquid candidate NaCaNi2F7. _Phys. Rev. Lett._ 122, 167203 (2019). Article  ADS  Google

Scholar  * Muniz, R. A., Kato, Y. & Batista, C. D. Generalized spin-wave theory: application to the bilinear-biquadratic model. _Prog. Theor. Exp. Phys._ 2014, 083I01 (2014). Article 

MATH  Google Scholar  * Kohama, Y. et al. Thermal transport and strong mass renormalization in NiCl2-4SC(NH2)2. _Phys. Rev. Lett._ 106, 037203 (2011). Article  ADS  Google Scholar  *

Totsuka, K., Lecheminant, P. & Capponi, S. Semiclassical approach to competing orders in a two-leg spin ladder with ring exchange. _Phys. Rev. B_ 86, 014435 (2012). Article  ADS  Google

Scholar  * Landau, L. & Lifshitz, E. 3 - On the theory of the dispersion of magnetic permeability in ferromagnetic bodies–Reprinted from Physikalische Zeitschrift der Sowjetunion 8, Part

2, 153, 1935. In PITAEVSKI, L. (ed.) _Perspectives in Theoretical Physics_, 51–65 (Pergamon, Amsterdam, 1992). * Glauber, R. J. Photon correlations. _Phys. Rev. Lett._ 10, 84–86 (1963).

Article  ADS  MathSciNet  Google Scholar  * Glauber, R. J. The quantum theory of optical coherence. _Phys. Rev._ 130, 2529–2539 (1963). Article  ADS  MathSciNet  Google Scholar  * Glauber,

R. J. Coherent and incoherent states of the radiation field. _Phys. Rev._ 131, 2766–2788 (1963). Article  ADS  MathSciNet  MATH  Google Scholar  * Sudarshan, E. C. G. Equivalence of

semiclassical and quantum mechanical descriptions of statistical light beams. _Phys. Rev. Lett._ 10, 277–279 (1963). Article  ADS  MathSciNet  MATH  Google Scholar  * Perelomov, A. M.

Coherent states for arbitrary Lie group. _Comm. Math. Phys._ 26, 222–236 (1972). Article  ADS  MathSciNet  MATH  Google Scholar  * Gilmore, R. Geometry of symmetrized states. _Ann. Phys._

74, 391–463 (1972). Article  ADS  MathSciNet  Google Scholar  * Yaffe, L. G. Large _N_ limits as classical mechanics. _Rev. Mod. Phys._ 54, 407–435 (1982). Article  ADS  MathSciNet  Google

Scholar  * Gnutzmann, S. & Kus, M. Coherent states and the classical limit on irreducible representations. _J. Phys. A: Math. Gen._ 31, 9871–9896 (1998). Article  ADS  MathSciNet  MATH 

Google Scholar  * Zhang, H. & Batista, C. D. Classical spin dynamics based on SU(_N_) coherent states. _Phys. Rev. B_ 104, 104409 (2021). Article  ADS  Google Scholar  * Remund, K.,

Pohle, R., Akagi, Y., Romhányi, J. & Shannon, N. Semi-classical simulation of spin-1 magnets. _Phys. Rev. Res._ 4, 033106 (2022). Article  Google Scholar  * Jaime, M. et al.

Magnetic-field-induced condensation of triplons in Han Purple Pigment BaCuSi2O6. _Phys. Rev. Lett._ 93, 087203 (2004). Article  ADS  Google Scholar  * Nawa, K. et al. Triplon band splitting

and topologically protected edge states in the dimerized antiferromagnet. _Nat. Commun._ 10, 1–8 (2019). Article  Google Scholar  * Qiu, Y. et al. Spin-trimer antiferromagnetism in

La4Cu3MoO12. _Phys. Rev. B_ 71, 214439 (2005). Article  ADS  Google Scholar  * Okamoto, Y., Nilsen, G. J., Attfield, J. P. & Hiroi, Z. Breathing pyrochlore lattice realized in _A_-site

ordered spinel oxides LiGaCr4O8 and LiInCr4O8. _Phys. Rev. Lett._ 110, 097203 (2013). Article  ADS  Google Scholar  * Park, S.-Y. et al. Spin–orbit coupled molecular quantum magnetism

realized in inorganic solid. _Nat. Commun._ 7, 1–7 (2016). Article  Google Scholar  * Rau, J. G. et al. Anisotropic exchange within decoupled tetrahedra in the quantum breathing pyrochlore

Ba3Yb2Zn5O11. _Phys. Rev. Lett._ 116, 257204 (2016). Article  ADS  Google Scholar  * Choi, K.-Y. et al. Coexistence of localized and collective magnetism in the coupled-spin-tetrahedra

system Cu4Te5O12Cl4. _Phys. Rev. B_ 90, 184402 (2014). Article  ADS  Google Scholar  * Do, S.-H. et al. Decay and renormalization of a longitudinal mode in a quasi-two-dimensional

antiferromagnet. _Nat. Commun._ 12, 1–12 (2021). Article  ADS  Google Scholar  * Jang, T.-H. et al. Physical properties of the quasi-two-dimensional square lattice antiferromagnet

Ba2FeSi2O7. _Phys. Rev. B_ 104, 214434 (2021). Article  ADS  Google Scholar  * Batista, C. D., Ortiz, G. & Gubernatis, J. E. Unveiling order behind complexity: coexistence of

ferromagnetism and Bose-Einstein condensation. _Phys. Rev. B_ 65, 180402 (2002). Article  ADS  Google Scholar  * Batista, C. D. & Ortiz, G. Algebraic approach to interacting quantum

systems. _Adv. Phys._ 53, 1–82 (2004). Article  ADS  Google Scholar  * H. M, B. Non-Abelian geometric phases carried by the spin fluctuation tensor. _J. Math. Phys._ 59, 062105 (2018).

Article  ADS  MathSciNet  MATH  Google Scholar  * Dahlbom, D. et al. Geometric integration of classical spin dynamics via a mean-field Schrödinger equation. _Phys. Rev. B_ 106, 054423

(2022). Article  ADS  Google Scholar  * Bohm, D. _Quantum theory_ (Courier Corporation, 2012). * Hong, T. et al. Effect of pressure on the quantum spin ladder material IPA - CuCl3. _Phys.

Rev. B_ 78, 224409 (2008). Article  ADS  Google Scholar  * Hong, T. et al. Field induced spontaneous quasiparticle decay and renormalization of quasiparticle dispersion in a quantum

antiferromagnet. _Nat. Commun._ 8, 15148 (2017). Article  ADS  Google Scholar  * Huberman, T., Tennant, D. A., Cowley, R. A., Coldea, R. & Frost, C. D. A study of the quantum classical

crossover in the spin dynamics of the 2D _S_ = 5/2 antiferromagnet Rb2MnF4: neutron scattering, computer simulations and analytic theories. _J. Stat. Mech.: Theory Exp._ 2008, P05017 (2008).

Article  Google Scholar  * Samarakoon, A. M. et al. Classical and quantum spin dynamics of the honeycomb Γ model. _Phys. Rev. B_ 98, 045121 (2018). Article  ADS  Google Scholar  * Winn, B.

et al. Recent progress on HYSPEC, and its polarization analysis capabilities. _EPJ Web Conf._ 83, 03017 (2015). Article  Google Scholar  * Soda, M. et al. Polarization analysis of magnetic

excitation in multiferroic Ba2CoGe2O7. _Phys. Rev. B_ 97, 214437 (2018). Article  ADS  Google Scholar  * Moon, R. M., Riste, T. & Koehler, W. C. Polarization analysis of thermal-neutron

scattering. _Phys. Rev._ 181, 920–931 (1969). Article  ADS  Google Scholar  * Arnold, O. et al. Mantid-data analysis and visualization package for neutron scattering and _μ_SR experiments.

_Nucl. Instrum. Methods Phys. Res. Sect. A: Accelerators, Spectrometers, Detect. Associated Equip._ 764, 156–166 (2014). Article  ADS  Google Scholar  * Azuah, R. et al. DAVE: a

comprehensive software suite for the reduction, visualization, and analysis of low energy neutron spectroscopic data. _J. Res. Natl Inst. Stan. Technol._ 114, 341 (2009). Article  Google

Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division.

This research used resources at the High Flux Isotope Reactor and Spallation Neutron Source, DOE Office of Science User Facilities operated by the Oak Ridge National Laboratory (ORNL). The

work at Max Planck POSTECH/Korea Research Initiative was supported by the National Research Foundation of Korea(NRF) funded by the Ministry of Science and ICT (2020M3H4A2084417 and

2022M3H4A1A04074153) The work at Rutgers University was supported by the DOE under Grant No. DOE: DE-FG02-07ER46382. D.D., K.B., and C.D.B. acknowledge support from U.S. Department of

Energy, Office of Science, Office of Basic Energy Sciences, under Award No. DE-SC0022311. AUTHOR INFORMATION Author notes * These authors contributed equally: Seung-Hwan Do, Hao Zhang.

AUTHORS AND AFFILIATIONS * Materials Science and Technology Division, Oak Ridge National Laboratory, Oak Ridge, TN, USA Seung-Hwan Do, Hao Zhang & Andrew D. Christianson * Department of

Physics and Astronomy, University of Tennessee, Knoxville, TN, USA Hao Zhang, David A. Dahlbom & Cristian D. Batista * Neutron Scattering Division, Oak Ridge National Laboratory, Oak

Ridge, TN, USA Travis J. Williams, V. Ovidiu Garlea & Tao Hong * MPPHC-CPM, Max Planck POSTECH/Korea Research Initiative, Pohang, Republic of Korea Tae-Hwan Jang, Sang-Wook Cheong & 

Jae-Hoon Park * Rutgers Center for Emergent Materials and Department of Physics and Astronomy, Rutgers University, Piscataway, NJ, USA Sang-Wook Cheong * Department of Physics, Pohang

University of Science and Technology, Pohang, Republic of Korea Jae-Hoon Park * Theoretical Division and CNLS, Los Alamos National Laboratory, Los Alamos, NM, USA Kipton Barros Authors *

Seung-Hwan Do View author publications You can also search for this author inPubMed Google Scholar * Hao Zhang View author publications You can also search for this author inPubMed Google

Scholar * David A. Dahlbom View author publications You can also search for this author inPubMed Google Scholar * Travis J. Williams View author publications You can also search for this

author inPubMed Google Scholar * V. Ovidiu Garlea View author publications You can also search for this author inPubMed Google Scholar * Tao Hong View author publications You can also search

for this author inPubMed Google Scholar * Tae-Hwan Jang View author publications You can also search for this author inPubMed Google Scholar * Sang-Wook Cheong View author publications You

can also search for this author inPubMed Google Scholar * Jae-Hoon Park View author publications You can also search for this author inPubMed Google Scholar * Kipton Barros View author

publications You can also search for this author inPubMed Google Scholar * Cristian D. Batista View author publications You can also search for this author inPubMed Google Scholar * Andrew

D. Christianson View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS S.H.D., H.Z., C.D.B., and A.D.C. conceived the project. T.H.J., S.W.C., and

J.-H.P. provided single crystals. S.H.D., T.J.W., T.H., V.O.G., and A.D.C. performed INS experiments. S.H.D., and A.D.C. analyzed the neutron data. H.Z., D.A.D, K.B., and C.D.B. constructed

theoretical model and calculations. S.-H.D., H.Z., C.D.B., and A.D.C. wrote the manuscript with input from all authors. CORRESPONDING AUTHORS Correspondence to Cristian D. Batista or Andrew

D. Christianson. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral with regard to

jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTAL MATERIAL RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are

included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Do, SH., Zhang, H., Dahlbom, D.A. _et al._ Understanding

temperature-dependent SU(3) spin dynamics in the _S_ = 1 antiferromagnet Ba2FeSi2O7. _npj Quantum Mater._ 8, 5 (2023). https://doi.org/10.1038/s41535-022-00526-7 Download citation *

Received: 23 May 2022 * Accepted: 29 November 2022 * Published: 12 January 2023 * DOI: https://doi.org/10.1038/s41535-022-00526-7 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative