Reader TTS

ABSTRACT Heterosis, or hybrid vigour, is said to occur when F1 individuals exhibit increased performance for a number of traits compared to their parental lines. Improved traits can include

increased size, better yield, faster development and a higher tolerance to pathogens or adverse conditions. The molecular basis for the phenomenon remains disputed, despite many decades of

theorising and experimentation. In this study, we add a genetics layer to a constraint-based model of plant (_Arabidopsis_) primary metabolism and show that we can realistically reproduce

and quantify heterosis in a highly complex trait (the rate of biomass production). The results demonstrate that additive effects coupled to the complex patterns of epistasis generated by a

large metabolic network are sufficient to explain most or all the heterosis seen in typical F1 hybrids. Such models provide a simple approach to exploring and understanding heterosis and

should assist in designing breeding strategies to exploit this phenomenon in the future. SIMILAR CONTENT BEING VIEWED BY OTHERS FITNESS CONSEQUENCES OF HYBRIDIZATION IN A PREDOMINANTLY

SELFING SPECIES: INSIGHTS INTO THE ROLE OF DOMINANCE AND EPISTATIC INCOMPATIBILITIES Article 07 August 2021 THE DOMINANCE MODEL FOR HETEROSIS EXPLAINS CULM LENGTH GENETICS IN A HYBRID

SORGHUM VARIETY Article Open access 25 February 2021 INCORPORATING SPATIAL AND GENETIC COMPETITION INTO BREEDING PIPELINES WITH THE R PACKAGE GENCOMP Article 16 January 2025 INTRODUCTION As

early as 1876, Charles Darwin provided the first scientific observations that interspecific hybrids tended to show more vigour than intraspecific hybrids.1 The phenomenon of heterosis has

been recognised for over a century.2 Heterosis can be observed in both plants and animals, and presumably would occur in any diploid organism where such F1 hybrids can be obtained. Animal

and plant breeders have benefited from hybrid vigour to produce increasingly more effective strains. In the USA, the use of hybrid maize has contributed to a dramatic six-fold increase in

yield since the 1930s.3 Its benefits have stimulated extensive study into improving the design and selection of commercially valuable hybrids (reviewed in ref. 4). However, the molecular

explanation for the phenomenon remains a topic of lively discussion. Early studies showed that heterosis was proportional to the genetic distance between two parents.5,6,7 More recent work

has added considerable detail about how the genetic landscape of the parental lines might influence heterosis.8,9 Several competing but not mutually exclusive genetic models have been

proposed in an attempt to provide some mechanistic explanation of the phenomenon. The _dominance_ hypothesis holds that independent sets of deleterious alleles accumulate over time and

particularly during inbreeding of parental lines.5,7 In these conditions, dominant alleles originating from one parent would complement inferior alleles from the second parent, thus

resulting in a phenotypic improvement. The _overdominance_ hypothesis suggests the existence of allelic interactions that induce greater expression of heterozygous loci in hybrids.10,11

Neither of these hypotheses involve interactions between non-allelic loci. Additional hypotheses that do involve such interactions have been proposed. _Pseudo-overdominance_11 is the

appearance of overdominance due to repulsion-phase linkage of dominant alleles.4 The effects of _epistasis_ on heterosis are also becoming increasingly clear as the complexity of the

biological networks underlying multigenic traits becomes better understood.12 Epistasis not only shapes which loci can express heterosis but it can also mimic overdominance.13 All of these

mechanisms could, and probably do, contribute to heterosis. However, debate continues over which are the more important, because of the difficulty in experimentally distinguishing these

intertwined genetic effects. The potential complexity of the mechanisms contributing to heterosis has encouraged attempts to take a ‘systems’ approach to the topic, with large-scale

molecular profiling to analyse gene expression and biochemical phenotypes.14,15,16,17,18,19,20,21,22,23 Such studies have provided much data but perhaps fewer clear explanations than might

be hoped, with different studies reaching different conclusions about which molecular mechanisms predominate. An alternative approach to treating such complexity is to attempt to model it

mathematically or computationally. Modelling allows deliberate simplification of the system to make interpretation of the results easier, either by reducing the number of components, or

their interactions, or both. Genetic models of heterosis have been studied for many years, but generally leave out downstream biological interactions that intervene in the complex interplay

between genotype and phenotype. Only a few attempts have been made to bridge this gap and link genetic models of heterosis to biological networks that can simulate the extent of potential

epistatic interactions between loci, and these have been limited to small-scale networks.13,24 We take this approach a step further by adding a simple genetics layer to a genome-scale model

of plant primary metabolism. This combined model demonstrates plausible levels of heterosis under a set of realistic assumptions based on simple additive effects coupled to epistasis.

RESULTS ADDING GENETICS TO A MODEL OF METABOLISM Standard descriptions of genome-scale metabolic networks do not generally incorporate any notion of genetic variability or heterozygosity,

thus to study heterosis, an additional layer of genetic information is required. We modified a general model of _Arabidopsis_ metabolism25 such that each reaction is assigned to a genetic

locus, and each locus can be assigned a collection of alleles, allowing the simulation of diploid and polyploid individuals. The original metabolic model was designed for flux balance

analysis, in which steady-state metabolic fluxes are calculated for each reaction under external metabolic constraints on the network (e.g. limitations on the rate of photosynthesis). In

general, the metabolic fluxes are optimised to maximise the desired output, for example, biomass production. In our additions to this model, we added internal genetic constraints. Each

allele consists of a constraint that can be applied to a reaction in order to confine its metabolic flux. The rationale behind this is that the genetic information determines the level of

expression and thus the activity of the enzymes in the metabolic network. In the simulations described here, this genetic information acts in _cis_, that is, we have included no

_trans_-acting regulatory factors. This simplification does not prevent heterosis appearing in the simulations because many cross-locus interactions are already provided by the metabolic

network. The constraint attached to each allele was chosen randomly, as follows. First, the generic model was optimised for the maximisation of biomass production (using flux balance

analysis), resulting in a reference flux distribution (RFD). Flux variability analysis (FVA)26 was then performed on the network to calculate an envelope of alternate fluxes for each

reaction that could maintain optimal biomass production. Allele-specific constraints were then generated using the FVA as a guide (such that all alleles had constraints within their

allowable flux range, simulating recurrent natural selection for efficient biomass production). Each individual within the population was assigned two randomly chosen alleles at each locus

(to simulate a heterozygous individual). In simulated crosses, alleles at each locus were transmitted randomly, independently and unaltered; that is, we did not attempt to simulate genetic

linkage, mutation or any epigenetic effects. By default, we assumed that the genetic effects of multiple alleles are additive, that is, we took the average genetic constraints from the

alleles at one locus to set a single constraint for each reaction. Prior to any further calculations, the flux constraints assigned to each individual were normalised such that the sum total

of all constraints corresponds to the sum total of all the fluxes in the RFD. Thus, the total amount of ‘enzyme’ that any individual can produce is fixed in our simulations. This constraint

was introduced to avoid trivial results where rate of biomass production is simply dependent on the total flux capacity (equivalent to the trivial real-life observation that larger

individuals can sustain higher rates of biomass production). Holding total flux capacity constant forces any changes in rate of biomass production in the simulations to be dependent in

changes in metabolic efficiency—producing more interesting outcomes. The biomass production network was then optimised for each individual using the constraints specific to that individual.

Thus, for each reaction in the network, we obtain four flux values (in the case of a diploid individual): the two potential flux constraints encoded by the alleles at the locus, the genetic

flux constraint calculated from these allele values (and subsequent normalisation) that was used during flux balance analysis (henceforth referred to as the enzyme capacity) and the

calculated flux through the reaction following optimisation of biomass production (henceforth referred to as the computed flux). EFFECTS OF SELECTION ON INBREEDING AND HETEROSIS To model the

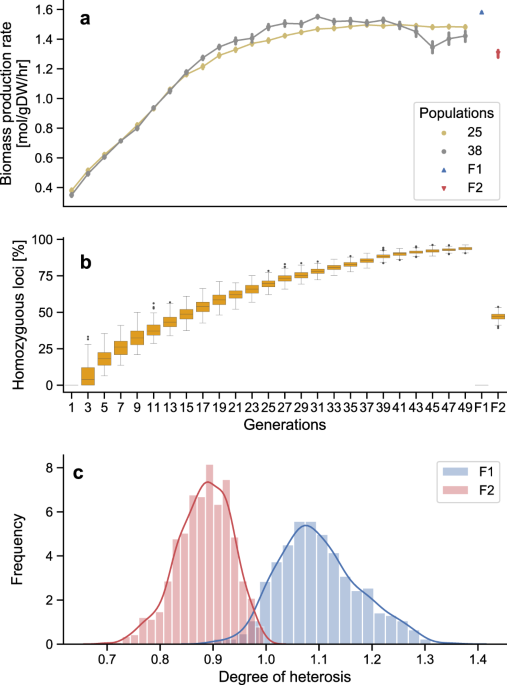
genetic composition of the inbred lines used in conventional breeding programs, we simulated the effect of selection by inbreeding 40 independent heterozygous populations over 50

generations (Supplementary Fig. S1), of which two examples are shown in Fig. 1a. At each generation, the best-performing individuals within each population (judged by rate of biomass

production) were selected and crossed together to generate the following generation of increasingly inbred individuals. Over the first 30 generations, we observed an improvement in the mean

biomass production rate. At the same time, the homozygosity of the population increased (Fig. 1b). In further generations, gains in the rate of biomass production slowed. These general

trends were consistent between the 40 independent populations (and in multiple repeats of this experiment). After 50 generations, when mean homozygosity exceeded 90%, crossing individuals

from two inbred populations produced heterozygous F1 hybrid populations showing heterosis for the rate of biomass production (Fig. 1a). Selfing the F1 populations produced F2 generations

with a lower average rate of biomass production, even lower on average than that of the parental inbreds (Fig. 1c). DIVERSE ROUTES TO HETEROSIS Each individual simulation corresponds to a

linear optimisation problem where an objective function (production of biomass) is maximised. The computed flux through this objective function provides a highly multigenic trait indicative

of overall performance. Detailed analysis of the rest of the metabolic network provides useful information regarding which reactions are contributing to heterosis. In order to identify

reactions contributing to the increased performance in the F1, for each F1 population we calculated the correlation coefficient between the magnitude of heterosis in each F1 individual and

the computed flux for each reaction in the network (Supplementary Table S1). A total of 154 reactions (~34% of the total) were strongly correlated with heterosis (|_r_| > 0.90) in at

least one F1 population. These reactions included both internal reactions and transporters associated with the production of biomass components. Thus, as would be expected, heterosis in

these simulations appears to be due to increased metabolic flux through pathways relevant to biomass production. This can be shown formally by calculating the coupling between each reaction

and the production of biomass.27 Indeed, 90% of the highly correlated reactions were found to be coupled with biomass production (Fig. 2). Nevertheless, not all biomass-coupled reactions

contribute equally to heterosis. SINGLE VS. MULTI-LOCUS CONTRIBUTIONS TO HETEROSIS To examine the contribution of different reactions in the network to heterosis in more detail, we

systematically altered alleles in the F1 individuals to render them homozygous for one or other parental allele at each locus in turn, and recalculated the computed flux for biomass

production. If the recalculated flux was lower than that of the original F1 individual, then this revealed the direct contribution of the altered parental allele to heterosis. Figure 3 shows

a heatmap depicting the direct contribution of all loci calculated in this way. The results indicate that different loci contribute to heterosis in different crosses, as one might expect.

However, the patterns are not entirely random; some loci contribute much more to heterosis than others when viewed across many independent crosses. Thirty-one per cent of the reactions

showed a strong direct contribution to heterosis in at least one F1 population. Surprisingly (at first sight), the loci at which direct contributions are found do not generally correspond to

reactions coupled to biomass production or whose fluxes correlate with heterosis (Fig. 2). This prompted us to look for, and quantify, indirect effects. The direct contributions of all loci

can be summed to give the heterosis arising only from single-locus effects. This in turn can be subtracted from the overall heterosis, leaving the part due to multi-locus effects. The

comparison between these two components of heterosis (Fig. 4 and Supplementary Fig. S2) demonstrates the overriding importance of multi-locus interactions in these simulations. In ~70% of

individuals, multi-locus effects make a larger contribution to heterosis than all the single-locus effects combined, and 40% of individuals show positive heterosis (owing to multi-locus

effects), even though the sum of single-locus effects is negative (individuals coloured in red in the top left quadrant of Fig. 4). HYBRIDS MAKE MORE EFFICIENT USE OF RESOURCES The

efficiency of a reaction in our networks can be defined as the ratio between the computed flux and the enzyme capacity of the reaction (set by the genetic constraints). This represents the

proportion of synthesised enzyme that is actually active. Figure 5 shows that when comparing F1 hybrids to their parents, there is a distinct improvement in reaction efficiencies—a higher

metabolic flux is maintained with equal investment in enzyme synthesis. In particular, there is a sharp increase in the number of reactions operating at near maximal efficiency. This

increase in efficiency underlies heterosis. These efficiency gains are lost in the F2 generation, when the efficiencies return to the level seen in the inbred parents (or even lower).

BIOCHEMICAL MECHANISM: THE RELAXATION OF METABOLIC BOTTLENECKS The presence of many reactions in the network operating at below 100% efficiency implies the presence of metabolic bottlenecks.

These bottlenecks are imposed by the direct genetic constraint on certain metabolic steps. However, they also impact the rest of the network by forcing upstream or downstream reactions to

operate at rates below their maximal capacities. These bottlenecks are partially relaxed in F1 hybrids, as illustrated by the reactions whose efficiency improves. An example provided in Fig.

6 shows how multi-locus effects obtained by crossing parental lines can relax the constraints imposed by specific local bottlenecks, allowing a higher metabolic activity through the whole

pathway. The arrangement of these bottlenecks can be due to random genetic differences in the original populations or due to selection for different biomass production strategies within the

two parental inbred lines. ‘FIXING’ HETEROSIS BY RECURRENT SELECTION It is evident that in the context analysed here, heterosis is largely not dependent on heterozygosity at any locus (i.e.

mixing of parental alleles at one locus), but rather on epistatic effects across two or more loci. If this is the case, then it should be possible to ‘fix’ the improvements obtained in the

F1 generation by selecting for the optimal combinations of parental alleles over subsequent generations. Therefore, we continued to select for biomass production in the F2 and ensuing

generations produced by selfing (Fig. 7). The depression in the rate of biomass production in the F2 was rapidly reversed within a few generations, and from about the F5 generation, the rate

exceeded from that observed in the F1. After approximately six generations, the new ‘inbred’ lines produced were nearing complete homozygosity while preserving rates of biomass production

significantly higher than in the original F1. DISCUSSION Despite substantial efforts to define a universal theory explaining the phenomenon, the understanding of the molecular basis for

heterosis has remained elusive. By reproducing and explaining several, if not all, aspects of heterosis, the modelling approach presented in this study can shed some light on this

long-standing question. The models reproduced the progressive gain in performance and reduction in heterozygosity under intense selection over several generations and the subsequent plateau

as the best alleles become fixed in the population.28,29 The models also demonstrated biologically plausible levels of heterosis, averaging around 10% of increased metabolic flux, which is

in the range of what is commonly observed when crossing typical inbreds. The models also reproduced the collapse of heterosis in the F2 generation. Inspection of the reaction fluxes in the

models provides a rational explanation for the mechanisms responsible for the observed improvement in hybrid F1 plants and allows the investigation and quantification of the contribution of

different aspects of the genetic models. Although the results we obtain appear to mimic heterosis, an obvious question is whether the models we describe accurately reflect a significant

component of the processes underpinning heterosis in living organisms. Our models are necessarily greatly simplified, but we believe they do reproduce the most salient features of the

genetics of heterosis. The results of any computational model are dictated by the choices made in its design; we believe we have made sensible and even conservative decisions in the choices

of the metabolic and genetic models, and in the structure of the populations and the selection regime. As an example of a conservative choice, we used FVA analysis to set the range of the

initial alleles within the population (equivalent to restricting its genetic diversity). Without using FVA to restrict the choice of starting alleles, individuals could contain strongly

sub-optimal alleles (i.e. would be effectively ‘mutants’ in a genetic sense). We felt this would not be a good starting point for simulating heterosis in natural or breeding populations

where recurrent selection will have eliminated almost all strongly sub-optimal alleles even prior to the creation of inbred lines. By reducing the ‘genetic variability’ in the starting

populations, the use of FVA to set the bounds reduces the magnitude of the potential heterosis, but results in a more plausible simulation. An important finding is that simple additive

genetic effects are entirely sufficient to provide significant levels of heterosis without any requirement for dominant or overdominant genetic effects (by this we mean non-additive

interactions between alleles at the same locus). Most experimental observations of gene expression in F1 hybrids have found that additive expression is by far the most common case.15,17,21

This, of course, does not rule out that dominance or overdominance might play important roles in specific instances, and this is supported by genetic studies specifically looking for loci

underlying heterotic effects.18,23,30 Epistatic effects are hard to fully account for in such genetic studies if they involve multiple loci. Similarly, previous attempts to include epistasy

in computational models of heterosis have by and large been limited to effects between two or only a few loci (e.g.31 which underestimates the interconnectivity in most biological contexts).

The importance of epistasy and biological networks in shaping heterosis has been discussed at length4,12 but has been difficult to examine in practice. The originality of connecting a

simple genetic model to a large metabolic network, as we have done, is in the capture of the complex epistatic effects created by the topology of the network. It is clear that in our

simulations, effects involving multiple loci far outweigh the effects of any individual locus, or even of all individual effects summed together. Models such as those we describe should make

it much easier to investigate the contribution of epistasy to heterosis. If inter-locus interactions are more important than intra-locus interactions for heterosis (and in our models this

is certainly the case), then the prediction is that the gains in the F1 generation can be fixed in homozygous inbreds that preserve the best parental allele combinations at different loci.

We showed that in the models this is relatively simple to achieve by recurrent selection over a few generations. This is greatly facilitated in our simplified system by the lack of any

genetic linkage that would interfere with the reassortment of parental alleles. Nevertheless, the results recapitulate a study in _Arabidopsis_, which showed that the improved phenotypic

traits obtained in an F1 hybrid could be stabilised through the generation of the so-called ‘hybrid mimic’ lines.32 Despite the good match of the model outputs to experiment observations of

heterosis, there are many ways in which these models could be improved, or at least extra complexities could be added that may be needed to more finely simulate specific biological contexts.

Our model did not incorporate any notion of genetic linkage, allowing alleles to be inherited completely independently, which would lead to unrealistic rates of allele segregation and

selection, but should not greatly affect the conclusions we draw here. More importantly, the model is lacking several layers of network complexity: notably there are no ‘regulatory genes’,

and the metabolic model similarly lacks any feedback loops or metabolic regulation. These deficiencies should not alter the main concepts and conclusions demonstrated in this study, but may

make it more difficult to apply such models for real-world purposes (such as predicting the levels of heterosis that would be obtained in specific crosses, or predicting ideal selection

pathways to obtain inbreds for maximising heterosis). Nevertheless, we believe that this would be an interesting and rewarding direction to take this research in the future, as promising

results in other studies have been achieved even without the benefit of explicit models of molecular interactions.33 By allowing a system-wide view, computational models provide valuable

insights into complex biological processes or phenomena such as heterosis. Our models provide an approach for rigorously quantifying various contributions to heterosis by different genetic

or metabolic processes. We hope that such models can ultimately be applied to improve the rational design of breeding and selection programs to maximise heterosis for agronomically relevant

traits. METHODS METABOLIC NETWORK AND SIMULATIONS We used the metabolic network of _Arabidopsis thaliana_ presented in ref. 25 The model consists of 549 reactions, 407 metabolites and 6

sub-cellular compartments. The composition and topology of the network were not altered, except for the integration of allele-specific constraints as described below. We used a parsimonious

flux balance analysis (pFBA) to simulate growth in all the experiments. This method uses a two-step optimisation in which the growth rate is optimised using traditional flux balance

analysis, followed by the minimisation of the total flux through all the reactions.34 Minimising the total flux limits the number of possible solutions and improves the predicted flux

distribution by representing an efficient enzyme usage within the network. The original model provides three different biomass compositions: carbon-limiting, nitrogen-limiting, and optimal

growth conditions (under which biomass accumulation is only limited by photon flux into photosynthesis). The latter was systematically used as the objective function in our simulations.

Given the stoichiometric matrix of the network (_S_), flux balance analysis computes the vector of fluxes _v_, using the assumption that the system is at steady state:

$${\mathrm{Maximise}}\quad v_{\mathrm{biomass}} = \mathop {\sum}\nolimits_i {c_iv_i = {c} \cdot {v}}$$ (1) $${\mathrm{subject}}\,{\mathrm{to}}\quad {S} \cdot {v} = 0$$ (2)

$${\mathrm{and}}\quad \alpha _j \le v_j \le \beta _j.$$ (3) In order to minimise the total flux, all the reversible reactions are split into two irreversible reactions, resulting in the

stoichiometric matrix _S_irrev. Thus, each reaction is constrained to carry a positive flux and the total flux is minimised subject to the optimal biomass production rate:

$${\mathrm{Minimize}}\quad \mathop {\sum}\nolimits_j {v_{{\mathrm{irrev}},j}}$$ (4) $${\mathrm{subject}}\,{\mathrm{to}}\quad {S}_{\mathrm{irrev}} \cdot {v}_{\mathrm{irrev}} = 0$$ (5)

$${\mathrm{and}}\quad v_{\mathrm{irrev,biomass}} = v_{\mathrm{biomass}}$$ (6) $${\mathrm{and}}\quad 0 \le v_{{\mathrm{irrev}},j} \le \beta _j.$$ (7) GENERATING ALLELE-SPECIFIC CONSTRAINTS On

the initial parents, metabolic constraints attached to each allele were generated as follows: * (1) First, a pFBA was performed on the original model, resulting in an RFD. The analysis was

set up to maximise the flux through the objective function (biomass) while minimising the sum of all the fluxes in order to limit futile cycles. * (2) FVA was used to compute the maximum and

minimum fluxes for each reaction that maintain a minimum fraction (95%) of the optimum biomass production rate. Alternative FVA minimum fractions (90% and 99%) were also tested, the results

are available in Supplementary Fig. S1. * (3) Each reaction was attributed a pair of alleles (to simulate a diploid organism). In this context, an allele corresponds to a random variable

following the discrete uniform distribution over the set of possible fluxes within the FVA range of a given reaction. * (4) Finally, reactions were constrained by assigning numerical values

their upper or lower bound (depending on the reaction directionality, which was taken from the RFD). Exchange reactions and biomass reactions were left unconstrained in all the simulations.

For all the other reactions, the constraint corresponds to the average of its allele values, normalised such as the sum of the constraints across all loci is equal or lower than the sum of

all the fluxes in the RFD. The normalisation ensures that all the individuals have a similar metabolic capacity. QUANTIFYING HETEROSIS The degree of heterosis of an F1 hybrid was defined as

its biomass production rate divided by the average biomass production of the two parents, that is, mid-parent heterosis. SIMULATED CROSSES To simulate the inheritance of genetic material,

one allele from each parent was randomly selected for each reaction. The new pair of alleles was associated with the corresponding reaction in the resulting network. The reaction bounds were

then constrained and normalised as described previously. SELECTION OVER MULTIPLE GENERATIONS To simulate the effect of selection pressure, individuals were ranked based on their biomass

production rate and the top 5% were selected. These best-performing individuals were then used as parents to produce the following generation. Each generation consisted of 500 individuals.

This process was repeated until the number of desired generations was reached. During the production of these increasingly inbred lines, selfing was prevented (a newly created individual is

the result of a crossing between two distinct parents from the same line). PRODUCTION OF F1 AND F2 HYBRIDS F1 individuals were obtained by randomly sampling 30% of the inbreds from two

independent parental lines and crossing them together until the number of desired F1 hybrids was reached (in general, 500 individuals). The two parents were always from distinct populations;

however, several F1 individuals could come from the same combination of parents. Such siblings will contain different combinations of alleles as the parents are not completely homozygous.

The F2 generation was generated in a similar manner; 30% of the individuals from an F1 population were randomly selected and crossed with each other. In our implementation, an F2 individual

always results from a cross between two distinct F1 parents (no selfing allowed) from the same population. To maximise the diversity of F1 and F2 hybrids, we used all possible combinations

of crosses between our 40 inbred populations, resulting in 780 independent F1 and F2 populations containing 390,000 individuals in each generation. DESIGN AND IMPLEMENTATION OF THE

SIMULATION WORKFLOW The simulation of the metabolism of many individuals over multiple generations requires significant computing resources. To avoid scaling problems, the workflow was

designed for parallel high-performance computing. We used a ‘divide and conquer’ design paradigm to break the computing tasks into single sub-problems corresponding the model optimisations.

The entire workflow was written in Python. The simulations were performed using the COnstraint-Based Reconstruction and Analysis (COBRA) Python package35 and the GNU Linear Programming Kit

(http://www.gnu.org/software/glpk). REPORTING SUMMARY Further information on research design is available in the Nature Research Reporting Summary linked to this article. DATA AVAILABILITY

The scripts required to produce the results presented in this study are available at the following address: https://bitbucket.org/mvacher/heterosis_manuscript. REFERENCES * Darwin, C. _The

effects of cross and self fertilisation in the vegetable kingdom_ (John Murray, London, 1876). * Shull, G. H. The composition of a field of maize. _J. Hered._ 4, 296–301 (1908). Article 

Google Scholar  * Edgerton, M. D. Increasing crop productivity to meet global needs for feed, food, and fuel. _Plant Physiol._ 149, 7–13 (2009). Article  CAS  Google Scholar  * Schnable, P.

S. Progress toward understanding heterosis in crop plants. _Annu. Rev. Plant Biol._ 64, 71–88 (2013). Article  CAS  Google Scholar  * Bruce, A. B. The Mendelian theory of heredity and the

augmentation of vigor. _Science_ 32, 627–628 (1910). Article  CAS  Google Scholar  * East, E. M. Heterosis. _Genetics_ 21, 375–397 (1936). CAS  PubMed  PubMed Central  Google Scholar  *

Jones, D. F. Dominance of linked factors as a means of accounting for heterosis. _Proc. Natl. Acad. Sci. USA_ 3, 310–312 (1917). Article  CAS  Google Scholar  * Birchler, J. A., Auger, D. L.

& Riddle, N. C. In search of the molecular basis of heterosis. _Plant Cell_ 15, 2236–2239 (2003). Article  CAS  Google Scholar  * Chen, Z. J. Genomic and epigenetic insights into the

molecular bases of heterosis. _Nat. Rev. Genet._ 14, 471–482 (2013). Article  CAS  Google Scholar  * Crow, J. F. Alternative hypotheses of hybrid vigor. _Genetics_ 33, 477–487 (1948). CAS 

PubMed  PubMed Central  Google Scholar  * Lippman, Z. B. & Zamir, D. Heterosis: revisiting the magic. _Trends Genet._ 23, 60–66 (2007). Article  CAS  Google Scholar  * Birchler, J. A.,

Yao, H., Chudalayandi, S., Vaiman, D. & Veitia, R. A. Heterosis. _Plant Cell_ 22, 2105–2112 (2010). Article  CAS  Google Scholar  * Fiévet, J. B., Dillmann, C. & de Vienne, D.

Systemic properties of metabolic networks lead to an epistasis-based model for heterosis. _Theor. Appl. Genet._ 120, 463–473 (2010). Article  Google Scholar  * Groszmann, M. et al. Changes

in 24-nt siRNA levels in _Arabidopsis_ hybrids suggest an epigenetic contribution to hybrid vigor. _Proc. Natl. Acad. Sci. USA_ 108, 2617–2622 (2011). Article  CAS  Google Scholar  * Jahnke,

S. et al. Heterosis in early seed development: a comparative study of F1 embryo and endosperm tissues 6 days after fertilization. _Theor. Appl. Genet._ 120, 389–400 (2010). Article  Google

Scholar  * Li, Z. et al. Overdominant epistatic loci are the primary genetic basis of inbreeding depression and heterosis in rice. I. Biomass and grain yield. _Genetics_ 158, 1737–1753

(2001). CAS  PubMed  PubMed Central  Google Scholar  * Mohayeji, M. et al. Heterosis profile of sunflower leaves: a label free proteomics approach. _J. Proteomics_ 99, 101–110 (2014).

Article  CAS  Google Scholar  * Shapira, R., Levy, T., Shaked, S., Fridman, E. & David, L. Extensive heterosis in growth of yeast hybrids is explained by a combination of genetic models.

_Heredity_ 113, 316–326 (2014). Article  CAS  Google Scholar  * Swanson-Wagner, R. A. et al. All possible modes of gene action are observed in a global comparison of gene expression in a

maize F1 hybrid and its inbred parents. _Proc. Natl. Acad. Sci. USA_ 103, 6805–6810 (2006). Article  CAS  Google Scholar  * Wang, Z., Xue, Z. & Wang, T. Differential analysis of

proteomes and metabolomes reveals additively balanced networking for metabolism in maize heterosis. _J. Proteome Res._ 13, 3987–4001 (2014). Article  CAS  Google Scholar  * Wei, G. et al. A

transcriptomic analysis of superhybrid rice LYP9 and its parents. _Proc. Natl. Acad. Sci. USA_ 106, 7695–7701 (2009). Article  CAS  Google Scholar  * Wen, W. et al. Genetic determinants of

the network of primary metabolism and their relationships to plant performance in a maize recombinant inbred line population. _Plant Cell_ 27, 1839–1856 (2015). Article  CAS  Google Scholar

  * Seymour, D. K. et al. Genetic architecture of nonadditive inheritance in _Arabidopsis thaliana_ hybrids. _Proc. Natl. Acad. Sci. USA_ 113, 7317–7326 (2016). Article  Google Scholar  *

Emmrich, P. M., Roberts, H. E. & Pancaldi, V. A. Boolean gene regulatory model of heterosis and speciation. _BMC Evol. Biol._ 15, 24 (2015). Article  Google Scholar  * Arnold, A. &

Nikoloski, Z. Bottom-up metabolic reconstruction of _Arabidopsis_ and its application to determining the metabolic costs of enzyme production. _Plant Physiol._ 165, 1380–1391 (2014). Article

  CAS  Google Scholar  * Mahadevan, R. & Schilling, C. H. The effects of alternate optimal solutions in constraint-based genome-scale metabolic models. _Metab. Eng._ 5, 264–276 (2003).

Article  CAS  Google Scholar  * Larhlimi, A., David, L., Selbig, J. & Bockmayr, A. F2C2: a fast tool for the computation of flux coupling in genome-scale metabolic networks. _BMC

Bioinforma._ 13, 57 (2012). Article  Google Scholar  * Crnokrak, P. & Roff, D. A. Inbreeding depression in the wild. _Heredity_ 83, 260–270 (1999). Article  Google Scholar  * Wright, L.

I., Tregenza, T. & Hosken, D. J. Inbreeding, inbreeding depression and extinction. _Conserv. Genet._ 9, 833–843 (2008). Article  Google Scholar  * Shapira, R. & David, L. Genes with

a combination of over-dominant and epistatic effects underlie heterosis in growth of _Saccharomyces cerevisiae_ at high temperature. _Front. Genet._ 7, 72 (2016). Article  Google Scholar  *

Schnell, F. W. & Cockerham, C. C. Multiplicative vs. arbitrary gene action in heterosis. _Genetics_ 131, 461–469 (1992). CAS  PubMed  PubMed Central  Google Scholar  * Wang, L. et al.

Hybrid mimics and hybrid vigor in _Arabidopsis_. _Proc. Natl. Acad. Sci. USA_ 112, 4959–4967 (2015). Article  Google Scholar  * Riedelsheimer, C. et al. Genomic and metabolic prediction of

complex heterotic traits in hybrid maize. _Nat. Genet._ 44, 217–220 (2012). Article  CAS  Google Scholar  * Lewis, N. E. et al. Omic data from evolved _E. coli_ are consistent with computed

optimal growth from genome‐scale models. _Mol. Syst. Biol._ 6, 390 (2010). Article  Google Scholar  * Ebrahim, A., Lerman, J. A., Palsson, B. O. & Hyduke, D. R. COBRApy:

COnstraints-Based Reconstruction and Analysis for Python. _BMC Syst. Biol._ 7, 74 (2013). Article  Google Scholar  Download references ACKNOWLEDGEMENTS This work was funded by the Australian

Research Council (Centre of Excellence grant CE140100008). We thank Kevin Stratford for his insightful feedback on the development of the simulation scripts. Computational resources were

provided by the Pawsey Supercomputing Centre (http://www.pawsey.org.au). This work was funded by the Australian Research Council (Centre of Excellence grant CE140100008). AUTHOR INFORMATION

Author notes * Michael Vacher Present address: Australian eHealth Research Centre, Commonwealth Scientific and Industrial Research Organisation, Floreat, WA, 6014, Australia AUTHORS AND

AFFILIATIONS * Australian Research Council Centre of Excellence in Plant Energy Biology, School of Molecular Sciences, The University of Western Australia, Crawley, WA, 6009, Australia

Michael Vacher & Ian Small Authors * Michael Vacher View author publications You can also search for this author inPubMed Google Scholar * Ian Small View author publications You can also

search for this author inPubMed Google Scholar CONTRIBUTIONS I.S. devised the project and the main conceptual ideas. M.V. developed the computational framework, performed the simulations

and data analysis. I.S. and M.V. verified the analytical methods. Both authors contributed substantially to the final manuscript. CORRESPONDING AUTHOR Correspondence to Ian Small. ETHICS

DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in

published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION REPORTING SUMMARY RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are

included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Vacher, M., Small, I. Simulation of heterosis in a genome-scale

metabolic network provides mechanistic explanations for increased biomass production rates in hybrid plants. _npj Syst Biol Appl_ 5, 24 (2019). https://doi.org/10.1038/s41540-019-0101-8

Download citation * Received: 12 November 2018 * Accepted: 28 June 2019 * Published: 18 July 2019 * DOI: https://doi.org/10.1038/s41540-019-0101-8 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative