Reader TTS

ABSTRACT The goal of this work was to develop a mathematical model to predict Kaplan–Meier survival curves for chemotherapy combined with radiation in Non-Small Cell Lung Cancer patients for

use in clinical trial design. The Gompertz model was used to describe tumor growth, radiation effect was simulated by the linear-quadratic model with an _α_/_β_-ratio of 10, and

chemotherapy effect was based on the log-cell kill model. To account for repopulation during treatment, we considered two independent methods: 1) kickoff-repopulation using exponential

growth with a decreased volume doubling time, or 2) Gompertz-repopulation using the gradually accelerating growth rate with tumor shrinkage. The input parameters were independently estimated

by fitting to the SEER database for untreated tumors, RTOG-8808 for radiation only, and RTOG-9410 for sequential chemo-radiation. Applying the model, the benefit from concurrent

chemo-radiation comparing to sequential for stage III patients was predicted to be a 6.6% and 6.2% improvement in overall survival for 3 and 5-years respectively, comparing well to the 5.3%

and 4.5% observed in RTOG-9410. In summary, a mathematical model was developed to model tumor growth over extended periods of time, and can be used for the optimization of combined

chemo-radiation scheduling and sequencing. SIMILAR CONTENT BEING VIEWED BY OTHERS IDENTIFICATION OF OPTIMAL DOSING SCHEDULES OF DACOMITINIB AND OSIMERTINIB FOR A PHASE I/II TRIAL IN ADVANCED

_EGFR_-MUTANT NON-SMALL CELL LUNG CANCER Article Open access 17 June 2021 SURVIVAL OUTCOMES OF PATIENTS WITH METASTATIC NON-SMALL CELL LUNG CANCER RECEIVING CHEMOTHERAPY OR IMMUNOTHERAPY AS

FIRST-LINE IN A REAL-LIFE SETTING Article Open access 13 June 2023 EVALUATION OF SOLID TUMOR RESPONSE TO SEQUENTIAL TREATMENT CYCLES VIA A NEW COMPUTATIONAL HYBRID APPROACH Article Open

access 02 November 2021 INTRODUCTION Non-Small Cell Lung Cancer (NSCLC) is a heterogeneous disease, which not only relates to its anatomical presentation, but also to the diverse biology1.

As 40% of patients with NSCLC have locally advanced unresectable disease, combined chemotherapy and radiotherapy (CRT) is considered to be the first choice therapy for most of them2,3.

Though some gains in Overall Survival (OS) have been achieved over the past decades, long term survival in unresectable stage III NSCLC patients remains low and many efforts have been made

to improve treatment. Mathematical modeling plays an important role for developing hypotheses to be tested in future clinical trials and for optimizing their design. Especially in the area

of accelerated fractionation explored by the CHART and CHARTWEL trials, radiobiological models played a large role in trial design and estimating the therapeutic benefit4. The trend to

stratify patients further into smaller sub-groups and in-treatment adaptation approaches increase the importance of patient-specific modeling in lung cancer. The characterization of the

effect of different treatment regimen is usually limited to the effect of radiation dose5,6, and sometimes include tumor volume7. However, it is well known that the combination and

sequencing of chemotherapy with radiotherapy is playing an important role in the treatment of NSCLC8. There are few efforts to mathematically model these combination therapies, which would

facilitate patient stratification and optimization of sequencing in combined chemoradiotherapy9. In this paper, we develop a mathematical model to predict the Kaplan-Meier survival curve

(KMsc), which is basically a cumulative survival frequency distribution curve, for a NSCLC patient population using a “Top-Bottom” methodology, i.e. using observable patient data as starting

point. The aims are to * I. Develop a NSCLC tumor growth model and patient death model using data of untreated patients, and compare it to clinical observations of tumor size and growth

rates. * II. Derive population distributions of radiation effect parameters using data of radiation-only trials and results from (I). * III. Derive population distributions of chemotherapy

effect parameters using data of sequential chemotherapy-radiation trials and results from (I) and (II). The performance and viability of the model is evaluated and discussed with the

published datasets. METHODS TUMOR GROWTH MODELING Multiple methods of modeling the kinetics of tumor growth have been proposed10,11. One of the most popular models is exponential growth,

which assumes the tumor can grow exponentially without any capacity constraints until the death of the patient. Exponential growth kinetics can describe tumor growth well when the tumor is

relatively small, however, this is not the case for larger tumors considering the insufficient nutrition or vascularity of the tumor11. In order to account for the decreased growth rate with

increased tumor volume, other models, e.g. the logistic and Gompertz model, were proposed. In this paper, we employed Gompertz growth, where the evolution of tumor cell number _N_ (i.e.

volume times cell density) with growth rate ρ is described by the following differential equation: $$\frac{dN(t)}{dt}=\rho N(t){log}(\frac{K}{N(t)})$$ (1) The growth rate \(\rho \) and

carrying capacity \(K\) are the specific parameters determining the growth curve of a tumor. With this methodology, we are able to simulate one Gompertz growth curve for tumors with

different initial volumes (e.g. different stages), enabling us to describe the clinical stages I through IV in one coherent framework. In the Gompertz model, the volume doubling time is

variable and not well defined as in the exponential growth model, where it is constant. In order to compare to data from the literature, we therefore used the same expression for the VDT as

the exponential growth model, which is, $$VDT=(t2-t1)\frac{\mathrm{ln}(2)}{\mathrm{ln}(\frac{{v}_{t2}}{{v}_{t1}}\,)}$$ (2) where t1 is the time of the first examination and t2 is the time of

the second examination, \({v}_{t1}\) and \({v}_{t2}\) is the volume at t1 and t2 respectively. We assumed t2 occurs 1 year after t1 in this paper to compare to the literature values, which

is similar to the observation periods used in most lung screening papers12,13. RADIATION EFFECT MODELING The most commonly used tool for quantitative predictions of radiation effects is the

linear quadratic (LQ) model14,15. The LQ model describes that the number of surviving cells after being irradiated by a certain dose of radiation takes the form of an exponential function

with a linear and a quadratic term. In the typical dose range (under 10 Gy per fraction) and fractionation of clinical interest in stage III NSCLC, the LQ model shows good performance in

terms of describing the radiation effect as a function of prescription dose. The formula can be expressed in differential equation as, $$\frac{dN(t)}{dt}=-(\alpha d(t)+\beta

d{(t)}^{2})N(t)$$ (3) In our approach we assumed \(\alpha /\beta \) = 10, which is consistent with assessments from clinical trials for NSCLC patients16. The cell kill from radiation was

determined by the patient-specific radiosensitivity parameter \({\rm{\alpha }}\) and \({\rm{\alpha }}/{\rm{\beta }}\). Radiosensitivity refers to the relative susceptibility of cells to the

harmful effect of ionizing radiation. Considering that cells with faster growth rate have shown to be more radiation-sensitive17,18,19, we also introduced a possible correlation between

radio-sensitivity \(\alpha \) and the growth rate parameter \(\rho \). CHEMOTHERAPY EFFECT MODELING The log-cell kill model was used to simulate chemotherapy effects. The log-cell kill model

subtracts a certain fraction of cancer cells based on the drug concentration regardless of the tumor size at the time of administration9,20,21. It can be expressed as,

$$\frac{dN(t)}{dt}=-{\beta }_{c}C(t)N(t)$$ (4) where, \({\beta }_{c}\) represents the chemotherapy effect per dose, and \(C(t)\) is the drug concentration at a certain time point. In our

model, the concentration was assumed as an exponential decay process, $${\rm{C}}({\rm{t}})={{\rm{C}}}_{max}{e}^{-\frac{\mathrm{ln}(2)}{halflife}t}$$ (5) KAPLAN-MEIER SURVIVAL CURVE

ESTIMATION DEATH AND TUMOR CONTROL CONDITIONS In the literature the time of death is estimated to be about 41 doubling times, which corresponds to a tumor 13 cm in diameter22. In the present

model, we therefore used the 13 cm diameter as the death condition. Besides the death from disease we implemented a 1.48% survival reduction according to life expectancy tables from the

SEER data to account for unexpected natural death events. To determine whether the tumor was controlled (i.e. no single clonogenic cell survives), we used the Poisson probability

$$p={e}^{(-N(t))}$$ (6) which determines the probability of tumor control given N remaining cells. A random value was then generated between 0 and 1 to determine whether the specific tumor

in the patient is controlled. INITIAL VOLUME For the volume distribution in each stage, a log-normal distribution was assumed, as often seen in clinical patient series23. The range for each

stage was defined based on the AJCC standard criteria24. The maximum of the volume distribution for stage I is 5 cm in diameter. For other stages, the volume can be any size, while it should

be lower than the death condition (i.e. 13 cm). Considering the detection ability of the diagnostic technology, we use a diameter of 0.3 cm as the minimal detectable volume for all

stages25. The tumor cell density was assumed to be 5.8 × 108 per cm3, as determined experimentally for lung cancer26. The choice of the density parameter should not be crucial in our model,

as it simply scales everything in an equal manner and a different choice would not have an impact on the ability of the model to fit clinical data. MONTE CARLO PATIENT POPULATION To obtain a

Kaplan-Meier survival curve, we used a Monte Carlo method to sample an initial patient population, where each patient has specific tumor and treatment properties, and survival time after

treatment should be obtained for each patient. During the sampling process, normal distribution was used for growth and treatment effect parameters. The delay time, which is the time between

diagnosis and the start of the treatment, was uniformly sampled from 2–3 weeks. In the fitting procedure, 10000 patients were sampled in each iteration in order to reduce the uncertainty.

In the prediction studies, the same number as patients on the trial were sampled each time, which was repeated 100 times to estimate the uncertainty stemming from the limited

population-volume of the specific trial. PARAMETER ESTIMATION We expressed the combined growth, chemotherapy and radiotherapy treatment for one patients as,

$$\frac{dN(t)}{dt}=\mathop{\underbrace{\rho N(t){\rm{l}}{\rm{o}}{\rm{g}}(\frac{K}{N(t)})}}\limits_{{\rm{G}}{\rm{r}}{\rm{o}}{\rm{w}}{\rm{t}}{\rm{h}}}-\mathop{\underbrace{{\beta

}_{c}C(t)N(t)}}\limits_{{\rm{C}}{\rm{h}}{\rm{e}}{\rm{m}}{\rm{o}}{\rm{t}}{\rm{h}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{p}}{\rm{y}}}-\mathop{\underbrace{(\alpha d(t)+\beta

d{(t)}^{2})N(t)}}\limits_{{\rm{R}}{\rm{a}}{\rm{d}}{\rm{i}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}}$$ (7) With this formula, we can derive the KMsc for a sampled patient population, that is

for each patient we have the specific initial volume, the growth parameter, and the treatment response parameters. To derive the parameters based on the clinical observed KMsc, we formulized

the cost function as, $$\min \,\sum _{Mo{n}_{i}=1}^{60}{(S{F}_{model}(Mo{n}_{i})-S{F}_{observed}(Mo{n}_{i}))}^{2}$$ (8) where, \({{SF}}_{{model}}({Mo}{n}_{i})\) represent the survival

fraction of patients who can survive longer than \({Mo}{n}_{i}\). The parameter of the model was derived by fitting to the observations from clinical trials, first only the growth term, then

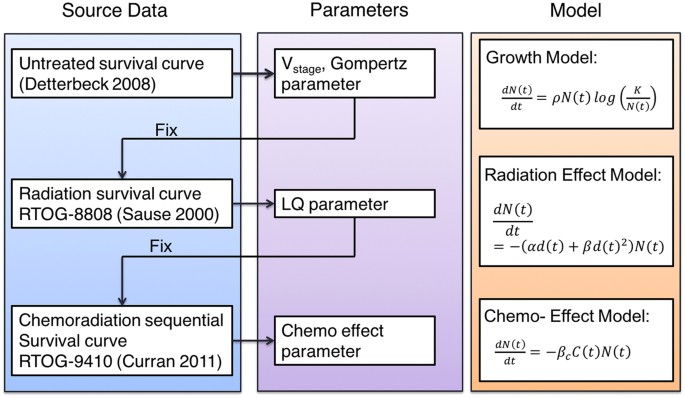
the radiation and chemotherapy terms separately. Consequently, the parameter estimation was a three stage process, as shown in Fig. 1, that is from top to bottom, the previously determined

parameters were fixed and used as input for the next stage. To derive the parameters that determine the tumor volume distribution and the growth pattern, the KMsc were fit to that of an

untreated population collected in Detterbeck _et al_. in 2008 for stage I–IV disease22. The dataset includes the survival of 23954 patients with NSCLC who did not receive surgical resection,

chemotherapy or radiotherapy. With the resulting parameters being fixed we further derived the radiation effect parameter using a radiation-only clinical trial (RTOG 8808), with a

prescribed dose of 60 Gy in 2 Gy fractions27. For the parameters of the chemo-effect model, we used the 60 Gy arm of the RTOG 9410 trial which was designed to compare concurrent and

sequential chemo-radiation therapy8. The enrolled patient numbers is over 200 per arm, prescription includes cisplatin at 100 mg/m3 on days 1 and 29 and vinblastine at 5 mg/m3 per week for 5

weeks. 60 Gy TRT started on day 50 and day 1 for the sequential and concurrent arm respectively. For the two drugs, we used the same \({\beta }_{c}\) for simplicity, with a unit of

(mg/m3)−1. The half-life of the drugs was assumed to be 24 h, as measured in pharmacokinetic studies28,29. Table 1 lists the complete list of the parameters that are used in the model. The

subscripts of \({\rm{\mu }}\) and \({\rm{\sigma }}\) in the table represent the mean and sigma of the distribution for each variable. The optimization was constrained to avoid clearly

implausible combinations of parameter values (as listed in Table 1). For example, the μ and σ for each parameter (including volume, \(\rho \), \(\alpha \) and \({\beta }_{c}\)) can not be

negative, and the minimum detectable tumor diameter is ~3 mm. The model was implemented in python 3.5, for the fit process the lmfit package was applied using Powell’s method. RESULTS AND

DISCUSSION TUMOR GROWTH Based on the survival curve of untreated population, the volume distribution and growth pattern for stage I–IV patients was derived. Considering that this procedure

contains 13-dimensional (i.e. listed under the growth model section in Table 1) parameter space, which cannot be exhaustively explored in a heuristic fashion, we performed a two-stage

optimization procedure to find a sensible and clinically relevant solution (i.e. within the constraints listed in Table 1). In the first stage, we used a pre-defined initial volume

distribution taken from the literature (i.e. Stage I: 2.5 ± 2.5 cm, Stage II: 3.5 ± 3 cm, Stage III:6.6 ± 3 cm) to obtain the optimal parameters (i.e. carrying capacity K and growth

parameter \(\rho \)) for the Gompertz growth model. Figure 2 illustrates the K and \(\rho \) surface with respect to the residuals for \({\rho }_{\mu }\) = 7 \(\times \) 10−5, revealing a

valley with a minimum at K = 30 and \({\rho }_{\sigma }\) = 7.23 \(\times \) 10−3. In the second step we kept these optimal parameters (i.e. K and \(\rho \)) for the Gompertz growth model

constant and re-optimized (i.e. finding the ones resulting in the minimal residual of the cost function) the initial volume distribution that was kept constant before. Figure 3 shows the

predicted Kaplan-Meier survival curves (KMsc) for the untreated populations for different stages together with the observed data. With the fitted initial volume distribution and the growth

parameters (K and \(\rho \)), we obtained the distribution of volume doubling time (VDT) (based on equation 2) for patient populations of each stage during the first year after diagnosis.

The one year interval was chosen because it is commonly used in most lung screening papers12,13. Table 2 lists the tumor volume distributions as predicted by the model fit for the median

tumor diameter for stage I/II/III/IV, i.e. 1.2/3.5/6.9/9.7 cm, respectively. As an example, Figure 4 shows the volume and volume doubling time distributions for stage I patients. The values

for stages I–III are close to observations from studies based on CT or radiographic imaging23,30. The estimated capacity is 30 cm in diameter, which has to be interpreted as a parameter to

describe the slowing growth with increased tumor size, and not as a size to be reached or a realistic volume limit. Similarly, for the stage IV patients, the tumor volume here should not be

interpreted as the solid volume of the primary tumor, but potentially multiple tumor nodules and metastases, and is more a description of “tumor load” in the entire patient. The median value

of VDTs for the tumor were predicted to be 59/89/198/311 days for stage I/II/III/IV, which compares well to literature values12 , 31 even though deviations can be expected due to the

dependence on the time interval32. For example, the mean VDT is between 93–452 days according to several publications12,31,33,34,35,36. The exponential growth model was also implemented for

comparison but resulted in about 40% lower median tumor volumes in stage III patients, not comparing well with the published data (e.g. i.e. Stage I: 2.5 ± 2.5 cm, Stage II: 3.5 ± 3 cm,

Stage III:6.6 ± 3 cm)22,31 and not in line with published GTV (gross tumor volume) sizes at this stage37,38,39. Furthermore, the VDT is a constant of 80 days for all stages, which does not

agree well with the literature especially for later stages (>100 days)12 and is not in agreement with the clinical findings that smaller tumors have a shorter VDT40. RADIATION THERAPY The

radiation therapy response was modeled with the LQ model. Based on experimental observations, a correlation between the growth rate \(\rho \) and the radiosensitivity \(\alpha \) was

considered. The underlying biological interpretation is that faster growing tumor cells spend a higher proportion of their time in mitosis, which impairs double strand break (DSB) repair and

makes them more radiosensitive compared to slower growing ones17,18,19. In the Small-Cell variant of lung cancer this has also been shown _in-vivo_, as the growth rate measured by Ki-67 in

patient samples correlated with the extent of volumetric response to CRT19. Figure 5 shows the distributions for \(\alpha \) and \(\rho \) on the left, and the survival fraction (i.e.

fraction of cells retaining their reproductive integrity) distribution on the right. The survival fraction in Fig. 5c was obtained based on the LQ model from the derived \(\alpha \)

distribution. As shown in Fig. 5b, the best fit is gained by assuming a slight correlation (coefficient = 0.87) between a patient’s growth rate and radiosensitvity. Figure 5b demonstrates

the superior fit (i.e. lower residual value of the cost function) of the survival curve with correlation comparing to without correlation. The estimated median values for \(\alpha \) for the

radiation effect was 0.16 Gy−1, which is similar to previous _in vivo_ estimates of 0.16–0.1841. These estimated values for \(\alpha \) are below the common range of _in vitro_ estimates

(0.2–0.5 Gy−1)16,42,43. Figure 5c shows the distribution of SF2Gy (the cell survival fraction after 2 Gy), derived from the distribution of the radiosensitivity parameter \(\alpha \). From

clinical observations we know that the growth rate accelerates with the shrinkage of the tumor volume during radiation therapy, a phenomenon termed repopulation44,45. To account for this

effect, most of the current models use the kickoff-repopulation approach, which introduces an exponential growth with a VDT of 3 days after a kick-off period of 28 days, counting from the

start of therapy16. However, this phenomenon is in principle intrinsically included in the Gompertz model, as tumors shrinking from radiation cell kill grow faster according to Gompertz

kinetics. We compared the two approaches in this study. Figure 6 shows the results for the two methods. We found that both repopulation methods can describe the survival curve after

radiation therapy well (see Fig. 6a). This confirms that the parameter-less Gompertz-repopulation can naturally account for repopulation (i.e. gradually decreased VDT as the tumor shrinks,

see Fig. 6c) during radiation therapy. The estimated median values for the radiation effect \(\alpha \) were 0.16 for Gompertz repopulation and 0.17 for kickoff-repopulation respectively.

These values agree well with clinical findings46,47, and underscore that Gompertz growth could naturally account for repopulation without additional parameters. Currently the exponential

growth model is still the standard in radiotherapy effect modeling, evidenced for instance by the inclusion of an exponential growth based time factor in the BED model15,16. Sachs _et al_.

described a similar model, and discussed that simple approaches such as the Gompertz growth and linear-quadratic models can still capture the complicated interactions present during

radiation therapy48. The model described by Sachs _et al_. is similar with the present model. In a recent study, Jeong (2017) developed a mechanistic mathematical model for radiation

therapy, which quantitatively predicted the differences in response seen in early stage lung cancer across the range of clinical dose and fractionation schemes49. They used a compartmental

‘tumourlet’-response model to account for the oxygen and tumor repopulation effect, which is more mechanistic and requires more parameters compared to the present model. Models such as this

could be implemented with our chemotherapy and growth models to enable prediction of fractionation effects. CHEMOTHERAPY With consistent parameters for tumor growth and radiation response,

we then proceeded to derive the chemo-effect parameter \({{\rm{\alpha }}}_{\mathrm{chemo}}\) using the sequential chemo-radiation (sCRT) arm of RTOG 9410. The sCRT included cisplatin at 100 

mg/m3 on days 1 and 29 and vinblastine at 5 mg/m3 per week for 5 weeks with 60 Gy radiation therapy beginning on day 50, as shown in Figure. 7. To explain the observed improvement in

survival of sCRT compared to radiation only, the resulting median chemotherapy effect parameter \({{\rm{\beta }}}_{{\rm{c}}}\) was determined to be 0.028/(mg/ml). As our methodology has not

been used before to derive quantitative cell kill parameters for chemotherapy agents, we verified the predictive power using published data. From published data of large cohorts, we know

that with doublet chemotherapy in stage IV lung cancer patients, the median survival is about 6–10 months and 1-year OS is about 25–35%50,51,52. To test if our model would predict similar

values, we generated cohorts of stage IV patients which received 4 cycles, which is the median number of cycles given51,52, of our chemotherapy simulation and predicted the improvement in

survival. Our model predicted a median survival of 10.2 months, which is reasonably close to the observed survival. The Gompertz model also explains the moderate repopulation (i.e.

accelerated tumor growth) observed after the chemotherapy segment of sequential chemo-radiation, which was observed in clinical trials40,53. Our model predicted a median VDT of 12 days and a

mean VDT of 41 days for a time interval of 100 days between two examinations after induction chemotherapy. Sharouni _et al_. measured the median and mean VDT of 29.4 and 45.8 days after

induction chemotherapy, which they described as significantly lower than the normal VDT40. Also they found that small tumors have the shortest VDTs. This is a confirmation of the results

given by our model. COMBINED MODALITY TREATMENT We simulated concurrent chemo-radiation (cCRT) by combining the parameters obtained above. We took the same chemo- and radiotherapy cell kill

used in Fig. 7a for sCRT and shifted the RT section to start together with the first cycle of chemotherapy, mimicking the concurrent trial arm of RTOG-9410 (see Fig. 7b). The main goal was

to determine if an additional radiosensitization parameter would be necessary to fit the observed survival curves, or if the increased cell kill in a shorter treatment time is sufficient to

explain the superior clinical results of cCRT. Figure 7c demonstrates that the combination of chemotherapy and radiotherapy in a concurrent fashion predicts OS improvements of 6.6% and 6.2%

for 3 and 5-years for stage III patients, which compares well to the 5.3% and 4.5% observed in the cCRT arm (see Fig. 7d) of RTOG-94108. For the overall survival prediction of concurrent and

sequential CRT, our model performs well and predicts results observed in clinical trials (see Fig. 7). There is no need to add a radiosensitization parameter for the interaction between

chemo- and radio-therapy, indicating that the reduction in treatment time and the resulting suppression of repopulation is the deciding factor for the superiority of cCRT compared to sCRT.

Figure 8 demonstrates tumor cell load of a patient who will benefit from the concurrent compared to the sequential chemo-radiation regimen. With sCRT the tumor grows back after chemo- and

radiotherapy, as the cell kill was not dense enough and allowed the tumor to re-grow. Since the tumor cell number was reduced to below 1 (high probability of tumor control) with Concurrent

chemo-radiation therapy, the tumor is controlled according to our model. GROWTH RATE BASED STRATIFICATION OF CONCURRENT AND SEQUENTIAL CRT: AN EXAMPLE APPLICATION To demonstrate the

application of the developed model in clinical practice, we investigated which population benefits most from concurrent chemo-radiation. For most patients who have unresectable disease,

combined chemo and radiation therapy is considered as the first treatment of choice. However, it is unknown how to define criteria for selecting a subgroup of patients who would benefit from

concurrent CRT compared to treating sequentially, which is predicted to cause less toxicity. We separated the patient population into subgroups according to the growth rate distribution

(considering the median of the distribution and the growth parameter \({\rm{\rho }}\)). All parameters for treatment response are given in Table 3. The schedule of combined chemotherapy and

radiation treatment was set as identical to RTOG 9410. The model predicted that for patients with a faster tumor growth (above the median), the benefit can be as high as 11.1% for stage III

patients, but only 4.7% for those patients with a slower growth rate (below the median) for 3 year overall survival. The benefit can be as high as 14.4% for patients with a growth rate in

the top 25th percentile. This could be important in the design of clinical trials evaluating treatment options for older and frail patients that cannot tolerate a concurrent regimen,

verifying these predictions in patients might necessitate advanced imaging modalities (e.g. PET-MTV (PET derived metabolic tumor volume)) to determine the growth rate (e.g. utilizing the

correlation between PET-MTV and tumor growth rate55). LIMITATIONS AND FUTURE DIRECTIONS There are numerous models that describe tumor growth and treatment response. However, none of the

standard models allows simulation and prediction of multi-modality regimen for locally-advanced NSCLC. We developed a mathematical model for the combined treatment of chemotherapy and

radiation based on overall survival data from several clinical trials, with the purpose of improving and optimizing treatment strategies for future clinical trials. Notably, parameters in

the model were derived from the clinical relevant outcome data. The tumor growth and patient death model can also be used as foundation for the simulation of other therapeutic interventions,

such as targeted agents. As every model has its inherent limitations, we would like to highlight the caveats of our approach. * (1) The \({\rm{\alpha }}/{\rm{\beta }}\) -ratio used was 10

and the cell cycle effect and oxygen enhancement ratio for radiosensitivity was not considered. This might be necessary if one wants to investigate different fractionation regimen16, which

was not considered in this study. * (2) The Gompertz model in use was shown to fit the data and clinical observations better than the exponential model. However, there are other models with

the same growth pattern, e.g. the logistic or the Bertalanffy model, which could be expected to have a similar modeling performance11. * (3) Log-cell kill was used to model chemotherapy in

the study, which is commonly used and a widely accepted approach. However, there is another main model in use for this purpose, the Norton-Simons model, which differs significantly56. We do

not think this has an impact on the results of our study, as we investigate only one chemotherapy regimen and only study changes in timing between chemo- and radiotherapy. If the aim would

be to investigate different chemotherapy regimen and their interaction with radiation, then the model in use could have an impact on the results. * (4) There is no modeling of normal tissue

toxicity, although natural deaths were considered. Toxicity from treatment can result in extra deaths, and RTOG 061757, which showed lower survival for the higher dose arm, has raised

questions about the limits of dose escalation with concurrent CRT in the general NSCLC population. Whatever the exact reasons for the lower survival in this trial may be, toxicity might play

a prominent role. Therefore models such as the one presented above should be used with care for regimen that are supposedly pushing the boundaries of normal tissue toxicity. However, a

toxicity component could be added to the current model, which would necessitate the analysis of dose distributions for all patients, which were unavailable for these trials. CONCLUSION

Combined CRT is a mainstay of treatment for locally-advanced NSCLC patients. We developed a mathematical model for the combined treatment of chemotherapy and radiation, with the purpose of

improving and optimizing treatment strategies for future clinical trials. The established model can predict survival curves for populations of NSCLC patients with or without treatment. The

parameter-less Gompertz repopulation can naturally account for repopulation during radiation therapy and after induction chemotherapy. The model provides a tool for the optimization of

combined chemo-radiation scheduling and sequencing. CHANGE HISTORY * _ 17 AUGUST 2018 A correction to this article has been published and is linked from the HTML and PDF versions of this

paper. The error has not been fixed in the paper. _ REFERENCES * Chen, Z., Fillmore, C. M., Hammerman, P. S., Kim, C. F. & Wong, K.-K. Non-small-cell lung cancers: a heterogeneous set of

diseases. _Nature Reviews Cancer_ 15, 247–247 (2015). Article  CAS  Google Scholar  * Dincklage, von,J. J., Ball, D. & Silvestri, G. A. A review of clinical practice guidelines for lung

cancer. _Journal of Thoracic Disease_ 5, S607–S622 (2013). Google Scholar  * Johnson, D. H. Locally Advanced, Unresectable Non-Small Cell Lung Cancer: New Treatment Strategies. _CHEST_ 117,

123S–126S (2000). Article  PubMed  CAS  Google Scholar  * Bentzen, S. M., Saunders, M. I. & Dische, S. From CHART to CHARTWEL in Non-small Cell Lung Cancer: Clinical Radiobiological

Modelling of the Expected Change in Outcome. _Clinical Oncology_ 14, 372–381 (2002). Article  PubMed  CAS  Google Scholar  * Kong, F.-M., Haken, R. T., Eisbruch, A. & Lawrence, T. S.

Non-Small Cell Lung Cancer Therapy-Related Pulmonary Toxicity: An Update on Radiation Pneumonitis and Fibrosis. _Seminars in Oncology_ 32, 42–54 (2005). Article  CAS  Google Scholar  *

Rosenzweig, K. E. _et al_. Results of a phase I dose‐escalation study using three‐dimensional conformal radiotherapy in the treatment of inoperable nonsmall cell lung carcinoma. _Cancer_

103, 2118–2127 (2005). Article  PubMed  Google Scholar  * Willner, J., Baier, K., Caragiani, E., Tschammler, A. & Flentje, M. Dose, volume, and tumor control prediction in primary

radiotherapy of non-small-cell lung cancer. _International Journal of Radiation Oncology*Biology*Physics_ 52, 382–389 (2002). Article  Google Scholar  * Curran, W. J. _et al_. Sequential vs

Concurrent Chemoradiation for Stage III Non-Small Cell Lung Cancer: Randomized Phase III Trial RTOG 9410. _JNCI Journal of the National Cancer Institute_ 103, 1452–1460 (2011). Article 

PubMed  PubMed Central  CAS  Google Scholar  * Grassberger, C. & Paganetti, H. Methodologies in the modeling of combined chemo-radiation treatments. Physics in Medicine & Biology

344–369, https://doi.org/10.1088/0031-9155/61/21/R344 (2016). * Benzekry, S. _et al_. Classical Mathematical Models for Description and Prediction of Experimental Tumor Growth. _PLoS Comput

Biol_ 10, e1003800–20 (2014). Article  PubMed  PubMed Central  CAS  Google Scholar  * Gerlee, P. The Model Muddle: In Search of Tumor Growth Laws. _Cancer Research_ 73, 2407–2411 (2013).

Article  PubMed  CAS  Google Scholar  * Usuda, K., Saito, Y., Sagawa, M. & Sato, M. Tumor doubling time and prognostic assessment of patients with primary lung cancer. _Cancer_ 74,

2239–2244 (1994). Article  PubMed  CAS  Google Scholar  * Yankelevitz, D. F. _et al_. Overdiagnosis in chest radiographic screening for lung carcinoma. _Cancer_ 97, 1271–1275 (2003). Article

  PubMed  Google Scholar  * Brenner, D. J. The Linear-Quadratic Model Is an Appropriate Methodology for Determining Isoeffective Doses at Large Doses Per Fraction. _Seminars in Radiation

Oncology_ 18, 234–239 (2008). Article  PubMed  PubMed Central  Google Scholar  * Fowler, J. F. 21 years of Biologically Effective Dose. _BJR_ 83, 554–568 (2010). Article  PubMed  CAS  Google

Scholar  * Mehta, M. _et al_. A new approach to dose escalation in non–small-cell lung cancer. _Radiation Oncology Biology_ 49, 23–33 (2001). Article  CAS  Google Scholar  * Lee, J. Y.,

Kim, M.-S., Kim, E. H., Chung, N. & Jeong, Y. K. Retrospective growth kinetics and radiosensitivity analysis of various human xenograft models. _Lab Anim Res_ 32, 187–7 (2016). Article 

PubMed  PubMed Central  Google Scholar  * Shibamoto, Y. _et al_. Proliferative activity and micronucleus frequency after radiation of lung cancer cells as assessed by the cytokinesis-block

method and their relationship to clinical outcome. _Clinical Cancer Research_ 4, 677–682 (1998). PubMed  CAS  Google Scholar  * Ishibashi, N. _et al_. Correlation between the Ki-67

proliferation index and response to radiation therapy in small cell lung cancer. _Radiation Oncology 2017_ 12(12:1), 16 (2017). Article  CAS  Google Scholar  * Skipper, H. E. Perspectives in

Cancer Chemotherapy: Therapeutic Design. _Cancer Research_ 24, 1295–1302 (1964). PubMed  CAS  Google Scholar  * Powathil, G., Kohandel, M., Sivaloganathan, S., Oza, A. & Milosevic, M.

Mathematical modeling of brain tumors: effects of radiotherapy and chemotherapy. _Physics in Medicine & Biology_ 52, 3291–3306 (2007). Article  CAS  Google Scholar  * Detterbeck, F. C.

& Gibson, C. J. Turning Gray: The Natural History of Lung Cancer Over Time. _Journal of Thoracic Oncology_ 3, 781–792 (2008). Article  PubMed  Google Scholar  * Wisnivesky, J. P.,

Yankelevitz, D. & Henschke, C. I. The Effect of Tumor Size on Curability of Stage I Non-small Cell Lung Cancers. _CHEST_ 126, 761–765 (2004). Article  PubMed  Google Scholar  * Edge, S.

B. & Compton, C. C. The American Joint Committee on Cancer: the7th Edition of the AJCC Cancer Staging Manual and the Future of TNM. _Ann Surg Oncol_ 17, 1471–1474 (2010). Article  PubMed

  Google Scholar  * Winer-Muram, H. T. _et al_. Volumetric Growth Rate of Stage I Lung Cancer prior to Treatment: Serial CT Scanning. _Radiology_ 223, 798–805 (2002). Article  PubMed  Google

Scholar  * Switzer, P., Gerstl, B. & Greenspoon, J. Karyometry in the Estimation of Nuclear Population in Pulmonary Carcinomas. _JNCI Journal of the National Cancer Institute_ 52,

1699–1704 (1974). Article  PubMed  CAS  Google Scholar  * Sause, W. _et al_. Final Results of Phase III Trial in Regionally Advanced Unresectable Non-Small Cell Lung Cancer: Radiation

Therapy Oncology Group, Eastern Cooperative Oncology Group, and Southwest Oncology Group. _CHEST_ 117, 358–364 (2000). Article  PubMed  CAS  Google Scholar  * Saeb-Parsy, K. _Instant

Pharmacology_. (John Wiley & Sons, 1999). * Kumar, A. Vincristine and Vinblastine: A Review. _IJMPS_ 6, 23–30 (2016). CAS  Google Scholar  * Martini, N. _et al_. Survival after resection

of stage II non-small cell lung cancer. _The Annals of Thoracic Surgery_ 54, 460–466 (1992). Article  PubMed  CAS  Google Scholar  * Geddes, D. M. The natural history of lung cancer: A

review based on rates of tumour growth. _British Journal of Diseases of the Chest_ 73, 1–17 (1979). Article  PubMed  CAS  Google Scholar  * Mehrara, E., Forssell-Aronsson, E., Ahlman, H.

& Bernhardt, P. Specific Growth Rate versus Doubling Time for Quantitative Characterization of Tumor Growth Rate. _Cancer Research_ 67, 3970–3975 (2007). Article  PubMed  CAS  Google

Scholar  * Hasegawa, M. _et al_. Growth rate of small lung cancers detected on mass CTscreening. _BJR_ 73, 1252–1259 (2014). Article  Google Scholar  * Steel, G. G. _The growth Kinetics of

Tumours_. (Oxford University Press, 1977). * Fujimura, S., Suda, S., Yamauchi, A., Sato, H. & Sohara, Y. Tumor doubling time and PPD skin test reactivity in resectable lung cancer. _J

Jpn Lung Cancer Soc_ 19, 135–142 (1978). Article  Google Scholar  * Filderman, A. E., Shaw, C. & Matthay, R. A. Lung Cancer: Part I: Etiology, Pathology, Natural History, Manifestations,

and Diagnostic Techniques. _Investigative Radiology_ 21, 80 (1986). Article  PubMed  CAS  Google Scholar  * Fox, J. _et al_. Quantification of Tumor Volume Changes During Radiotherapy for

Non–Small-CellLung Cancer. _International Journal of Radiation Oncology*Biology*Physics_ 74, 341–348 (2009). Article  Google Scholar  * Basaki, K. _et al_. Prognostic factors for survival in

stage III non–small-cell lung cancer treated with definitive radiation therapy: Impact of tumor volume. _International Journal of Radiation Oncology*Biology*Physics_ 64, 449–454 (2006).

Article  Google Scholar  * Kozak, M. M. _et al_. Tumor Volume as a Potential Imaging-Based Risk-Stratification Factor in Trimodality Therapy for Locally Advanced Non-small Cell Lung Cancer.

_Journal of Thoracic Oncology_ 6, 920–926 (2011). Article  PubMed  Google Scholar  * Sharouni, E, S. Y., Kal, H. B. & Battermann, J. J. Accelerated regrowth of non-small-cell lung

tumours after induction chemotherapy. 89, 2184–2189 (2003). * Liu, F. _et al_. Tumor control probability modeling for stereotactic body radiation therapy of early-stage lung cancer using

multiple bio-physical models. _Radiotherapy and Oncology_ 122, 286–294 (2017). Article  PubMed  Google Scholar  * Franken, N., Hovingh, S. & Rodermond, H. Radiosensitization with

chemotherapeutic agents and hyperthermia: Effects on linear-quadratic parameters of radiation cell survival curves. _J Cancer Sci_ Ther (2011). * Ohri, N., Dicker, A. P. & Lawrence, Y.

R. Can Drugs Enhance Hypofractionated Radiotherapy? A Novel Method of Modeling Radiosensitization Using _In Vitro_ Data. _International Journal of Radiation Oncology*Biology*Physics_ 83,

385–393 (2012). Article  CAS  Google Scholar  * Shafiq, J., Hanna, T. P., Vinod, S. K., Delaney, G. P. & Barton, M. B. A Population-based Model of Local Control and Survival Benefit of

Radiotherapy for Lung Cancer. _Clinical Oncology_ 28, 627–638 (2016). Article  PubMed  CAS  Google Scholar  * Kim, J. J. & Tannock, I. F. Repopulation of cancer cells during therapy: an

important cause of treatment failure. _Nature Reviews Cancer_ 5, 516–525 (2005). Article  PubMed  CAS  Google Scholar  * Zhong, H. & Chetty, I. A note on modeling of tumor regression for

estimation of radiobiological parameters. _Med. Phys._ 41, 081702 (2014). Article  PubMed  PubMed Central  Google Scholar  * Hedman, M., Björk-Eriksson, T., Brodin, O. & Toma-Dasu, I.

Predictive value of modelled tumour control probability based on individual measurements of _in vitro_ radiosensitivity and potential doubling time. _BJR_ 86, 20130015 (2014). Article 

Google Scholar  * Sachs, R. K., Hlatky, L. R. & Hahnfeldt, P. Simple ODE models of tumor growth and anti-angiogenic or radiation treatment. _Mathematical and Computer Modelling_ 33,

1297–1305 (2001). Article  MathSciNet  MATH  Google Scholar  * Jeong, J. _et al_. Modeling the Cellular Response of Lung Cancer to Radiation Therapy for a Broad Range of Fractionation

Schedules. _Clinical Cancer Research_ clincanres.3277, https://doi.org/10.1158/1078-0432.CCR-16-3277 (2017). * Booton, R. _et al_. A phase III trial of docetaxel/carboplatin versus mitomycin

C/ifosfamide/cisplatin (MIC) or mitomycin C/vinblastine/cisplatin (MVP) in patients with advanced non-small-cell lung cancer: a randomised multicentre trial of the British Thoracic Oncology

Group (BTOG1). _Ann Oncol_ 17, 1111–1119 (2006). Article  PubMed  CAS  Google Scholar  * Johnson, D. H. Evolution of Cisplatin-Based Chemotherapy in Non-Small Cell Lung Cancer: A Historical

Perspective and The Eastern Cooperative Oncology Group Experience. _CHEST_ 117, 133S–137S (2000). Article  PubMed  CAS  Google Scholar  * Wozniak, A. J. _et al_. Randomized trial comparing

cisplatin with cisplatin plus vinorelbine in the treatment of advanced non-small-cell lung cancer: a Southwest Oncology Group study. _JCO_ 16, 2459–2465 (1998). Article  CAS  Google Scholar

  * Chen, C. P., Weinberg, V. K., Jahan, T. M., Jablons, D. M. & Yom, S. S. Implications of Delayed Initiation of Radiotherapy: Accelerated Repopulation after Induction Chemotherapy for

Stage III Non-small Cell Lung Cancer. _Journal of Thoracic Oncology_ 6, 1857–1864 (2011). Article  PubMed  Google Scholar  * Aupérin, A. _et al_. Meta-Analysis of Concomitant Versus

Sequential Radiochemotherapy in Locally Advanced Non–Small-CellLung Cancer. _JCO_ 28, 2181–2190 (2010). Article  CAS  Google Scholar  * Wang, J., Mahasittiwat, P., Wong, K. K., Quint, L. E.

& Kong, F.-M. S. Natural growth and disease progression of non-small cell lung cancer evaluated with 18F-fluorodeoxyglucose PET/CT. _Lung Cancer_ 78, 51–56 (2012). Article  PubMed 

PubMed Central  Google Scholar  * Simon, R. & Norton, L. The Norton–Simon hypothesis: designing more effective and less toxic chemotherapeutic regimens. _Nature Clinical Practice

Oncology_ 3, 406–407 (2006). Article  PubMed  Google Scholar  * Bradley, J. D. _et al_. Standard-dose versus high-dose conformal radiotherapy with concurrent and consolidation carboplatin

plus paclitaxel with or without cetuximab for patients with stage IIIA or IIIB non-small-cell lung cancer (RTOG 0617): a randomised, two-by-two factorial phase 3 study. _The Lancet Oncology_

16, 187–199 (2015). Article  PubMed  PubMed Central  CAS  Google Scholar  Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Radiation Oncology, Massachusetts

General Hospital, Harvard Medical School, 30 Fruit Street, Boston, MA, 02114, USA Changran Geng, Harald Paganetti & Clemens Grassberger * Department of Nuclear Science and Engineering,

Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, People’s Republic of China Changran Geng Authors * Changran Geng View author publications You can also search for this

author inPubMed Google Scholar * Harald Paganetti View author publications You can also search for this author inPubMed Google Scholar * Clemens Grassberger View author publications You can

also search for this author inPubMed Google Scholar CONTRIBUTIONS C.G. (Changran Geng) and C.G. (Clemens Grassberger) designed and implemented the model, and analysed results. C.G. (Changran

Geng) and C.G. (Clemens Grassberger) wrote the main manuscript text based on the discussion with H.P. C.G. (Clemens Grassberger) and H.P. co-supervised the project; All authors reviewed and

approved the final manuscript. CORRESPONDING AUTHORS Correspondence to Changran Geng or Clemens Grassberger. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare that they have no

competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and

reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes

were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If

material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain

permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Geng, C., Paganetti, H. & Grassberger, C. Prediction of Treatment Response for Combined Chemo- and Radiation Therapy for Non-Small Cell Lung Cancer Patients Using a

Bio-Mathematical Model. _Sci Rep_ 7, 13542 (2017). https://doi.org/10.1038/s41598-017-13646-z Download citation * Received: 08 May 2017 * Accepted: 19 September 2017 * Published: 19 October

2017 * DOI: https://doi.org/10.1038/s41598-017-13646-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable

link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative