Reader TTS

ABSTRACT Walking on a beam is a challenging motor skill that requires the regulation of upright balance and stability. The difficulty in beam walking results from the reduced base of support

compared to that afforded by flat ground. One strategy to maintain stability and hence avoid falling off the beam is to rotate the limb segments to control the body’s angular momentum. The

aim of this study was to examine the coordination of the angular momentum variations during beam walking. We recorded movement kinematics of participants walking on a narrow beam and

computed the angular momentum contributions of the body segments with respect to three different axes. Results showed that, despite considerable variability in the movement kinematics, the

angular momentum was characterized by a low-dimensional organization based on a small number of segmental coordination patterns. When the angular momentum was computed with respect to the

beam axis, the largest fraction of its variation was accounted for by the trunk segment. This simple organization was robust and invariant across all participants. These findings support the

hypothesis that control strategies for complex balancing tasks might be easier to understand by investigating angular momentum instead of the segmental kinematics. SIMILAR CONTENT BEING

VIEWED BY OTHERS REGULATION OF WHOLE-BODY ANGULAR MOMENTUM DURING HUMAN WALKING Article Open access 17 May 2023 AGE RELATED DIFFERENCES IN WHOLE BODY AND BODY PART ANGULAR MOMENTUM IN THE

FRONTAL PLANE DURING WALKING Article Open access 26 October 2024 A BIOMECHANICAL STUDY OF LOAD CARRIAGE BY TWO PAIRED SUBJECTS IN RESPONSE TO INCREASED LOAD MASS Article Open access 23

February 2021 INTRODUCTION Walking on a narrow beam is a demanding motor skill that requires the control of dynamic stability, defined as the ability to reduce self-initiated or external

perturbations via inherent restoring moments to avoid loss of balance. Due to the reduced base of support of the beam and the intrinsic variability of the human, walking tends to become

unstable in the medio-lateral (ML) direction1. Walking on a beam has been investigated in multiple studies over the last two decades. For instance, several studies examined the effects of

age on balance control2, the effects of physical guidance on motor learning3 and the neural activation associated with loss of balance control4. More recently, Sawers and colleagues used

beam walking as an experimental paradigm to investigate how long-term training affects muscle synergies5 and how individual differences in proficiency may inform therapists about clinical

problems6. It is important to note that in all these studies, participants were asked to fold their arms in front of the body to isolate “locomotor balance” from the complex arm movements

typically employed to assist balance control. Hof suggested that for a standing human only 3 mechanisms are available for the control of dynamic balance7,8: (1) the shift of the

center-of-pressure under the feet with respect to the vertical projection of the center-of-mass (COM), (2) the rotation of the body segments to counterbalance the variations of the angular

momentum (AM), and (3) the application of external forces. The first strategy has been usually referred to also as “ankle strategy”9, while the second one comprises the “hip strategy”9, i.e.

rotation of the upper body segments around the ankle or hip joint, respectively. These mechanisms can also be exploited to maintain balance in the ML direction when walking on a narrow

beam, although shifting the center-of-pressure under the feet becomes a relatively ineffective balancing strategy, as the beam has a limited width. If holding onto an external object to

apply an external force is not possible, rotating the body segments to create compensatory angular momenta remains the only effective strategy. A systematic investigation of the angular

momentum during beam walking thus might provide deeper insights into the control strategies in such challenging balancing tasks. The angular momentum is a physical quantity that

characterizes the rotational inertia of an object or a system of objects about an axis. In any inertial reference frame, the AM of a system is a conserved quantity as long as no external

forces or torques act on the object. This is the consequence of Euler’s dynamic laws of motion, according to which the derivative of AM is equal to the external torques applied to the

body10. During walking, however, ground reaction forces are constantly acting on the feet, inducing considerable variations of the AM that need to be controlled11. Multiple studies in

biomechanics and motor control have examined the AM to characterize the mechanisms underlying locomotion and balance control11,12,13,14,15. These studies have inspired the design of robust

motion generation policies for robots and computer graphics applications16,17,18,19. Importantly, the AM is computed with respect to an axis about which the object rotates in space,

rendering it a relative measure. In biomechanical studies, it has been common practice to compute the AM with respect to the axis passing through the whole-body center-of-mass. However,

given the complex dynamics of articulated limbs when walking on a beam, it is not a priori guaranteed that this axis is the only or most appropriate choice. The aim of this study was to

investigate the coordination of a complex whole-body movement such as walking on a narrow beam. We collected movement kinematics of 16 healthy participants that were asked to complete 20

successful walks on a very narrow beam placed on the floor. Analyzing the rotations of the body segments projected into the medio-lateral plane, the segmental AM contributions were computed

with respect to 3 different axes: (1) the axis perpendicular to the ML plane through the average center position of the head, (2) the axis perpendicular to the ML plane and passing through

the COM of the whole body, and (3) the axis perpendicular to the ML plane through the center of the beam on the floor. The choice of the axis through the head was motivated by previous

studies that showed that stabilization of the head might be an important control principle for many locomotion tasks20. The long axis of the beam was chosen because the human body can be

seen as an inverted pendulum that rotates about this axis. The analyses of the AM components were confined to rotations in the ML plane with respect to those axes parallel to the walking

direction. Analyses of kinematic variations revealed a very complex structure with large inter-individual differences and no apparent invariances. In contrast, analyses of the AM with

respect to the axis along the beam rendered a very parsimonious description of the observed coordination patterns showing a low-dimensional structure of the AM. These findings suggest that

the underlying control strategy might aim at minimizing the variation of the AM about this axis. RESULTS While walking on the 3.4 cm-wide beam, participants displayed highly variable motor

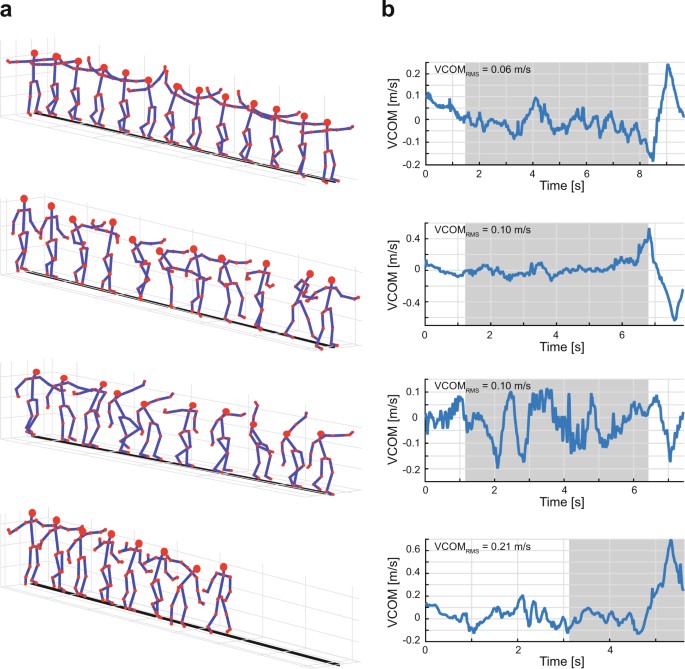
behavior, using a wide range of strategies in order to maintain or regain balance. As an illustration, Figure 1a displays 4 series of body postures that participants adopted during 4 typical

trials; 3 were successful and one was unsuccessful and the participant had to step off the beam. Participants displayed not only large trunk movements, but also large and variable movements

of both arms. When at the brink of falling off the beam, they also abducted their legs. Movies from a set of experimental trials are provided as supplementary material to this article. As

one index to quantify the degree of balance, Figure 1b depicts the time series of the medio-lateral velocity of each of the participants’ whole-body center-of-mass (VCOM). The root mean

square (RMS) of this variable was computed over 15% to 85% of the duration of each successful trial or over the last 3 seconds prior to loosing balance. The interval for this computation is

highlighted in grey in Figure 1b. Comparison of the VCOMRMS for all successful and unsuccessful trials confirmed that the variations in successful trials were significantly smaller, VCOMRMS 

= 0.03 ± 0.01 m/s, than in those trials when participants lost their balance, VCOMRMS = 0.15 ± 0.08 m/s, t139 = −170.6, p < 0.001. The highly variable behavior was also evident in a

principal component analysis (PCA) applied to the relative orientations of the segments. Figure 2a shows the variance accounted for (VAF) for the successful trials as function of the number

of principal components, averaged across 16 participants. The whole-body movements required on average 8 components to account for at least 95% of the variance. After applying a VARIMAX

rotation, we obtained components with average sparsity indexes ranging between 0.65 and 0.91 (Fig. 2b). By definition, the sparsity index is 1 if only one single element of the vector is

different from 0, when more components are non-zero then sparsity is lower than 1 (see Methods for more detail). All components accounted for similar amounts of variance (Fig. 2c). In order

to test whether participants have improved over the 20 trials and changed their strategy, we split the 20 trials in 2 blocks: block 1 comprised the first 10 successful trials, block 2 the

second 10 successful trials. The same PCA was applied to the covariance matrices associated with the 2 blocks. We found that for both blocks 8 components were needed to account for 95% of

the variation associated with the data. Comparing the components of the 2 blocks revealed that they were similar, _S_ = 0.90 ± 0.14. This average similarity index _S_ was quantified as the

dot product between 2 components, normalized with respect to their norms. By definition, the index _S_ is equal to 1 when the components are proportional (see Methods for details). These

results suggested that subjects’ strategy did not change significantly across the duration of the experiment, i.e., there was no sign of learning effects. In order to assess the

inter-individual variations of the kinematic coordination structure, we applied a cross-validation procedure. For this purpose, the principal components of a single participant were used to

predict the data from each of the other participants. The amount of variance explained for all pairwise comparisons was low, the average VAF was 44.05 ± 26.45%, indicating little consistency

between the kinematic strategies of the individual participants. Given this high dimensionality and large inter-individual differences in the kinematics, we proceeded to calculate the

angular momenta of the body segments. While the typical axis used for this calculation is the axis through the whole-body COM, we also calculated AM with respect to 2 additional axes, one

parallel to and through the beam and one through the central position of the head. Figure 3 shows the temporal evolution of the angular momentum through the 3 axes from the trial in the top

panel of Figure 1. While the 3 time series are visibly correlated, they also display considerable differences in amplitude and variability. These qualitative observations were confirmed by

the average correlation coefficients (_R_) and RMS values (LRMS) associated with the angular momenta, which are summarized in Table 1. Applying principal component analysis to the AM

computed with respect to the different axes revealed substantial differences between the segmental coordination patterns. Figure 4a shows the cumulative variance accounted for each of the 3

axes. Before averaging, the principal components associated with different participants were paired and grouped according to their similarity. While 4 or 5 components were required to

account for about 95% VAF for the whole-body COM and the head, the center of the beam as reference axis needed only one single component for a comparable VAF. Figure 4b depicts the first 5

components for the 3 axes after a VARIMAX rotation. There were considerable differences between the 3 axes with respect to the structure of the extracted components. However, the axis

through the beam center showed a particularly simple structure: the first PC was associated mainly with the trunk segment, the second and the third PCs with the left and right arm, and the

fourth and the fifth PCs with the left and right leg. The similarity index _S_ between the components identified with respect to the axis through the head and through the COM was _S_ = 0.80 

± 0.10. Similarly, for the components computed with respect to the head axis and the beam axis, _S_ = 0.60 ± 0.03. For the sets of components associated with the whole-body COM axis and the

beam axis, _S = _0.63 ± 0.07. These moderate values of similarity give evidence that the segmental patterns of covariation were highly dependent on the reference axis chosen for the

computation of the AM. Further, the analysis of the sparseness of the components revealed that the PCs computed with the beam axis were on average sparser than the corresponding PCs for the

other 2 reference axes. This implies that using the beam center as axis rendered the lowest-dimensional description of the underlying signal space. Figure 4c illustrates how the variance was

distributed across the different components. When AM was computed with respect to the head axis, all components accounted for a comparable amount of data variation, with PC1 accounting for

the smallest amount. In contrast, using the COM or the beam as axis, the biggest contribution to data variation came from the first component alone, leaving only a small amount of variance

to be explained by the other components. For the beam axis, PC1 accounted for approximately 90% of the variance. Moreover, for the latter case, the average similarity of PC1 across different

participants was high, _S_ = 0.99 ± 0.01. This indicates that the component accounting for the majority of the variance was also relatively invariant across participants. To test whether

these results changed across practice, the data were again split into 2 blocks (first 10 and second 10 of the successful trials) and PCA was applied separately to each block. There were no

noteworthy differences between the identified components, suggesting that there were no performance improvements during the experiment. When the AM was computed with respect to the head axis

_S_ was 0.93 ± 0.11 between block 1 and block 2. When the AM was computed with respect to the COM, _S_ was 0.94 ± 0.13, and when the center of the beam was taken as reference axis _S_ was

0.99 ± 0.02. The amount of variance accounted for by the first 5 PCs was always higher than 95%. As with the kinematic results, we also quantified the reproducibility of the coordination

structure between participants with a cross-validation procedure (see Methods). Using the components of a single participant, we predicted the data from other participants. With all pairwise

comparisons conducted for each of the 3 axes, the reproducibility measure was substantially lower for the whole-body COM reference axis, VAF = 86.67 ± 9.77%, and for the head axis, VAF = 

75.44 ± 23.80%, than for the beam axis, VAF = 98.93 ± 0.92%. These results show that the differences between individuals were much attenuated and again confirmed the robustness of the AM

patterns with respect to the beam axis. One might argue that the single dominant contribution to the AM from the trunk is a trivial consequence of the fact that the trunk is the body segment

with the largest mass. This might obscure the structure of the more complex coordination patterns of the arms and the legs. To evaluate this objection, we applied PCA to a reduced data set

that included all AM contributions, except the one of the trunk segment. The results of this analysis are summarized in Figure 5. Figure 5a shows that even in this case 5 components

explained about 95% of the variance, separately for each axis. The amount of variance that could be accounted for using one single component was however notably smaller in Figure 5a than in

Figure 4a. For instance, 3 components, instead of one, were needed to account for 90% of VAF when the AM was computed the beam axis. Figure 4b depicts the first 5 principal components for

the 3 axes. As above, the sets of principal components of different participants were paired and grouped according to their similarity before their averages were computed. There were still

considerable differences between the 3 axes with respect to the structure of the identified components. Remarkably, the components relative to the beam axis retained their particularly

intuitive structure, similar to what was seen in Figure 4b. Now, however, PC1 was associated mainly with the head segment, whereas the other 4 components were associated with the 2 arms and

the 2 legs (Fig. 5b). Figure 5c illustrates how the variance was distributed across the different components. Similar to the full set of components in Figure 4c, when the AM was computed

with respect to the head axis, all components accounted for a comparable amount of data variation. For the COM and the beam axis, however, the amount of VAF associated with PC1 was much

lower than in Figure 4c and is comparable to the VAF associated with the other components. These results therefore support the conclusion that, even when the trunk was excluded from the

analysis, the AM organization associated with the beam axis was still revealed simpler coordination patterns. This suggests that the simple AM organization was not the trivial consequence of

the large mass of the trunk. In order to assess the contributions of specific body segments to the coordination of the AM we quantified the percentage of VAF by head, trunk, arms and legs

separately. The results are summarized in Table 2. Clearly, the legs alone accounted for the largest amount of variance when the AM was computed with respect to the head axis. This

percentage was substantially lower for the whole-body COM and the beam axis. In contrast, the trunk segment accounted for the largest percentage of the VAF when the AM was computed with

respect to the beam axis. Its contribution was smaller for the other 2 reference axes. The arms provided similar contributions when the AM was computed with respect to the head or the COM

axes, but their contribution was smaller when computed with respect to the beam axis. Besides the 20 successful trials that each participant accomplished during the experiments, we also

analyzed the sets of unsuccessful trials during which participants lost their balance before arriving at the end of the beam. More specifically, for each participant we applied the same PCA

with VARIMAX rotation to the segmental orientations and computed the AM contributions with respect to the beam axis. The analysis was restricted to the last 3 seconds prior to termination,

defined as the moment when one foot touched the ground. The principal components of the unsuccessful trials were then compared to those of the successful ones. Using the same

cross-validation procedure as above, we quantified to which extent the principal components in the successful trials could account for data variation in the unsuccessful trials. For the

segmental kinematics, 8 principal components were needed to account for 95% of the variance in the unsuccessful trials, VAF = 93.93 ± 2.46%. The similarity between the components in

successful and unsuccessful trials was relatively high, but was highly variable, _S_ = 0.88 ± 0.21. Moreover, the principal components of the successful trials could not account for much of

the variance in the unsuccessful trials, VAF = 63.22 ± 15.32%. These results suggested that when participants started to lose balance they recruited different kinematic strategies than the

ones in the successful trials. When testing the segmental AM contributions, we found that in the unsuccessful trials 5 principal components could always account for at least 99% of the

variance and that these components were very similar to those associated with the successful trials, _S_ = 0.95 ± 0.11. Moreover, the cross-validation procedure revealed that the principal

components in the successful trials reconstructed the AM variation in the unsuccessful trials with high approximation, VAF = 98.75 ± 0.71%. These results therefore suggest that while the

kinematic coordination deviated from the steady-state pattern, the loss of balance was not preceded by a recruitment of altered AM components. The low-dimensional AM organization that

characterized both successful and unsuccessful trials suggests that the AM pattern arose from a linear combination of invariant AM patterns (the PCs). To further examine this conjecture, the

linear weights associated with the PCs were analyzed. The specific hypothesis was that loss of balance was brought about by a different combination of the principal components in comparison

to the successful trials. To investigate this hypothesis, the coefficient of the first AM principal component (PC1), explaining at least 90% of the variance, was related to a task variable

that characterized the degree of balance. The task variable that quantified ML balance, the ML velocity of the center-of-mass (VCOM) was chosen (Fig. 1b). Differences in the coefficients of

successful and unsuccessful trials should reflect different recruitment processes of the component. More specifically, we hypothesized that the RMS value of the time series of the linear

weight of PC1, computed within each single trial, should be predicted by the RMS of the time series of the VCOM, VCOMRMS, split by the type of trial (successful/unsuccessful) and their

interaction. A multiple regression revealed that such a linear model predicted a significant amount of the variance associated with the weight, F3,454 = 118.03, p < 0.002, R2 = 0.44,

R2adju = 0.43. Further, the type of trials did not significantly predict the coefficient, β = −0.112, t457 = −0.589, p > 0.05. In contrast, both VCOMRMS (β = 56.66, t457 = 8.06, p < 

0.001) and the interaction between trial type and VCOMRMS (β = −22.51, t457 = −6.30, p < 0.001) were significant predictors. The β values indicate the slopes associated with the

corresponding predictor in the regression equation. Taken together, the regression results showed that the weight of PC1 was approximately 2 times larger in the successful trials than in the

unsuccessful ones (see Fig. 6). This implies a weaker recruitment of this component in the instants prior to balance loss compared to the recruitment of the same component during the

successful trials. DISCUSSION The overall goal of this study was to investigate possible control strategies underlying the observed coordination during a challenging balancing task, walking

on a narrow beam. We found highly variable and complex kinematic patterns with large-amplitude movements of the trunk, arms and legs. This high variability in the kinematic patterns was

reflected in the high dimensionality of the relative orientations of the segments as quantified by a PCA. In addition, there appeared to be little or no consistency of patterns across the

different individuals, indicating a lack of invariance underlying the organization of the movements. Contrasting with this result, the analysis of the AM revealed a much simpler pattern.

Applying PCA to the AM structure of the different body segments, we were able to find a low-dimensional and coherent structure. This was especially the case when the AM was computed with

respect to an axis aligned with the beam. In contrast, when the AM was computed using the axes through the whole-body COM or the head, the revealed structures required more components to

approximate the data. Beam walking has been investigated in multiple previous studies2,3,4,6. However, in all these experiments, participants walked on the beam with their arms folded in

front of the body. The implicit or explicit reason was to isolate the locomotor task from disturbances arising from the complex and irregular arm movements. Simplifying the analysis of the

balancing components by excluding the influence of the arms can be advantageous when pursuing clinical goals6. However, it remains an open question how humans might control their entire body

including their arms to regulate balance. To answer this question, we opted to not impose constraints on the arm movements and allowed maximal freedom on the choice of motor strategies to

maintain balance. Indeed, participants moved their arms extensively (as visible by the loadings in PC1 to PC7 in Fig. 2), suggesting that the arms likely played a role in the control of

balance. This conclusion was also corroborated by the finding that 2 out of the 5 AM components were related to the arms. This underscores that to understand the control of locomotor balance

under relatively unstable conditions, it is necessary to examine arm movements. How can these results shed light on the control of balance? Our results might be interpreted with a

two-layered control framework21,22: an “execution” level and a “task” level. Rotating the body segments to control the whole-body AM about the beam axis to minimize the risk of falling may

reflect a control strategy that is concerned with lower-level variables, such as segmental AM contributions. This view is supported by the simple AM structure: the trunk, as a segment with

comparably high mass (about 43% of the total body weight23) and located relatively far away from the axis dominates the decomposition of the AM. The 2 legs and the 2 arms, which have much

smaller mass, are components that can be used for finer control or as measures of “last resort” to avoid loss of balance. This interpretation is supported by the fact that the the RMS values

of PC weights associated with the upper- and lower-limb components increased during the unsuccessful trials before participants lost balance and stepped off the beam (see supplementary Fig.

 S1). Note that the analysis that eliminated the trunk component ruled out that all structure was generated by the trunk component. At the task level the human body might be approximated by

an inverted pendulum that rotates about the axis that is defined by the contact of the feet with the beam24,25. Therefore, the corrections at the execution level might aim to ensure the

dynamic stability of the inverted pendulum. This raises the question how the body is controlled to assemble and regulate this inverted pendulum? Note that an inverted pendulum is by

definition unstable. Therefore, there has to be at least one additional degree of freedom to afford stability: either a joint at the hip to form a double-pendulum, or a joint at the tip of

the pendulum connected like a T-bar. Interestingly, these 2-DOF linkages map into well-known strategies when balancing: a two-DOF system may be achieved by moving around the hip joint, the

so-called hip strategy, well known in postural control9. The “T-bar model” is realized when the 2 arms are extended horizontally or even enhanced by rope walkers who hold a long horizontal

bar, evidently to help them maintain stability. The observation that the left and right arms are indeed the second and third PC is consistent with this T-bar model. The hypothesis that at

the task level the whole-body system may be approximated as an inverted pendulum does not contradict the fact that, at the execution level, a complex motor strategy may be applied. The

approach to approximate and simplify the whole body at the task level has revealed to also be useful in the control of robotic systems26,27. While balance of an inverted pendulum can be

achieved by applying, for example, zero-moment-point control, more refined control requires more accurate models28,29,30. Analysis of the unsuccessful trials provided interesting insights

into the strategies that participants recruited in the last 3 seconds before losing balance. Regardless of the chosen axis used for the AM computation, the AM components recruited in this

interval were similar to the ones recruited in the successful trials. On the one hand, this suggests that losing balance cannot be attributed to the recruitment of a “wrong” set of

components. Instead, the analysis suggests that the “right” components may be not be recruited properly, i.e. with the wrong linear weights, to assure balance recovery. The linear regression

analysis seemed to support this hypothesis. In the unsuccessful trials, the activation of the most important component (PC1) was much lower than its activation during the successful trials,

given a specific amount of dynamic instability VCOMRMS. This can be interpreted as a decrease of control effort and one possible cause of the loss of balance. However, the experimental

procedures were designed for the successful trials and more work is needed to develop more suitable procedures to reveal how the AM components are recruited and whether a deficient

recruitment process can lead to loss of balance. Angular momentum during walking has been investigated as a possible diagnostic measure for individuals with movement deficits caused, for

instance, by a stroke31,32,33,34,35,36,37. Analysis of gait stability in terms of the structure of angular momentum around different axes may inform clinicians about individual deficits and

may point to novel rehabilitation protocols for patients with balance problems. Our results showed that the RMS value of the medio-lateral velocity of the COM and the scalar coefficient of

the first principal component can discriminate between successful and unsuccessful trials. Hence, the coefficients of the AM principal components may be informative for the assessment of

balance problems and motor recovery during rehabilitation. Similarly, the number and amount of variance of principal components might help discriminate between different pathological changes

and help in the design and assessment of individual rehabilitation protocols. While the more standard clinical measures of functional impairment, such as the velocity of the COM, are easier

to obtain, the typical clinical measures tend to be global descriptors. We conjecture that the parameters of the low-dimensional organization might be more sensitive to specific

pathological factors and ultimately more precise and specific as diagnostic tools. Our study showed that computing the AM with respect to axes different from the typically used axis of the

whole-body COM provide novel and interpretable results. An interesting question therefore arises whether these methods and results generalize to other walking conditions. On the one hand,

normal walking on flat ground is comparatively stable in the ML plane and analysis of the AM with different axes may not provide new information as the limb rotations in the ML plane are

comparatively small. For example, the computation of the AM along the sagittal plane might provide useful insights as walking implies a rotational motion about the ankle of the standing leg

in the sagittal plane. Similar considerations apply to walking on stairs or slopes15,16. On the other hand, analysis with respect to the reference axis of the head may prove insightful for

many other balance-challenging walking conditions as head stabilization is an important reference for control during several locomotion tasks20. In conclusion, our results may serve as

stimulus to consider alternative axes when analyzing whole-body control in locomotory tasks. METHODS PARTICIPANTS Sixteen healthy participants completed the experiment (11 males, 5 females,

ages 27 ± 4 years, mass 70 ± 11 kg, height 1.76 ± 0.09 m). All participants were in good health and had no previous history of neuromuscular disease. The experiment conformed to the

Declaration of Helsinki and written informed consent was obtained from all participants according to the protocol approved by the ethical committee at the Medical Department of the

Eberhard-Karls-Universität of Tübingen, Germany. Participants appearing in the figures or in the supplementary videos provided informed consent for publication of identifying

information/images in an online open-access publication. KINEMATIC MEASUREMENTS Kinematic data were collected with a Vicon motion capture system with 10 infrared cameras (Oxford, UK), which

recorded the 3D positions of spherical reflective markers (2.5 cm diameter). The markers were attached with double-sided adhesive tape to tight clothing worn by the participants (Fig. 7a).

Marker placement followed the Vicon’s PlugInGait marker set. The sampling rate was set at 100 Hz; spatial error was below 1.5 mm. To create a challenging condition for balance control

participants walked on a very narrow beam (3.4 cm wide, 3.4 cm high, 4.75 m long). The beam was fixed to the ground with strong double-sided adhesive. In the Vicon frame of reference the

axis parallel to the beam was defined as the _x_-axis (Fig. 7b); the axis perpendicular to the beam was defined as _y_-axis, with positive pointing leftward with respect to the direction of

motion; the third axis parallel to the gravity direction was defined as _z_-axis, pointing upward. EXPERIMENTAL PROCEDURE Each participant was asked to walk barefoot from one end of the beam

to the other. Starting from a standing position with the left foot on the beam and the right foot on the ground, he/she started walking after the experimenter gave a go-signal and started

the movement recording. Importantly, participants were allowed to freely move their arms to maintain balance and there were no time constraints. After reaching the end of beam, the

participant stepped off the beam with both feet on either side of the beam and stood still until the movement recording was stopped. A typical successful trial lasted between 4.51 and 23.28 

seconds. The participant then returned to the starting position. If the participant lost balance and stepped off the beam before reaching the end, the experimenter stopped the recording and

the participant returned back to the starting position. A typical unsuccessful trial lasted between 0.96 and 18.89 seconds. Each participant performed trials until 20 successful trials were

completed. After each trial, participants were allowed to take a short rest if needed. Participants needed on average 34 ± 16 trials to achieve 20 successful trials. While there were 14

unsuccessful trials per participant, this number varied widely between 0 and 52 trials across individuals. DATA ANALYSIS Commercial Vicon software was used to reconstruct and label the

markers, to interpolate between short missing segments of the trajectories, and to compute the center-of-mass (COM) of the whole body. Kinematic analysis was performed off-line using Matlab

v.R2015a (The Mathworks, Natick, MA). Before analysis, kinematic data were low-pass-filtered using a Butterworth filter with a cut-off frequency of 20 Hz. To exclude transient behaviors,

only the time windows between 15% and 85% of the duration of each successful trial were considered for analysis. For each unsuccessful trial only the last 3 seconds before the participant

stepped off the beam were considered. Unsuccessful trials shorter than 2.5 seconds were excluded from the analysis. After this exclusion, there were 151 unsuccessful trials in total, on

average 9 ± 12 trials per participant, varying between 0 and 39 trials across individuals. As this study was mainly interested in understanding the organization of the kinematics and the AM

for balance control in the medio-lateral (ML) plane, the kinematic analysis was confined to this ML plane. RELATIVE ORIENTATIONS OF THE BODY SEGMENTS The human body was modeled as a

kinematic chain composed of 14 rigid segments: head, trunk, left and right upper arms, forearms, hands, thighs, shanks and feet. The spatial coordinates of the extrema of each segment (i.e.,

the ends of each link) were derived from the motion capture data. For the head, the first coordinate was obtained computing the average position between the centers of rotation of the left

and right shoulder, the second coordinate was defined at the average position of the 4 markers attached to the head. These coordinates were used to determine the axis parallel to the beam

but through the head. For each hand, one extremum coincided with the wrist joint, and the other one with the marker applied to the base of the index finger on the back of the hand. For each

foot, the first extremum coincided with the ankle joint of rotation, the second extremum with the marker applied on the top of the big toe. The 3D spatial coordinates of the joints of

rotation were projected onto the ML plane by setting the coordinates of the joints of rotation along the beam direction (_x_-axis) to zero. For each segment, its relative orientation was

computed as the angle between that segment and its proximal and adjacent segment. The orientation of the trunk segment was computed with respect to the _z_-axis. ANGULAR MOMENTUM The

contribution L _i_ (R _p_ ) of each segment to the whole-body angular momentum (AM) with respect to an axis of rotation passing through the point _P_ was computed as follows:

$${{\bf{L}}}_{i}({{\bf{r}}}_{P})=({{\bf{r}}}_{COM,i}-{{\bf{r}}}_{P})\times {m}_{i}({{\bf{v}}}_{COM,i})+{{\bf{I}}}_{i}{{\boldsymbol{\omega }}}_{i}$$ (1) where R_COM_,_i_ indicates the

position vector of the center-of-mass of the _i_-th segment, V_COM_,_i_ its corresponding velocity, I _i_ its inertial tensor, and ω _i_ its corresponding 3D angular velocity. R _p_

indicates the position vector of the point _P_. For each segment, the position of the corresponding center of mass and the inertial tensors I _i_ were computed using average human

anthropometric data and the kinematic measures derived from the motion capture data38,39,23. As the analysis focused on the movements in the ML plane, only the AM component parallel to the

_x_-direction was considered. This is the component of the vector L that causes rotations of the body segments in the ML plane. For each participant, the AM was computed about 3 axes passing

through 3 different points in the ML plane (Fig. 7b): (1) the average position of the head computed across all trials, (2) the position of the whole-body COM over time, and (3) the center

of the beam. The center of the beam and the average position of the head of each participant were fixed points in the ML plane. In contrast, the position of the whole-body COM changed over

time. However, it is well known that, for the COM, the derivative of the AM computed with respect to the _x_-axis passing though the COM is always equal to the external moments applied to

the body. The Euler’s law10 was therefore always valid independently of the chosen axis. The total AM was computed by summing the contributions of all body segments:

$${\bf{L}}({{\bf{r}}}_{P})={\sum }_{i=1}^{14}{{\bf{L}}}_{i}({{\bf{r}}}_{P}),$$ (2) INDEX OF STABILITY The velocity of the whole-body center-of-mass along the ML direction, VCOM, showed

marked fluctuations in time, coincident with variations in segmental kinematics (see Fig. 1 for illustration). To characterize this ML velocity, the root mean square error (RMS) was

calculated over the specified duration of each successful and unsuccessful trial VCOMRMS. ANALYSIS OF DIMENSIONALITY Principal component analysis40 (PCA) is an unsupervised learning method

that allows to decompose an input matrix X into the linear combination of a finite set of orthonormal basis vectors, referred to as principal components. These basis vectors are weighted by

a set of scalar coefficients. In order to analyze the spatio-temporal coordination of the relative orientations of the body segments, PCA was applied to the covariance matrix of the

segmental orientations. To analyze the dimensionality of the segmental AM contributions, PCA was applied to the covariance matrix of the AM components parallel to the walking direction, i.e.

the direction causing the rotation of the body segments in the frontal plane. In order to reduce the variability across study participants, the AM contributions were represented in

dimensionless form prior to PCA. For this purpose, they were normalized with respect to the product between the participant’s body mass (kg), walking speed (m/s) and body height (m). The

covariance matrix was used instead of the correlation matrix to avoid any amplitude normalization of the signals from different orientations or body segments. Subsequently, only the minimum

number of components was retained that was sufficient to account for at least 95% of the total variance (VAF)41. A VARIMAX rotation was applied to the retained components to simplify the

interpretation of the factors42. The direct effect of the VARIMAX rotation was a sparsification of the components, making the elements of each component very small or zero. The fewer

elements of the components are different from zero, the easier it is to provide a functional interpretation of the components. To quantify the level of sparseness for each rotated factor,

Hoyer’s index was used43. More specifically, sparsity was defined as follows: $${\rm{Sparsity}}=(\sqrt{N}-{\ell }_{1}/{\ell }_{2})\cdot {(\sqrt{N}-1)}^{-1},$$ (3) where _N_ indicates the

number of elements in each component (here _N = _14 for both segmental orientations and AM contributions) and \(\ell \)1 and \(\ell \)2 indicate the 1-norm and the 2-norm, respectively. This

measure varies between 0 and 1, where zero means that the factor is not sparse, and 1 signifies the maximum level of sparsity, where only one element of the factor is different from zero.

SIMILARITY BETWEEN COMPONENTS In order to assess similarity between different principal components associated with different axes, different participants, or the 2 types of trials

(successful versus unsuccessful), a similarity measure _S_ was computed for all possible pairings. To obtain the similarity _S_, the corresponding scalar product was computed after the

components were normalized with respect to their norms. Thus, given 2 principal components U and V, their similarity was defined as follows: $${S}=\frac{{\bf{u}}\cdot {\bf{v}}}{\Vert

{\bf{u}}\Vert \Vert {\bf{v}}\Vert }$$ (4) where \(\Vert \cdot \Vert \) indicates the Euclidian norm. The index _S_ represents the cosine of the angles between the vectors identified by the 2

components. When the index is equal to 1, the components are proportional to each other, while _S_ = 0 implies that they are orthogonal. The index _S_ is equivalent to the uncentered

Pearson correlation coefficient. The principal components of this first best-matching pair were then removed from the corresponding sets and the procedure was repeated for the second-best

matching pair, and so forth. This procedure was iterated until all components had been matched. The computation of the similarity _S_ between 2 sets of components provided a quantitative

assessment of the extent to which the patterns of covariation of the segmental orientations or segmental AM contributions relative to 2 axes, 2 participants, or successful or unsuccessful

trials differed from each other. CROSS-VALIDATION A cross-validation procedure was performed to assess the extent to which the organizations of the relative orientations of the body segments

and of the AM identified by PCA were invariant across participants or successful or unsuccessful trials. Each set of principal components identified in one participant or in one type of

trial was used to reconstruct the data from the other participants by least-square approximation. The goodness of reconstruction was quantified in terms of variance accounted for. The

goodness-of-fit measures were averaged across all pairings between participants to obtain a single reproducibility score. We also computed the extent to which head, trunk, arms and legs

contributed separately to the total AM. Their contributions were quantified in terms of percentage of variance accounted for. STATISTICAL ANALYSIS Mean and standard deviation were used to

summarize the data. The similarity between 2 time series was quantified by computing the corresponding centered Pearson’s correlation coefficient _R_. The amplitudes of temporal signals were

characterized by computing the corresponding root mean square values RMS. A Welch t-test was applied to compare RMS values of medio-lateral velocity across participants and trials, i.e.

with unequal and different sample sizes. A multiple regression analysis was conducted to test whether COM-stability in the ML plane (quantified by VCOMRMS), the type of trial

(successful/unsuccessful) and their interaction predicted the RMS value of the scaling coefficient associated with one principal component (the one associated with the trunk segment and

obtained from the AM computed with respect to the trunk). DATA AVAILABILITY The data that support the findings of this study are available from the authors of the article. Restrictions apply

to the general availability of these data, which were used under license for the current study, and so are not publicly available. However, data are available from the authors upon

reasonable request. CHANGE HISTORY * _ 18 APRIL 2018 A correction to this article has been published and is linked from the HTML and PDF versions of this paper. The error has been fixed in

the paper. _ REFERENCES * Bauby, C. E. & Kuo, A. D. Active control of lateral balance in human walking. _Journal of Biomechanics_ 33(11), 1433–1440 (2000). Article  CAS  PubMed  Google

Scholar  * Speers, R. A., Ashton-Miller, J. A., Schultz, A. B. & Alexander, N. B. Age differences in abilities to perform tandem stand and walk tasks of graded difficulty. _Gait and

Posture_ 7, 207–213 (1998). Article  CAS  PubMed  Google Scholar  * Domingo, A. & Ferris, D. P. Effects of physical guidance on short-term learning of walking on a narrow beam. _Gait and

Posture_ 30(4), 464–468 (2009). Article  PubMed  PubMed Central  Google Scholar  * Sipp, A. R., Gwin, J. T., Makeig, S. & Ferris, D. P. Loss of balance during balance beam walking

elicits a multifocal theta band electrocortical response. _Journal of Neurophysiology_ 110(9), 2050–2060 (2013). Article  PubMed  PubMed Central  Google Scholar  * Sawers, A., Allen, J. L.

& Ting, L. H. Long-term training modifies the modular structure and organization of walking balance control. _Journal of Neurophysiology_ 114(6), 3359–3373 (2015). Article  CAS  PubMed 

PubMed Central  Google Scholar  * Sawers, A. & Ting, L. H. Beam walking can detect differences in walking balance proficiency across a range of sensorimotor abilities. _Gait and Posture_

41(2), 619–623 (2015). Article  PubMed  Google Scholar  * Hof, A. L. An explicit expression for the moment in multibody systems. _Journal of Biomechanics_ 25, 1209–1211 (1992). Article 

MathSciNet  CAS  PubMed  Google Scholar  * Hof, A. L. The equations of motion for a standing human reveal three mechanisms for balance. _Journal of Biomechanics_ 40, 451–457 (2007). Article

  PubMed  Google Scholar  * Runge, C. F., Shupert, C. L., Horak, F. B. & Zajac, F. E. Ankle and hip postural strategies defined by joint torques. _Gait and Posture_ 10, 161–170 (1999).

Article  CAS  PubMed  Google Scholar  * Meriam, J. L. & Kraige, L. G. _Engineering Mechanics: Dynamics_ (John Wiley & Sons, 2012). * Herr, H. & Popovic, M. Angular momentum in

human walking. _The Journal of Experimental Biology_ 211(Pt 4), 467–481 (2008). Article  PubMed  Google Scholar  * Martelli, D., Monaco, V., Bassi Luciani, L. & Micera, S. Angular

momentum during unexpected multidirectional perturbations delivered while walking. _IEEE Transactions on Biomedical Engineering_ 60(7), 1785–1795 (2013). Article  PubMed  Google Scholar  *

Robert, T., Bennett, B. C., Russell, S. D., Zirker, C. A. & Abel, M. F. Angular momentum synergies during walking. _Experimental Brain Research_ 197(2), 185–197 (2009). Article  PubMed 

Google Scholar  * Silverman, A. K., Neptune, R. R., Sinitski, E. H. & Wilken, J. M. Whole-body angular momentum during stair ascent and descent. _Gait and Posture_ 39(4), 1109–1114

(2014). Article  PubMed  Google Scholar  * Silverman, A. K., Wilken, J. M., Sinitski, E. H. & Neptune, R. R. Whole-body angular momentum in incline and decline walking. _Journal of

Biomechanics_ 45(6), 965–971 (2012). Article  PubMed  Google Scholar  * Kajita, S. _et al_. Resolved momentum control: Humanoid motion planning based on the linear and angular momentum.

_Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems_, Las Vegas, NV, pp. 1644–1650 (2003). * Goswami, A. & Kallem, V. Rate of change of angular

momentum and balance maintenance of biped robots. _Proceedings of the IEEE International Conference on Robotics and Automation_, New Orleans, LA, USA, pp. 3785-3790 (2004). * Popovic, M.,

Hofmann, A. & Herr, H. Zero spin angular momentum control: definition and applicability. _Proceedings of the IEEE RAS/RSJ International Conference on Humanoid Robots_, Los Angeles, CA

(2004). * Macchietto, A., Zordan, V. & Shelton, C. R. Momentum control for balance. _ACM Transactions on Graphics (TOG)_ 28, 80 (2009). Article  Google Scholar  * Pozzo, T., Berthoz, A.,

Lefort, L. & Vitte, E. Head stabilization during various locomotor tasks in humans. _Experimental Brain Research_ 85, 208–217 (1991). Article  CAS  PubMed  Google Scholar  * Lockhart,

D. B. & Ting, L. H. Optimal sensorimotor transformations for balance. _Nature Neuroscience_ 10, 1329–1336 (2007). Article  CAS  PubMed  Google Scholar  * Tresch, M. C. A balanced view of

motor control. _Nature Neuroscience_ 10, 1227–1228 (2007). Article  CAS  PubMed  Google Scholar  * De Leva, P. Adjustments to Zatsiorsky-Seluyanov’s segment inertia parameters. _Journal of

Biomechanics_ 29, 1223–1230 (1996). Article  PubMed  Google Scholar  * Gage, W. H., Winter, D. A., Frank, J. S. & Adkin, A. L. Kinematic and kinetic validity of the inverted pendulum

model in quiet standing. _Gait and Posture_ 19, 124–132 (2004). Article  PubMed  Google Scholar  * Morasso, P. G., Baratto, L., Capra, R. & Spada, G. Internal models in the control of

posture. _Neural networks: the Official Journal of the International Neural Network Society_ 12(7–8), 1173–1180 (1999). Article  Google Scholar  * Kajita, S. _et al_. Biped walking pattern

generator allowing auxiliary zmp control, presented at Intelligent Robots and Systems. _Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems_, 2993–2999

(2006). * Kajita, S. _et al_. Biped walking pattern generation by using preview control of zero-moment point. _Proceedings of IEEE International Conference on Robotics and Automation_, vol.

2, 1620–1626 (2003). * Mukovskiy, A. _et al_. Adaptive synthesis of dynamically feasible full-body movements for the humanoid robot HRP-2 by flexible combination of learned dynamic movement

primitives. _Robotics and Autonomous Systems_ 91, 270–283 (2017). Article  Google Scholar  * Naveau, M., Carpentier, J., Barthelemy, S., Stasse, O. & Souères, P. METAPOD—Template

META-PrOgramming applied to dynamics: CoP-CoM trajectories filtering. _Proceedings of the IEEE RAS/RSJ International Conference on Humanoid Robots_, Madrid, Spain (2014). * Naveau, M. _et

al_. A reactive walking pattern generator based on nonlinear model predictive control. _IEEE Robotics and Automation Letters_ 2, 10–17 (2017). Article  Google Scholar  * Nott, C. R.,

Neptune, R. R. & Kautz, S. A. Relationships between frontal-plane angular momentum and clinical balance measures during post-stroke hemiparetic walking. _Gait and Posture_ 39(1), 129–134

(2014). Article  CAS  PubMed  Google Scholar  * Bruijn, S. M., Meyns, P., Jonkers, I., Kaat, D. & Duysens, J. Control of angular momentum during walking in children with cerebral palsy.

_Research in Developmental Disabilities_ 32(6), 2860–2866 (2011). Article  PubMed  Google Scholar  * Silverman, A. K. & Neptune, R. R. Differences in whole-body angular momentum between

below-knee amputees and non-amputees across walking speeds. _Journal of Biomechanics_ 44(3), 379–385 (2011). Article  CAS  PubMed  Google Scholar  * Sheehan, R. C., Beltran, E. J.,

Dingwell, J. B. & Wilken, J. M. Mediolateral angular momentum changes in persons with amputation during perturbed walking. _Gait and Posture_ 41(3), 795–800 (2015). Article  PubMed 

PubMed Central  Google Scholar  * Russell, S., Bennett, B., Sheth, P. & Abel, M. The gait of children with and without cerebral palsy: work, energy, and angular momentum. _Journal of

Applied Biomechanics_ 27(2), 99–107 (2011). Article  PubMed  Google Scholar  * Pickle, N. T., Wilken, J. M., Aldridge, J. M., Neptune, R. R. & Silverman, A. K. Whole-body angular

momentum during stair walking using passive and powered lower-limb prostheses. _Journal of Biomechanics_ 47(13), 3380–3389 (2014). Article  PubMed  Google Scholar  * Pickle, N. T., Wilken,

J. M., Aldridge Whitehead, J. M. & Silverman, A. K. Whole-body angular momentum during sloped walking using passive and powered lower-limb prostheses. _Journal of Biomechanics_ 49(14),

3397–3406 (2016). Article  PubMed  PubMed Central  Google Scholar  * Winter, D. A. _Biomechanics and motor control of human movement_ (John Wiley and Sons, 2009). * Zatsiorsky, V. M.,

Seluyanov, V. N. & Chugunova, L. G. Methods of determining mass-inertial characteristics of human body segments. _Contemporary Problems of Biomechanics_ 272, 291 (1990). Google Scholar 

* Jolliffe, I. _Principal component analysis_ (Wiley Online Library, 2002). * Mardia, K. V., Kent, J. T. & Bibby, J. M. Discriminant Analysis. In: _Multivariate Analysis_, 300–332

(Academic Press, London, 1979). * Kaiser, H. F. The varimax criterion for analytic rotation in factor analysis. _Psychometrika_ 23, 187–200 (1958). Article  MATH  Google Scholar  * Hoyer, P.

O. Non-negative matrix factorization with sparseness constraints. _Journal of Machine Learning Research_ 5, 1457–1469 (2004). MathSciNet  MATH  Google Scholar  Download references

ACKNOWLEDGEMENTS The research received funding from the European Union Seventh Framework, Koroibot FP7-ICT-2013-10/611909; DFG GI 305/4-1, DFG GZ: KA 1258/15-1; FP7-PEOPLE-2011-ITN (Marie

Curie): ABC PITN-GA-011-290011, CogIMon H2020 ICT-23-2014/644727, HFSP RGP0036/2016. Enrico Chiovetto was supported by the Institutional 431 Strategy of the University of Tübingen (Deutsche

Forschungsgemeinschaft, ZUK 63). Dagmar Sternad was supported by the National Institutes of Health R01-HD087089, R01-HD081346, and the National Science Foundation NSF-NRI-1637854,

NSF-EAGER-1548514, and NSF-CRCNS-1723998. Dagmar Sternad and Meghan Huber were also supported by the Max Planck Institute for Intelligent Systems, Tübingen, Germany. We acknowledge also

support by the Deutsche Forschungsgemeinschaft and the Open Access Publishing Fund of University of Tübingen. We thank Prof. Stefan Schaal and Dr. Ludovic Righetti, Max Planck Institute for

Intelligent Systems, Autonomous Motion Department, for helpful discussions. We also thank Prof. Neville Hogan for useful comments on earlier versions of the manuscript. AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Section for Computational Sensomotorics, Department of Cognitive Neurology, Hertie Institute for Clinical Brain Research, Centre for Integrative Neuroscience,

University Clinic Tübingen, Tübingen, Germany Enrico Chiovetto & Martin A. Giese * Department of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, Massachusetts,

USA Meghan E. Huber * Departments of Biology, Electrical and Computer Engineering, Physics, and Physical Therapy, Movement Science and Rehabilitation, Northeastern University, Boston,

Massachusetts, USA Dagmar Sternad Authors * Enrico Chiovetto View author publications You can also search for this author inPubMed Google Scholar * Meghan E. Huber View author publications

You can also search for this author inPubMed Google Scholar * Dagmar Sternad View author publications You can also search for this author inPubMed Google Scholar * Martin A. Giese View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS All authors conceived and designed the experiments. E.C. and M.H. carried out the experiments.

E.C. analyzed the data and drafted the manuscript. All authors discussed the results and implications. E.C., D.S. and M.G. wrote the final version of the manuscript. CORRESPONDING AUTHOR

Correspondence to Enrico Chiovetto. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare that they have no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE: Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY FIGURE SUPPLEMENTARY VIDEOS1

SUPPLEMENTARY VIDEOS2 SUPPLEMENTARY VIDEOS3 SUPPLEMENTARY VIDEOS4 SUPPLEMENTARY VIDEOS5 SUPPLEMENTARY VIDEOS6 RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative

Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the

original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in

the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended

use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Chiovetto, E., Huber, M.E., Sternad, D. _et al._ Low-dimensional organization of

angular momentum during walking on a narrow beam. _Sci Rep_ 8, 95 (2018). https://doi.org/10.1038/s41598-017-18142-y Download citation * Received: 21 July 2017 * Accepted: 06 December 2017 *

Published: 08 January 2018 * DOI: https://doi.org/10.1038/s41598-017-18142-y SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative