Reader TTS

Download PDF Article Open access Published: 13 August 2018 Delay-Induced Multistability and Loop Formation in Neuronal Networks with Spike-Timing-Dependent Plasticity Mojtaba Madadi Asl1,

Alireza Valizadeh1,2 & Peter A. Tass3  Scientific Reports volume 8, Article number: 12068 (2018) Cite this article

2853 Accesses

12 Altmetric

Metrics details

Spike-timing-dependent plasticity (STDP) adjusts synaptic strengths according to the precise timing of pre- and postsynaptic spike pairs. Theoretical and computational studies have revealed

that STDP may contribute to the emergence of a variety of structural and dynamical states in plastic neuronal populations. In this manuscript, we show that by incorporating dendritic and

axonal propagation delays in recurrent networks of oscillatory neurons, the asymptotic connectivity displays multistability, where different structures emerge depending on the initial

distribution of the synaptic strengths. In particular, we show that the standard deviation of the initial distribution of synaptic weights, besides its mean, determines the main properties

of the emergent structural connectivity such as the mean final synaptic weight, the number of two-neuron loops and the symmetry of the final structure. We also show that the firing rates of

the neurons affect the evolution of the network, and a more symmetric configuration of the synapses emerges at higher firing rates. We justify the network results based on a two-neuron

framework and show how the results translate to large recurrent networks.

plasticity Article Open access 02 September 2022 Dendrites help mitigate the plasticity-stability dilemma Article Open access 21 April 2023 Multicoding in neural information transfer

suggested by mathematical analysis of the frequency-dependent synaptic plasticity in vivo Article Open access 18 August 2020 Introduction

Spike-timing-dependent plasticity (STDP)1,2,3,4,5 modifies synaptic strengths according to the relative timing of pre- and postsynaptic spike pairs. When the postsynaptic spike follows the

presynaptic spike, a potentiation of the corresponding synaptic strength is induced by the STDP mechanism, whereas the synaptic strength is depressed in the opposite case2. STDP is a local

learning rule, where the synaptic modification only depends on the joint pre-post activity of the corresponding synapse. However, STDP may significantly impact on the global dynamics of

neuronal networks, so that qualitatively different connectivity patterns can emerge under the influence of STDP6,7,8,9,10,11,12,13,14,15,16,17. It is commonly accepted that the temporally

asymmetric learning window of the classic pair-based STDP eliminates strong bidirectional loops between neuronal connections18,19,20,21,22,23. Although this interesting feature of STDP can

explain the emergence of feedforward networks4,19,24,25, it is in contradiction to the prevalence of recurrent connections in cortical circuits26,27,28,29,30.

However, it is possible to stabilize strong bidirectional connections by employing variations of STDP22 or by considering independent noise31 in the plastic neuronal networks. On the other

hand, as shown recently, by taking into account dendritic and axonal propagation delays, the conventional pair-based additive STDP may lead to the emergence of different connectivity

patterns including both unidirectional and bidirectional connections, or decoupled neurons32.

An asymmetric learning window of STDP profile can push the network dynamics toward a synchronized state with strongly up-regulated synaptic connections, or conversely, the network can evolve

into a desynchronized regime with down-regulated synaptic strengths33,34,35,36,37. It was shown that the initial mean synaptic coupling determines the finally evolving mean strength of the

synaptic connections. Strong initial coupling leads to synchronized dynamics that can be enhanced and preserved by STDP, while weak initial connections lead to desynchronized states, i.e.,

there is a multistability of synchronized and desynchronized states in the plastic neuronal networks33,34,38. Hence, STDP-driven neuronal populations can induce different multistable

attractor states characterized by specific coupling regimes33,34,38.

Dendritic and axonal propagation delays within and between brain areas may assume different values and need not be identical. Dendritic delays are typically smaller than axonal delays20.

However, dendritic delays may range from sub-millisecond to a few milliseconds39,40, e.g. Agmon-Snir and Segev39 demonstrated that the dendritic delay in octopus cells is about 0.5 ms.

Axonal propagation delays may range from 0.3 ms in thalamo-cortical connections41 and 1 ms in cortico-tectal connections42 to 20 ms in cortico-cortical connections43, and even more, up to 40

 ms in cortico-thalamic circuits42.

The presence of dendritic and axonal propagation delays can regulate the emergent structures of STDP-driven plastic neuronal populations20,32. Propagation delays affect the function of STDP

in two different ways. First, the total propagation delay τ = τd + τa, i.e., the sum of the dendritic τd and axonal τa propagation delays, determine the synchronization tendency of the

coupled neurons and the time difference of spiking of the neurons44,45,46,47,48,49,50. Second, since the effect of pre- and postsynaptic neurons arrive at the synapse after axonal and

dendritic delays, respectively, the difference of the two propagation delays ξ = τd − τa, changes the relative timing at the synapse. We recently showed32 that by incorporating propagation

delays in a plastic neuronal network model, bidirectional connections can be retained and potentiated despite the previously reported simulation results with conventional STDP in the absence

of delays33,34,38.

In this study, we focus on the multistability of the structural dynamics of the network with respect to the distribution of the initial synaptic weights in coupled networks with delays.

Multistability was previously reported with respect to the mean initial synaptic weight: The final mean synaptic strength mainly depends on the initial average weight34,38. Here we show that

within the present framework not only the mean, but also the standard deviation of the initial connections crucially determines the final mean strength of the synapses. Moreover, the

presence of bidirectional connections and the symmetry of the final structure is determined by the initial discrepancy of the synaptic weights. We show that the multistability of the network

can be explained in a modular way, by the presence of different attractors for a two-neuron motif in the two-dimensional space of the initial connection strengths. We also show that the

domain of attraction of each final structural state depends on the firing frequency of the neurons: At high firing rates the attraction domain for symmetric connections grows in expense of

shrinking that of the unidirectional connections. This leads to a more symmetric final structure when the neurons are firing at higher rates. Intriguingly, all of these nontrivial phenomena

are only seen when the propagation delays are incorporated in the formulation of the model: Without propagation delays, any initial preparation ends up with unidirectional connections

regardless of the firing rate of the neurons and the initial weights of the synapses.

We consider two neuronal oscillators described in a phase reduced model. In this approach, the evolution equation for the relative phase of the two neuronal oscillators can be written as

follows (for the derivation see Methods, Eq. (6)):

}}=|\frac{{g}_{12}-{g}_{21}}{{g}_{12}+{g}_{21}}|,$$ (1)

where χ = φ2 − φ1 is the phase lag, \({\rm{\Omega }}\,=\,2\pi {\rm{\Delta }}\nu \) that Δν = ν2 − ν1 is the frequency mismatch, and ψ = 2πντ is the rescaled delay with τ = τd + τa being the

sum of dendritic τd and axonal τa propagation delays. The values for dendritic and axonal propagation delays are chosen based on the experimental observations in cortical areas42,43. The

quantity Γ reflects the relative difference of the synaptic strengths in two opposite directions, where gij with i, j = 1, 2 (j ≠ i) is the synaptic strength of the synapse connecting

presynaptic neuron j to postsynaptic neuron i.

The synapses connecting the two neurons are subjected to classic pair-based STDP rule where the synaptic strengths gij = gij(t) are modified based on the delayed time lag between pre- and

postsynaptic activity at synaptic site, i.e., \({\rm{\Delta }}{t^{\prime} }_{ij}={\rm{\Delta }}{t}_{ij}+\xi \)32 where Δtij = ti − tj is the time lag in the absence of propagation delays and

ξ = τd − τa is the difference between dendritic and axonal propagation delays. The synaptic strengths are updated by an additive rule at each step gij → gij + Δgij, according to the

following learning function (see Methods):

}),$$ (2)

where A+(A−) and τ+(τ−) are the learning rate and the effective time window of synaptic potentiation (depression), respectively, and sgn(Δt) is the sign function. The synaptic strengths are

bounded in the range (gmin, gmax) = [0.05, 1] by the hard bound saturation constraint4,51: The synaptic strengths are set to gmin (gmax) once they cross the lower (upper) limit of their

allowed range. We consider a balanced STDP profile4,19 with equal potentiation and depression contribution, i.e. A+ = A− and τ+ = τ−, in order to extract the pure influence of propagation

delay and oscillation frequency on the synaptic dynamics. We assumed that the changes in synaptic strengths are slow in comparison to the fast timescale of the system, therefore, the neurons

remain phase-locked despite of eventual change in the synaptic strengths. Given the firing frequency ν and assuming that the frequency mismatch between the two oscillators is negligible,

i.e. \({\rm{\Omega }}\simeq 0\), the fast timescale equation of the two-neuron motif (Eq. (1)) exhibits a stable fixed point which is given by Eq. (9), \({\chi }^{\ast

}={\rm{t}}{\rm{a}}{{\rm{n}}}^{-1}({\rm{\Gamma }}\,{\rm{\tan }}\,\psi )\), and hence firing time difference of two neurons at the stable state will be Δt* = χ*/(2πν). These values could be

inserted in Eq. (3) to give the evolution of the synaptic connections32,52.

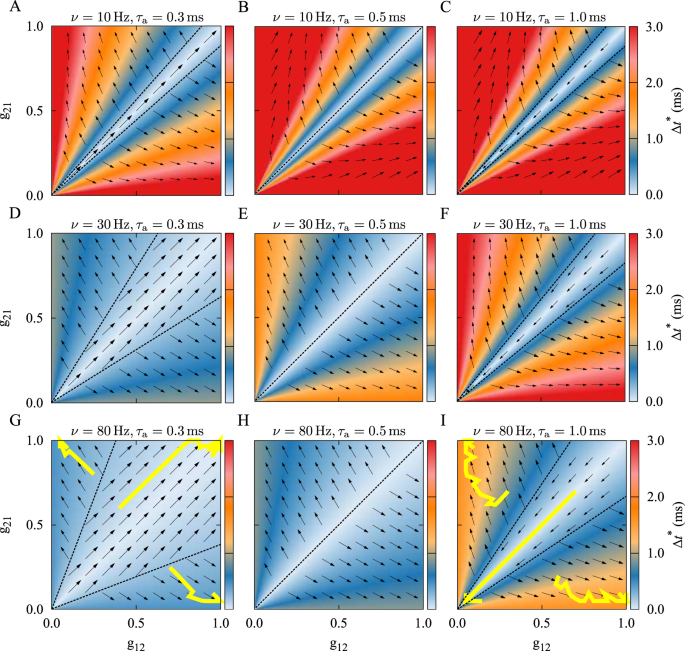
In Fig. 1 we show the synaptic dynamics (illustrated by the vector field) overlaid on the the representation of the instantaneous time lag of the spiking neurons (shown by colors), for the

different values of the initial synaptic strengths (g21(0), g12(0)). It can be seen that the basin of attraction for the three different final connectivity patterns (bidirectional,

unidirectional and decoupled) is determined by the firing frequency ν and the difference between dendritic and axonal delays ξ. The results shown in Fig. 1 denote the theoretical prediction

of different stable structural states that coexist for different combinations of delay and firing frequency. The colors indicate the stable fixed point of the time lag Δt* given by Eq. (9),

and the vector field shows the changes of the synaptic strengths from Eq. (3). Given the initial values of the synaptic strengths, the instantaneous color-coded fixed point of the time lag

determines the synaptic changes depicted by the vector field, and the subsequent values of the synaptic strengths. The corresponding trajectories of the time evolution of the synaptic

strengths resulted from numerical experiments with three different initial values are shown by yellow solid curves in Fig. 1G and I. The numerical solutions practically follow the vector

field directions predicted by the analytical results. The time course of the simulated synaptic strengths and the firing time lag are presented in Fig. 2.

Theoretical prediction of synaptic modification as a function of the initial synaptic strengths in the absence of a frequency mismatch. The colors show the stable fixed point of the time lag

Δt* = χ*/(2πν) of spiking of the neurons given by Eq. (9) and the vector field shows the direction of the change of the synaptic strengths from Eq. (3). The yellow solid curves denote the

simulated synaptic evolution for three different initial values. In each row, the firing frequency ν is constant, but it increases from top to bottom in each column. Based on the initial

synaptic coupling, different attractors may be achieved: Bidirectional/unidirectional (left column), unidirectional (middle column), and decoupled/unidirectional (right column) state. The

dendritic propagation delay is \({\tau }_{{\rm{d}}}=0.5\,\,{\rm{ms}}\) and the axonal delay is denoted above each panel. STDP parameters are A+ = A− = 0.005 and τ+ = τ− = 20 ms.

imageFigure 2

Time course of simulated synaptic strengths and spiking time lag. (A–C) Correspond to Fig. 1G with ν = 80 Hz and τa = 0.3 ms. (D–F) Correspond to Fig. 1I with ν = 80 Hz and τa = 1.0 ms. The

initially given two-dimensional synaptic strength vector is (g21(0), g12(0)) = (0.6, 0.4), (0.2, 0.7), (0.8, 0.2), (0.7, 0.7), (0.7, 0.3), (0.2, 0.6) for (A–F), respectively. The finally

achieved two-dimensional synaptic strength vector (g21, g12) is denoted in the figure.

Figure 1, left and right columns illustrate that according to different initial arrangements of the connections, the two-neuron motif will end up with one of the bistable coupling regimes:

Bidirectional/unidirectional coupling (Fig. 1, left column, dendritic delay is greater), or decoupled/unidirectional coupling (Fig. 1, right column, axonal delay is greater). The basin of

attraction of the symmetric coupling regimes (i.e. bidirectional or decoupled final configuration) grows with an increase of the firing frequency (Fig. 1, left and right columns, top to

bottom), making it more probable that in the high-frequency firing regime the neurons are either bidirectionally coupled (Fig. 1G) or remain decoupled (Fig. 1I).

We also examined the effect of a frequency mismatch Δν = ν2 − ν1, i.e. the difference between the frequencies of the two oscillators introduced in Eq. (1), on the evolution of the synapses.

Expectedly, the frequency mismatch shifts the border of the basins of attraction in a way that the neuron with the greater firing rate more likely wins the competition in generating a

stronger outgoing synapse and suppressing the reverse one (see Fig. 3), which is in accordance with previous studies21,53. However, for small frequency mismatches (e.g. Δν = 0.02 Hz in Fig. 

3A–C) bistability can still be present, and all three final configurations may be achieved depending on other parameters, i.e., the difference in propagation delays and firing

frequencies.

Theoretical prediction of synaptic modification based on the initial synaptic strengths in the presence of a frequency mismatch. In the presence of a frequency mismatch Δν, the instantaneous

fixed point of the time lag is numerically calculated by self-consistently solving Eq. (8) with the Newton-Raphson root-finding method. (A–C) Frequency mismatch Δν = 0.02 Hz with ν2 > ν1.

(D–F) Frequency mismatch Δν = 0.04 Hz with ν2 > ν1. In the presence of frequency mismatch the output synapse of the neuron with higher frequency is more likely to be potentiated, while the

reverse synapse is depressed.

The relation between dendritic and axonal delays is crucial to the emergence of bistability. When dendritic and axonal delays are equal, ξ = 0, which is equivalent to ignoring both in the

STDP implementation, no bistability emerges and the final connectivity pattern is unidirectional, regardless of the initial synaptic strengths (see Figs 1 and 3, middle columns). This is

consistent with the results of Babadi and Abbott23, obtained for a balanced STDP profile. Note, in our model the bistability and the possibility of the emergence of symmetric connectivity

patterns are observed for symmetric STDP just because the propagation delays are explicitly considered (also see Madadi Asl et al.32).

The dependence of the final stable coupling regimes on the initial values of the synaptic strengths can be explained based on Eq. (9), \({\rm{\Delta }}{t}^{\ast }={\tan }^{-1}({\rm{\Gamma

}}\,\tan \,\psi )\mathrm{/(2}\pi \nu )\), that gives the asymptotic time lag between pre- and postsynaptic spikes. Therefore, the instantaneous fixed point of the time lag (Eq. (9)) is

determined by the relative synaptic strength Γ, the firing frequency of the oscillation ν, and the total delay τ. In turn, the instantaneous value of Δt* determines the evolution of the

synaptic strengths according to Eq. (3). More specifically, the values of the synaptic strengths determine the relative synaptic strength Γ = |(g12 − g21)/(g12 + g21)| from Eq. (1), where

the interaction of the relative synaptic strength with the fixed point of the time lag \({\rm{\Delta }}{t}^{\ast }\) ultimately determines the final stable coupling regime. The right panels

of Fig. 4, show that the color-coded relative synaptic strength Γ is close to zero around the diagonal line (light color) and maximal at the corners (dark color). As shown in Fig. 4 (left

panels) the basin of attraction of the two-neuron motif changes when \({\rm{\Delta }}{t}^{\ast }\) (blue curve) crosses a certain value of Γ (denoted by arrow). The bistability is between

bidirectional (red) and unidirectional (orange) connections (Fig. 4A, left panel), or between decoupled (blue) and unidirectional (orange) states (Fig. 4B, left panel).

Dependence of the two-neuron results on the relative synaptic strength. (Left panels) The interplay between fixed point of the time lag \({\rm{\Delta }}{t}^{\ast }\) and relative synaptic

strength Γ determines the final stable connectivity pattern. Colors show the type of the final synaptic connectivity pattern: Bidirectional (red), unidirectional (orange), and decoupled

(blue). The blue curve denotes Δt* calculated from Eq. (9). (A) ν = 80 Hz and τa = 0.3 ms. (B) ν = 80 Hz and τa = 1.0 ms. The dendritic propagation delay is τd = 0.5 ms. (Right panels) The

color-coded relative synaptic strength Γ is shown based on the synaptic strengths from Eq. (1). The vector field is the same as in Fig. 1.

In the two-neuron motif the relative synaptic strength \(\Gamma \), given by Eq. (1), determines the final configuration of the connections (see Fig. 4). Small Γ favors more symmetric final

structure, and bidirectional connections can emerge if the axonal delays are small. Intriguingly, in large networks the initial distribution of the connection strengths is the key factor

determining the emergence of bidirectional connections: In an initially homogeneous network with narrow distribution of the synaptic strengths, bidirectional connections (i.e. two-neuron

loops) are more likely to survive in the network, while heterogeneity in the initial synaptic strengths drives the network to an asymmetric final structure with a small number of

bidirectional connections. In contrast, so far, the evolution of the network and the emergent structure was attributed only to the mean of the initial synaptic strengths33,34,38. In order to

study the generalization of our framework to the network level, we took a fixed value of the mean initial synaptic strength and varied the width of the distribution of the initial synaptic

strengths by changing the standard deviation σg of the distribution. We constructed an initially fully connected network of N = 200 excitatory neurons. Synaptic strengths are modified based

on the pair-based additive STDP rule given by Eq. (2). Based on the analysis for the case of a two-neuron motif, the dynamics of the network for a given relative delay (difference of axonal

and dendritic delays) and firing frequency can be predicted by the initial distribution of the synaptic strengths. Figure 5 shows the results for the recurrent excitatory network with

relative delay ξ = 0.2 ms, as in the case of short-range synaptic projections, in the high-frequency firing regime. The dendritic delay τd = 0.5 ms is greater than the axonal τa = 0.3 ms.

According to Fig. 1G, our analysis of the two-neuron motif predicts a multistability regarding the number of bidirectional and unidirectional connections in the emergent network. Figure 5A,

left panel shows the time evolution of the mean synaptic strength, and right panel illustrates the initial and final distribution of the synaptic strengths where the network architecture is

dominated by either bidirectional loops (blue distribution) or unidirectional connections (grey distribution). Figure 5B, left panel shows the synchronization degree of the neuronal

oscillators and right panel represents the number of two-neuron loops. Figure 5C shows the final coupling matrices for pre- and postsynaptic neurons. For smaller values of the standard

deviation (e.g. σg = 0.05, 0.08 in Fig. 5C), based on our two-neuron motif analysis, the network is driven to potentiate bidirectional connections. However, for greater values of the

standard deviation (e.g. σg = 0.10, 0.15 in Fig. 5C), in the emergent structure unidirectional connections have more chance to survive.

Simulation results for a recurrent excitatory neuronal network in the high-frequency regime with heterogeneous initial synaptic strengths and ξ > 0. (A) (Left panel) Time course of the mean

synaptic strength \(\bar{g}\)(t) for different standard deviations σg. (Right panel) Initial and final distribution of the synaptic strengths. (B) (Left panel) Time course of the order

parameter r(t). Note that the colors indicated in the legend belong to the same σg in A and B. (Right panel) Time course of the normalized number of closed loops of length 2 (see Methods),

representing the number of bidirectional connections in the network. (C) Final coupling matrices for σg = 0.05,0.08,0.10,0.15, respectively. Network and STDP parameters are N = 200, \(\nu

=80\,{\rm{H}}{\rm{z}}\), τd = 0.5 ms, τa = 0.3 ms, A+ = A− = 0.005, and τ+ = τ− = 20 ms.

For large axonal delays, as in the case of long-range synaptic projections, a similar bistability is observed between unidirectional connections and a disconnected network. Figure 6 shows

the results for ξ = −0.5 ms. The axonal delay τa = 1.0 ms is greater than the dendritic τd = 0.5 ms. Figure 6A, left panel shows the evolution of the mean synaptic strength in the network,

and right panel represents the initial and final distribution of the synaptic strengths where the network structure tends to be decoupled (blue distribution) or dominated by unidirectional

connections (grey distribution). Figure 6B, left panel shows the synchronization degree of the neuronal oscillators and right panel represents the number of two-neuron loops. Figure 6C shows

the final coupling matrices for pre- and postsynaptic neurons. In the case with small standard deviation of the synaptic strengths (e.g. σg = 0.05, 0.08 in Fig. 6C), most of the connections

tend to be depressed. In contrast, for wider distributions (e.g. \({\sigma }_{g}=\mathrm{0.10,}\,0.15\) in Fig. 6C), the synapses get unidirectionally potentiated. Note that the stability

of the disconnected network in our simulations relies on our choice of the lower hard bound of the synaptic strength, gmin. Assigning a finite value for gmin stabilizes the network structure

at a point where all connections attain the minimum value. Setting the minimum synaptic weight at zero, destabilizes the disconnected network, and one of the synapses builds up to achieve a

unidirectional link. Our choice seems reasonable based on the experimental results on STDP3,5. The emergence of a stable decoupled state in the phase-locked mode can, e.g., be of importance

for the development of stimulation methods for neurological disorders designed to induce long-lasting, sustained therapeutic effects by shifting a neuronal network from phase-locked

attractors to more favorable, decoupled attractors38,54,55.

Simulation results for a recurrent excitatory neuronal network in the high-frequency regime with heterogeneous initial synaptic strengths and ξ > 0. (A) (Left panel) Time course of the mean

synaptic strength \(\bar{g}\)(t) for different standard deviations σg. (Right panel) Initial and final distribution of the synaptic strengths. (B) (Left panel) Time course of the order

parameter r(t). (Right panel) Time course of the normalized number of closed loops of length 2, representing the number of bidirectional connections in the network. (C) Final coupling

matrices for σg = 0.05,0.08,0.10,0.15, respectively. Network and STDP parameters are N = 200, ν = 80 Hz, \({\tau }_{{\rm{d}}}=0.5\,\,{\rm{ms}}\), τa = 1.0 ms, A+ = A− = 0.005, and τ+ = τ− = 

20 ms.

By decreasing the firing frequency and increasing the disparity of the neuronal firing rate the symmetric (bidirectional or decoupled) connections are less likely to survive as revealed by

the two-neuron motif analysis (Figs 1 and 3). We extracted the probability (Pasym) of appearance of unidirectional connections in the two-neuron motif, by taking the ratio of the area in the

(g21, g12) space which leads to unidirectional connections to the total area of the same parameter space. Figure 7A shows that this probability is a decreasing function of frequency. To

investigate the impact of this result on the evolution of the network, we defined the network asymmetry index Cnet which quantifies the average asymmetry of the connections between pairs of

neurons (see Methods). Expectedly, the network asymmetry index shows a similar decreasing trend which indicates that the number of unidirectional connections in the network decreases with

increasing frequency (see Fig. 7A). As shown in Fig. 7B, by increasing the frequency of the oscillations, network asymmetry index decreases, which is consistent with a similar decrease in

Pasym in the two-neuron motif, indicating that at higher frequencies the probability of the appearance of symmetric connections (two-neuron loops or decoupled pairs) increases. Also, based

on the results of Fig. 3, a sufficiently pronounced inhomogeneity in the firing rate of the neurons can prevent the formation of strong bidirectional connections. Figures 8 and 9 show the

network results in the presence of heterogeneous firing frequencies. Left panels in Figs 8A and 9A represent the mean synaptic strength and right panels illustrate the distribution of the

firing frequencies and the final synaptic strengths based on the inhomogeneity in the distribution of the firing rates. Left panels in Figs 8B and 9B show the order parameter of the

oscillators, whereas right panels represent the number of two-neuron loops in the network which is suppressed by increasing the inhomogeneity in the distribution of the firing rates. Figures

 8C and 9C show the final coupling matrices for pre- and postsynaptic neurons. As shown in Figs 8 and 9, by increasing the standard deviation σν of the distribution of the firing rates, the

number of loops in the final structure decreases. This is also illustrated in Fig. 7C where the asymmetry index Cnet increases with increasing σν. The probability Pasym in the two-neuron

motif also follows the same ascending trend. Figure 7D shows that by increasing the inhomogeneity in the initial distribution of the synaptic strengths with standard deviation σg,

unidirectional connections with high values of the asymmetry index are more likely to emerge. This increasing trend was also generally predicted by the probability Pasym in the two-neuron

motif based on our theoretical framework.

Illustration of the accordance between two-neuron theoretical framework and network simulation results. (A–D) The probability Pasym as a measure of asymmetry in the two-neuron motif (solid)

and the asymmetry index \({C}_{{\rm{net}}}\) for the neuronal network (dotted curves) are calculated in the presence of different axonal propagation delays with τa = 0.3 ms (red) and τa = 

1.0 ms (blue curves). (A) The effect of the firing frequency on Pasym (Cnet) in the two-neuron motif (network simulation) with inhomogeneity in the initial distribution of the synaptic

strengths represented by σg. In the figure σg = 0.05. (B) Same as A, but in the presence of inhomogeneity in the firing frequencies indicated by Δν (\({\sigma }_{\nu }\)) in the two-neuron

motif (network simulation). In the figure Δν = σν = 0.01 Hz. (C) The effect of inhomogeneity in the frequencies Δν (σν) on Pasym (Cnet). In the figure ν = 80 Hz and σg = 0.05. (D) Same as C,

but for inhomogeneity in the initial distribution of the synaptic strengths σg. In the figure ν = 80 Hz and Δν = σν = 0.01 Hz. (a1–d1) Samples of final coupling matrix indexed by the number

of pre- (j) and postsynaptic (i) neurons correspond to a1–d1 markers in A–D, representing the value of the asymmetry index Cnet = 0.31,0.00,0.75,0.64,0.62,0.80 in the simulated network,

respectively.

Simulation results for a recurrent excitatory neuronal network in the high-frequency regime with heterogeneous firing frequencies and ξ > 0. (A) (Left panel) Time course of the mean synaptic

strength \(\bar{g}\)(t) for different standard deviations σν. (Right panel) Distribution of the firing frequencies and the final synaptic strengths. (B) (Left panel) Time course of the

order parameter \(r(t)\). (Right panel) Time course of the normalized number of closed loops of length 2, representing the number of bidirectional connections in the network. (C) Final

coupling matrices for σν = 0.01, 0.02, 0.03, 0.04 Hz, respectively. Network and STDP parameters are N = 200, \(\bar{\nu }\) = 80 Hz, τd = 0.5 ms, \({\tau }_{{\rm{a}}}=0.3\,\,{\rm{ms}}\), A+ 

= A− = 0.005, and τ+ = τ− = 20 ms.

Simulation results for a recurrent excitatory neuronal network in the high-frequency regime with heterogeneous firing frequencies and ξ > 0. (A) (Left panel) Time course of the mean synaptic

strength \(\bar{g}\)(t) for different standard deviations \({\sigma }_{\nu }\). (Right panel) Distribution of the firing frequencies and the final synaptic strengths. (B) (Left panel) Time

course of the order parameter r(t). (Right panel) Time course of the normalized number of closed loops of length 2, representing the number of bidirectional connections in the network. (C)

Final coupling matrices for σν = 0.01, 0.02, 0.03, 0.04 Hz, respectively. Network and STDP parameters are N = 200, \(\bar{\nu }\) = 80 Hz, τd = 0.5 ms, \({\tau

}_{{\rm{a}}}=1.0\,\,{\rm{ms}}\), A+ = A− = 0.005, and τ+ = τ− = 20 ms.

STDP is conventionally known as a mechanism which generically breaks the structural symmetry of neuronal networks and underlies the formation of feedforward networks4,19,24,25,56. This

result in recurrent networks contradicts the experimental observations in cortical circuits where bidirectional connections are frequent26,27,28,29,30. Bidirectional connections can be

retained through alternative versions of conventional STDP: Triplet-based STDP57 and STDP with a shifted profile23. Triplet-based STDP, which has been designed to conform the dependence of

the experimentally observed synaptic changes to the firing rates58, can promote bidirectional connections in the high-frequency regime57. Pair-based STDP with a rightward shifted profile can

also lead to bidirectional connections23, if potentiation dominates depression. The imbalance of the STDP profile in favor of potentiation in short spike-pairing times, may result in the

retention of bidirectional connections when the neurons are loosely phase-locked23. In a more realistic modeling, considering forward and backward propagation delays, we have previously

shown32 that the widely accepted consequences of conventional STDP, mentioned above, can be challenged. Here we showed that in this framework, the evolution of the bidirectional connections

and the symmetry of the emerging structure shows multistability and the degree of heterogeneity in the initial setting of the network determines the final structure of the network.

Experimentally observed pair-based STDP parameters have been shown to be unbalanced: A+ > A− and τ+ < τ−2,3,5. However, a balanced profile of STDP, i.e. \({A}_{+}\,=\,{A}_{-}\) and τ+ = τ−,

has widely been used in computational and theoretical studies4,19,20,21,23, since it can provide a suitable substrate for extracting the pure effect of other parameters, e.g. propagation

delays, on the dynamics of the system. For example, as noted above, in a potentiation dominated profile of STDP, bidirectional connections can emerge without incorporation of propagation

delays in the model23,31,35. In the present study we chose a balanced STDP profile to highlight the effects which can be directly attributed to propagation delays.

Previous studies ascribed the final stable connection regime in neuronal networks with synaptic plasticity without propagation delays to the initial mean coupling33,34. Here, based on the

analysis presented for the two-neuron motif, we focused on the multistability of the network structure due to the disparity of the initial synaptic strengths. Our results show that for every

pair of neurons, the final configuration of the synaptic connections follows a bistable dynamics governed by the initial mismatch of the strength of the synaptic connections in both

directions, where the initial asymmetry in the structure (difference in the synaptic strengths) specifies the final synaptic configuration. The emerging configurations depend on the

difference between dendritic and axonal delays: For larger dendritic delays, the final structures are unidirectional and bidirectional, while for larger axonal delays the two achievable

states are unidirectional or fully decoupled neurons. In particular, our results highlight the importance of propagation delays, which are usually neglected in modeling studies of STDP:

Without taking into account delays, the bistability cannot emerge, and all initial settings end up with a unidirectional configuration.

Our findings demonstrate the crucial role of the presence and the range of dendritic and axonal propagation delays in regulating the emergent structures of synaptic connections in plastic

excitatory neuronal networks. We show that connections with experimentally measured values of short-range delays41,42 and gamma band firing rates58 might be favorable for strong

bidirectional loops or unidirectional connections, depending on the initial distribution of the synaptic strengths (see Fig. 5). In contrast, in the case of long-range connections, a loosely

connected network or unidirectional synaptic structures might emerge (see Fig. 6). Therefore, the difference of dendritic and axonal propagation delays is crucial for the selection of the

network’s ultimately emerging coupling regimes. In this way, qualitatively distinct connectivity patterns may emerge.

The emergence of multistable coupling regimes can be of interest since such systems can be used in order to construct memory building blocks. Bistability of the synaptic strengths, arising

from the positive feedback nature of STDP, results in the emergence of different stable attractor states of the synaptic connections59. Switching between different stable attractors enables

neuronal networks to maintain and retrieve memories. Bistability of the network dynamics with recurrent connections mediated by STDP has been addressed for stationary13 or oscillatory

inputs60. Bistable dynamics can be characterized by the presence of two extreme stable fixed points of the synaptic strengths at gmin and gmax, imposed by the hard bound saturation

constraint.The choice of the saturation constraints can have significant effects on the final distribution of the synaptic strengths; however, it does not crucially affect the weight

dynamics61. Therefore, the main results presented in this study, i.e., development of different connectivity patterns can also be qualitatively obtained when soft bounds are imposed on the

synaptic strengths.

The dependence of the emergent structure to the firing rate of the neurons was experimentally observed58, showing that pairing of spikes with both positive and negative time differences

leads to potentiation in the high firing rate regime, which implicitly indicates that bidirectional connections can be promoted in this regime. While previous attempts with pair-based STDP

failed to reproduce these results, our study shows that this can be achieved by considering propagation delays without having to consider triplets of spikes in the formulation32. Here, we

showed that the domain of attraction for each achievable final configuration of the synapses depends on the firing frequency of the neurons. For low firing frequency, the two synapses in the

pairs of bidirectional connections evolve in different directions and unidirectional connections are more likely to emerge and survive in the network, as suggested by several studies on

STDP18,19,20,21,22,23. However, by increasing the firing frequency, the simultaneous potentiation or depression of the bidirectional connections becomes more probable, so that the measure of

the attraction domain for a symmetric configuration in the two dimensional space of the initial synaptic strengths expands. Accordingly, in recurrent neuronal networks the width of the

distribution of the synaptic strengths and the firing frequencies determine the emergent structure of the network and, in particular, the number of two-neuron loops in the final structure.

Furthermore, our results show that the symmetric depression of reciprocal connections between neurons in the phase-locked state is possible when favorable combinations of initial synaptic

strengths, range of firing rates, and propagation delays are met. We showed that by considering a non-zero lower hard bound gmin, the depression of reciprocal connections can be stabilized

in order to construct a loosely connected network, as predicted by our theoretical framework. The possibility of a symmetric stable depression of reciprocal connections in the phase-locked

mode may contribute to a further development of brain stimulation techniques that induce an anti-kindling, i.e., an unlearning of abnormally up-regulated synaptic connectivity and, in turn,

abnormal synchrony38. Coordinated reset (CR) stimulation62, a desynchronizing multisite stimulation technique was successfully tested in preclinical63,64 and clinical65,66,67 proof of

concept studies. However, our approach presented here, may lead to further improvements of brain stimulation techniques causing sustained therapeutic effects.

The neuronal oscillators are subjected to classic pair-based STDP rule where the synaptic strengths are modified based on the learning window function introduced in Eq. (2). The evolution of

the synaptic strengths by the pair-based STDP rule can be calculated by taking the average of Eq. (2) over a period of the spiking neuron and smoothing, \({\dot{g}}_{ij}\simeq {\rm{\Delta

}}{g}_{ij}/T\) (see Supplementary Fig. S1; for details on the interplay between the temporal scale of the parameters with STDP models see68), which is given

by:

}}t|)\,\exp \,(-\frac{|T-|\xi +{\rm{\Delta }}t||}{{\tau }_{\pm }})],\\ {\dot{g}}_{12}=\frac{{A}_{\pm }}{T}[{\rm{sgn}}(\xi -{\rm{\Delta }}t)\,\,\exp \,(-\frac{|\xi -{\rm{\Delta }}t|}{{\tau

}_{\pm }})+{\rm{sgn}}\,(T-|\xi -{\rm{\Delta }}t|)\,\exp \,(-\frac{|T-|\xi -{\rm{\Delta }}t||}{{\tau }_{\pm }})],\end{array}$$ (3)

where A+(A−) and τ+(τ−) are the rate and the effective time window of synaptic potentiation (depression), respectively. T is the period of spiking and sgn(Δt) is the sign function. In the

entire manuscript the profile of STDP is balanced by setting the parameters to A+ = A− = 0.005, and τ+ = τ− = 20 ms. Synaptic strengths are confined in the interval (gmin, gmax) = [0.05,1].

It should be noted that hard bounds are imposed on the allowed range of synaptic strengths: The synaptic strengths are set to gmin (gmax) once they cross the lower (upper) limit of their

allowed range.

Considering that the rate of synaptic change is small, and therefore, the changes in the synaptic strengths are negligible on the fast timescale of the system, the reduced averaged phase

model for weakly pulse-coupled neuronal oscillators characterized by intrinsic frequency ωi = 2πνi and infinitesimal phase sensitivity Z(φ) can be written as follows69,70:

}}_{i}={\omega }_{i}+\frac{1}{2\pi }\sum _{j\mathrm{=1,}j\ne i}^{N}{g}_{ij}\,Z(\psi +{\phi }_{i}-{\phi }_{j}),\,i,j\mathrm{=1,}\,\mathrm{2,}\,\ldots ,\,N,$$ (4)

where the neuronal oscillators are coupled via delayed connections of strength gij with total delay τ = τd + τa. φi is the phase of the i-th oscillator, ψ = ωiτ is the rescaled delay, and N

is the number of oscillators. The neurons fire every time their phase passes multiples of 2π. In the model, we ignore the synaptic processing time, but the results are not affected by this

assumption. Eq. (4) can be written for two coupled type-II phase oscillators with analytical phase response curve (PRC) Z(φ) = −sin(φ):

}_{1}-\frac{{g}_{12}}{2\pi }\,\sin (\psi +{\phi }_{1}-{\phi }_{2}),\\ {\dot{\phi }}_{2}={\omega }_{2}-\frac{{g}_{21}}{2\pi }\,\sin (\psi +{\phi }_{2}-{\phi }_{1}),\end{array}$$ (5)

where subtracting these two relations gives the evolution equation for the relative phase of the two neurons:

)-{g}_{21}\,\sin (\psi +\chi )],$$ (6)

where χ = φ2 − φ1 is the phase lag, and Ω = ω2 − ω1. Using the trigonometric identity sin(x ± y) = sinx cosy ± cosx siny, Eq. (6) can be rearranged to Eq. (1).

Joint Phase Model

In general, the fixed point of the phase lag \({\chi }_{i}^{\ast }\) of the Eq. (6) for type-I neuronal oscillator with analytical PRC function Z(ψ ± χ) = 1 − cos(ψ ± χ), is given

by:

\,\cos \,{\chi }_{1}^{\ast })}),\\ {\chi }_{2}^{\ast }=\pi -{\chi }_{1}^{\ast },\end{array}$$ (7)

where \({\chi }_{1}^{\ast }\) is the inphase firing solution and \({\chi }_{2}^{\ast }\) belongs to antiphase state. Given the synaptic strengths, only one of these fixed points are stable

in a given Ω and delay time ψ. The fixed points of type-II neuronal oscillator with analytical PRC function \(Z(\psi \pm \chi )=-\,\sin (\psi \pm \chi )\) can be derived

similarly:

\,{\chi }_{1}^{\ast })}),\\ {\chi }_{2}^{\ast }=\pi -{\chi }_{1}^{\ast }\mathrm{.}\end{array}$$ (8)

Eqs (7) and (8) show that the fixed points of both type-I and type-II neuronal oscillations are self-consistent in the presence of intrinsic frequency mismatch Ω between the two oscillators.

In this case, the stable fixed point \({\chi }_{i}^{\ast }\) is simply where the two \({y}_{1}={\chi }_{i}^{\ast }\) and \({y}_{2}={\tan }^{-1}(f(\psi ,{\chi }_{i}^{\ast }))\) curves

intersect. The other approach is to solve the equation \({\chi }_{i}^{\ast }-{\tan }^{-1}(f(\psi ,{\chi }_{i}^{\ast }))=0\) numerically using any root-finding scheme. However, without loss

of generality, one can assume that the intrinsic frequency mismatch between the two oscillators is negligible, i.e. \({\rm{\Omega }}\simeq 0\). Ignoring Ω, the type-I fixed point is still

self-consistent, but the type-II fixed point can be simplified to:

{\tan }^{-1}({\rm{\Gamma }}\,\tan \,\psi ),\,{\rm{\Gamma }}=|\frac{{g}_{12}-{g}_{21}}{{g}_{12}+{g}_{21}}|,\\ {\chi }_{2}^{\ast }=\pi -{\chi }_{1}^{\ast },\end{array}$$ (9)

where \({\rm{\Gamma }}\) is a positive expression that reflects the relative synaptic strength.

A fully connected recurrent excitatory network with N = 200 type-II neuronal phase oscillators were simulated in the high-frequency regime with ν = 80 Hz. In the network simulation, the

initial mean coupling is fixed at \(\bar{g}\)(0) = 0.5. The elements of the adjacency matrix A are multiplied by the corresponding array in the synaptic strength matrix G in order to

establish a weighted adjacency matrix AG. Note that the main diagonal arrays of the weighted adjacency matrix are zero since there is no self-loop in the network. Phase oscillators obey Eq.

(1) and the excitatory synapses are modified by the pair-based STDP profile according to Eq. (2). The phases of the oscillators are initially uniformly distributed between 0 and π. The

dendritic propagation delay is fixed at τd = 0.5 ms. STDP parameters are A+ = A− = 0.005, and τ+ = τ− = 20 ms. We also define an order parameter r(t) for the network of phase oscillators

ranging between 0 and 1 that measures the degree to which the system is synchronized71:

where Ψ(t) is the average phase and N is the number of neuronal oscillators.

A bidirectional connection corresponds to a closed loop of length 2 in a network of neurons. In order to measure the number of such closed loops, a directed graph is constructed.

Transformation of the synaptic strength matrix G, into a directed graph is performed by considering a threshold h = 0.2. Assuming that there are no self-loops, i.e. \({g}_{ii}=0\), the

corresponding value in the graph adjacency matrix M of the resultant directed graph is assigned to 1 when the synaptic strength is greater than h, and zero otherwise. The number of closed

loops of length 2 in the graph adjacency matrix M is then21,23:

where Tr denotes the matrix trace. In order to perform a better comparison, L2 is normalized to the total number of possible loops of the same length i.e. N(N − 1)/2, ignoring self-loops,

where N denotes the number of the neuronal phase oscillators or nodes in the network. Therefore, the resulted L2 is a normalized number between 0 and 1.

To quantify the proportion of unidirectional connections and discriminate asymmetric modification of the synapses from symmetric changes (either symmetric potentiation or symmetric

depression), we used another measure which has been introduced by Bayati and Valizadeh17. We first defined the synaptic cost of the network as the sum of all synaptic strengths in the

weighted adjacency matrix \({{\bf{A}}}_{{\bf{G}}}\), i.e. \(S={\sum }_{i,j}{a}_{ij}{g}_{ij}\), where aij and gij are the arrays of adjacency A and synaptic strength G matrices, respectively.

The asymmetry level of the connections between two neurons can be measured by calculating the quantity Cij = −Cji = aij gij − aji gji. The asymmetry index of the network can then be defined

as \({C}_{{\rm{net}}}\mathrm{=(1/}S){\sum }_{i > j}|{C}_{ij}|\). By definition, the network asymmetry index Cnet is scaled in the range [0,1]. In the case of a fully symmetric network, Cnet

 = 0, whereas in a fully asymmetric network, Cnet = 1.

All data generated or analysed during this study are included in this published article (and its Supplementary Information files).

References Gerstner, W., Kempter, R., van Hemmen, J. L. & Wagner, H. A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76 (1996).

Article  ADS  PubMed  CAS  Google Scholar 

Markram, H., Lübke, J., Frotscher, M. & Sakmann, B. Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science 275, 213–215 (1997).

Article  PubMed  CAS  Google Scholar 

Bi, G. Q. & Poo, M. M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. Journal of Neuroscience 18,

10464–10472 (1998).

Article  PubMed  CAS  Google Scholar 

Song, S., Miller, K. D. & Abbott, L. F. Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nature Neuroscience 3, 919–926 (2000).

Article  PubMed  CAS  Google Scholar 

Bi, G. Q. & Poo, M. M. Synaptic modification by correlated activity: Hebb’s postulate revisited. Annual Review of Neuroscience 24, 139–166 (2001).

Article  PubMed  CAS  Google Scholar 

Kempter, R., Gerstner, W. & van Hemmen, J. L. Intrinsic stabilization of output rates by spike-based hebbian learning. Neural Computation 13, 2709–2741 (2001).

Article  PubMed  MATH  CAS  Google Scholar 

Gütig, R., Aharonov, R., Rotter, S. & Sompolinsky, H. Learning input correlations through nonlinear temporally asymmetric hebbian plasticity. Journal of Neuroscience 23, 3697–3714 (2003).

Article  PubMed  Google Scholar 

Izhikevich, E. M., Gally, J. A. & Edelman, G. M. Spike-timing dynamics of neuronal groups. Cerebral Cortex 14, 933–944 (2004).

Article  PubMed  Google Scholar 

Morrison, A., Aertsen, A. & Diesmann, M. Spike-timing-dependent plasticity in balanced random networks. Neural Computation 19, 1437–1467 (2007).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A. & van Hemmen, J. L. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. i. input

selectivity–strengthening correlated input pathways. Biological Cybernetics 101, 81–102 (2009).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A. & van Hemmen, J. L. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. ii.

input selectivity–symmetry breaking. Biological Cybernetics 101, 103–114 (2009).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A. & van Hemmen, J. L. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. iii.

partially connected neurons driven by spontaneous activity. Biological Cybernetics 101, 411–426 (2009).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A. & van Hemmen, J. L. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. iv.

Biological Cybernetics 101, 427–444 (2009).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Gilson, M., Burkitt, A. N., Grayden, D. B., Thomas, D. A. & van Hemmen, J. L. Emergence of network structure due to spike-timing-dependent plasticity in recurrent neuronal networks. v.

self-organization schemes and weight dependence. Biological Cybernetics 103, 365–386 (2010).

Article  MathSciNet  PubMed  Google Scholar 

Gilson, M., Burkitt, A. & van Hemmen, L. J. Stdp in recurrent neuronal networks. Frontiers in Computational Neuroscience 4, 1–15 (2010).

Article  Google Scholar 

Mikkelsen, K., Imparato, A. & Torcini, A. Emergence of slow collective oscillations in neural networks with spike-timing dependent plasticity. Physical Review Letters 110, 208101 (2013).

Article  ADS  PubMed  CAS  Google Scholar 

Bayati, M. & Valizadeh, A. Effect of synaptic plasticity on the structure and dynamics of disordered networks of coupled neurons. Physical Review E 86, 011925 (2012).

Article  ADS  CAS  Google Scholar 

Abbott, L. F. & Nelson, S. B. Synaptic plasticity: taming the beast. Nature Neuroscience 3, 1178–1183 (2000).

Article  PubMed  CAS  Google Scholar 

Song, S. & Abbott, L. F. Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350 (2001).

Article  PubMed  CAS  Google Scholar 

Lubenov, E. V. & Siapas, A. G. Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131 (2008).

Article  PubMed  CAS  Google Scholar 

Kozloski, J. & Cecchi, G. A. A theory of loop formation and elimination by spike timing-dependent plasticity. Frontiers in Neural Circuits 4, 1–11 (2010).

Google Scholar 

Knoblauch, A., Hauser, F., Gewaltig, M.-O., Körner, E. & Palm, G. Does spike-timing-dependent synaptic plasticity couple or decouple neurons firing in synchrony? Frontiers in Computational

Neuroscience 6, 1–27 (2012).

Article  Google Scholar 

Babadi, B. & Abbott, L. F. Pairwise analysis can account for network structures arising from spike-timing dependent plasticity. PLoS Computational Biology 9, e1002906 (2013).

Article  ADS  MathSciNet  PubMed  PubMed Central  CAS  Google Scholar 

Karbowski, J. & Ermentrout, G. B. Synchrony arising from a balanced synaptic plasticity in a network of heterogeneous neural oscillators. Physical Review E 65, 031902 (2002).

Article  ADS  MathSciNet  CAS  Google Scholar 

Masuda, N. & Kori, H. Formation of feedforward networks and frequency synchrony by spike-timing-dependent plasticity. Journal of Computational Neuroscience 22, 327–345 (2007).

Article  MathSciNet  PubMed  Google Scholar 

Goldman-Rakic, P. S. Development of cortical circuitry and cognitive function. Child Development 58, 601–622 (1987).

Article  PubMed  CAS  Google Scholar 

Markram, H., Lübke, J., Frotscher, M., Roth, A. & Sakmann, B. Physiology and anatomy of synaptic connections between thick tufted pyramidal neurones in the developing rat neocortex. The

Journal of Physiology 500, 409–440 (1997).

Article  PubMed  PubMed Central  CAS  Google Scholar 

Song, S., Sjöström, P. J., Reigl, M., Nelson, S. & Chklovskii, D. B. Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biology 3, e68 (2005).

Article  PubMed  PubMed Central  CAS  Google Scholar 

Morishima, M. & Kawaguchi, Y. Recurrent connection patterns of corticostriatal pyramidal cells in frontal cortex. Journal of Neuroscience 26, 4394–4405 (2006).

Article  PubMed  CAS  Google Scholar 

Douglas, R. J. & Martin, K. A. Recurrent neuronal circuits in the neocortex. Current Biology 17, R496–R500 (2007).

Article  PubMed  CAS  Google Scholar 

Lücken, L., Popovych, O. V., Tass, P. A. & Yanchuk, S. Noise-enhanced coupling between two oscillators with long-term plasticity. Physical Review E 93, 032210 (2016).

Article  ADS  MathSciNet  PubMed  CAS  Google Scholar 

Madadi Asl, M., Valizadeh, A. & Tass, P. A. Dendritic and axonal propagation delays determine emergent structures of neuronal networks with plastic synapses. Scientific Reports 7, 39682

(2017).

Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

Maistrenko, Y. L., Lysyansky, B., Hauptmann, C., Burylko, O. & Tass, P. A. Multistability in the kuramoto model with synaptic plasticity. Physical Review E 75, 066207 (2007).

Article  ADS  MathSciNet  CAS  Google Scholar 

Popovych, O. V. & Tass, P. A. Desynchronizing electrical and sensory coordinated reset neuromodulation. Frontiers in Human Neuroscience 6, 1–14 (2012).

Article  Google Scholar 

Popovych, O. V., Yanchuk, S. & Tass, P. A. Self-organized noise resistance of oscillatory neural networks with spike timing-dependent plasticity. Scientific Reports 3, 2926 (2013).

Article  ADS  PubMed  PubMed Central  Google Scholar 

Popovych, O. V. & Tass, P. A. Control of abnormal synchronization in neurological disorders. Frontiers in Neurology 5, 1–12 (2014).

Article  Google Scholar 

Tass, P. A. Vibrotactile coordinated reset stimulation for the treatment of neurological diseases: Concepts and device specifications. Cureus 9, 1–16 (2017).

Google Scholar 

Tass, P. A. & Majtanik, M. Long-term anti-kindling effects of desynchronizing brain stimulation: a theoretical study. Biological Cybernetics 94, 58–66 (2006).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Agmon-Snir, H. & Segev, I. Signal delay and input synchronization in passive dendritic structures. Journal of Neurophysiology 70, 2066–2085 (1993).

Article  PubMed  CAS  Google Scholar 

Schierwagen, A. & Claus, C. Dendritic morphology and signal delay in superior colliculus neurons. Neurocomputing 38, 343–350 (2001).

Article  Google Scholar 

Cleland, B., Levick, W., Morstyn, R. & Wagner, H. Lateral geniculate relay of slowly conducting retinal afferents to cat visual cortex. The Journal of Physiology 255, 299–320 (1976).

Article  PubMed  PubMed Central  CAS  Google Scholar 

Swadlow, H. A. & Weyand, T. G. Corticogeniculate neurons, corticotectal neurons, and suspected interneurons in visual cortex of awake rabbits: receptive-field properties, axonal properties,

and effects of eeg arousal. Journal of Neurophysiology 57, 977–1001 (1987).

Article  PubMed  CAS  Google Scholar 

Swadlow, H. A. Efferent neurons and suspected interneurons in s-1 forelimb representation of the awake rabbit: receptive fields and axonal properties. Journal of Neurophysiology 63,

1477–1498 (1990).

Article  PubMed  CAS  Google Scholar 

Ernst, U., Pawelzik, K. & Geisel, T. Synchronization induced by temporal delays in pulse-coupled oscillators. Physical Review Letters 74, 1570–1573 (1995).

Article  ADS  PubMed  CAS  Google Scholar 

Ermentrout, B., Pascal, M. & Gutkin, B. The effects of spike frequency adaptation and negative feedback on the synchronization of neural oscillators. Neural Computation 13, 1285–1310 (2001).

Article  PubMed  MATH  CAS  Google Scholar 

Sadeghi, S. & Valizadeh, A. Synchronization of delayed coupled neurons in presence of inhomogeneity. Journal of Computational Neuroscience 36, 55–66 (2014).

Article  MathSciNet  PubMed  MATH  CAS  Google Scholar 

Esfahani, Z. G., Gollo, L. L. & Valizadeh, A. Stimulus-dependent synchronization in delayed-coupled neuronal networks. Scientific Reports 6, 23471 (2016).

Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

Ermentrout, B. Type i membranes, phase resetting curves, and synchrony. Neural Computation 8, 979–1001 (1996).

Article  PubMed  CAS  Google Scholar 

Achuthan, S. & Canavier, C. C. Phase-resetting curves determine synchronization, phase locking, and clustering in networks of neural oscillators. Journal of Neuroscience 29, 5218–5233

(2009).

Article  PubMed  CAS  Google Scholar 

Câteau, H., Kitano, K. & Fukai, T. Interplay between a phase response curve and spike-timing-dependent plasticity leading to wireless clustering. Physical Review E 77, 051909 (2008).

Article  ADS  CAS  Google Scholar 

Kempter, R., Gerstner, W. & Van Hemmen, J. L. Hebbian learning and spiking neurons. Physical Review E 59, 4498 (1999).

Article  ADS  MathSciNet  CAS  Google Scholar 

Aoki, T. & Aoyagi, T. Co-evolution of phases and connection strengths in a network of phase oscillators. Physical Review Letters 102, 034101 (2009).

Article  ADS  PubMed  CAS  Google Scholar 

Pariz, A. et al. High frequency neurons determine effective connectivity in neuronal networks. NeuroImage 166, 349–359 (2018).

Article  PubMed  Google Scholar 

Zeitler, M. & Tass, P. A. Augmented brain function by coordinated reset stimulation with slowly varying sequences. Frontiers in Systems Neuroscience 9, 1–11 (2015).

Article  ADS  Google Scholar 

Zeitler, M. & Tass, P. A. Anti-kindling induced by two-stage coordinated reset stimulation with weak onset intensity. Frontiers in Computational Neuroscience 10, 1–22 (2016).

Article  Google Scholar 

Bayati, M., Valizadeh, A., Abbassian, A. & Cheng, S. Self-organization of synchronous activity propagation in neuronal networks driven by local excitation. Frontiers in Computational

Neuroscience 9, 1–15 (2015).

Article  Google Scholar 

Pfister, J. P. & Gerstner, W. Triplets of spikes in a model of spike timing-dependent plasticity. Journal of Neuroscience 26, 9673–9682 (2006).

Article  PubMed  CAS  Google Scholar 

Sjöström, P. J., Turrigiano, G. G. & Nelson, S. B. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164 (2001).

Article  PubMed  Google Scholar 

Chaudhuri, R. & Fiete, I. Computational principles of memory. Nature Neuroscience 19, 394–403 (2016).

Article  PubMed  CAS  Google Scholar 

Pfister, J. P. & Tass, P. Stdp in oscillatory recurrent networks: theoretical conditions for desynchronization and applications to deep brain stimulation. Frontiers in Computational

Neuroscience 4, 1–10 (2010).

Google Scholar 

Morrison, A., Diesmann, M. & Gerstner, W. Phenomenological models of synaptic plasticity based on spike timing. Biological Cybernetics 98, 459–478 (2008).

Article  MathSciNet  PubMed  PubMed Central  MATH  Google Scholar 

Tass, P. A. A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biological Cybernetics 89, 81–88 (2003).

Article  PubMed  MATH  Google Scholar 

Tass, P. A. et al. Coordinated reset has sustained aftereffects in parkinsonian monkeys. Annals of Neurology 72, 816–820 (2012).

Article  PubMed  Google Scholar 

Wang, J. et al. Coordinated reset deep brain stimulation of subthalamic nucleus produces long-lasting, dose-dependent motor improvements in the 1-methyl-4-phenyl-1, 2, 3,

6-tetrahydropyridine non-human primate model of parkinsonism. Brain Stimulation: Basic, Translational, and Clinical Research in Neuromodulation 9, 609–617 (2016).

Article  Google Scholar 

Tass, P. A., Adamchic, I., Freund, H. J., von Stackelberg, T. & Hauptmann, C. Counteracting tinnitus by acoustic coordinated reset neuromodulation. Restorative Neurology and Neuroscience 30,

137–159 (2012).

PubMed  Google Scholar 

Adamchic, I. et al. Coordinated reset neuromodulation for parkinson’s disease: Proof-of-concept study. Movement Disorders 29, 1679–1684 (2014).

Article  PubMed  PubMed Central  Google Scholar 

Syrkin-Nikolau, J. et al. Coordinated reset vibrotactile stimulation shows prolonged improvement in parkinson’s disease. Movement Disorders 33, 179–180 (2018).

Article  PubMed  Google Scholar 

Gilson, M., Bürck, M., Burkitt, A. N. & van Hemmen, J. L. Frequency selectivity emerging from spike-timing-dependent plasticity. Neural Computation 24, 2251–2279 (2012).

Article  MathSciNet  PubMed  MATH  Google Scholar 

Izhikevich, E. M. Weakly pulse-coupled oscillators, fm interactions, synchronization, and oscillatory associative memory. IEEE Transactions on Neural Networks 10, 508–526 (1999).

Article  PubMed  CAS  Google Scholar 

Hoppensteadt, F. C. & Izhikevich, E. M. Weakly connected neural networks (Springer Science & Business Media, 1997).

Kuramoto, Y. Chemical oscillations, waves, and turbulence (Springer Science & Business Media, 1984).

Download references

The study was funded by the John A. Blume Foundation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

Author informationAuthors and Affiliations Department of Physics, Institute for Advanced Studies in Basic Sciences (IASBS), Zanjan, 45195-1159, Iran

Mojtaba Madadi Asl & Alireza Valizadeh

School of Cognitive Sciences, Institute for Research in Fundamental Sciences (IPM), Tehran, 19395-5746, Iran

Alireza Valizadeh

Department of Neurosurgery, School of Medicine, Stanford University, Stanford, CA, 94305, USA

Peter A. Tass

AuthorsMojtaba Madadi AslView author publications You can also search for this author inPubMed Google Scholar

Alireza ValizadehView author publications You can also search for this author inPubMed Google Scholar

Peter A. TassView author publications You can also search for this author inPubMed Google Scholar

A.V. and P.A.T. conceived the study, M.M.A. conducted the numerical simulations and theoretical approximations, M.M.A., A.V. and P.A.T. analysed the results. M.M.A., A.V. and P.A.T. wrote

and reviewed the paper.

Corresponding author Correspondence to Alireza Valizadeh.

The authors declare no competing interests.

Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

InformationRights and permissions

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or

other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.

Reprints and permissions

About this articleCite this article Madadi Asl, M., Valizadeh, A. & Tass, P.A. Delay-Induced Multistability and Loop Formation in Neuronal Networks with Spike-Timing-Dependent Plasticity.

Sci Rep 8, 12068 (2018). https://doi.org/10.1038/s41598-018-30565-9

Download citation

Received: 16 March 2018

Accepted: 02 August 2018

Published: 13 August 2018

DOI: https://doi.org/10.1038/s41598-018-30565-9

Share this article Anyone you share the following link with will be able to read this content:

Get shareable link Sorry, a shareable link is not currently available for this article.

Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative