Reader TTS

ABSTRACT The stress of a fluid on a confining wall is given by the mechanical wall forces, independent of the nature of the fluid being passive or active. At thermal equilibrium, an equation

of state exists and stress is likewise obtained from intrinsic bulk properties; even more, stress can be calculated locally. Comparable local descriptions for active systems require a

particular consideration of active forces. Here, we derive expressions for the stress exerted on a local volume of a systems of spherical active Brownian particles (ABPs). Using the virial

theorem, we obtain two identical stress expressions, a stress due to momentum flux across a hypothetical plane, and a bulk stress inside of the local volume. In the first case, we obtain an

active contribution to momentum transport in analogy to momentum transport in an underdamped passive system, and we introduce an active momentum. In the second case, a generally valid

expression for the swim stress is derived. By simulations, we demonstrate that the local bulk stress is identical to the wall stress of a confined system for both, non-interacting ABPs as

well as ABPs with excluded-volume interactions. This underlines the existence of an equation of state for a system of spherical ABPs. Most importantly, our calculations demonstrated that

active stress is not a wall (boundary) effect, but is caused by momentum transport. We demonstrate that the derived stress expression permits the calculation of the local stress in

inhomogeneous systems of ABPs. SIMILAR CONTENT BEING VIEWED BY OTHERS DEPENDENCY OF ACTIVE PRESSURE AND EQUATION OF STATE ON STIFFNESS OF WALL Article Open access 12 November 2021 FROM A

MICROSCOPIC INERTIAL ACTIVE MATTER MODEL TO THE SCHRÖDINGER EQUATION Article Open access 09 March 2023 TWO-DIMENSIONAL BROWNIAN MOTION OF ACTIVE PARTICLE ON SUPERFLUID HELIUM SURFACE Article

Open access 18 December 2023 INTRODUCTION The agents of active matter perpetually convert internal energy or energy from the environment into systematic translational motion and are, thus,

usually far from thermal equilibrium1,2,3,4,5. Their motility gives rise to remarkable phenomena such as collective motion, activity-induced phase

transitions5,6,7,8,9,10,11,12,13,14,15,16,17, or wall accumulation18,19,20,21. Activity is associated with the generation of active stresses, which are responsible for the persistent

nonequilibrium state of a system22,23,24. Such stresses are particularly interesting, since there is no equilibrium counterpart and thus, they usually cannot be described by equilibrium

thermodynamics. An expression for the active pressure in systems of active Brownian particles (ABPs), based on a generalization of the virial including the active force, has been introduced

recently22,23. Subsequently, expressions for the active pressure have been derived in various ways for both, the overdamped dynamics of ABPs25,26,27,28,29 as well as in presence of

inertia30,31. Mechanical stress/pressure as force per area can be defined even far from equilibrium. The fundamental question is then, how this mechanical pressure is related to

nonequilibrium thermodynamics. As a step toward such a relation, the existence of an equation of state for systems of ABPs has been addressed24,28,32. Various simulation and theoretical

studies confirm that indeed such a relation, including the active pressure, exists for spherical ABPs22,23,24,25,32,33,34. However, for (anisotropic) active particles which experience a

torque, pressure is in general not a state function anymore28,35. A pressure equation of state implies equivalence of wall and local pressure at any point inside the homogeneous relevant

volume. Exactly this identity has been questioned in ref.27. Typically, confined or periodic systems are considered and relations between wall forces, hence the wall pressure, and virial,

including the active-force virial, are determined22,23,25,28, but no local (bulk) pressure is calculated. Aside from ref.27, local pressure and the existence of an equation of state has been

addressed in ref.36. In this article, we derive an instantaneous expression for the local stress (pressure) in a system of spherical active Brownian particles using the virial approach.

Thereby, we follow the strategy of ref.37 for passive systems. A volume Δ_V_ within a larger volume _V_ is considered and an expression is derived for the pressure inside Δ_V_. Considering

the equations of motions of the ABPs inside the volume Δ_V_, including inertia, we obtain the well-known virial expressions for the pressure of a passive system. In addition, however, we

find contributions by activity. On the one hand, we obtain a virial expression for the active stress (swim stress) of particles inside Δ_V_, which differs from the swim stress discussed so

far, and, on the other hand, we find an original momentum-flux contribution of APBs to stress, which we denote as active momentum. The notation rests upon the similarity to the classical

linear momentum of a passive particle. It is precisely this term, which distinguishes our studies from those of ref.27. In general, we agree with the arguments presented in ref.27, however,

the momentum flux across a plane in the system, similar to the momentum flux by inertia, yields an extra contribution to the local stress which is not considered in ref.27. In fact, in

ref.36 an “active impulse, defined as the mean momentum a particle will receive on average from the substrate in the future”, is introduce, resembling our instantaneous active momentum, but

the meaning is different. By computer simulations of non-interacting ABPs and ABPs interacting by a Lennard-Jones potential, we demonstrate that the derived expressions for the wall and bulk

stress are identical. This highlights the existence of a pressure equation state for spherical ABP systems22,24,36. Moreover, it opens up the possibility to calculate stresses locally, even

in inhomogeneous systems, which we confirm by calculating the local stress in a phase separated system. STRESS IN ACTIVE SYSTEMS MODEL We consider a system of _N_ ABPs of diameter _σ_ in a

three-dimensional volume _V_. Their equations of motion, including the inertia contribution, are given by $${m}{\mathop{{\boldsymbol{r}}}\limits^{\dot \dot }}_{{i}}+\gamma

{\dot{{\boldsymbol{r}}}}_{i}(t)=\gamma {v}_{0}{{\boldsymbol{e}}}_{i}(t)+{{\boldsymbol{F}}}_{i}(t)+{{\boldsymbol{\Gamma }}}_{i}(t),$$ (1) where _R__i_, \({\dot{{\boldsymbol{r}}}}_{i}\), and

_F__i_ (_i_ = 1, …, _N_) denote the particle positions, velocities, and forces, respectively, _m_ is the mass, _γ_ the translational friction coefficient, and _Γ__i_ are Gaussian white-noise

random forces, with the moments $$\langle {{\boldsymbol{\Gamma }}}_{i}(t)\rangle =\mathrm{0,}\,\langle {\Gamma }_{i\alpha }(t){\Gamma }_{j\beta }(t^{\prime} )\rangle =2\gamma

{k}_{B}T{\delta }_{\alpha \beta }{\delta }_{ij}\delta (t-t^{\prime} \mathrm{).}$$ (2) Here, _T_ denotes the temperature, _k__B_ the Boltzmann constant, and _α_, _β_ ∈ {_x_, _y_, _z_} the

Cartesian coordinate directions. A particle _i_ is propelled with constant velocity _v_0 along its orientation vector _E__i_. The latter changes in a diffusive manner according to

$${\dot{{\boldsymbol{e}}}}_{i}(t)={{\boldsymbol{\eta }}}_{i}(t)\times {{\boldsymbol{e}}}_{i}(t)-2{D}_{R}{{\boldsymbol{e}}}_{i}$$ (3) within the Ito interpretation of the multiplicative noise

process38; _Η__i_ is a Gaussian and Markovian stochastic process, with the moments $$\langle {\eta }_{i\alpha }(t)\rangle =\mathrm{0,}\,\langle {\eta }_{i\alpha }(t){\eta }_{j\beta

}(t^{\prime} )\rangle ={\gamma }_{R}{\delta }_{\alpha \beta }{\delta }_{ij}\delta (t-t^{\prime} \mathrm{).}$$ (4) The damping factor _γ__R_ is related to the rotational diffusion

coefficient, _D__R_, via _γ__R_ = 2_D__R_. Alternatively, the velocity equation of motion of an active Ornstein-Uhlenbeck particle can be considered39,40, where aside from the orientation

also the magnitude of the propulsion velocity is changing. In any case, the correlation function for the active velocity \({{\boldsymbol{v}}}_{i}^{(a)}={v}_{0}{{\boldsymbol{e}}}_{i}\)

is25,39 $$\langle {{\boldsymbol{v}}}_{i}^{(a)}(t)\cdot {{\boldsymbol{v}}}_{i}^{(a)}\mathrm{(0)}\rangle ={v}_{0}^{2}\langle {{\boldsymbol{e}}}_{i}(t)\cdot

{{\boldsymbol{e}}}_{i}\mathrm{(0)}\rangle ={v}_{0}^{2}{e}^{-{\gamma }_{R}t}.$$ (5) The forces _F__i_ include contributions from (short-range) interactions with confining walls,

\({{\boldsymbol{F}}}_{i}^{(w)}\), as well as possible pair-wise ABP interactions, _F__ij_, such that (the prime at the sum indicates that the index _j_ = _i_ is excluded)

$${{\boldsymbol{F}}}_{i}={{\boldsymbol{F}}}_{i}^{(w)}+\underset{j=1}{\overset{N}{\sum ^{\prime} }}{{\boldsymbol{F}}}_{ij}.$$ (6) GLOBAL STRESS IN CONFINED SYSTEM We examine now ABPs confined

in a rectangle (2D) or cuboid (3D) with walls located at ±_L__α_/2. The virial expression for the stress follows by multiplying the respective individual Cartesian equations of Eq. (1) by

_r__iα_, which yields25,41 $$\frac{d}{dt}[m\langle {\dot{r}}_{i\alpha }{r}_{i\alpha }\rangle +\frac{\gamma }{2}\langle {r}_{i\alpha }^{2}\rangle ]=m\langle {\dot{r}}_{i\alpha }^{2}\rangle

+\gamma \langle {v}_{i\alpha }^{(a)}{r}_{i\alpha }\rangle +\langle {F}_{i\alpha }^{(w)}{r}_{i\alpha }\rangle +\underset{j\mathrm{=1}}{\overset{N}{\sum ^{\prime} }}\langle {F}_{ij\alpha

}{r}_{i\alpha }\rangle ,$$ (7) where 〈…〉 denotes either a time or an ensemble average. Due to confinement, the left-hand side of Eq. (7) vanishes. With the definition of an external stress

\({\sigma }_{\alpha \alpha }^{(e)}\) as average total force exerted on a wall, $$V{\sigma }_{\alpha \alpha }^{(e)}=\sum _{i=1}^{N}\,\langle {F}_{i\alpha }^{(w)}{S}_{i\alpha }\rangle ,$$ (8)

where _S__iα_ = ±_L__α_/2 denotes the location of the wall with which particle _i_ interacts, Eq. (7) yields the equivalent internal stress $$V{\sigma }_{\alpha \alpha }^{(i)}=-\,\sum

_{i=1}^{N}\,m\langle {\dot{r}}_{i\alpha }^{2}\rangle -\sum _{i=1}^{N}\,\gamma \langle {v}_{i\alpha }^{(a)}{r}_{i\alpha }\rangle -\sum _{i=1}^{N}\,\langle {F}_{i\alpha }^{(w)}({r}_{i\alpha

}-{S}_{i\alpha })\rangle -\frac{1}{2}\sum _{i=1}^{N}\underset{j=1}{\overset{N}{\sum ^{\prime} }}\langle {F}_{ij\alpha }{r}_{ij\alpha }\rangle ,$$ (9) with _R__ij_ = _R__i_ − _R__j_, as sum

over all particles of the confined system. Hence, we denote this expression as global (wall) stress. Note that by definition \({\sigma }_{\alpha \alpha }^{(e)}={\sigma }_{\alpha \alpha

}^{(i)}\). The contribution with the active force is denoted as swim stress22,25,42 $$V{\sigma }_{\alpha \alpha }^{(s)}=-\,\sum _{i=1}^{N}\,\gamma \langle {v}_{i\alpha }^{(a)}{r}_{i\alpha

}\rangle \mathrm{.}$$ (10) The pressure itself follows as \({p}^{(i,e)}=-\,({\sum }_{\alpha }{\sigma }_{\alpha \alpha }^{(i,e)})/3\), where (_i_, _e_) refers either to the internal or

external pressure or stress. Aside from the wall term with the forces \({{\boldsymbol{F}}}_{i}^{(w)}\), the stress tensor (9) is identical with that derived in ref.25. The wall term captures

the finite range of the wall force and vanishes in the limit of vanishing wall interaction range. LOCAL VIRIAL AND LOCAL STRESS In order to determine the local stress at the position _R_

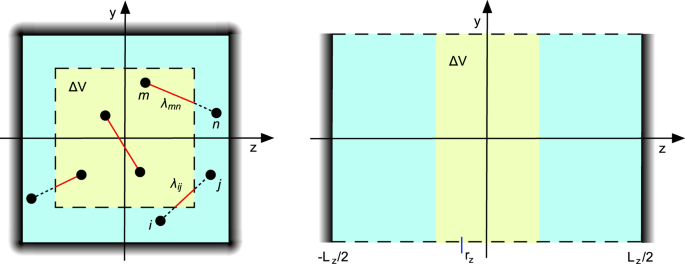
within the volume _V_, we consider a cuboidal subvolume Δ_V_ = Δ_L__x_ × Δ_L__y_ × Δ_L__z_ centered around _R_, with the side lengths Δ_L__α_ (cf. Fig. 1). ABPs inside of Δ_V_ interact with

each other as well as ABPs outside. Moreover, ABPs enter and leave Δ_V_ in the course of time. The internal stress follows from the suitable virial expression of ABPs inside of Δ_V_. To

derive the virial expression, as before, we multiply the equations (1) and (3) by _r__iα_, an additional factor Λ_iα_(_R_), and sum over all particles. The factor Λ_iα_ determines the volume

Δ_V_ − Λ_iα_(_R_) is unity when particle _i_ is within Δ_V_ in the coordinate direction _α_ and zero otherwise37. As a result, averaging yields $$\sum _{i=1}^{N}\,m\langle

{\dot{r}}_{i}^{2}{{\rm{\Lambda }}}_{i}\rangle +\sum _{i=1}^{N}\,m\langle {\dot{r}}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle +\sum _{i=1}^{N}\,\langle {F}_{i}{r}_{i}{{\rm{\Lambda

}}}_{i}\rangle +\sum _{i=1}^{N}\,\langle {{\rm{\Gamma }}}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle +\gamma \sum _{i=1}^{N}\,\langle {v}_{i}^{(a)}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle =0,$$ (11)

$$\sum _{i=1}^{N}\,\langle {e}_{i}{\dot{r}}_{i}{{\rm{\Lambda }}}_{i}\rangle +\sum _{i=1}^{N}\,\langle {e}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle -{\gamma }_{R}\sum _{i=1}^{N}\,\langle

{e}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle =\mathrm{0,}$$ (12) with the Ito interpretation of the colored noise process for _E_25,43, and the relations $$\frac{d}{dt}\langle

{\dot{r}}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle =\langle {\ddot{r}}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle +\langle {\dot{r}}_{i}^{2}{{\rm{\Lambda }}}_{i}\rangle +\langle

{\dot{r}}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle ,\,\frac{d}{dt}\langle {e}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle =\langle {\dot{e}}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle +\langle

e{\dot{r}}_{i}{{\rm{\Lambda }}}_{i}\rangle +\langle {e}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle \mathrm{.}$$ (13) Here, and in the following, we often suppress the index _α_ for

compactness of the expressions. Due to confinement, the left-hand sides of Eq. (13) vanish. Similarly, the averages \(\langle {\dot{r}}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle =\langle

{r}_{i}^{2}{\dot{{\rm{\Lambda }}}}_{i}\rangle =0\). Inserting the third term of Eq. (12) into Eq. (11), we obtain the virial expression $$\sum _{i\mathrm{=1}}^{N}\,m\langle

{\dot{r}}_{i}^{2}{{\rm{\Lambda }}}_{i}\rangle +\sum _{i\mathrm{=1}}^{N}\,m\langle {\dot{r}}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle +\sum _{i\mathrm{=1}}^{N}\,\langle

{F}_{i}{r}_{i}{{\rm{\Lambda }}}_{i}\rangle +\frac{\gamma }{{\gamma }_{R}}[\sum _{i\mathrm{=1}}^{N}\,\langle {v}_{i}^{(a)}{\dot{r}}_{i}{{\rm{\Lambda }}}_{i}\rangle +\sum

_{i\mathrm{=1}}^{N}\,\langle {v}_{i}^{(a)}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle ]=0.$$ (14) Here, we neglect terms with the averages 〈Γ_i__r__i_Λ_i_〉; these averages vanish as long as

inertia (cf. Eq. (1)) is taken into account. For an overdamped dynamics, _m_ = 0 in Eq. (1), 〈Γ_i__r__i_Λ_i_〉 yields the thermal contribution to the stress25. For passive systems with _v_0 =

 0, Eq. (14) reduces to the local virial expression in thermal equilibrium presented in ref.37. Compared to the global virial25, additional terms with the derivative of Λ_i_,

\({\dot{{\rm{\Lambda }}}}_{i}\), appear due to particles entering and leaving the local volume Δ_V_. Most remarkably, activity yields a similar contribution as inertia, namely \(\gamma {\sum

}_{i}\,\langle {v}_{i\alpha }^{(a)}{r}_{i\alpha }{\dot{{\rm{\Lambda }}}}_{i}\rangle /{\gamma }_{R}\), compared to \({\sum }_{i}\,\langle m{\dot{r}}_{i\alpha }{r}_{i\alpha

}{\dot{{\rm{\Lambda }}}}_{i}\rangle \). This demonstrates that transport of ABPs across a plane yields a contribution to stress similarly to the momentum

\({{\boldsymbol{p}}}_{i}^{(m)}=m{\dot{{\boldsymbol{r}}}}_{i}\) of a (passive) particle, in contrast to previous statements27. Hence, we can consider

$${{\boldsymbol{p}}}_{i}^{(a)}=\frac{\gamma }{{\gamma }_{R}}{{\boldsymbol{v}}}_{i}^{(a)}$$ (15) as an instantaneous active momentum. Formally, an analogous momentum (impulse) has been

introduced in ref.36 “as momentum the active particle will receive on average from its active force in the future”, thus, the meaning is rather different. Equation (14) includes volume and

boundary contributions, where terms with \({\dot{{\rm{\Lambda }}}}_{i}\) are pure boundary terms. Following the procedure of ref.37, the following external, \({\sigma }_{\alpha \alpha

}^{(e)}\), and internal, \({\sigma }_{\alpha \alpha }^{(i)}\), stress tensor components are identified, $$\begin{array}{c}{\rm{\Delta }}V{\sigma }_{\alpha \alpha }^{(e)}=\sum

_{i=1}^{N}\,m\langle {\dot{r}}_{i}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle +\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle {v}_{i}^{(a)}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle

+\sum _{i=1}^{N}\,\sum _{j=1}^{N}\langle ({r}_{i}-{\lambda }_{ij}{r}_{ij}){F}_{ij}{{\rm{\Lambda }}}_{i}\mathrm{(1}-{{\rm{\Lambda }}}_{j})\rangle \\ \,\,\,\,-\sum _{i=1}^{N}\,\sum

_{j=1}^{N}\,\langle {\lambda }_{ij}{r}_{ij}{F}_{ij}\mathrm{(1}-{{\rm{\Lambda }}}_{i}\mathrm{)(1}-{{\rm{\Lambda }}}_{j})\rangle ,\end{array}$$ (16) $${\rm{\Delta }}V{\sigma }_{\alpha \alpha

}^{(i)}=-\,\sum _{i=1}^{N}\,m\langle {\dot{r}}_{i}^{2}{{\rm{\Lambda }}}_{i}\rangle -\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle {v}_{i}^{(a)}{\dot{r}}_{i}{{\rm{\Lambda

}}}_{i}\rangle -\frac{1}{2}\sum _{i=1}^{N}\,\underset{j=1}{\overset{N}{\sum ^{\prime} }}\langle {\lambda }_{ij}{r}_{ij}{F}_{ij}\rangle \mathrm{.}$$ (17) Here, we assume that the volume Δ_V_

is sufficiently far from the surface, and, hence, short-range wall forces do not contribute to the local stress in Δ_V_. The external stress tensor \({\sigma }_{\alpha \alpha }^{(e)}\)

includes contributions by momentum flux across the boundary, with the active flux \(\gamma {\sum }_{i=1}^{N}\,\langle {v}_{i}^{(a)}{r}_{i}{\dot{{\rm{\Lambda }}}}_{i}\rangle /{\gamma }_{R}\),

as well as boundary force terms; the third term on the right-hand side of Eq. (16) accounts for stress contributions by forces between particles _i_ inside and _j_ outside of Δ_V_, and the

fourth term for force contributions, when all particles are outside of Δ_V_, but the connecting line intersects the volume Δ_V_; _λ__ij_ denotes the fraction of the line connecting particle

_i_ and _j_ inside of the volume Δ_V_ (cf. Fig. 1)37. Note, by suppression of the averages, instantaneous stresses are obtained. The internal stress tensor \({\sigma }_{\alpha \alpha

}^{(i)}\) (17) includes kinetic contributions from inertia and activity of particles, which are inside the volume of interest, as well as interparticle forces. The interparticle-force term

$${\rm{\Delta }}V{\sigma }_{\alpha \alpha }^{(if)}=-\,\frac{1}{2}\sum _{i=1}^{N}\,\underset{j=1}{\overset{N}{\sum ^{\prime} }}\langle {\lambda }_{ij}{r}_{ij}{F}_{ij}\rangle $$ (18) includes

contributions from particles both, inside of Δ_V_, here _λ__ij_ = 1—this is the standard volume term—, as well as combinations, where a particle is inside and all others, within the finite

interaction range, are outside, or both are outside, but their connecting line intersects the volume Δ_V_, here _λ__ij_ < 1. The latter are boundary terms in analogy to the wall

contributions in Eq. (9) of the global system with finite-range wall forces41. Remarkably, a new expression for the swim stress is obtained $${\rm{\Delta }}V{\sigma }_{\alpha \alpha

}^{(s)}=-\,\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle {v}_{i\alpha }^{(a)}{\dot{r}}_{i\alpha }{{\rm{\Lambda }}}_{i\alpha }\rangle ,$$ (19) denote as local swim stress in the

following, different from the “traditional” swim stress of Eq. (10). Most importantly, the swim stress (10) vanishes in Δ_V_, and, hence, it is not the adequate expression for the

calculation of the local active stress. The vanishing expression (10) in a subvolume lead to the conclusion in ref.27. that the local pressure in an ideal active gas is identical with the

ideal-gas pressure of passive particles when accounting for the respective local density. As a consequence, it was concluded that the active pressure is a boundary effect, because active

forces were not contributing to momentum flux. Our calculations contradict this conclusions. First of all, we find an active flux, Eq. (15), and, secondly, another expression for the local

active stress, Eq. (19). The vanishing average of Eq. (10) in Δ_V_ together with Eq. (12) shows that the contribution by the active momentum is the negative of the active virial, i.e.,

$$\sum _{i=1}^{N}\,\langle {p}_{i\alpha }^{(a)}{r}_{i\alpha }{\dot{{\rm{\Lambda }}}}_{i\alpha }\rangle =-\,\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle {v}_{i\alpha

}^{(a)}{\dot{r}}_{i\alpha }{{\rm{\Lambda }}}_{i\alpha }\rangle .$$ (20) However, if we extend the volume Δ_V_ to the whole volume _V_, i.e., Λ_i_ ≡ 1, Eq. (3) in the Ito formulation yields

\(\langle {v}_{i\alpha }^{(a)}{\dot{r}}_{i\alpha }\rangle ={\gamma }_{R}\langle {v}_{i\alpha }^{(a)}{r}_{i\alpha }\rangle \), and Eqs. (9) and (17) become identical. Note that the wall force

has then to be taken into account in Eq. (17). Thus, our Eq. (19) is a more general expression for the swim stress, since it applies locally as well as globally. GLOBAL STRESS OF IDEAL ABP

GAS For an ideal gas of ABPs, the interparticle forces are zero, i.e., _F__ij_ = 0, and Eq. (9) becomes $$V\,{\sigma }_{\alpha \alpha }^{(i)}=-\,N{k}_{B}T-\sum _{i=1}^{N}\,\gamma \langle

{v}_{i\alpha }^{(a)}{r}_{i\alpha }\rangle -\sum _{i=1}^{N}\,\langle {F}_{i\alpha }^{(w)}({r}_{i\alpha }-{S}_{i\alpha })\rangle ,$$ (21) in the overdamped limit, _m_ = 0. According to

refs24,25, the swim stress (10) can be written as $$\gamma \langle {v}_{i\alpha }^{(a)}{r}_{i\alpha }\rangle =\frac{\gamma }{d{\gamma }_{R}}{v}_{0}^{2}+\frac{1}{{\gamma }_{R}}\langle

{F}_{i\alpha }^{(w)}{v}_{i\alpha }^{(a)}\rangle ,$$ (22) where _d_ is the dimension, which leads to the expression $$V{\sigma }_{\alpha \alpha }^{(i)}=-\,N{k}_{B}T-\frac{\gamma }{3{\gamma

}_{R}}N{v}_{0}^{2}-\frac{1}{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle {F}_{i\alpha }^{(w)}{v}_{i\alpha }^{(a)}\rangle -\sum _{i=1}^{N}\,\langle {F}_{i\alpha }^{(w)}({r}_{i\alpha }-{L}_{\alpha

})\rangle $$ (23) in 3D. The first term on the right-hand side is the thermal contribution to stress, and the second term the ideal gas swim stress22,24,25,44,45 $${\sigma }_{\alpha \alpha

}^{(id)}=-\,\frac{\gamma N}{3{\gamma }_{R}V}{v}_{0}^{2}.$$ (24) Noteworthy, the wall interaction appears twice in Eq. (23). The term proportional to the active velocity reflects and accounts

for wall accumulation, whereas the other term captures finite-range effects of the wall force. LOCAL STRESS OF IDEAL ABP GAS For zero interparticle forces, Eq. (17) becomes $${\rm{\Delta

}}\,V{\sigma }_{\alpha \alpha }^{(i)}=-\,\sum _{i=1}^{N}\,m\langle {\dot{r}}_{i\alpha }^{2}{{\rm{\Lambda }}}_{i\alpha }\rangle -\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{N}\,\langle

{v}_{i\alpha }^{(a)}{\dot{r}}_{i\alpha }{{\rm{\Lambda }}}_{i\alpha }\rangle .$$ (25) With the formal solution of Eq. (1), $${\dot{r}}_{i\alpha }=\frac{1}{m}{\int }_{-\infty

}^{t}\,{e}^{-\gamma (t-t^{\prime} )/m}[\gamma {v}_{i\alpha }^{(a)}(t^{\prime} )+{F}_{i\alpha }(t^{\prime} )+{{\rm{\Gamma }}}_{i\alpha }(t^{\prime} )]dt^{\prime} ,$$ (26) we find $$\langle

{\dot{r}}_{i\alpha }^{2}\rangle =\frac{{k}_{B}T}{m}+\frac{{v}_{0}^{2}}{d\mathrm{(1}+m{\gamma }_{R}/\gamma )},\,\langle {v}_{i\alpha }^{(a)}{\dot{r}}_{i\alpha }\rangle

=\frac{{v}_{0}^{2}}{d\mathrm{(1}+m{\gamma }_{R}/\gamma )}$$ (27) in the stationary state. In the evaluation of these expressions, all wall contributions vanish as long as we assume that the

volume Δ_V_ is located far enough from a wall such that \({e}^{-\gamma (t-{t}_{i}^{(w)})}\ll 1\), where \({t}_{i}^{(w)}\) is the time of the last encounter of an ABP with a wall before

entering Δ_V_. Thus, we obtain $${\rm{\Delta }}\,V{\sigma }_{\alpha \alpha }^{(i)}=-\,{N}_{{\rm{\Delta }}V}({k}_{B}T+\frac{\gamma }{d{\gamma }_{R}}{v}_{0}^{2}),$$ (28) with _N_Δ_V_ the

number of ABPs in the volume Δ_V_. The contributions with the Stokes number _mγ__R_/_γ_ cancel, and the result for the overdamped dynamics is obtained, as already discussed in ref.31.

Evidently, the local stress is independent of the wall force. However, due to wall accumulation, the ABP density is not necessarily homogeneous over the whole volume, in particular, it is

reduced in the bulk. Hence, walls can affect the bulk stress and pressure. For an overdamped and athermal dynamics, Eq. (25) becomes $${\rm{\Delta }}\,V{\sigma }_{\alpha \alpha

}^{(i)}=-\,\frac{\gamma }{{\gamma }_{R}}\sum _{i=1}^{{N}_{\Delta V}}\,\langle {({v}_{i\alpha }^{(a)})}^{2}{{\rm{\Lambda }}}_{i\alpha }\rangle =-\,{N}_{{\rm{\Delta }}V}\frac{\gamma }{3{\gamma

}_{R}}{v}_{0}^{2}$$ (29) in 3D by inserting \({\dot{r}}_{i\alpha }={v}_{i\alpha }^{(a)}\) from Eq. (1), Hence, stress is given by the square of the (active) velocity, similar to the case of

a passive system. Evidently, Eqs (23) and (28) become identical in the limit _L__α_ → ∞, i.e., an infinite volume corresponding to the thermodynamic limit in case of a passive system. Then,

the local particle density _N_Δ_V_/Δ_V_ is equal to the density _N_/_V_, since finite-size effects and the inhomogeneities by surface accumulation become negligible compared to the overall

particle number. However, the equality of the two expressions (23) and (25) applies for all surface separations as long as \(({L}_{\alpha }-{\rm{\Delta }}{L}_{\alpha })/{l}_{p}\gg 1\), where

_l__p_ = _v_0/_γ__R_ is the persistence length of the active motion. The surface forces in Eq. (23) yield additional contributions to the ideal active gas stress. Associated bulk-density

variations change the respective values of the local stress (28). Figure 2 shows simulation results for the local swim stress of non-interacting ABPs in the subvolume Δ_V_ according to Eq.

(19) as function of the center position _r__z_ of Δ_V_, where _L_z = 100_σ_ and Δ_L__z_ = 0.05_L__z_. Activity is characterized by the Péclet number _Pe_ = _v_0/_σD__R_, where _Pe_ = 20 in

Fig. 2. In addition, the global wall stress according to Eq. (21) (_k__B__T_ = 0) is presented. Evidently, the local stress is independent of the location of the subvolume Δ_V_ in the bulk

of the system and it agrees with the wall stress within 1%. Our results indicate that stress in an active system is not a wall effect. According to Eq. (29), the local stress is proportional

to the square of the active velocity of the ABPs within Δ_V_, similar to the dependence on the kinetic energy in passive systems. Moreover, the simulations confirm the presence of an active

momentum flux with the momentum of Eq. (15). The dependence of the stress on the activity is presented in Fig. 3(a). The local swim stress (19) coincides perfectly with the wall stress (23)

(_k__B__T_ = 0) of the system. The scaled stress $$\frac{{\sigma }_{zz}^{(i)}{\sigma }^{2}}{\gamma {v}_{0}}=-\,\frac{{\rho }_{{\rm{\Delta }}V}{\sigma }^{3}}{6}Pe,$$ (30) where _ρ_Δ_V_ = 

_N_Δ_V_/Δ_V_ is the bulk density, decreases monotonically with increasing Péclet number, but deviates from the linear dependence of an unconfined (periodic boundary conditions) ideal ABP gas

for large _Pe_27,46,47. The stress reduction is a consequence of an enhanced ABP surface accumulation with increasing _Pe_ and, correspondingly, a reduction of the bulk density. Here, we

like to emphasize that the stresses calculated via Eqs (8) and (9) perfectly agree with each other. Figure 3(b) shows the relative density difference Δ_ρ_/_ρ_ = (_ρ_ − _ρ_Δ_V_)/_ρ_ with

respect to the mean density _ρ_ = _N_/_V_ as function of the Péclet number (squares). The simulation data, with the bulk density _ρ_Δ_V_, can well be described by the relation

$$\frac{{\rm{\Delta }}\rho }{\rho }=\frac{1}{1+0.7{L}_{z}/{l}_{p}},$$ (31) which approaches zero in the limits _L__z_ → ∞ and _Pe_ → 0, and the bulk density becomes equal to the average

density _ρ_ as for an passive ideal gas. Such a dependence on _L__z_/_l__p_ has been obtained in ref.27. for the fraction of adsorbed ABPs at a wall. However, the numerical factor is

somewhat different, we find 0.7 compared to 0.6 in ref.27. The difference could be related to the different adopted dimensionalities, _d_ = 3 here versus _d_ = 2 in ref.27. Moreover, Fig. 

3(b) shows that the wall virial \({\sum }_{i}\,\langle {F}_{i\alpha }^{(w)}{v}_{i\alpha }^{(a)}\rangle /{\gamma }_{R}\) (23) divided by the ideal ABP swim stress (24) is identical with the

relative density difference Δ_ρ_/_ρ_ and, thus, exhibits the same dependence on the Péclet number (the finite-range wall-force contribution is negligible). Of course, this is expected by the

equivalence of the stress expressions (21) and (25). Figure 4 illustrates the dependence of the stress on the wall separation _L__z_ for the Péclet number _Pe_ = 40. Again, simulation

results for wall and local stress agree very well. With increasing system size, the wall effect decreases and the stress approaches the value of the ideal bulk stress. The relation between

the local density and the system size is displayed in the inset of Fig. 4, which is well described by Eq. (31). The dependence of the ideal active gas stress on the Péclet number and system

size is solely described by the respective dependence of the density _ρ_Δ_V_ on these quantities, since \({\sigma }_{zz}^{(i)}={\sigma }_{zz}^{(id)}{\rho }_{{\rm{\Delta }}V}/\rho \). This is

confirmed in Figs 3(a) and 4. Some of our findings seem to be rather evident as soon as the validity of the Eq. (29) is taken for granted. However, this expression follows from our local

stress with the local swim stress (19), and not the stress expression for the system with walls. Specifically, ref.27 discusses wall-induced effects only. Hence, by our studies we emphasize

the existence of a bulk stress and pressure and its identity with the respective wall values. INTERACTING ABPS Simulation results for the local interparticle force (18), local active (19),

and global stress of ABP systems with excluded-volume interactions are depicted in Fig. 5(a) as function of the packing fraction _ϕ_. Again, we obtain excellent agreement between the various

stress-tensor contributions calculated both, globally and locally. Consistent with previous studies, the magnitude of the swim stress contribution decreases with increasing density, whereas

the magnitude of the interparticle force contribution monotonically increases over the considered concentration range16,25,48. Above _ϕ_ ≈ 0.4, the contribution due to interparticle forces

dominates the overall stress. Figure 5(b) compares the local swim and interparticle stresses with those in the overall system for various wall distances and concentrations. Remarkably, the

local swim stress (bullets) is independent of the wall separation, except for _ϕ_ = 0.25. In this case, the volume Δ_V_ is not sufficiently far away from the walls, and due to the comparably

large persistence length _l__p_ = 5_σ_, the ABP velocity is affected by wall interactions (cf. Eq. (26)). The effect vanishes with increasing concentration, since the persistence length

decreases due to enhanced particle collisions at higher concentrations. The local swim stress in Δ_V_ (19) can be separated into two contributions by inserting the athermal and overdamped

equation of motion (Eq. (1)), namely $${\sigma }_{\alpha \alpha }^{(s)}={\sigma }_{\alpha \alpha }^{(id)}-\frac{1}{{\gamma }_{R}}\sum _{i=1}^{N}\,\underset{j=1}{\overset{N}{\sum ^{\prime}

}}{F}_{ij\alpha }{v}_{i\alpha }^{(a)}{{\rm{\Lambda }}}_{i\alpha }.$$ (32) Hence, the reduction of the relative local swim stress in Fig. 5(a) is a consequence of the correlations between the

interparticle forces and the propulsion direction. The effect increases with increasing concentration. We like to emphasize that density variations in the bulk are negligible small for the

considered wall separations in Fig. 5(b). In fact, surface accumulation is lower in a system of self-avoiding ABPs compared to an ideal ABP gas. The global swim stress (10) includes, in

addition to the terms in Eq. (32), a wall contribution as shown in ref.25. It is the latter part, which implies a system-size dependence of the global swim stress (open circles in Fig. 

5(b)). The effect gradually vanishes with increasing system size. In contrast, the global interparticle-force stress is independent of system size, which can be expected for a system at

constant average density _ρ_. However, the local interparticle-force stress depends on _L__z_. Since the total local and global stresses are equal, the system-size dependence of the local

interparticle-force stress and that of the global swim stress are equal. Figure 5(b) clearly reveals differences between the global swim (Eq. (9)) and local swim stress (Eq. (17)),

specifically for finite system sizes. However, in the thermodynamic limit of infinitely large systems, the two definitions yield identical results. The total stress in a volume _V_ (global)

or Δ_V_ (local) is not affected by the difference, since other contributions by interparticle forces yield identical differences and, hence, compensate for the disparity in the swim

stresses. LOCAL STRESS IN INHOMOGENEOUS SYSTEMS OF ABPS The stress in phase-separated, inhomogeneous ABP systems has been calculated before by various methods49,50. The calculation of the

global stress in ref.49 is performed with a particle-based model (ABPs) in a system with periodic boundary conditions. However, no stress normal to the interface has been obtained. In

ref.50, a continuum description based on a generalization of the Cahn-Hilliard equation is applied. Here, we illustrate the suitability of our particle-based expression for the calculation

of local stresses for a phase-separated system of ABPs confined between two walls. The same geometry is considered as before, but with the dimensions _L__x_ = _L__y_ = 25_σ_. The Péclet

number _Pe_ = 80 is sufficiently large to yield phase separation into crystalline-like layers adjacent to walls and a fluid phase in the center, as is displayed in Fig. 6(a,b). In order to

calculate the local stress, we consider local volumes of width Δ_L__z_ = 4_σ_, i.e., we average over four crystalline layers. As shown in Fig. 6(c), the stress normal to the walls and the

interface (_z_ direction) is constant over the whole system. Moreover, the local stress agrees with the stress exerted on the wall. In the various regimes, stress is dominated either by the

swim stress (Eq. (19)) (central fluid part) or the force contribution to stress (Eq. (18)) (crystalline wall part). Specifically in the crossover regime, where both stresses contribute, the

local stress is equal to the global stress (wall stress). This result confirms that the derived expression is suitable for calculating local stress even in inhomogeneous systems. SUMMARY AND

CONCLUSIONS We have derived expressions for the stress (pressure) of a system of confined active Brownian particles, specifically, generally valid expressions for the local stress in a

subvolume Δ_V_(_R_) centered around a point _R_. In addition to previously derived contributions to the stress of active systems confined between walls25, the contribution of the

finite-range surface interaction is taken into account in the calculation of the global stress. For the stress in a local volume (Δ_V_), we find two expressions by following the strategy of

ref.37. On the one hand, stress is given by momentum transfer across a hypothetical plane, including force as well as kinetic (momentum) contributions. Here, we find a motility contribution

by introducing an active momentum in analogy to the kinetic momentum of a particle of mass _m_. On the other hand, we identify a virial expression for the active stress (local swim stress)

of particles inside of Δ_V_, different from the known swim stress22,25,42. In fact, in ref.36 a formally similar expression has been defined, however, with an active impulse of very

different meaning. Computer simulations show that our obtained local stress expression agrees quantitatively with the corresponding global stress expression of an ABP system confined between

walls for both, non-interacting ABPs as well as ABPs interacting via a Lennard-Jones potential. This underlines the existence of an equation of state for a system of spherical ABPs. Our

results reach beyond previous considerations and discussions on the stress in active systems. Initially, swim pressure has been introduce via Clausius’ virial51, taking active forces into

account22,23. Based on the equations of motion of ABPs for an infinite system, the swim pressure of an ideal active gas has then been proposed22. Subsequently, derivations of active pressure

expressions have been presented for ABPs confined between walls25,26,27 or in periodic systems25,27. Alternatively, pressure expressions have been determined via the Fokker-Planck equation

of an ABP system28, or the equations of motion for the density field36. A derivation of an expression for a local pressure has be attempted in ref.27, with the conclusion that a local

pressures exists, but the bulk value differs from the mechanical pressure exerted on confining walls. In case of an ideal gas of ABPs, the bulk pressure would be given by _ρ_(_R_)_k__B__T_,

with the position dependent density _ρ_(_R_) and, hence, would vanish in an athermal system. Hence, active pressure is considered as a boundary effect27. In contrast, the present

calculations provide a general expression for the local stress and pressure and thus, mark a substantial advancement. The derived local stress/pressure expressions are more general and

reduce to the known expressions in the limit of the local volume being equal to the overall volume. This is emphasized by the fact that the local swim stress (19) is finite, while the

“traditional” swim stress (10) vanishes in Δ_V_. Most importantly, our calculations demonstrated that active stress/pressure is not a wall (boundary) effect, as stated in ref.27, but is

caused by active momentum transport in analogy to momentum transfer in a passive system. Hence, our results allow us to resolve apparent contradictions in the interpretation of local stress

and consequently in the existence of equations of state in active systems. As we demonstrated, local stress or pressure can be calculated in inhomogeneous ABP systems. Extensions to local

shear stresses are straightforward and, thus, surface tensions of active systems can be determined. METHODS We perform simulations in three dimensions considering the overdamped Eq. (1), _m_

 = 0, without thermal fluctuations. The translational equations of motion (1) are solved via the Ermak-McCammon algorithm52. The equations of motion (3) for the orientation vectors are

solved using the scheme described in ref.25. Pair-wise interparticle interactions are taken into account by the repulsive Lennard-Jones potential $${U}_{LJ}=\{\begin{array}{cc}\varepsilon

[{(\frac{\sigma }{{r}_{ij}})}^{12}-{(\frac{\sigma }{{r}_{ij}})}^{6}+\frac{1}{4}], & {r}_{ij}\le \sqrt[6]{2}\sigma \\ \mathrm{0,} & {r}_{ij} > \sqrt[6]{2}\sigma \end{array},$$ (33)

where _r__ij_ = |_R__ij_| and the interaction strength is set to _ε_/_k__B__T_ = _Pe_; _Pe_ is the Péclet number defined as $$Pe=\frac{{v}_{0}}{\sigma {D}_{R}}.$$ (34) This yields the same

particle overlap independent of the Péclet number53. The ABPs are confined between two walls parallel to the _xy_-plane of the Cartesian reference frame located at _S__iz_ = ±_L__z_/2 (cf.

Fig. 1). Parallel to the walls, periodic boundary conditions are applied. The purely repulsive ABP-wall interaction is described by the Lennard-Jones potential of Eq. (33) with _r__ij_

replaced by _z__i_ − _S__iz_. We determine the stress _σ__zz_ along the _z_-axis in two ways. Firstly, we calculate the global stress of the whole system according to Eq. (9) (_m_ = 0).

Secondly, the local stress in a volume Δ_V_ is calculated via Eq. (17). Thereby, the box dimension _L__z_ normal to the walls is chosen such that it is significantly larger than the

persistence length _l__p_ = _v_0/2_D__R_ = _Peσ_/2 of an ABP, in particular, we consider wall separations \({L}_{z}\geqslant 5{l}_{p}\). The volume Δ_V_ of width Δ_L__z_ is located in the

bulk of the system along the _z_-axis (cf. Fig. 1). If not indicated otherwise, the dimensions of the volume _V_ are _L__x_ = _L__y_ = 40_σ_, _L__z_ = 100_σ_, and Δ_L__z_ = 0.2_L__z_. In

Fig. 1, _r__z_ denotes the position of the center of the slit within the interval _L__z_/2 < _r__z_ < _L__z_/2. The number density of ABPs in _V_ is _ρσ_3 = 0.3. We perform at least

three independent simulations runs of 2 × 107 time steps each, with the time step _dt_ = 10−3_σ_/_v_0. Thus, every presented data point is averaged over approximately 103 independent

configurations. REFERENCES * Ramaswamy, S. The mechanics and statistics of active matter. _Annu. Rev. Cond. Mat. Phys._ 1, 323, https://doi.org/10.1146/annurev-conmatphys-070909-104101

(2010). Article  ADS  Google Scholar  * Cates, M. E. & MacKintosh, F. C. Active soft matter. _Soft Matter_ 7, 3050, https://doi.org/10.1039/C1SM90014E (2011). Article  ADS  CAS  Google

Scholar  * Marchetti, M. C. _et al_. Hydrodynamics of soft active matter. _Rev. Mod. Phys._ 85, 1143, https://doi.org/10.1103/RevModPhys.85.1143 (2013). Article  ADS  CAS  Google Scholar  *

Elgeti, J., Winkler, R. G. & Gompper, G. Physics of microswimmers-single particle motion and collective behavior: a review. _Rep. Prog. Phys._ 78, 056601,

https://doi.org/10.1088/0034-4885/78/5/056601 (2015). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Bechinger, C. _et al_. Active particles in complex and crowded environments.

_Rev. Mod. Phys._ 88, 045006, https://doi.org/10.1103/RevModPhys.88.045006 (2016). Article  ADS  MathSciNet  Google Scholar  * Fily, Y. & Marchetti, M. C. Athermal phase separation of

self-propelled particles with no alignment. _Phys. Rev. Lett._ 108, 235702, https://doi.org/10.1103/PhysRevLett.108.235702 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Theurkauff,

I., Cottin-Bizonne, C., Palacci, J., Ybert, C. & Bocquet, L. Dynamic clustering in active colloidal suspensions with chemical signaling. _Phys. Rev. Lett._ 108, 268303,

https://doi.org/10.1103/PhysRevLett.108.268303 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Buttinoni, I. _et al_. Dynamical clustering and phase separation in suspensions of

self-propelled colloidal particles. _Phys. Rev. Lett._ 110, 238301, https://doi.org/10.1103/PhysRevLett.110.238301 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Redner, G. S., Hagan,

M. F. & Baskaran, A. Structure and dynamics of a phase-separating active colloidal fluid. _Phys. Rev. Lett._ 110, 055701, https://doi.org/10.1103/PhysRevLett.110.055701 (2013). Article 

ADS  CAS  PubMed  Google Scholar  * Bialké, J., Speck, T. & Löwen, H. Crystallization in a dense suspension of self-propelled particles. _Phys. Rev. Lett._ 108, 168301,

https://doi.org/10.1103/PhysRevLett.108.168301 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Wittkowski, R. _et al_. Scalar _ϕ_ 4 field theory for active-particle phase separation

field theory for active-particle phase separation. _Nat. Commun._ 5, 4351 (2014). Article  CAS  Google Scholar  * Cates, M. E. & Tailleur, J. Motility-induced phase separation. _Annu.

Rev. Condens. Matter Phys._ 6, 219, https://doi.org/10.1146/annurev-conmatphys-031214-014710 (2015). Article  ADS  CAS  Google Scholar  * Wysocki, A., Winkler, R. G. & Gompper, G.

Cooperative motion of active Brownian spheres in three-dimensional dense suspensions. _EPL_ 105, 48004, https://doi.org/10.1209/0295-5075/105/48004 (2014). Article  ADS  CAS  Google Scholar

  * Stenhammar, J., Marenduzzo, D., Allen, R. J. & Cates, M. E. Phase behaviour of active Brownian particles: the role of dimensionality. _Soft Matter_ 10, 1489,

https://doi.org/10.1039/C3SM52813H (2014). Article  ADS  CAS  PubMed  Google Scholar  * Wysocki, A., Winkler, R. G. & Gompper, G. Propagating interfaces in mixtures of active and passive

Brownian particles. _New J. Phys._ 18, 123030, https://doi.org/10.1088/1367-2630/aa529d (2016). Article  ADS  Google Scholar  * Marchetti, M. C., Fily, Y., Henkes, S., Patch, A. &

Yllanes, D. Minimal model of active colloids highlights the role of mechanical interactions in controlling the emergent behavior of active matter. _Curr. Opin. Colloid Interface Sci._ 21,

34, https://doi.org/10.1016/j.cocis.2016.01.003 (2016). Article  CAS  Google Scholar  * Theers, M., Westphal, E., Qi, K., Winkler, R. G. & Gompper, G. Clustering of microswimmers:

interplay of shape and hydrodynamics. _Soft Matter_ 14, 8590, https://doi.org/10.1039/C8SM01390J (2018). Article  ADS  CAS  PubMed  Google Scholar  * Berke, A. P., Turner, L., Berg, H. C.

& Lauga, E. Hydrodynamic attraction of swimming microorganisms by surfaces. _Phys. Rev. Lett._ 101, 038102, https://doi.org/10.1103/PhysRevLett.101.038102 (2008). Article  ADS  CAS 

PubMed  Google Scholar  * Lee, C. F. Active particles under confinement: aggregation at the wall and gradient formation inside a channel. _New J. Phys._ 15, 055007,

https://doi.org/10.1088/1367-2630/15/5/055007 (2013). Article  ADS  MathSciNet  Google Scholar  * Elgeti, J. & Gompper, G. Wall accumulation of self-propelled spheres. _EPL_ 101, 48003

(2013). Article  ADS  CAS  Google Scholar  * Fily, Y., Baskaran, A. & Hagan, M. F. Dynamics of self-propelled particles under strong confinement. _Soft Matter_ 10, 5609,

https://doi.org/10.1039/C4SM00975D (2014). Article  ADS  CAS  PubMed  Google Scholar  * Takatori, S. C., Yan, W. & Brady, J. F. Swim pressure: Stress generation in active matter. _Phys.

Rev. Lett._ 113, 028103, https://doi.org/10.1103/PhysRevLett.113.028103 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Yang, X., Manning, M. L. & Marchetti, M. C. Aggregation and

segregation of confined active particles. _Soft Matter_ 10, 6477, https://doi.org/10.1039/C4SM00927D (2014). Article  ADS  CAS  PubMed  Google Scholar  * Solon, A. P. _et al_. Pressure and

phase equilibria in interacting active Brownian spheres. _Phys. Rev. Lett._ 114, 198301, https://doi.org/10.1103/PhysRevLett.114.198301 (2015). Article  ADS  CAS  PubMed  Google Scholar  *

Winkler, R. G., Wysocki, A. & Gompper, G. Virial pressure in systems of spherical active Brownian particles. _Soft Matter_ 11, 6680, https://doi.org/10.1039/C5SM01412C (2015). Article 

ADS  CAS  PubMed  Google Scholar  * Falasco, G., Baldovin, F., Kroy, K. & Baiesi, M. Mesoscopic virial equation for nonequilibrium statistical mechanics. _New J. Phys._ 18, 093043,

https://doi.org/10.1088/1367-2630/18/9/093043 (2016). Article  ADS  Google Scholar  * Speck, T. & Jack, R. L. Ideal bulk pressure of active Brownian particles. _Phys. Rev. E_ 93, 062605,

https://doi.org/10.1103/PhysRevE.93.062605 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Solon, A. P. _et al_. Pressure is not a state function for generic active fluids. _Nat.

Phys._ 11, 673, https://doi.org/10.1038/nphys3377 (2015). Article  CAS  Google Scholar  * Steffenoni, S., Falasco, G. & Kroy, K. Microscopic derivation of the hydrodynamics of

active-Brownian-particle suspensions. _Phys. Rev. E_ 95, 052142, https://doi.org/10.1103/PhysRevE.95.052142 (2017). Article  ADS  PubMed  Google Scholar  * Joyeux, M. & Bertin, E.

Pressure of a gas of underdamped active dumbbells. _Phys. Rev. E_ 93, 032605, https://doi.org/10.1103/PhysRevE.93.032605 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Takatori, S. C.

& Brady, J. F. Inertial effects on the stress generation of active fluids. _Phys. Rev. Fluid_ 2, 094305, https://doi.org/10.1103/PhysRevFluids.2.094305 (2017). Article  ADS  Google

Scholar  * Ginot, F. _et al_. Nonequilibrium equation of state in suspensions of active colloids. _Phys. Rev. X_ 5, 011004, https://doi.org/10.1103/PhysRevX.5.011004 (2015). Article  CAS 

Google Scholar  * Bertin, E. An equation of state for active matter. _Phys._ 8, 44, https://doi.org/10.1103/Physics.8.44 (2015). Article  Google Scholar  * Nikola, N. _et al_. Active

particles with soft and curved walls: Equation of state, ratchets, and instabilities. _Phys. Rev. Lett._ 117, 098001, https://doi.org/10.1103/PhysRevLett.117.098001 (2016). Article  ADS  CAS

  PubMed  Google Scholar  * Junot, G., Briand, G., Ledesma-Alonso, R. & Dauchot, O. Active versus passive hard disks against a membrane: Mechanical pressure and instability. _Phys. Rev.

Lett._ 119, 028002, https://doi.org/10.1103/PhysRevLett.119.028002 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Fily, Y., Kafri, Y., Solon, A. P., Tailleur, J. & Turner, A.

Mechanical pressure and momentum conservation in dry active matter. _J. Phys. A: Math. Theor._ 51, 044003, https://doi.org/10.1088/1751-8121/aa99b6 (2018). Article  ADS  MathSciNet  MATH 

Google Scholar  * Lion, T. W. & Allen, R. J. Computing the local pressure in molecular dynamics simulations. _J. Phys.: Condens. Matter_ 24, 284133,

https://doi.org/10.1088/0953-8984/24/28/284133 (2012). Article  CAS  Google Scholar  * Raible, M. & Engel, A. Langevin equation for the rotation of a magnetic particle. _Appl.

Organometal. Chem._ 18, 536, https://doi.org/10.1002/aoc.757 (2004). Article  CAS  Google Scholar  * Das, S., Gompper, G. & Winkler, R. G. Confined active Brownian particles: theoretical

description of propulsion-induced accumulation. _New J. Phys._ 20, 015001, https://doi.org/10.1088/1367-2630/aa9d4b (2018). Article  ADS  Google Scholar  * Fodor, É. _et al_. How far from

equilibrium is active matter? _Phys. Rev. Lett._ 117, 038103, https://doi.org/10.1103/PhysRevLett.117.038103 (2016). Article  ADS  MathSciNet  CAS  PubMed  Google Scholar  * Winkler, R. G.

& Hentschke, R. Liquid benzene confined between graphite surfaces. a constant pressure molecular dynamics study. _J. Chem. Phys._ 99, 5405 (1993). Article  ADS  CAS  Google Scholar  *

Takatori, S. C. & Brady, J. F. Swim stress, motion, and deformation of active matter: effect of an external field. _Soft Matter_ 10, 9433, https://doi.org/10.1039/C4SM01409J (2014).

Article  ADS  CAS  PubMed  Google Scholar  * Risken, H. _The Fokker-Planck Equation_. (Springer, Berlin, 1989). * Mallory, S. A., Šarić, A., Valeriani, C. & Cacciuto, A. Anomalous

thermomechanical properties of a self-propelled colloidal fluid. _Phys. Rev. E_ 89, 052303, https://doi.org/10.1103/PhysRevE.89.052303 (2014). Article  ADS  CAS  Google Scholar  *

Smallenburg, F. & Löwen, H. Swim pressure on walls with curves and corners. _Phys. Rev. E_ 92, 032304, https://doi.org/10.1103/PhysRevE.92.032304 (2015). Article  ADS  CAS  Google

Scholar  * Yan, W. & Brady, J. F. The force on a boundary in active matter. _J. Fluid Mech._ 785, R1, https://doi.org/10.1017/jfm.2015.621 (2015). Article  ADS  MathSciNet  MATH  Google

Scholar  * Ezhilan, B., Alonso-Matilla, R. & Saintillan, D. On the distribution and swim pressure of run-and-tumble particles in confinement. _J. Fluid Mech._ 781, R4,

https://doi.org/10.1017/jfm.2015.520 (2015). Article  ADS  MathSciNet  MATH  Google Scholar  * Takatori, S. C. & Brady, J. F. Forces, stresses and the (thermo?) dynamics of active

matter. _Curr. Opin. Colloid Interface Sci._ 21, 24, https://doi.org/10.1016/j.cocis.2015.12.003 (2016). Article  CAS  Google Scholar  * Bialké, J., Siebert, J. T., Löwen, H. & Speck, T.

Negative interfacial tension in phase-separated active Brownian particles. _Phys. Rev. Lett._ 115, 098301, https://doi.org/10.1103/PhysRevLett.115.098301 (2015). Article  ADS  CAS  PubMed 

Google Scholar  * Solon, A. P., Stenhammar, J., Cates, M. E., Kafri, Y. & Tailleur, J. Generalized thermodynamics of phase equilibria in scalar active matter. _Phys. Rev. E_ 97, 020602,

https://doi.org/10.1103/PhysRevE.97.020602 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Becker, R. _Theory of Heat_. (Springer Verlag, Berlin, 1967). * Ermak, D. L. & McCammon,

J. Brownian dynamics with hydrodynamic interactions. _J. Chem. Phys._ 69, 1352, https://doi.org/10.1063/1.436761 (1978). Article  ADS  CAS  Google Scholar  * Fily, Y., Henkes, S. &

Marchetti, M. C. Freezing and phase separation of self-propelled disks. _Soft Matter_ 10, 2132, https://doi.org/10.1039/C3SM52469H (2014). Article  ADS  CAS  PubMed  Google Scholar  Download

references ACKNOWLEDGEMENTS Financial support by the Deutsche Forschungsgemeinschaft (DFG) within the priority program SPP 1726 “Microswimmers—from Single Particle Motion to Collective

Behaviour” is gratefully acknowledged. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Theoretical Soft Matter and Biophysics, Institute of Complex Systems and Institute for Advanced

Simulation, Forschungszentrum Jülich, 52425, Jülich, Germany Shibananda Das, Gerhard Gompper & Roland G. Winkler Authors * Shibananda Das View author publications You can also search for

this author inPubMed Google Scholar * Gerhard Gompper View author publications You can also search for this author inPubMed Google Scholar * Roland G. Winkler View author publications You

can also search for this author inPubMed Google Scholar CONTRIBUTIONS R.G.W. and G.G. conceived the project. R.G.W. and S.D. performed the analytical calculations. S.D. designed the

simulation algorithm and performed the simulations. R.G.W., S.D., and G.G. interpreted the data and wrote the paper. All authors discussed the results and commented on the manuscript.

CORRESPONDING AUTHOR Correspondence to Roland G. Winkler. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE:

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a

Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit

to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are

included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and

your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this

license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Das, S., Gompper, G. & Winkler, R.G. Local stress and pressure

in an inhomogeneous system of spherical active Brownian particles. _Sci Rep_ 9, 6608 (2019). https://doi.org/10.1038/s41598-019-43077-x Download citation * Received: 22 August 2018 *

Accepted: 15 April 2019 * Published: 29 April 2019 * DOI: https://doi.org/10.1038/s41598-019-43077-x SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative