Reader TTS

ABSTRACT In recent cross-disciplinary studies involving both optics and computing, single-photon-based decision-making has been demonstrated by utilizing the wave-particle duality of light

to solve multi-armed bandit problems. Furthermore, entangled-photon-based decision-making has managed to solve a competitive multi-armed bandit problem in such a way that conflicts of

decisions among players are avoided while ensuring equality. However, as these studies are based on the polarization of light, the number of available choices is limited to two,

corresponding to two orthogonal polarization states. Here we propose a scalable principle to solve competitive decision-making situations by using the orbital angular momentum of photons

based on its high dimensionality, which theoretically allows an unlimited number of arms. Moreover, by extending the Hong-Ou-Mandel effect to more than two states, we theoretically establish

an experimental configuration able to generate multi-photon states with orbital angular momentum and conditions that provide conflict-free selections at every turn. We numerically examine

total rewards regarding three-armed bandit problems, for which the proposed strategy accomplishes almost the theoretical maximum, which is greater than a conventional mixed strategy

intending to realize Nash equilibrium. This is thanks to the quantum interference effect that achieves no-conflict selections, even in the exploring phase to find the best arms. SIMILAR

CONTENT BEING VIEWED BY OTHERS ENTANGLED _N_-PHOTON STATES FOR FAIR AND OPTIMAL SOCIAL DECISION MAKING Article Open access 24 November 2020 ENTANGLED AND CORRELATED PHOTON MIXED STRATEGY FOR

SOCIAL DECISION MAKING Article Open access 01 March 2021 ASYMMETRIC QUANTUM DECISION-MAKING Article Open access 05 September 2023 INTRODUCTION Optics and photonics are expected to play

crucial roles in future computing systems1, making a variety of devices and systems to be intensively studied such as optical fibre-based neuromorphic computing2, on-chip optical neural

networks3, optical reservoir computing4, among others. While these works are basically categorized in supervised learning, reinforcement learning is another important branch of artificial

intelligence5. The Multi-Armed Bandit (MAB) problem is an example of a reinforcement learning situation, which formulates a fundamental issue of decision making in dynamically changing

uncertain environments where the target is to find the best selection among many slot machines, also referred to as arms, whose reward probabilities are unknown6. In solving MAB problems,

exploration actions are necessary to find the best arm, although too much exploration may reduce the final amount of obtained reward from the exploitation. On the opposite, insufficient

exploration may lead to miss the best arm. Furthermore, when multiple players are involved, decision conflicts become serious, as they induce congestions and inhibit socially achievable

benefits7,8. Equality among players is another critical issue, as unfair repartition of outcomes may lead to distrust the system. This whole problem is known as the competitive MAB (CMAB)

problem. In order to solve these complex issues, photonic solutions have been recently considered. For example, the wave-particle duality of single photons has been utilized for the

resolution of the two-armed bandit problem9. Moreover, Chauvet et al. theoretically and experimentally demonstrated that polarization entangled photon pairs provide non-conflict and

equality-assured decisions in two-player, two-armed bandit problems10. Entangled photon states that allow more than three players while guaranteeing optimal outcome and equal repartition

have also been demonstrated11. However, since these former principles rely on the polarization of light as the tunable degree of freedom, the number of possible selections or arms is limited

to only two, although potential scalability for the single-player MAB is feasible within a tournament-based approach12. Therefore, the scalable principle of decision-making has been an

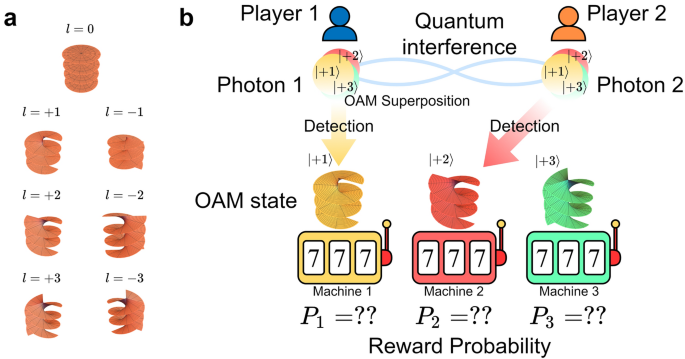
important and fundamental issue, especially for multiplayer situations. In this paper, we introduce the use of the orbital angular momentum (OAM) of photons13,14 to resolve the scalability

issue of photonic decision making, following the concept summarized in Fig. 1. Photons that carry OAM13 realize high-dimensional state spaces, only restricted by the precision and accuracy

of the generation technique and the transmission medium15 (Fig. 1a); hence one of the basic ideas of this study is to associate individual selections to different-valued OAM (Fig. 1b). The

applications of OAM have progressed in diverse areas ranging from the manipulation of cooled atoms, communications, nonlinear optics, optical solitons, and so on. The high-dimensionality of

OAM is particularly attractive for quantum information processing in increasing the dimension of elementary quantum information carriers to go beyond the qubit16,17,18,19,20,21. Likewise, in

the present study, the multi-dimensionality of OAM plays a crucial role in extending the maximum number of arms as well as utilizing the probabilistic attribute of single photons carrying

OAM. Furthermore, to resolve CMAB problems when the number of arms is greater than two, we extend the notion of Hong-Ou-Mandel effect22 to more than two (OAM) vector states to induce quantum

interference. We show that conflicting decisions among two players can be perfectly avoided by the adequate quantum interference design to generate OAM 2-photon states, relying on a

coherent photon pair source. In the literature, OAM has been examined from game-theoretic perspectives such as resolving prisoners dilemma23 and duel game24. In the present study, we benefit

from quantum interference for non-conflicting decision-making to maximize total rewards, which is similar to the insight gained by quantum game literature. Additionally, in solving CMAB

problems with many arms, exploration action is necessary. We numerically examine total rewards regarding three-armed bandit problems where the proposed quantum-interference-based strategy

accomplishes nearly theoretical maximum total reward. We confirm that the proposed strategy clearly outperforms conventional ones, including the mixed strategy intending to realize Nash

equilibrium7. Moreover, equality among players is important in CMAB problems. We demonstrate that equality is perfectly ensured by appropriate quantum interference constructions when the

number of arms is three. At the same time, however, we also show that it is unfortunately impossible to accomplish perfect equality in the proposed scheme and with the current hypotheses

when the number of arms is equal to or larger than four. Note also that perfect collision avoidance is ensured for any number of arms. These properties are made possible thanks to the high

dimensionalities of OAM for scalability and the quantum interference effect for non-conflict selections even in the exploring phase to find the best arms. RESULTS SCALABLE DECISION MAKER

WITH OAM SYSTEM ARCHITECTURE FOR SOLVING 1-PLAYER K-ARMED BANDIT PROBLEM We first describe the problem under study, which is a stochastic multi-armed bandit problem with rewards following

Bernoulli distributions defined as follows. There are _K_ available slot machines (or arms): when the player selects one arm _i_, the player wins with probability \(P_i\) (and receives a

fixed reward of 1), or loses with probability \(1-P_{i}\) (and receives a fixed reward of 0), with _i_ an integer ranging from 1 to _K_. Let a player choose an arm each time and allow a

total of _T_ times, then the goal of the bandit problem is to find out which strategy should be followed to choose arms so that the resultant accumulated outcome is maximized. When the slot

machine with the highest winning probability is known, the best strategy is to draw that specific arm for all _T_ times, but the player initially has no information about the arms.

Therefore, exploration actions are required to know the best arm, whereas too much exploration potentially leads to missing a higher total amount of rewards from the best machine. In the

previous work on single-photon decision maker using polarization9, two orthogonal linear polarizations of photons are associated with two slot machines; that is, horizontal and vertical

polarizations correspond to slot machine 1 and 2, respectively. The exploration is physically realized by the probabilistic attribute of photon measurement, whose outcome depends on the

direction of the polarization of linearly polarized single photons. Therein, the polarization degree of freedom physically and directly allows specifying the probabilistic selection of slot

machines. However, as mentioned in the “Introduction” section, the number of arms is limited to only two, although extendable in a single-player setup to powers of two via a tournament-based

approach12. The fundamental idea of the present study is to associate the dimension of OAM with the selection of multiple arms, whatever the number of arms. Allen et al. have pointed out

that a Laguerre-Gaussian (LG) beam has an angular momentum independent from polarization; they have called it OAM to distinguish it from the polarization-dependent spin angular momentum25.

The spatial mode of a LG beam can be expressed using the near-axis approximation $$\begin{aligned} \begin{aligned} u_l = f_m(\rho ,z)e^{i l\theta }e^{i k z} \end{aligned} \end{aligned}$$ (1)

where \(\rho \) is the distance from the optical axis, \(\theta \) is the azimuthal angle around the optical axis, _z_ is the coordinate of the propagation direction, \(f_m\) is the complex

amplitude distribution, and _k_ is the wavenumber. _m_ and _l_ are integer numbers that respectively describe the order of the Laguerre polynomial for the radial distribution and the

azimuthal rotation number. In our study, _m_ is fixed at 0, while _l_ takes any integer numbers. Correspondingly, \({|{l}\rangle }\) is the state in which there is one photon in the _l_

mode, whose angular momentum is equal to \(l \hbar \) where \(\hbar \) is Planck’s constant divided by \(2\pi \). Since the modes with different _l_ are orthogonal to each other, the quantum

state can be expressed by a linear superposition, using these modes as a basis. Figure 1a schematically illustrates examples of beams with different _l_-valued OAM where _l_ is an integer

from \(-3\) to 3. Non-zero _l_ beams exhibit spiral isophase spatial distributions. Figure 2 shows a schematic diagram of the proposed system architecture for solving the MAB problem using

OAM. Here we illustrate the case where the number of arms is three, but the same principle applies in extending to a larger number of arms. Conventional laser sources generate beams that do

not have orbital angular momentum. Technologically, methods to generate light with OAM from a plane wave or a Gaussian beam include the use of phase plates26, computer generated holograms

(CGH)27, or mode converters28,29. Spatial light modulators (SLMs) are widely utilized for this purpose, as they enable direct and tunable amplitude and/or phase modulation of an incoming

light beam30. The simplest and the most widely used method is a CGH-based approach implemented with an SLM and a 4f optical setup15. In Fig. 2, a photon with a Gaussian spatial profile

emitted from a laser is sent to a phase SLM, displaying a CGH pattern to generate OAM states, each carrying a phase factor \(e^{i l\theta }\) which depends on the azimuthal angle \(\theta \)

and the OAM number _l_. _l_ could be any integer, but when all generated _l_ are expected to be positive, the output photon is described by the state: $$\begin{aligned} \begin{aligned}

SLM(\phi _1,\phi _2,\ldots ,\phi _K){|{0}\rangle } = \frac{1}{\sqrt{K}}\sum ^{K}_{l=1}e^{i\phi _l}{|{+l}\rangle } \end{aligned} \end{aligned}$$ (2) where \(\phi _1, \phi _2, \ldots , \phi

_K\) depict phase changes associated with each OAM with _l_ values being +1, +2, \(\ldots \), and \(+K\), respectively, and \({|{l}\rangle }\) denotes the photon state with OAM value of _l_.

That is to say, a single photon is emitted from the source system that contain _K_ OAM states with equal probability amplitude. Meanwhile, a mirror causes flipping of the twisted structure

of any given OAM; that is, the function of a beam splitter (BS) in the light propagation is represented by $$\begin{aligned} \begin{aligned} {|{\Phi }\rangle }\xrightarrow {1:1 \ beam \

splitter} \frac{1}{\sqrt{2}}{|{\Phi }\rangle }_{transmitted} + \frac{i}{\sqrt{2}}R{|{\Phi }\rangle }_{reflected}, \end{aligned} \end{aligned}$$ (3) where _R_ represents flipping of OAM

state, for example, \(R{|{+1}\rangle }={|{-1}\rangle }\). In the case \(K=3\), we generate a photon state that carries equally \(l=+1, +2, +3\) by setting \(\phi _1=\phi _2=\phi _3=0\). That

is, the output after SLM is given by \((1/\sqrt{3}) \times ({|{+1}\rangle }+{|{+2}\rangle }+{|{+3}\rangle })\). This photon is then transferred to an array of BSs and single photon

detection system to examine which _l_-valued OAM is detected. Among a variety of methods in measuring the OAM of light31, the system architecture shown in Fig. 2 illustrates a method

utilizing a hologram (HG) followed by a zeroth-order extraction system32. In practical implementation, a zeroth-order extraction system could be free-space optics with spatial filtering or

single-mode optical fibre. This hologram adds a phase factor of \(e^{i l_{HG} \theta }\) to the state \({|{l}\rangle }\) with OAM _l_, which results in a transformation \({|{l}\rangle }

\rightarrow {|{l+l_{HG}}\rangle }\). After injection into a zeroth-order extraction system, only an \(l=0\) photon propagates in it. In other words, the zeroth-order extraction system acts

as a filter to extract the \(l=0\) component only. If the hologram induces a shift of OAM by \(l_{HG}\) and a photon is detected by the subsequent photodetector, the OAM of the incoming

photon is identified to be \(l = -l_{HG}\). Based on this principle, in the system shown in Fig. 2, three holograms HG1, HG2, HG3 are arranged, which transform \({|{l}\rangle }\) into

\({|{l-1}\rangle }, {|{l-2}\rangle }\), and \({|{l-3}\rangle }\), respectively. One remark here is that, although multiple BSs and holograms are employed in Fig. 2, more compact realization

is indeed possible by, for example, a geometric optical transformation technique33, which has been extended to more than 50 OAM states34. The reason behind the introduction of the

measurement architecture shown in Fig. 2 regards the following procedure related to photon detections. The output light is subjected to attenuators (ATT1, ATT2, ATT3) to control detection

probabilities and a zeroth-order extraction system, followed by photodetectors (PD1, PD2, PD3). Based on the filtering by the zeroth-order extraction system, photon detection by PD1, PD2,

and PD3 means observing OAM values of 1, 2, and 3, respectively. Photon detection by PD1 immediately means playing slot machine 1. Similarly, PD2 and PD3 are associated with the decision of

playing slot machines 2 and 3, respectively. It should be emphasized that in this configuration, a machine is only selected if a photon is detected. Initially, since the probabilities of the

detected photons to be measured by PD1, PD2, and PD3 are all equal to 1/3, all machines are explored equally. Depending on the obtained results, the attenuation levels by ATT1, ATT2, ATT3

are updated. After a single photon is detected by any photodetector, the selection yields eventual rewards from slot machines, and the results are registered into history _H_(_t_). While

referring to the history _H_(_t_), the next decision is determined by following a certain policy of the player. The softmax policy is one of the most well-known feedback algorithms for the

decision, which is also considered to accurately emulate the model of human decision making35,36. In the softmax policy, the player selects each machine based on a maximum likelihood

estimation of the reward probability \({\hat{P}}_1(t),{\hat{P}}_2(t),\ldots ,{\hat{P}}_K(t)\) and the probability of selecting machine _i_ is given by the following equation:

$$\begin{aligned} \begin{aligned} s_i(t+1)&= \frac{e^{\beta {\hat{P}}_i(t)}}{\displaystyle {\sum _{k=1}^{K}}e^{\beta {\hat{P}}_k(t)}} \end{aligned} \end{aligned}$$ (4) where \(\beta \),

which is also known as inverse temperature from analogy to statistical mechanics, is a parameter that influences the balance between exploration and exploitation. While optimal parameter

\(\beta \) depends on reward probabilities and some methods for tuning \(\beta \) have been proposed37, this paper, for simplicity, set it to a constant value \(\beta = 20\) based on a

moderate tuning. The amplitude transmittance of attenuators (ATT1, ATT2, ATT3) are denoted by \(d_1, d_2, d_3\), which are initially all one. These values are updated after every trial based

on: $$\begin{aligned} \begin{aligned} d_i(t) = \sqrt{\frac{s_i(t)}{\displaystyle {\max _{k}}{s_k(t)}}}. \end{aligned} \end{aligned}$$ (5) In this way, \(d_{i}(t)\) is revised as the time

elapses so that the photon detection event is highly likely induced at the photodetector that corresponds to the best slot machine or the highest reward probability machine. For example, if

slot machine 1 is the highest reward probability one, the transmittance of ATT1 should be higher while those of ATT2 and ATT3 should become smaller. Here is a remark about the denominator of

the right side of Eq. (5). The probability of detecting state _i_ is proportional to \(d_i(t)^2\). Dividing each \(d_i(t)^2\) by the same value \(\displaystyle {\max _{k}}{s_k(t)}\) does

not give any unintended bias to the detection probabilities, but transmission efficiency by the attenuators is kept high. That is, the loss of photons by the attenuators is minimized.

Finally, we discuss one more important remark regarding the architecture for solving the single-player, multi-armed bandit problem shown in Fig. 2. The principle maximizes the detection

probability of the OAM state corresponding to the best machine. Actually, instead of reconfiguring the attenuators, we can accomplish the same functionality by reconfiguring the phase

pattern displayed at the SLM located on the light source side. Indeed, this alternative way is directly and dynamically utilizing the high-dimensional property of OAM38. This architecture,

however, imposes a complex arbitration mechanism when we extend the principle to two-player situations in the following. That is, controlling the light source by a single player is indeed

feasible, but the source management by two players is non-trivial. Instead, player-specific attenuator control does not impose any global server. For these reasons, we discuss the

fundamental architecture shown in Fig. 2. SIMULATION RESULTS FOR 1-PLAYER 3-ARMED BANDIT PROBLEM Figure 3 summarizes simulation results for the 1-player 3-armed bandit problem with the OAM

system following the softmax policy. The solid, dashed, and dashed-dotted curves in Fig. 3a show the time evolution of the selection probability of machine 1, 2, and 3, respectively, when

the reward probability of slot machines are given by \([P_1, P_2, P_3] = [0.9, 0.7, 0.1]\). Here the number of repetitions is 1000. We can clearly observe that the probability of selecting

the maximum reward probability machine, here machine 1, monotonically increases. Figure 3b examines the correct decision rate, which is referred to as CDR, defined by the number of

selections of the highest reward probability machine over 1000 trials when the reward environment is configured differently. The blue, red, and yellow curves show the time evolution of CDR

when the reward environment \([P_1, P_2, P_3]\) is given by [0.9, 0.7, 0.1], [0.9, 0.5, 0.1], and [0.9, 0.3, 0.1], respectively. Here the maximum and minimum reward probabilities are

commonly configured. As the difference between the maximum and the second maximum reward probability becomes smaller, the increase of CDR toward unity becomes slow. Nevertheless, we can

observe that the monotonic increase of selecting the best machine in Figs. 3a,b. Since there is no theoretical limitation regarding the number of OAM states, the system configuration herein

can be used for the probabilistic selection among a large number of selections. Note that the softmax policy itself is also scalable. SOLVING 2-PLAYER 3-ARMED BANDIT PROBLEM WITH OAM AND

QUANTUM INTERFERENCE SYSTEM ARCHITECTURE FOR SOLVING 2-PLAYER 3-ARMED COMPETITIVE BANDIT PROBLEM WITH OAM AND QUANTUM INTERFERENCE This section discusses stochastic selections of arms in the

CMAB problem using photon pair OAM quantum states. The system presented in Fig. 2 has been extended to the case of two players (Player A and B) by the architecture represented in Fig. 4.

This time, the assumption is that the selection only happens when exactly one photon is detected simultaneously by each player on their photodetectors. In the source part, a photon pair is

created by a nonlinear crystal such as a periodically poled KTP (PPKTP) and then subjected to an interferometer. One of the photon pair is supplied to the Detection A system, and the other

goes to the Detection B system. The internal structure of Detection systems is the same as the one-player system depicted in Fig. 2. Thanks to the quantum interference, even though there is

no explicit communication between the players, the detection results of the two photons are correlated with each other, as discussed in detail later. In quantum research using light, it has

been common to use quantum states based on properties such as polarization, spatial mode, and phase, but since the discovery of orbital angular momentum, many studies on quantum states using

orbital angular momentum of light have been reported39. The availability of orbital angular momentum with an infinite number of states is very important in quantum research. In 2001, Mair

et al. used parametric down conversion (PDC) to study the generation of photon pairs in states with entangled orbital angular momentum39. Subsequently, a theoretical study of the change in

orbital angular momentum during the PDC process was performed40, and photon pairs with three entangled orbital angular momentum states were also studied41. In the present study, we utilize

quantum interference given by an extension of the Hong-Ou-Mandel effect22. GENERATION OF OAM PHOTON PAIR WITH QUANTUM INTERFERENCE Hong-Ou-Mandel effect has been well studied for two

identical photons always detected together in the same output path when they enter into a 1:1 beam splitter22. We extend the description of this phenomenon for multiple-OAM states carrying

input photons. When OAM states of input photon \({|{\Phi }\rangle }\) is sent to the beam splitter, transmitted term A and reflected term B can be described with the following forms:

$$\begin{aligned} \begin{aligned} {|{\Phi }\rangle }\xrightarrow {1:1 \ beam \ splitter} \frac{1}{\sqrt{2}}{|{\Phi }\rangle }_A + \frac{i}{\sqrt{2}}R{|{\Phi }\rangle }_B. \end{aligned}

\end{aligned}$$ (6) where _R_ represents flipping of OAM state, for example, \(R{|{+1}\rangle }={|{-1}\rangle }\). As shown in Fig. 5a, when OAM states of input photons are \({|{\Phi

}\rangle },{|{\Psi }\rangle }\) on the two BS inputs, the output state \({|{\Phi '}\rangle }\otimes {|{\Psi '}\rangle }\) can be described with the following forms:

$$\begin{aligned} \begin{aligned} {|{\Phi '}\rangle }\otimes {|{\Psi '}\rangle }&= \left( \frac{1}{\sqrt{2}}{|{\Phi }\rangle }_A + \frac{i}{\sqrt{2}}R{|{\Phi }\rangle }_B

\right) \otimes \left( \frac{i}{\sqrt{2}}R{|{\Psi }\rangle }_A + \frac{1}{\sqrt{2}}{|{\Psi }\rangle }_B \right) \\&= \left( \frac{i}{2}{|{\Phi }\rangle }_A\otimes R{|{\Psi }\rangle

}_A\right) + \left( \frac{1}{2}{|{\Phi }\rangle }_A\otimes {|{\Psi }\rangle }_B - \frac{1}{2}R{|{\Psi }\rangle }_A\otimes R{|{\Phi }\rangle }_B\right) + \left( \frac{i}{2}R{|{\Phi }\rangle

}_B\otimes {|{\Psi }\rangle }_B\right) . \end{aligned} \end{aligned}$$ (7) With _K_ being the number of OAM used in the system, the input states \({|{\Phi }\rangle },{|{\Psi }\rangle }\) can

be set to $$\begin{aligned} \begin{aligned} {|{\Phi }\rangle } = \frac{1}{\sqrt{K}}\sum ^{K}_{k=1}e^{i\phi _k}{|{+k}\rangle }, \ \ \ {|{\Psi }\rangle } = \frac{1}{\sqrt{K}}\sum

^{K}_{k=1}e^{i\psi _k}{|{-k}\rangle }, \end{aligned} \end{aligned}$$ (8) considering that the two photons have the same polarization, wavelength, and are synchronized on the beam splitter.

Each term of the output state given by Eq. (7) is described by the following: $$ \begin{aligned} |\Phi \rangle _{A} \otimes R|\Psi \rangle _{A} & = \left( {\sum\limits_{{k = 1}}^{K}

{\frac{1}{{\sqrt K }}} e^{{i\phi _{k} }} | + k\rangle _{A} } \right) \otimes \left( {\sum\limits_{{k = 1}}^{K} {\frac{1}{{\sqrt K }}} e^{{i\psi _{k} }} | + k\rangle _{A} } \right) \\ & =

\sum\limits_{{k = 1}}^{K} {\frac{1}{K}} e^{{i(\phi _{k} + \psi _{k} )}} | + k\rangle _{A} \otimes | + k\rangle _{A} + \sum\limits_{{k_{1} < k_{2} }}^{K} {\frac{1}{K}\left( {e^{{i(\phi

_{{k_{1} }} + \psi _{{k_{2} }} )}} + e^{{i(\psi _{{k_{1} }} + \phi _{{k_{2} }} )}} } \right)| + k_{1} \rangle _{A} \otimes | + k_{2} \rangle _{A} } \\ \end{aligned} $$ (9) $$ \begin{aligned}

|\Phi \rangle _{A} \otimes |\Psi \rangle _{B} - R|\Psi \rangle _{A} \otimes R|\Phi \rangle _{B} & = \sum\limits_{{k = 1}}^{K} {\frac{1}{{\sqrt K }}} e^{{i\phi _{k} }} | + k\rangle _{A}

\otimes \sum\limits_{{k = 1}}^{K} {\frac{1}{{\sqrt K }}} e^{{i\psi _{k} }} | - k\rangle _{B} - \sum\limits_{{k = 1}}^{K} {\frac{1}{{\sqrt K }}} e^{{i\psi _{k} }} | + k\rangle _{A} \otimes

\sum\limits_{{k = 1}}^{K} {\frac{1}{{\sqrt K }}} e^{{i\phi _{k} }} | - k\rangle _{B} \\ & = \sum\limits_{{k_{1} = 1}}^{K} {\sum\limits_{{k_{2} = 1}}^{K} {\frac{1}{K}} } e^{{i(\phi

_{{k_{1} }} + \psi _{{k_{2} }} )}} | + k_{1} \rangle _{A} \otimes | - k_{2} \rangle _{B} - \sum\limits_{{k_{1} = 1}}^{K} {\sum\limits_{{k_{2} = 1}}^{K} {\frac{1}{K}} } e^{{i(\psi _{{k_{1} }}

+ \phi _{{k_{2} }} )}} | + k_{1} \rangle _{A} \otimes | - k_{2} \rangle _{B} \\ & = \sum\limits_{{k_{1} = 1}}^{K} {\sum\limits_{{k_{2} = 1}}^{K} {\frac{1}{K}} } \left( {e^{{i(\phi

_{{k_{1} }} + \psi _{{k_{2} }} )}} - e^{{i(\psi _{{k_{1} }} + \phi _{{k_{2} }} )}} } \right)| + k_{1} \rangle _{A} \otimes | - k_{2} \rangle _{B} .{\text{ }} \\ \end{aligned} $$ (10)

Therefore, the output state \({|{\Phi '}\rangle }\otimes {|{\Psi '}\rangle }\) is given by the following terms: $$\begin{aligned} \begin{aligned} {|{\Phi '}\rangle }\otimes

{|{\Psi '}\rangle }&= \sum _{k=1}^{K}\frac{i}{2K}e^{i(\phi _k+\psi _k)}{|{+k}\rangle }_A\otimes {|{+k}\rangle }_A \\&+\sum _{k_1< k_2}^{K}\frac{i}{2K}\left( e^{i(\phi

_{k_1}+\psi _{k_2})}+e^{i(\psi _{k_1}+\phi _{k_2})}\right) {|{+k_1}\rangle }_A\otimes {|{+k_2}\rangle }_A \\&+\sum _{k_1=1}^{K}\sum _{k_2=1}^{K}\frac{1}{2K}\left( e^{i(\phi _{k_1}+\psi

_{k_2})}-e^{i(\psi _{k_1}+\phi _{k_2})}\right) {|{+k_1}\rangle }_A\otimes {|{-k_2}\rangle }_B \\&+\sum _{k=1}^{K}\frac{i}{2K}e^{i(\phi _k+\psi _k)}{|{-k}\rangle }_B\otimes {|{-k}\rangle

}_B \\&+\sum _{k_1 < k_2}^{K}\frac{i}{2K}\left( e^{i(\phi _{k_1}+\psi _{k_2})}+e^{i(\psi _{k_1}+\phi _{k_2})}\right) {|{-k_1}\rangle }_B\otimes {|{-k_2}\rangle }_B. \end{aligned}

\end{aligned}$$ (11) Correspondingly, the probability of detecting the same state at the same side, that is \({|{+k}\rangle }_A\otimes {|{+k}\rangle }_A\) or \({|{-k}\rangle }_B\otimes

{|{-k}\rangle }_B\), is given by $$\begin{aligned} \begin{aligned} 2\cdot \left| \frac{i}{2K}e^{i(\phi _k+\psi _k)}\right| ^2 = \frac{1}{2K^2}. \end{aligned} \end{aligned}$$ (12) By

introducing parameters \(\theta _k=\frac{\phi _k-\psi _k}{2}\), which depends on the phase difference of two input states, the probability of detecting different states on the same side,

that is \({|{+k_1}\rangle }_A\otimes {|{+k_2}\rangle }_A\) or \({|{-k_1}\rangle }_B\otimes {|{-k_2}\rangle }_B\), is given by $$\begin{aligned} \begin{aligned} \left| \frac{i}{2K}\left(

e^{i(\phi _{k_1}+\psi _{k_2})}+e^{i(\psi _{k_1}+\phi _{k_2})}\right) \right| ^2 = \frac{1}{K^2}\cos ^2(\theta _{k_1}-\theta _{k_2}), \end{aligned} \end{aligned}$$ (13) and finally the

probability of detecting pair of states on different sides, that is \({|{+k_1}\rangle }_A\otimes {|{-k_2}\rangle }_B\), is given by $$\begin{aligned} \begin{aligned} \left|

\frac{1}{2K}\left( e^{i(\phi _{k_1}+\psi _{k_2})}-e^{i(\psi _{k_1}+\phi _{k_2})}\right) \right| ^2 = \frac{1}{K^2}\sin ^2(\theta _{k_1}-\theta _{k_2}). \end{aligned} \end{aligned}$$ (14)

Figure 5b summarizes the probability of detecting each output state, while Fig. 6 shows all the probabilities with _K_ ranging from 1 to 4. The probabilities depend only on \(\theta _k\),

which can be tuned by controlling the SLM phases \(\phi _k\) and \(\psi _k\). A pair of photons being detected on both sides is displayed with the red frames in Fig. 6, which are utilized as

selections by the two players. What is remarkable is that the probability of detecting the same states at different sides is always zero because the probability term \(\sin ^2(\theta

_k-\theta _k)\) is always equal to zero. For \(K=1\), this phenomenon corresponds to what is known as the Hong-Ou-Mandel effect. As the detected OAM states correspond to the selection of

players, the probability of both players selecting the same machine is only limited by experimental constraints such as multiple pair generation, meaning that conflict-free decisions are

accomplished. The probabilities described in the red frames include the probabilities of detecting different states by the two players. It is remarkable that these probabilities can take

equal value when _K_ is less than or equal to three. For example, when \(K = 2\), by assigning \(\theta _1 = 0\) and \(\theta _2 = \pi /2\), all such probabilities becomes 1/4. Similarly,

when \(K = 3\), by setting \((\theta _1, \theta _2, \theta _3) = (0, \pi /3, 2\pi /3)\), the probabilities are all 1/12. Namely, all arm combinations except selecting the same arm are

selected equally. Note, however, that when _K_ is larger or equal to four, we cannot perfectly equalize these probabilities by only tuning \(\theta _1,\theta _2,\ldots ,\theta _K\). This

point is discussed in the “Discussion” section. In this study, we focus on the case when \(K = 3\) because the equivalent selection of pairs is ensured, as discussed above. SIMULATION

RESULTS FOR 2-PLAYER 3-ARMED BANDIT PROBLEM In the CMAB problem in the present study, the rewards are equally split among the players who selected the same machine; that is, the decision

conflict by multiple players reduces the individual benefit. Furthermore, total rewards are reduced because of the conflicted choice. Here we begin with a brief overview of the two-player

decision-making situations by a game-theoretic formalism42 while mentioning its intuitive implications. We denote \(P_{k^{*}}, P_{k^{**}}, P_{k^{***}}\) respectively the first, second, and

third highest reward probability. First, when \(P_{k^{*}} > 2\times P_{k^{**}}\), the situation of both players selecting machine 1 is the only Nash equilibrium. That is, conflict is

unavoidable if both players act in a greedy manner because the best machine is far better than the other machines. Second, when \(P_{k^{*}}<2 \times P_{k^{**}}\), Nash equilibrium is

achieved when player 1 chooses the best machine (machine \(k^{*}\)), and player 2 selects the second-best machine (machine \(k^{**}\)), and vice versa. That is, conflicting decisions are

avoided because changing the player’s decision decreases his/her reward. However, there is a problem from the viewpoint of equality, as one of the players can keep selecting the higher

reward machines while the other is locked with the lower reward decisions. Third, there exists another symmetric Nash equilibrium with a mixed strategy, meaning that they select each machine

with a certain probability. The details are described in the “Methods” section. Intuitively speaking, by this mixed strategy, both players sometimes intentionally refrain from choosing the

best machine. Therefore, sometimes, decision conflicts can be avoided. Indeed, Lai et al. successfully utilized a mixed strategy in dynamic channel selection in communication systems7.

However, it should be remarked that perfect conflict avoidance cannot be ensured by mixed strategies. In order to quantitatively evaluate the performance differences among different

policies, we compare the quantum interference system with the following two policies. One is a greedy policy where both players take greedy actions as if they are playing alone. The second

is an equilibrium policy where both players try to achieve the symmetric Nash equilibrium by a mixed strategy. The details are described in the “Methods” section. Figure 7 shows the results

for solving the 2-player 3-armed bandit problem. Figure 7a shows how the selection probabilities of both players evolve with each policy. With the greedy policy, reminding that machine 1 has

the highest reward probability of 0.9, its selection probability approaches almost 1 for both players, as in the case of a single player. For the equilibrium policy, the selection

probabilities of the two most rewarding machines 1 and 2 converge to the probabilities defined by the mixed strategy. With the quantum interference strategy, however, machine 1 and machine 2

are selected with equal probability by both players. Figure 7b shows the ratio of each selection combination from both players. The greedy policy is associated with a large number of

conflicts as both players almost only select machine 1, while the equilibrium policy reduces the number of conflicts to some extent as the selections are distributed. Finally, the quantum

interference policy completely avoids conflicts. The final rewards with such selections are shown in Fig. 7c, for each player and for the total attributed reward. We observe that the quantum

interference policy achieves almost ideal total rewards as well as equality between players. By contrast, the total reward by the greedy and the equilibrium policies becomes small compared

with the quantum interference policy because they suffer from unavoidable decision conflicts. Figure 7d shows how the final reward of each policy varies when the reward probabilities of the

three machines are modified. In greedy and equilibrium policies, the total reward changes due to the rate of selection of the lowest rewarding machine 3 in the exploration phase. On the

other hand, with the quantum interference policy, the larger the difference between the reward probabilities of machine 2 and machine 3, the easier it is to determine the top two machines,

and the higher the final total reward; despite this, the difference in total reward is mild in comparison with the difference with the other two policies. DISCUSSION In this study, we show

that we can benefit from the high dimensionality of OAM for scalability in solving multi-armed bandit problems. Furthermore, appropriate quantum interference constructions lead to achieving

high rewards while maintaining a fair repartition between two players in competitive bandit problem situations. The total reward optimization is guaranteed by the selections of the two best

machines by the two players in a non-conflicting manner, while the fair repartition is guaranteed by the equal probabilities of selection among players through quantum interference. The main

assumption is the simultaneous detection of exactly one photon for all players. In the proposed optical design, this is for the purpose of the extended Hong-Ou-Mandel effect or quantum

interference that guarantees that identical photons go to the same side of the beam splitter, at the price of a post-selection of half of all photon pairs. While this is a strong constraint

for potential applications, this design is only an example, and nothing forbids the obtention of the target state with other designs that do not rely on post-selection. Regarding the

extension to more arms, the current design is limited to three arms due to fundamental constraints (lack of enough degrees of freedom to constrain the 2-photon state). This may be solved by

allowing to tune the relative amplitude between each OAM with the SLM and/or additional mechanisms. Once again, the goal of the setup presented in this study is only to present the principle

of utilizing OAM for multiple arms in MAB and quantum interference for competitive decision-making. We believe that the extension to many arms is a technological problem without theoretical

constraints34. The next discussion point is about security. The two-player CMAB system herein intends to let the players directly influence the detection probability via the attenuation

amplitude in front of the detectors. While this architecture ensures independent machine selection and revision of the attenuation among the players, it presents one fundamental weakness: if

a player only wants to select the highest rewarding arm, then the attenuation will be maximized for the lower arms, only letting photons reach the corresponding detector. However, this

situation is easily identifiable by the other player, who can recognize that the probability of selecting a particular machine decreases. The solution for that player is straightforward:

attenuate more the second-best arm too to correct the imbalance (in case of slight inequality), which is equivalent to not playing anymore if the other player completely blocks the other

photons. This brings the following discussion point about the photon utilization efficiency. In this study, only simultaneous detection of exactly one photon for all detectors of each and

every player triggers the selection of arms from both players. The reason is to implement the post-selection of output states where one photon goes for both players instead of two photons

for only one player. With the current operation principle based on quantum interference summarized in Fig. 6, half of all photon pairs are strictly unusable for the players. Although such a

loss is unavoidable, further photon losses are induced in the system architecture shown in Fig. 4 because of the multiple BSs. As discussed earlier, this part can be improved by

technological methods developed in the literature33,34. CONCLUSION To overcome the scalability limitations in the former single-photon-based decision making that relies on two orthogonal

polarizations to resolve the two-armed bandit problem, we associate orbital angular momentum of photons to individual arms, which theoretically allows ideal scalability. When multiple

players are involved, conflict of decisions becomes a serious issue, which is known as the competitive multi-armed bandit problem. Formerly, polarization-entangled photons have been shown to

realize conflict-free decision making in two-player, two-armed situations; however, its arm-scalability is limited to only two. In this study, by extending the Hong-Ou-Mandel effect to more

than two states, we theoretically establish an experimental configuration able to generate quantum interference among states with orbital angular momentum and conditions that provide

conflict-free selections. We numerically examine total rewards regarding two-player, three-armed bandit problems, for which the proposed principle accomplishes almost the theoretical

maximum, which is greater than a conventional mixed strategy intending to realize Nash equilibrium. This study paves a way toward photon-based intelligent systems as well as extending the

utility of the high dimensionality of orbital angular momentum of photons and quantum interference in artificial intelligence domains. METHODS DETAIL ALGORITHM OF GREEDY POLICY, EQUILIBRIUM

POLICY, AND ENTANGLEMENT POLICY GREEDY POLICY (STRATEGTY FOR SINGLE PLAYER MAB) Both players independently decide the probability of selecting each machine at each round. The algorithm is

based on the softmax policy5 and the probability of selecting machine _i_ at round _t_ is given by the following equation: $$\begin{aligned} \begin{aligned} s_k(t+1)&= \frac{e^{\beta

{\hat{P}}_k(t)}}{\displaystyle {\sum _{n=1}^{K}}e^{\beta {\hat{P}}_n(t)}}. \end{aligned} \end{aligned}$$ (15) If there exists a non-selected machine, all the machines are selected randomly

with the same probability. Otherwise, \({\hat{P}}_k(t)=\frac{w_k(t)}{w_k(t)+l_k(t)}\) when the player has been rewarded \(w_k(t)\) times and not rewarded \(l_k(t)\) times from machine _k_.

As a moderate tuning, \(\beta \) is set to be 20 in this study. EQUILIBRIUM POLICY Table1 represents the profit table of the expected reward in a single selection. In Nash equilibrium, no

player has anything to gain by changing only their own strategy. In Nash equilibrium, the strategy may be selecting one particular machine, but it could also be a strategy such that multiple

machines are probabilistically chosen. In the situation of Table 1, strategies can be defined with the probabilities of selecting machine 1, machine 2, machine 3, or \(\alpha _1,\alpha

_2,\alpha _3\) for player A and \(\beta _1,\beta _2,\beta _3\) for player B. In what follows, the notations \(k^{*},k^{**},k^{***}\) represent indices of the first, the second, and the third

best machine, respectively. Nash equilibriums are summarized as shown below: * in case \(P_{k^{*}}>2P_{k^{**}}\) * \(\diamond \) \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}}) =

(\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) = (1,0,0)\) * in case \(P_{k^{*}}<2P_{k^{**}}\) and \(P_{k^{*}}P_{k^{**}}/Q>\frac{2}{5}\) * \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha

_{k^{***}}) = (1,0,0), \ (\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) = (0,1,0)\) * \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}}) = (0,1,0), \ (\beta _{k^{*}},\beta

_{k^{**}},\beta _{k^{***}}) = (1,0,0)\) * \(\diamond \) \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}}) = (\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) =

(\frac{2P_{k^{*}}-P_{k^{**}}}{P_{k^{*}}+P_{k^{**}}}, \frac{2P_{k^{**}}-P_{k^{*}}}{P_{k^{*}}+P_{k^{**}}},0)\) * in case \(P_{k^{*}}<2P_{k^{**}}\) and

\(P_{k^{*}}P_{k^{**}}/Q<\frac{2}{5}\) * \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}}) = (1,0,0), \ (\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) = (0,1,0)\) * \((\alpha

_{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}}) = (0,1,0), \ (\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) = (1,0,0)\) * \(\diamond \) \((\alpha _{k^{*}},\alpha _{k^{**}},\alpha _{k^{***}})

= (\beta _{k^{*}},\beta _{k^{**}},\beta _{k^{***}}) = (2 - \frac{5P_{k^{**}}P_{k^{***}}}{Q}, 2 - \frac{5P_{k^{***}}P_{k^{*}}}{Q}, 2 - \frac{5P_{k^{*}}P_{k^{**}}}{Q})\) where \(Q =

P_{k^{*}}P_{k^{**}}+P_{k^{**}}P_{k^{***}}+P_{k^{***}}P_{k^{*}}\). With the equilibrium policy, both players try to achieve symmetric Nash equilibrium, which is represented with the shape

\(\diamond \) above, under the situation that reward probabilities are not quite sure. In the simulation algorithm, each player decides which machines are better and which Nash equilibrium

to achieve based on their own maximum likelihood estimation of reward probabilities. In an actual algorithm, the parameters of player 1 are calculated as below with \({\hat{k}}^{*},

{\hat{k}}^{**}, {\hat{k}}^{***}\) respectively representing machine indices with the first, the second, and the third highest estimated reward probability: * in case

\({\hat{P}}_{{\hat{k}}^{*}}>2{\hat{P}}_{{\hat{k}}^{**}}\) * \((\alpha ^{*},\alpha ^{**},\alpha ^{***}) = (1,0,0)\) * in case \({\hat{P}}_{{\hat{k}}^{*}}>2{\hat{P}}_{{\hat{k}}^{**}}\)

and \({\hat{P}}_{{\hat{k}}^{*}}{\hat{P}}_{{\hat{k}}^{**}}/Q>\frac{2}{5}\) * \((\alpha ^{*},\alpha ^{**},\alpha ^{***}) =

(\frac{2{\hat{P}}_{{\hat{k}}^{*}}-{\hat{P}}_{{\hat{k}}^{**}}}{{\hat{P}}_{{\hat{k}}^{*}}+{\hat{P}}_{{\hat{k}}^{**}}},

\frac{2{\hat{P}}_{{\hat{k}}^{**}}-{\hat{P}}_{{\hat{k}}^{*}}}{{\hat{P}}_{{\hat{k}}^{*}}+{\hat{P}}_{{\hat{k}}^{**}}},0)\) * in case \({\hat{P}}_{{\hat{k}}^{*}}<2{\hat{P}}_{{\hat{k}}^{**}}\)

and \({\hat{P}}_{{\hat{k}}^{*}}{\hat{P}}_{{\hat{k}}^{**}}/Q<\frac{2}{5}\) * \((\alpha ^{*},\alpha ^{**},\alpha ^{***}) = (2 -

\frac{5{\hat{P}}_{{\hat{k}}^{**}}{\hat{P}}_{{\hat{k}}^{***}}}{Q}, 2 - \frac{5{\hat{P}}_{{\hat{k}}^{***}}{\hat{P}}_{{\hat{k}}^{*}}}{Q}, 2 -

\frac{5{\hat{P}}_{{\hat{k}}^{*}}{\hat{P}}_{{\hat{k}}^{**}}}{Q})\) where \(Q =

{\hat{P}}_{{\hat{k}}^{*}}{\hat{P}}_{{\hat{k}}^{**}}+{\hat{P}}_{{\hat{k}}^{**}}{\hat{P}}_{{\hat{k}}^{***}}+{\hat{P}}_{{\hat{k}}^{***}}{\hat{P}}_{{\hat{k}}^{*}}\), and

\({\hat{P}}_{{\hat{k}}^{*}},{\hat{P}}_{{\hat{k}}^{**}},{\hat{P}}_{{\hat{k}}^{***}}\) represent the first, the second, and the third highest estimated reward probability. The parameters of

player 2 are also calculated in the same way with the different reward probability estimations. The probability of selecting each machine is calculated as below: $$\begin{aligned}

\begin{aligned} s_{{\hat{k}}^{*}}(t+1)&= \alpha ^{*}\pi (P_{{\hat{k}}^{*}}=P_{k^{*}}|H(t)) + \alpha ^{**}\pi (P_{{\hat{k}}^{*}}=P_{k^{**}}|H(t)) + \alpha ^{***}\pi

(P_{{\hat{k}}^{*}}=P_{k^{***}}|H(t)) \\ s_{{\hat{k}}^{**}}(t+1)&= \alpha ^{*}\pi (P_{{\hat{k}}^{**}}=P_{k^{*}}|H(t)) + \alpha ^{**}\pi (P_{{\hat{k}}^{**}}=P_{k^{**}}|H(t)) + \alpha

^{***}\pi (P_{{\hat{k}}^{**}}=P_{k^{***}}|H(t)) \\ s_{{\hat{k}}^{***}}(t+1)&= \alpha ^{*}\pi (P_{{\hat{k}}^{***}}=P_{k^{*}}|H(t)) + \alpha ^{**}\pi (P_{{\hat{k}}^{***}}=P_k{^{**}}|H(t))

+ \alpha ^{***}\pi (P_{{\hat{k}}^{***}}=P_{k^{***}}|H(t)) \end{aligned} \end{aligned}$$ (16) where, \(\pi (P_{{\hat{k}}^{*}}=P_{k^{*}}|H(t))\) represents the probability of machine

\({\hat{k}}^{*}\) to have the highest reward probability from the estimation based on the softmax policy. Here, \(\pi (P_a>P_b>P_c|H(t))\) represents the probability of reward

probabilities being \(P_a>P_b>P_c\) under this estimation and it is calculated as below: $$\begin{aligned} \begin{aligned} \pi (P_a>P_b>P_c|H(t)) = \frac{e^{\beta

{\hat{P}}_a}}{e^{\beta {\hat{P}}_a}+e^{\beta {\hat{P}}_b}+e^{\beta {\hat{P}}_c}}\cdot \frac{e^{\beta {\hat{P}}_b}}{e^{\beta {\hat{P}}_b}+e^{\beta {\hat{P}}_c}}. \end{aligned} \end{aligned}$$

(17) Therefore, probabilities of \(P_a\) being the first, the second, and the third best machine under estimation with softmax policy are: $$\begin{aligned} \begin{aligned} \pi

(P_a=P_{k^{*}}|H(t)) = \pi (P_a>P_b>P_c|H(t)) + \pi (P_a>P_c>P_b|H(t)) \\ \pi (P_a=P_{k^{**}}|H(t)) = \pi (P_b>P_a>P_c|H(t)) + \pi (P_c>P_a>P_b|H(t)) \\ \pi

(P_a=P_{k^{***}}|H(t)) = \pi (P_b>P_c>P_a|H(t)) + \pi (P_c>P_b>P_a|H(t)). \end{aligned} \end{aligned}$$ (18) QUANTUM INTERFERENCE POLICY In the quantum interference policy, both

players try to select both the first and the second-best machine with the same probability to achieve fairness between the two players. Therefore, the probabilities of selecting machines are

given by the following equation: $$\begin{aligned} \begin{aligned} s_{k}(t+1)&= \frac{1}{2}\left( \pi (P_k=P_{k^{*}}|H(t)) + \pi (P_k=P_{k^{**}}|H(t))\right) . \end{aligned}

\end{aligned}$$ (19) REFERENCES * Kitayama, K. _et al._ Novel frontier of photonics for data processing-photonic accelerator. _APL Photonics_ 4, 090901 (2019). Article  ADS  Google Scholar 

* De Lima, T. F. _et al._ Machine learning with neuromorphic photonics. _J. Lightwave Technol._ 37, 1515–1534 (2019). Article  ADS  Google Scholar  * Shen, Y. _et al._ Deep learning with

coherent nanophotonic circuits. _Nat. Photonics_ 11, 441 (2017). Article  ADS  CAS  Google Scholar  * Van der Sande, G., Brunner, D. & Soriano, M. C. Advances in photonic reservoir

computing. _Nanophotonics_ 6, 561–576 (2017). Article  Google Scholar  * Sutton, R. S. & Barto, A. G. t al 1st edn. (MIT Press, 1998). MATH  Google Scholar  * Auer, P., Cesa-Bianchi, N.

& Fischer, P. Finite-time analysis of the multiarmed bandit problem. _Mach. Learn._ 47, 235–256 (2002). Article  Google Scholar  * Lai, L., El Gamal, H., Jiang, H. & Poor, H. V.

Cognitive medium access: Exploration, exploitation, and competition. _IEEE Trans. Mob. Comput._ 10, 239–253 (2010). Google Scholar  * Kim, S.-J., Naruse, M. & Aono, M. Harnessing the

computational power of fluids for optimization of collective decision making. _Philosophies_ 1, 245–260 (2016). Article  Google Scholar  * Naruse, M. _et al._ Single-photon decision maker.

_Sci. Rep._ 5, 13253 (2015). Article  ADS  CAS  Google Scholar  * Chauvet, N. _et al._ Entangled-photon decision maker. _Sci. Rep._ 9, 12229 (2019). Article  ADS  Google Scholar  * Chauvet,

N. _et al._ Entangled N-photon states for fair and optimal social decision making. _Sci. Rep._ 10, 20420 (2020). Article  CAS  Google Scholar  * Naruse, M. _et al._ Single photon in

hierarchical architecture for physical decision making: Photon intelligence. _ACS Photonics_ 3, 2505–2514 (2016). Article  CAS  Google Scholar  * Allen, L., Barnett, S. M. & Padgett, M. 

J. _Optical Angular Momentum_ (CRC Press, 2003). * Forbes, A., de Oliveira, M. & Dennis, M. R. Structured light. _Nat. Photonics_ 15, 253–262 (2021). Article  ADS  CAS  Google Scholar  *

Yao, A. M. & Padgett, M. J. Orbital angular momentum: Origins, behavior and applications. _Adv. Opt. Photonics_ 3, 161–204 (2011). Article  ADS  CAS  Google Scholar  * Flamini, F.,

Spagnolo, N. & Sciarrino, F. Photonic quantum information processing: A review. _Rep. Prog. Phys._ 82, 016001 (2019). Article  ADS  CAS  Google Scholar  * Forbes, A. & Nape, I.

Quantum mechanics with patterns of light: Progress in high dimensional and multidimensional entanglement with structured light. _AVS Quantum Sci._ 1, 011701 (2019). Article  ADS  Google

Scholar  * Krenn, M., Malik, M., Erhard, M. & Zeilinger, A. Orbital angular momentum of photons and the entanglement of Laguerre–Gaussian modes. _Phil. Trans. R. Soc. A_ 375, 20150442

(2017). Article  ADS  MathSciNet  Google Scholar  * Zhang, Y. _et al._ Engineering two-photon high-dimensional states through quantum interference. _Sci. Adv._ 2, e1501165 (2016). Article 

ADS  Google Scholar  * Mirhosseini, M. _et al._ High-dimensional quantum cryptography with twisted light. _New J. Phys._ 17, 033033 (2015). Article  ADS  MathSciNet  Google Scholar  *

Molina-Terriza, G., Torres, J. P. & Torner, L. Twisted photons. _Nat. Phys._ 3, 305–310 (2007). Article  CAS  Google Scholar  * Hong, C.-K., Ou, Z.-Y. & Mandel, L. Measurement of

subpicosecond time intervals between two photons by interference. _Phys. Rev. Lett._ 59, 2044 (1987). Article  ADS  CAS  Google Scholar  * Pinheiro, A. R. C. _et al._ Vector vortex

implementation of a quantum game. _JOSA B_ 30, 3210–3214 (2013). Article  ADS  CAS  Google Scholar  * Balthazar, W. F., Passos, M. H. M., Schmidt, A. G. M., Caetano, D. P. & Huguenin, J.

A. O. Experimental realization of the quantum duel game using linear optical circuits. _J. Phys. B_ 48, 165505 (2015). Article  ADS  Google Scholar  * Allen, L., Beijersbergen, M. W.,

Spreeuw, R. & Woerdman, J. Orbital angular momentum of light and the transformation of Laguerre–Gaussian laser modes. _Phys. Rev. A_ 45, 8185 (1992). Article  ADS  CAS  Google Scholar  *

Beijersbergen, M., Coerwinkel, R., Kristensen, M. & Woerdman, J. Helical-wavefront laser beams produced with a spiral phaseplate. _Opt. Commun._ 112, 321–327 (1994). Article  ADS  CAS 

Google Scholar  * Heckenberg, N., McDuff, R., Smith, C. & White, A. Generation of optical phase singularities by computer-generated holograms. _Opt. Lett._ 17, 221–223 (1992). Article 

ADS  CAS  Google Scholar  * Beijersbergen, M. W., Allen, L., Van der Veen, H. & Woerdman, J. Astigmatic laser mode converters and transfer of orbital angular momentum. _Opt. Commun._ 96,

123–132 (1993). Article  ADS  Google Scholar  * Padgett, M., Arlt, J., Simpson, N. & Allen, L. An experiment to observe the intensity and phase structure of Laguerre–Gaussian laser

modes. _Am. J. Phys._ 64, 77–82 (1996). Article  ADS  Google Scholar  * Wang, J. _et al._ Terabit free-space data transmission employing orbital angular momentum multiplexing. _Nat.

Photonics_ 6, 488–496 (2012). Article  ADS  CAS  Google Scholar  * Leach, J., Padgett, M. J., Barnett, S. M., Franke-Arnold, S. & Courtial, J. Measuring the orbital angular momentum of a

single photon. _Phys. Rev. Lett._ 88, 257901 (2002). Article  ADS  Google Scholar  * Vaziri, A., Pan, J.-W., Jennewein, T., Weihs, G. & Zeilinger, A. Concentration of higher dimensional

entanglement: Qutrits of photon orbital angular momentum. _Phys. Rev. Lett._ 91, 227902 (2003). Article  ADS  Google Scholar  * Lavery, M. P. _et al._ Refractive elements for the

measurement of the orbital angular momentum of a single photon. _Opt. Express_ 20, 2110–2115 (2012). Article  ADS  Google Scholar  * Lavery, M. P. _et al._ Efficient measurement of an

optical orbital-angular-momentum spectrum comprising more than 50 states. _New J. Phys._ 15, 013024 (2013). Article  ADS  CAS  Google Scholar  * Cohen, J. D., McClure, S. M. & Yu, A. J.

Should I stay or should I go? how the human brain manages the trade-off between exploitation and exploration. _Philos. Trans. R. Soc. B_ 362, 933–942 (2007). Article  Google Scholar  * Daw,

N. D., O'doherty, J. P., Dayan, P., Seymour, B. & Dolan, R. J. Cortical substrates for exploratory decisions in humans. _Nature_ 441, 876–879 (2006). Article  ADS  CAS  Google

Scholar  * Cesa-Bianchi, N., Gentile, C., Lugosi, G. & Neu, G. Boltzmann exploration done right. arXiv:1705.10257 (2017). * Pinnell, J., Rodríguez-Fajardo, V. & Forbes, A.

Single-step shaping of the orbital angular momentum spectrum of light. _Opt. Express_ 27, 28009–28021 (2019). Article  ADS  Google Scholar  * Mair, A., Vaziri, A., Weihs, G. & Zeilinger,

A. Entanglement of the orbital angular momentum states of photons. _Nature_ 412, 313–316 (2001). Article  ADS  CAS  Google Scholar  * Franke-Arnold, S., Barnett, S. M., Padgett, M. J. &

Allen, L. Two-photon entanglement of orbital angular momentum states. _Phys. Rev. A_ 65, 033823 (2002). Article  ADS  Google Scholar  * Vaziri, A., Weihs, G. & Zeilinger, A.

Experimental two-photon, three-dimensional entanglement for quantum communication. _Phys. Rev. Lett._ 89, 240401 (2002). Article  ADS  Google Scholar  * Nash, J. F. _et al._ Equilibrium

points in n-person games. _Proc. Natl. Acad. Sci. USA_ 36, 48–49 (1950). Article  ADS  MathSciNet  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported in part

by the CREST Project (JPMJCR17N2) funded by the Japan Science and Technology Agency, Grants-in-Aid for Scientific Research (JP20H00233) funded by the Japan Society for the Promotion of

Science, and CNRS-UTokyo Excellence Science Joint Research Program. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Mathematical Engineering and Information Physics, Faculty of

Engineering, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, 113-8656, Japan Takashi Amakasu, Nicolas Chauvet, Ryoichi Horisaki & Makoto Naruse * Department of Information

Physics and Computing, Graduate School of Information Science and Technology, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, 113-8656, Japan Nicolas Chauvet, Ryoichi Horisaki & 

Makoto Naruse * Université Grenoble Alpes, CNRS, Institut Néel, 38042, Grenoble, France Guillaume Bachelier & Serge Huant Authors * Takashi Amakasu View author publications You can also

search for this author inPubMed Google Scholar * Nicolas Chauvet View author publications You can also search for this author inPubMed Google Scholar * Guillaume Bachelier View author

publications You can also search for this author inPubMed Google Scholar * Serge Huant View author publications You can also search for this author inPubMed Google Scholar * Ryoichi Horisaki

View author publications You can also search for this author inPubMed Google Scholar * Makoto Naruse View author publications You can also search for this author inPubMed Google Scholar

CONTRIBUTIONS M.N., N.C., and G.B. directed the project. T.A., N.C., G.B., S.H., and M.N designed the system architecture. T.A. and N.C conducted physical modeling and numerical performance

evaluations. N.C., G.B., S.H., and R.H. examined technological constraints. All authors discussed the results. T.A., N.C., and M.N. wrote the manuscript. All authors reviewed the manuscript.

CORRESPONDING AUTHORS Correspondence to Takashi Amakasu or Makoto Naruse. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION

PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in

this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's

Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Amakasu, T., Chauvet, N., Bachelier, G. _et

al._ Conflict-free collective stochastic decision making by orbital angular momentum of photons through quantum interference. _Sci Rep_ 11, 21117 (2021).

https://doi.org/10.1038/s41598-021-00493-2 Download citation * Received: 02 July 2021 * Accepted: 12 October 2021 * Published: 26 October 2021 * DOI:

https://doi.org/10.1038/s41598-021-00493-2 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative