Reader TTS

ABSTRACT Dynamical properties of two-component mass-imbalanced few-fermion systems confined in a one-dimensional harmonic trap following a sudden quench of interactions are studied. It is

assumed that initially the system is prepared in the non-interacting ground state and then, after a sudden quench of interactions, the unitary evolution is governed by interacting many-body

Hamiltonian. By careful analysis of the evolution of the Loschmidt echo, density distributions of the components, and entanglement entropy between them, the role of mass imbalance and

particle number imbalance on the system’s evolution stability are investigated. All the quantities studied manifest a dramatic dependence on the number of heavy and lighter fermions in each

component at a given quench strength. The results may have implications for upcoming experiments on fermionic mixtures with a well-defined and small number of particles. SIMILAR CONTENT

BEING VIEWED BY OTHERS GENERATION AND DECAY OF HIGGS MODE IN A STRONGLY INTERACTING FERMI GAS Article Open access 12 July 2023 STATICS AND DYNAMICS OF NON-HERMITIAN MANY-BODY LOCALIZATION

Article Open access 13 March 2024 UNCONVENTIONAL PAIRING IN FEW-FERMION SYSTEMS AT FINITE TEMPERATURE Article Open access 19 October 2022 INTRODUCTION Detailed studies of non-equilibrium

dynamics of strongly correlated quantum systems have drawn tremendous attention over the last decades due to successful experimental realizations of different artificial many-body quantum

models with appropriately tailored ultracold quantum gases1,2,3,4. With these contemporary experimental setups it is possible to prepare microscopic systems with several degrees of

tunability, and thus, simulate different static and dynamical properties of quantum systems in a controlled manner. Importantly, these state-of-the-art experiments make it possible to change

external parameters on time scales that could be much faster or slower than the intrinsic microscopic time scales of the system. This possibility opens a route for fundamental studies of a

dynamical response to a whole spectrum of external disturbances4,5,6,7,8,9,10. Experiments involving ultracold atoms allow to realize of two-component many-body quantum systems with flavors

obeying different quantum statistics, _e.g._, Bose-Bose11,12,13, Bose-Fermi14,15,16,17,18,19,20, and Fermi-Fermi21,22,23,24,25 mixtures. It is worth noting that also multi-component systems

are currently under experimental control26, 27. Additionally, these high-precision experiments also offer great tunability of the number of particles in each component and the

inter-component interaction strength between the species28,29,30. This reopened new windows for theoretical investigations of such systems (for review see31,32,33,34,35). Having all these

experimental and theoretical scenarios in mind, here we focus on quench dynamics of two-component mass-imbalanced fermionic systems in the regime of a small number of particles. In this way,

we try to bridge studies on large ultra-cold mass-imbalanced fermionic mixtures with recent experiments on systems containing several fermions of the same mass in quasi-one-dimensional

confinement29. Specifically, we investigate the sudden quench dynamics of such systems prepared initially in the noninteracting many-body ground state. We assume that interactions are

suddenly switched on and we study the nonequilibrium effect of this sudden perturbation on the system’s dynamical properties. As a figure of merit, we use the Loschmidt echo36, 37 as an

adequate indicator for quantifying such a nonequilibrium effect. The Loschmidt echo has been used as an important and very useful tool in many physical out-of-equilibrium dynamical problems.

This includes, studies of criticality in spin chains38,39,40, dynamical quantum phase transition in one-dimensional models41, 42, finite temperature quantum phase transitions43,

orthogonality catastrophe in Fermi polaron system44, Bose polaron in small quenched quantum gas system36, and in many others. Further, we support the conclusions obtained from the Loschmidt

echo by examining the evolution of the particle density distributions and the inter-component correlations. Particularly, the effect of the mass imbalance and the particle imbalance are

systematically investigated for different systems with up to six particles. To obtain numerically credible results, to find the time-evolved state of the system, we use a combination of

methods based on the exact diagonalization of the many-body Hamiltonian and the decomposition of the unitary evolution operator into the Chebyshev polynomials (so-called, the Chebyshev

evolution technique)45, 46. In this way, we can obtain well-converged results for short-time as well as long-time dynamics. Here we want to emphasize that interaction-driven quench processes

have also been studied previously for two-component mixtures of different statistics, particularly systems consisting of few particles36, 47,48,49,50. For instance, the authors considered a

few-body system consisting of two bosons and a single impurity atom of equal mass. They started with an initial state in which the two bosons are in the Tonks-Girardeau interacting limit

and then study the evolution of the Loschmidt echo at different inter-component interaction strengths. This study merely implies that even a small mixture of quantum particles can witness

complete orthogonality between two states evolved by the Hamiltonians before and after a sudden quench. Similarly, various dynamical properties for interaction quench-driven processes in

systems with two bosonic impurities immersed in a Fermi sea for a mass-balanced scenario were recently studied51. THE SYSTEM STUDIED In our present model, we focus on a few-body system

containing two-component mass-imbalanced spin-polarized fermions confined in a one-dimensional harmonic trap. Particles from opposite components interact with each other by short-range

contact forces through a low-energy (_s_-wave) scattering channel. The many-body Hamiltonian representing this mesoscopic system can then be given by $$\begin{aligned} \hat{\mathscr {H}}(g)

= \sum _{\sigma } \int \!\!{\textrm{d}}x\,{{\hat{\Psi }}}^{\dagger }_{\sigma }(x) H_{\sigma } {{\hat{\Psi }}}_{\sigma }(x) + g \int {\textrm{d}}x\,{\hat{\Psi} }^{\dagger }_{\uparrow }(x)

{{\hat{\Psi }}}^{\dagger }_{\downarrow }(x) {{\hat{\Psi }}}_{\downarrow }(x) {\hat{\Psi}}_{\uparrow }(x), \end{aligned}$$ (1) where \({\hat{\Psi }}_{\sigma }(x)\) denotes the field operator

annihilating fermion from a component \(\sigma \in \{\downarrow ,\uparrow \}\) at a spatial position _x_, while _g_ is the effective short-range interaction strength between components52.

\(H_\sigma\) represents the single-particle Hamiltonian for the component \(\sigma\) and it is justified in the following. It is straightforward to check that the Hamiltonian (1) does

commute with the particle number operators for each component, \(\left[ \hat{\mathscr{H}}(g), \hat{N}_\sigma \right] = 0\), where \(\hat{N}_\sigma =\int {\textrm{d}}x{\hat{\Psi }}_{\sigma

}^\dagger (x){\hat{\Psi }}_{\sigma }(x)\). Thus, its properties can be explored in the subspaces of fixed numbers of particles \(N_\uparrow\) and \(N_\downarrow\). For convenience, in our

work, we use the notation \([\![N_\uparrow ,N_\downarrow ]\!]\) to specify the number of particles in each component, by \(N=N_\uparrow +N_\downarrow\) we indicate the total number of

particles, and we write \(\hat{\mathscr{H}}_0\) for the non-interacting Hamiltonian \(\left. \hat{\mathscr{H}}(g)\right| _{g=0}\). We focus on mixtures of fermions having different masses

which currently are under investigation in various experimental laboratories. In particular, we study quench dynamics with our few-body setup for mass ratios \(\mu \in \{1.8, 2.2, 4.0, 4.2,

6.7\}\) which correspond respectively to the following ultracold atomic mixtures: \(^{161}\)Dy-\(^{87}\)Sr, \(^{87}\)Sr-\(^{40}\)K, \(^{161}\)Dy-\(^{40}\)K, \(^{167}\)Er-\(^{40}\)K,

\(^{40}\)K-\(^{6}\)Li. In our theoretical model, we assume that both fermionic components experience the same one-dimensional trapping potential. This commensurate potential approximation

can also be realized in experiments by properly tuning the width and intensity of the applied laser field. Of course, analogous calculations can be carried out for systems with

component-dependent potentials. However, in the present study, we mostly focus on the effect of mass and particle imbalance on the dynamical properties of the system, so our approximated

model can capture most of the relevant physics. With the above approximation, the single-particle Hamiltonian takes the following form $$\begin{aligned} H_\sigma = -\frac{\hslash

^2}{2m_\sigma }\frac{{\textrm{d}}^2}{{\textrm{d}}x^2}+\frac{m_\sigma \omega ^2}{2}x^2. \end{aligned}$$ (2) By expressing all the physical quantities in the natural units of the harmonic

oscillator related to one of the flavors (here we choose a lighter spin-down component) the single-particle Hamiltonians can be simplified as $$\begin{aligned} H_{\downarrow }&=

-\frac{1}{2}\frac{{\textrm{d}}^2}{{\textrm{d}}x^2} +\frac{1}{2}x^2, ~~~~ H_{\uparrow }&= -\frac{1}{2\mu }\frac{{\textrm{d}}^2}{{\textrm{d}}x^2} +\frac{\mu }{2}x^2, \end{aligned}$$ (3)

where \(\mu =m_\uparrow /m_\downarrow\) is the mass ratio between two fermionic flavors. Obviously, analytical expressions for all eigenstates of these differential operators are well-known

and given by $$\begin{aligned} \phi ^{\downarrow }_n (x)&= \left( 2^n n! \sqrt{\pi }\right) ^{-1/2} \textrm{H}_{n}(x) e^{-x^2/2}, \end{aligned}$$ (4a) $$\begin{aligned} \phi ^{\uparrow

}_n (x)&= \left( 2^n n! \sqrt{\pi /\mu }\right) ^{-1/2} \textrm{H}_n(\sqrt{\mu }x) e^{-\mu x^2/2}, \end{aligned}$$ (4b) where \(\textrm{H}_n (x)\) is the _n_-th order Hermite polynomial.

In terms of these single-particle orbitals one can now introduce corresponding annihilation operators \(\hat{a}_n\) and \(\hat{b}_n\) (respectively for lighter and heavier component

particles) to expand the field operators as $$\begin{aligned} {\hat{\Psi }}_{\downarrow }(x) = \sum _n \hat{a}_{n} \phi ^{\downarrow }_{n}(x), \qquad {\hat{\Psi }}_{\uparrow }(x) = \sum _n

\hat{b}_{n} \phi ^{\uparrow }_{n}(x), \end{aligned}$$ (5) and write the original Hamiltonian (1) as $$\begin{aligned} \hat{\mathscr {H}}(g) = \sum _i \varepsilon _{i}\left( \hat{a}^{\dagger

}_{i}\hat{a}_{i} + \hat{b}^{\dagger }_{i}\hat{b}_{i}\right) + g\sum _{ijkl} U_{ijkl} \hat{a}^{\dagger }_{i}\hat{b}^{\dagger }_{j}\hat{b}_{k}\hat{a}_{l} \end{aligned}$$ (6) Note that in the

case studied the single-particle energy \(\varepsilon _i=i+1/2\) is the same for both components. The two-body interaction coefficients are given by the general formula $$\begin{aligned}

U_{ijkl} = \int {\textrm{d}}x \ \phi ^{\uparrow *}_{i}(x) \ \phi ^{\downarrow *}_{j}(x) \ \phi ^{\downarrow }_{k}(x) \ \phi ^{\uparrow }_{l}(x). \end{aligned}$$ (7) and in the case of

harmonic oscillator confinement, they can be calculated analytically53. In this way one may represent the original Hamiltonian (1) as a matrix with matrix elements of the generic form

\(\mathscr{H}_{ij}=\langle \mathscr{F}_i|\hat{\mathscr{H}}(g)|\mathscr{F}_j\rangle\), where the set \(\{|\mathscr{F}_i\rangle \}\) contains all possible Fock states representing

non-interacting Hamiltonian \(\mathscr{H}_0\). In principle, this approach allows one to perform all calculations in this representation. In practice, however, some reasonable cutoff of the

Fock basis is needed due to a finite numerical resources used53,54,55,56. In our work, we focus on the dynamical properties of the system after a sudden quench of interactions. We assume

that initially the system is prepared in the non-interacting ground state of the system \(|\texttt{ini}\rangle\) with eigenenergy \(E_\texttt{ini}=(N_\uparrow ^2+N_\downarrow ^2)/2\). For

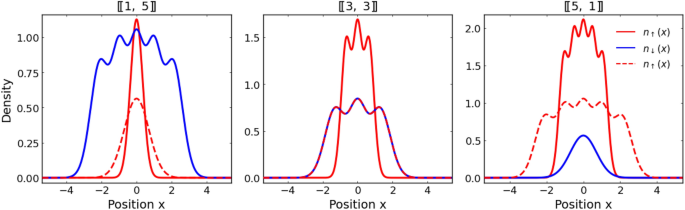
convenience of further discussion in Fig. 1 we present initial density distribution \(n_{\sigma }(x) = \langle \texttt{ini}|{\hat{\Psi }}_{\sigma }^{\dagger }(x) {\hat{\Psi }}_{\sigma }(x)

|\texttt{ini}\rangle\) of different components for exemplary case of \(N=6\) particles differently distributed between components. Then, at \(t=0\), the interaction strength is suddenly

changed to _g_ and the system starts to evolve according to the Hamiltonian \(\hat{\mathscr{H}}(g)\). In general, the most straightforward method of finding the time-evolved state for short

times is to solve time-dependent Schrödinger equation, \(i\partial _t|\Psi (t)\rangle = \hat{\mathscr{H}}(g)|\Psi (t)\rangle\), with the standard fourth-order Runge-Kutta algorithm. If the

long-time behavior of the system is considered, then one first needs to perform exact diagonalization of the target Hamiltonian \(\hat{\mathscr{H}}(g)\). Then the time-evolved state can be

obtained as an appropriate superposition of time-evolved eigenstates \(\{|\Upsilon _n \rangle \}\) having corresponding eigenenergies \(E_n\) $$\begin{aligned} |\Psi (t)\rangle = \sum _n

\langle \Upsilon _n|\texttt{ini}\rangle \,\textrm{e}^{-iE_nt}\,|\Upsilon _n\rangle \end{aligned}$$ (8) In practice, these two straightforward methods are however feasible only for relatively

small systems57 or for large systems close to the non-interacting limit. It comes from the fact that the size of the Hilbert subspace of states which have a relevant contribution to the

dynamics strongly depends on interaction strength _g_ and also grows exponentially with the number of particles \([\![N_\uparrow ,N_\downarrow ]\!]\). Therefore, to tackle larger systems we

employ the Chebyshev time evolution technique, which has been successfully applied to many physical problems concerning time dynamics58, 59. We found that the Chebyshev evolution technique

is a quite remarkable approach to producing short-time and long-time dynamical behavior. The Chebyshev time-evolution technique is based essentially on expressing the unitary evolution

operator \(U(t) = \textrm{e}^{-i \hat{\mathscr{H}}(g) t}\) in terms of Chebyshev polynomials \(\textrm{T}_k(x)\). The technical details of the method and relevant derivations can be found

in59,60,61. In the following, we present only working steps in this framework. The formal form of the expansion reads $$\begin{aligned} U(t) = e^{-i\beta t} \left( c_0 + 2\sum ^{\mathscr

{D}}_{k=1} c_k(t)\,\textrm{T}_k ({\hat{\mathscr{R}}}) \right) , \end{aligned}$$ (9) where \(\hat{\mathscr{R}}=\left[ \hat{\mathscr{H}}(g) - \beta \right] /\alpha\) is the so-called rescaled

Hamiltonian. Simply, this is the Hamiltonian shifted and rescaled in such a way that the relevant part of its spectrum is spanned between \([-1, 1]\). The scaling parameters \(\alpha\) and

\(\beta\) are determined by extreme eigenvalues (\(E_\text{min}\) and \(E_\text{max}\), respectively) of the original Hamiltonian \(\hat{\mathscr{H}}\) and they are defined as \(\alpha =

(E_\text{max}-E_\text{min})/2\) and \(\beta = (E_\text{max} + E_\text{min})/2\). In contrast to the standard method for time evolution (8), application of the Chebyshev time-evolution

technique does not require knowledge of all eigenstates and eigenvalues of the many-body Hamiltonian, but only extremal eigenenergies \(E_\text{min}\) and \(E_\text{max}\). Since they can be

found quite quickly with a few iterations of the standard Lanczos algorithm, the method becomes feasible also for relatively large Hamiltonian matrices. Moreover, the accuracy of this

approach is controlled solely by the order of the Chebyshev polynomial \(\mathscr D\). It is set at a reasonably large value to get a well-converged dynamical behavior. At this point, one

should remember that the full many-body Hamiltonian (1) is in principle not bounded from above. Therefore, maximal energy \(E_\text{max}\) is not well-defined. However in practice, due to a

specific cut-off of the Fock space used to represent the Hamiltonian as a finite matrix, the largest eigenvalue \(E_\text{max}\) exists and it is directly related to this cut-off. In our

calculations, the cut-off is determined by the number of single-particle orbitals used in the decomposition (5). For systems with a single impurity and two, three, four, and five particles

in the majority component we take respectively 20, 20, 18, and 15 single-particle orbitals. For the balanced systems with two, four, and six particles we take 25, 18, and 12 orbitals,

respectively. Note also that extremal energies \(E_\text{min}\) and \(E_\text{max}\) is not unique for all systems since they depend also on the mass ratio \(\mu\). We checked that further

increasing the number of orbitals affects the dynamics only minutely. The expansion coefficients \(c_k(t)\) in the decomposition (9) are given by \(c_k = (-i)^k \textrm{J}_k(\alpha t)\),

where \(\textrm{J}_k(\tau )\) denotes the _k_-th order spherical Bessel function of the first kind. The maximum order of the Chebyshev polynomial is determined by the dimension of the

cropped Hilbert space \(\mathscr {D}\). In practice, however, due to a superexponential decay of Bessel functions \(\textrm{J}_k(\tau )\sim (\tau /k)^k\), one can truncate the summation on a

much smaller cutoff \({\mathscr{D}}_{\textrm{C}}\) after achieving the desired accuracy. For example, for \(\mathscr {D} = 48400\) (corresponding to \(N_\uparrow =N_\downarrow =3\) with

\(\mathscr{K}=12\) single-particle orbitals for each component), we find that \(\mathscr{D}_C \sim 400\) is sufficient to ensure numerical convergence of the results for the whole time

domain considered in our work. LOSCHMIDT ECHO One of the most relevant figures of merit for capturing the nonequilibrium effect of a quenching process is the dynamical Loschmidt echo

\(\mathscr {L}(t)\) commonly defined as36, 37 $$\begin{aligned} \mathscr {L}(t) = |\langle \texttt{ini}| \textrm{e}^{i \hat{\mathscr{H}}_0 t}|\Psi (t) \rangle |^2 = |\langle \texttt{ini}|

\textrm{e}^{i \hat{\mathscr{H}}_0 t} \textrm{e}^{-i \hat{\mathscr{H}}(g) t}|\texttt{ini} \rangle |^2. \end{aligned}$$ (10) From the above formulation, it is clear that \(\mathscr {L}(t)\)

essentially quantifies differences between the initial state \(|\texttt{ini}\rangle\) unitary time-evolved by the Hamiltonian \(\hat{\mathscr{H}}(g)\) and by the non-interacting Hamiltonian

\(\hat{\mathscr{H}}_0\). Thus, whenever the echo becomes close to one, the time-evolved state of an interacting system is well-approximated by the state obtained with a trivial evolution of

the non-interacting system with non-interacting Hamiltonian \(\hat{\mathscr{H}}_0\). Using eigenstates \(\{|\Upsilon _n \rangle \}\) of the final Hamiltonian \(\hat{\mathscr{H}}(g)\) and

corresponding eigenenergies \(E_n\), one can further simplify \(\mathscr {L}(t)\) as $$\begin{aligned} \mathscr {L}(t) = \left| \sum _n \textrm{e}^{i(E_n - E_\texttt{ini})t} |\langle

\texttt{ini} |\Upsilon _n \rangle |^2 \right| ^2. \end{aligned}$$ (11) This reformulation gives another interpretation of the Loschmidt echo as a cumulative interference of interacting

eigenstates contributing to the initial state. However, calculation of \(\mathscr {L}(t)\) with this definition is in practice not feasible for larger systems since it requires precise

knowledge of the full eigenspectrum of interacting Hamiltonian \(\hat{\mathscr{H}}(g)\). As such, it is suitable rather for smaller system sizes with a reasonable number of single-particle

orbitals. Let us first discuss the dynamical behavior of the Loschmidt echo for different mass mixtures containing an imbalanced number of particles. In the simplest case, we consider a

single impurity (lighter or heavier) immersed in a few-fermion bath of the opposite component. In Fig. 2, we present the time dependence of \(\mathscr{L}(t)\) for two different interaction

strengths _g_ and three different mass ratios \(\mu\). Different blue and red shaded lines correspond to systems with heavier and lighter impurity and a different number of majority

particles (_i.e._, systems with \([\![1,N_\downarrow ]\!]\) and \([\![N_\uparrow ,1]\!]\) particles, respectively). As a general observation, we notice that whenever interactions between the

lighter impurity with a heavy fermionic bath are switched on the Loschmidt echo decays quite faster than in the opposite situation with a single heavy impurity immersed in a lighter medium.

It is also much more sensitive to the value of mass ratio and even for relatively weak interactions it may rapidly drop to zero. This suggests that small polaron systems with light impurity

are very sensitive to interactions and evolve significantly different than their non-interacting counterparts. In contrast, systems with heavy impurity typically are very robust to

interactions and also to the mass difference. It is clear, that independently of the mass ratio, all blue lines behave very similarly. Thus, an increasing number of particles in the majority

component has the opposite impact on the Loschmidt echo. In contrast, for lighter impurity (system with \([\![N_\uparrow ,1]\!]\) particles), when the number of particles in the bath is

increased, the dynamics of the system drives away more deeply from the non-interacting case. The main reason standing behind such different resistivity of light and heavy impurity comes from

the essential difference of initial density distribution profiles (see Fig. 1). In the case of heavy impurity, the increasing number of lighter particles almost does not affect the

interaction energy (proportional to the overlap of single-particle density profiles). Thus it changes the behavior of the system only marginally. The situation is significantly different

when light impurity is considered. Then, the density overlap changes significantly when the number of heavy particles is increased. Provided that the mass ratio is sufficiently large, the

density distribution of the light particle is always spread over the entire heavy bath. An intermediate behavior of \(\mathscr {L}(t)\) is clearly visible for systems with a balanced number

of particles, \([\![N/2,N/2]\!]\) (see Fig. 3). Along with the increasing number of particles, interactions, and/or mass ratio, the system drives away from the noninteracting dynamics and

its periodic revivals become less accurate. Only a fully integrable case with \([\![1,1]\!]\) particles manifests relative stability and resistance to the model’s parameter change. For

completeness of this analysis, in Fig. 4 we expose an impact of the mass difference on the dynamical properties of the system with \(N=6\) particles differently distributed among components.

The detailed inspection and comparison show a general trend that increasing of mass ratio leads to a stronger and quicker departure from the non-interacting dynamics. This effect is further

enhanced when the number of heavier atoms increases. Indeed, the time evolution of the Loschmidt echo for the system with only one heavy atom (left column in Fig. 4) is poorly sensitive to

the mass ratio \(\mu\). Contrary, in the case of a system with a single lighter impurity (right column in Fig. 4) the echo quickly drops close to zero for a large enough mass ratio even for

small interaction strengths. Further, to understand the role of the number of particles and particle imbalance with respect quench strength, in Fig. 5 we present the full dynamical picture

of the Loschmidt echo for the whole range of interactions after the quench for systems with \(N=4\), 5, and 6 particles and fixed mass ratio \(\mu =4.0\) (dysprosium-potassium mixture). It

is clear that the most stable and regular pattern is obtained for systems with only one heavy impurity \([\![1,N_\downarrow ]\!]\). In these cases revivals (\(\mathscr{L}\approx 1\)) appear

periodically for any interaction strength and every number of lighter particles. Situation changes, when the number of heavy particles increases. For example, for balanced systems

\([\![N/2,N/2]\!]\) regular pattern is present only for smaller interactions and a smaller number of particles. In the case of an extreme case, when only one light particle is present in the

system (_i.e._ the system contains \([\![N_\uparrow ,1]\!]\) particles), the Loschmidt echo pattern quickly become irregular, and in fact unpredictable. DENSITY PROFILE AFTER QUENCH The

dynamical behavior of the system after the quench of interactions is reflected in many different, directly measurable quantities. One of them is the single-particle density profile which is

defined as $$\begin{aligned} n_{\sigma } (x,t) = \langle \Psi (t)|{\hat{\Psi }}_{\sigma }^{\dagger }(x) {\hat{\Psi }}_{\sigma }(x) |\Psi (t) \rangle . \end{aligned}$$ (12) The time evolution

of these densities for both components is presented in Fig. 6 for differently balanced systems containing \(N=6\) particles. For clarity, we present calculations only for one selected mass

ratio \(\mu = 4.0\) (dysprosium-potassium mixture) and three different interaction strengths. Nevertheless, we checked that calculations made for other parameters lead to analogous

conclusions. For an imbalanced system with one heavy impurity \([\![1,5]\!]\), we notice that the spatial extent of the impurity is mildly affected by the interactions and the profile stays

highly Gaussian around the harmonic center. Only for strong enough interactions, some sort of fragmentation of the density occurs and some deviations from the Gaussian shape start to build

up. Subsequently, the effect of the heavy particle on the lighter medium is also not significant, leading to an almost stationary density distribution of the majority component overall range

of interactions studied. Such a mild effect of interaction quench on the density profile of both components is fully compatible with slow and regular changes of the Loschmidt echo

\(\mathscr {L}(t)\) (compare with Fig. 2). On the contrary, in the case of a system containing a majority of heavy particles and a single light impurity \([\![5,1]\!]\), the effect of the

sudden quench process is substantial. Time evolution of the density profile of the heavy component \(n_\uparrow (x,t)\) is strongly affected and quickly become unpredictable. The density

distribution of light impurity \(n_\downarrow (x,t)\) is affected even much stronger and smeared over the entire area in which the system is located. Exactly as was observed in the case of

Loschmidt echo, the behavior of a fully balanced system with \([\![3,3]\!]\) particles is intermediate when compared to the two extreme cases discussed. Again, these different behaviors of

the system for a different distribution of particles between components can be viewed as a consequence of substantially different density distributions at the initial moment. It is worth

adding, that similar evolution of density pattern was recently found in the case of a spinor impurity atom immersed in a BEC of spinless bosons62. By comparing time evolutions of the

Loschmidt echo \(\mathscr {L}(t)\) and the density distributions \(n_\sigma (x,t)\) one can observe almost ideal coincidence correspondence of the revival moments for these quantities. It is

also evident that whenever the impurity atom comes close to the center of the trap, the value of the echo \(\mathscr {L}(t)\) increases. Contrary, it is diminished when the impurity moves

away from the center. Moreover, the density profiles for the balanced system show a symmetric behavior around the trap center at any value of interaction quench. It is interesting to note

that a very similar behavior of the density profile was recently observed for a system containing two bosons and one impurity atom36. FORMATION OF INTER-COMPONENT CORRELATIONS A

complimentary look at the effect of sudden quench on the dynamical properties of the system can be obtained by calculating the time evolution of inter-component correlations. They can be

quantified through the von Neumann entropy given by36 $$S(t) = - {\text{Tr}}\left[ {\hat{\rho }_{\sigma } (t)\ln \hat{\rho }_{\sigma } (t)} \right]$$ (13) where \(\hat{\rho }_{\sigma }(t)\)

is the temporal reduced density matrix of the \(\sigma\)-component calculated by tracing-out opposite component \(\sigma '\) from the operator projecting to the temporal state \(|\Psi

(t)\rangle\), _i.e._, \(\hat{\rho }_{\sigma }(t)=\textrm{Tr}_{\sigma '} \left[ |\Psi (t)\rangle \langle \Psi (t)|\right]\). It is a matter of fact that the value of the entropy (13)

does not depend on the choice of the component \(\sigma\) used for calculations. However, from the computational point of view, tracing out a larger component is usually much more efficient.

Since both components are distinguishable and initially the system is prepared in the product state \(|\texttt{ini}\rangle\), just after the quench the entropy \(S(0) = 0\). Then, due to

inter-component interactions, entropy starts to increase signaling the appearance of inter-component correlations. Depending on interactions and the number of particles, the formation of

correlations has different intensities. As suspected, due to a difference in initial density distributions, inter-particle correlations are built much faster in systems when the number of

heavy particles is larger. In Fig. 7 we present detailed results obtained for systems with \(N=6\) particles and two different values of interactions. In addition, in Fig. 8 we present

complete results for the same systems obtained in a whole range of interactions. In this way, it is possible to compare entropy production with the evolution of the Loschmidt echo (bottom

row in Fig. 5). When relating the temporal evolution of entropy to the characteristic time of a harmonic oscillator, we see that in each case considered, it increases rapidly at the

beginning of the evolution, and then stabilizes at a certain level long before the end of the first period. The evolution shows characteristic periodic peaks. However, they are weaker as the

interactions become stronger and the mass ratio larger. This is fully consistent with the Loschmidt echo revivals shown earlier. It is also clear that entanglement entropy increases faster

for systems with a larger mass ratio \(\mu\) (it is particularly visible when a strongly imbalanced system with light impurity is considered). This is also in agreement with previous

results. Let us now finally compare the evolution of the inter-component correlations with the dynamics of spatial distributions of the components. As argued above, for the system with

\([\![1,5]\!]\) particles the spatial extent of the heavy impurity is mildly affected by interactions with the lighter environment. Thus, the two components are probably less correlated and

subsequently, the value of entropy _S_(_t_) saturates on a relatively small level. In contrast, for the system with \([\![5,1]\!]\) particles the density profile of the lighter impurity is

highly influenced by the presence of a heavy bath implying strong correlations between components. In consequence, entanglement entropy approaches higher levels. This comparison proves that

mutual influences of the components forced by interactions have a quantum nature and cannot be explained by any classical picture of interacting fluids. CONCLUSIONS We have investigated the

dynamical properties of a system consisting of a few mass-imbalanced harmonically trapped fermions after a sudden quench of interactions. Comparing the dynamical behavior of the Loschmidt

echo \(\mathscr {L}(t)\) we show increasing orthogonality to the non-interacting evolution along with increasing mass imbalance and interactions. As suspected, stronger interactions are

directly responsible for the faster creation of correlations between particles. This is reflected in the faster production of entanglement and its saturation on a larger level. Consequently,

the temporal state of the system faster departs from the time-evolved state for non-interacting cases (reflected by the quick change of the Loschmidt echo). Our less intuitive finding is

that the orthogonality strongly depends on the number of particles in the heavy and light components. In particular, a strong enhancement of the echo’s decay is observed by increasing the

quench strength for the systems with larger heavy components. In these systems, the long-time dynamics become very chaotic, especially for large mass imbalances. A system with a small number

of heavy fermions manifests quite strong stability, independently of the mass ratio between particles from opposite components. Intermediate behavior is observed for systems with a balanced

number of particles. We attribute this rather significant difference in the behavior of systems with different imbalances mainly to differences in the density distributions of the

individual components. These differences significantly change the overlap integrals, which are related to the interaction energy. The behavior of the Loschmidt echo is further supported by

examining the temporal density distributions and inter-component correlations. We find that for systems with a single heavy impurity the interaction quench (even strong) does not change

significantly their spatial distributions. In contrast, for systems with light impurity, the temporal density distributions become highly affected by surrounding heavier medium. As a result,

also the spatial distribution of the heavier component is significantly enlarged, especially for stronger quenches. Again, for the balanced-particle scenario, the density profiles become

diffusive with the increase of the inter-component coupling. However, this spreading occurs quite smoothly maintaining a periodic trend for both flavors even at the strong quench. With these

results in hand, one can explore further different directions of such mass-imbalanced systems. Here, we give some of the possible future studies that can be worth looking at. As we found

the physical properties of the polaron highly depend on the nature of the impurity atom (heavier/lighter) compared to the medium and quantum statistics. Thus, it would be interesting to

explore the dynamical orthogonality of small polaron systems in experiments for bosonic particles as well as for flavors having particles of different mass. As an extension, one can study

the Loschmidt echo dynamics of such systems for a more general initial state. For instance, considering scenarios in which the system is initially prepared in some superposition of

non-interacting states or even in a thermal mixed state may be very instructive and relevant, also from an experimental perspective. One can also rigorously study the effect of an increasing

number of impurity atoms (multi-polaron systems) on orthogonality and consequently capture dynamical effects forced by quantum statistics. It is also worth investigating the quasiparticle

excitations properties through radio-frequency spectroscopy or analyzing the spectral function from \(\mathscr {L}(t)\) of the present confined system. Another useful direction is to unravel

the few to many-body crossover point concerning the size of the bath component both for \([\![1,N_{\downarrow }]\!]\) and \([\![N_{\uparrow },1]\!]\) scenario. Finally, our present study

can be a starting point for investigating the dynamical behavior of the impurity subjected to a quantum quench process in a one-dimensional optical lattice focusing on a mass-imbalanced

two-component fermionic system with harmonic confinement. Such an optical lattice system can provide a platform to understand the polaron physics in an extended system on a general ground

compared to its equal mass counterpart. DATA AVAILABILITY All data generated or analyzed during this study are available from the corresponding author upon reasonable request. CHANGE HISTORY

* _ 07 FEBRUARY 2023 A Correction to this paper has been published: https://doi.org/10.1038/s41598-023-29085-y _ REFERENCES * Bloch, I., Dalibard, J. & Zwerger, W. Many-body physics

with ultracold gases. _Rev. Mod. Phys._ 80, 885–964. https://doi.org/10.1103/RevModPhys.80.885 (2008). Article  ADS  CAS  Google Scholar  * Trotzky, S. _et al._ Probing the relaxation

towards equilibrium in an isolated strongly correlated one-dimensional Bose gas. _Nat. Phys._ 8, 325–330. https://doi.org/10.1038/nphys2232 (2012). Article  CAS  Google Scholar  * Georgescu,

I. M., Ashhab, S. & Nori, F. Quantum simulation. _Rev. Mod. Phys._ 86, 153–185. https://doi.org/10.1103/RevModPhys.86.153 (2014). Article  ADS  Google Scholar  * Polkovnikov, A.,

Sengupta, K., Silva, A. & Vengalattore, M. Colloquium: Nonequilibrium dynamics of closed interacting quantum systems. _Rev. Mod. Phys._ 83, 863–883.

https://doi.org/10.1103/RevModPhys.83.863 (2011). Article  ADS  Google Scholar  * Pustilnik, M., Khodas, M., Kamenev, A. & Glazman, L. I. Dynamic response of one-dimensional interacting

fermions. _Phys. Rev. Lett._ 96, 196405. https://doi.org/10.1103/PhysRevLett.96.196405 (2006). Article  ADS  CAS  Google Scholar  * Nascimbène, S. _et al._ Collective oscillations of an

imbalanced fermi gas: Axial compression modes and polaron effective mass. _Phys. Rev. Lett._ 103, 170402. https://doi.org/10.1103/PhysRevLett.103.170402 (2009). Article  ADS  CAS  Google

Scholar  * Pereira, R. G., White, S. R. & Affleck, I. Spectral function of spinless fermions on a one-dimensional lattice. _Phys. Rev. B_ 79, 165113.

https://doi.org/10.1103/PhysRevB.79.165113 (2009). Article  ADS  CAS  Google Scholar  * Sindona, A., Goold, J., Gullo, N. L. & Plastina, F. Statistics of the work distribution for a

quenched fermi gas. _New J. Phys._ 16, 045013. https://doi.org/10.1088/1367-2630/16/4/045013 (2014). Article  ADS  Google Scholar  * Bhattacharya, A., Das, S. & Biswas, S. Particle

scattering by harmonically trapped Bose and fermi gases. _J. Phys. B At. Mol. Opt. Phys._ 51, 075301. https://doi.org/10.1088/1361-6455/aaafb4 (2018). Article  ADS  CAS  Google Scholar  *

Das, S. Particle scattering by harmonically trapped quantum gases in an artificial magnetic field. _Physica B: Condensed Matter_ 635, 413833. https://doi.org/10.1016/j.physb.2022.413833

(2022). Article  CAS  Google Scholar  * Schulze, T. A. _et al._ Feshbach spectroscopy and dual-species Bose-Einstein condensation of \(^{23}\rm Na\)–\(^{39}\rm K\) mixtures. _Phys. Rev. A_

97, 023623. https://doi.org/10.1103/PhysRevA.97.023623 (2018). Article  ADS  CAS  Google Scholar  * Catani, J., De Sarlo, L., Barontini, G., Minardi, F. & Inguscio, M. Degenerate

Bose-Bose mixture in a three-dimensional optical lattice. _Phys. Rev. A_ 77, 011603. https://doi.org/10.1103/PhysRevA.77.011603 (2008). Article  ADS  CAS  Google Scholar  * Thalhammer, G.

_et al._ Double species Bose-Einstein condensate with tunable interspecies interactions. _Phys. Rev. Lett._ 100, 210402. https://doi.org/10.1103/PhysRevLett.100.210402 (2008). Article  ADS 

CAS  Google Scholar  * Onofrio, R. Cooling and thermometry of atomic fermi gases. _Phys. Uspekhi_ 59, 1129–1153. https://doi.org/10.3367/ufne.2016.07.037873 (2016). Article  ADS  CAS  Google

Scholar  * Hadzibabic, Z. _et al._ Two-species mixture of quantum degenerate Bose and Fermi gases. _Phys. Rev. Lett._ 88, 160401. https://doi.org/10.1103/PhysRevLett.88.160401 (2002).

Article  ADS  CAS  Google Scholar  * Günter, K., Stöferle, T., Moritz, H., Köhl, M. & Esslinger, T. Bose-Fermi mixtures in a three-dimensional optical lattice. _Phys. Rev. Lett._ 96,

180402. https://doi.org/10.1103/PhysRevLett.96.180402 (2006). Article  ADS  CAS  Google Scholar  * Best, T. _et al._ Role of interactions in \({^{87}}{\rm Rb}--{^{40}}\) K Bose-Fermi

mixtures in a 3d optical lattice. _Phys. Rev. Lett._ 102, 030408. https://doi.org/10.1103/PhysRevLett.102.030408 (2009). Article  ADS  CAS  Google Scholar  * Wu, C.-H., Santiago, I., Park,

J. W., Ahmadi, P. & Zwierlein, M. W. Strongly interacting isotopic Bose-Fermi mixture immersed in a fermi sea. _Phys. Rev. A_ 84, 011601. https://doi.org/10.1103/PhysRevA.84.011601

(2011). Article  ADS  CAS  Google Scholar  * Tung, S.-K., Jiménez-García, K., Johansen, J., Parker, C. V. & Chin, C. Geometric scaling of efimov states in a \(^{6}\rm Li\)–\(^{133}\rm

Cs\) mixture. _Phys. Rev. Lett._ 113, 240402. https://doi.org/10.1103/PhysRevLett.113.240402 (2014). Article  ADS  CAS  Google Scholar  * Lous, R. S. _et al._ Probing the interface of a

phase-separated state in a repulsive Bose-Fermi mixture. _Phys. Rev. Lett._ 120, 243403. https://doi.org/10.1103/PhysRevLett.120.243403 (2018). Article  ADS  CAS  Google Scholar  * Wille, E.

_et al._ Exploring an ultracold Fermi-Fermi mixture: Interspecies Feshbach resonances and scattering properties of \({^{6}}{\rm Li}\) and \({^{40}}{\rm K}\). _Phys. Rev. Lett._ 100, 053201.

https://doi.org/10.1103/PhysRevLett.100.053201 (2008). Article  ADS  CAS  Google Scholar  * Cetina, M. _et al._ Decoherence of impurities in a Fermi sea of ultracold atoms. _Phys. Rev.

Lett._ 115, 135302. https://doi.org/10.1103/PhysRevLett.115.135302 (2015). Article  ADS  CAS  Google Scholar  * Ravensbergen, C. _et al._ Production of a degenerate Fermi-Fermi mixture of

dysprosium and potassium atoms. _Phys. Rev. A_ 98, 063624. https://doi.org/10.1103/PhysRevA.98.063624 (2018). Article  ADS  CAS  Google Scholar  * Tiecke, T. G. _et al._ Broad Feshbach

resonance in the \({^{6}}{\rm Li}\)–\({^{40}}\) K mixture. _Phys. Rev. Lett._ 104, 053202. https://doi.org/10.1103/PhysRevLett.104.053202 (2010). Article  ADS  CAS  Google Scholar  * Cetina,

M. _et al._ Ultrafast many-body interferometry of impurities coupled to a Fermi sea. _Science_ 354, 96–99. https://doi.org/10.1126/science.aaf5134 (2016). Article  ADS  CAS  Google Scholar

  * Taglieber, M. _et al._ Simultaneous magneto-optical trapping of three atomic species. _Phys. Rev. A_ 73, 011402. https://doi.org/10.1103/PhysRevA.73.011402 (2006). Article  ADS  CAS 

Google Scholar  * Taglieber, M., Voigt, A.-C., Aoki, T., Hänsch, T. W. & Dieckmann, K. Quantum degenerate two-species Fermi-Fermi mixture coexisting with a Bose-Einstein condensate.

_Phys. Rev. Lett._ 100, 010401. https://doi.org/10.1103/PhysRevLett.100.010401 (2008). Article  ADS  CAS  Google Scholar  * Serwane, F. _et al._ Deterministic preparation of a tunable

few-fermion system. _Science_ 332, 336–338 (2011). Article  ADS  CAS  Google Scholar  * Zürn, G. _et al._ Fermionization of two distinguishable fermions. _Phys. Rev. Lett._ 108, 075303.

https://doi.org/10.1103/PhysRevLett.108.075303 (2012). Article  ADS  CAS  Google Scholar  * Chin, C., Grimm, R., Julienne, P. & Tiesinga, E. Feshbach resonances in ultracold gases. _Rev.

Mod. Phys._ 82, 1225–1286. https://doi.org/10.1103/RevModPhys.82.1225 (2010). Article  ADS  CAS  Google Scholar  * Blume, D. Few-body physics with ultracold atomic and molecular systems in

traps. _Rep. Prog. Phys._ 75, 046401. https://doi.org/10.1088/0034-4885/75/4/046401 (2012). Article  ADS  CAS  Google Scholar  * Zinner, N. T. Exploring the few- to many-body crossover using

cold atoms in one dimension. In _EPJ Web of Conferences_ Vol. 113, 01002 (2016). https://doi.org/10.1051/epjconf/201611301002. * Sowiński, T. & García-March, M. Á. One-dimensional

mixtures of several ultracold atoms: A review. _Rep. Prog. Phys._ 82, 104401. https://doi.org/10.1088/1361-6633/ab3a80 (2019). Article  ADS  MathSciNet  CAS  Google Scholar  * Mistakidis, S.

I. _et al._ Cold atoms in low dimensions—A laboratory for quantum dynamics. arXivy preprint arXiv:2202.11071 (2022). * Giri, M. K., Mondal, S., Das, B. P. & Mishra, T. Signatures of

nontrivial pairing in the quantum walk of two-component bosons. _Phys. Rev. Lett._ 129, 050601. https://doi.org/10.1103/PhysRevLett.129.050601 (2022). Article  ADS  CAS  Google Scholar  *

Campbell, S., García-March, M. A., Fogarty, T. & Busch, T. Quenching small quantum gases: Genesis of the orthogonality catastrophe. _Phys. Rev. A_ 90, 013617.

https://doi.org/10.1103/PhysRevA.90.013617 (2014). Article  ADS  CAS  Google Scholar  * García-March, M. Á., Fogarty, T., Campbell, S., Busch, T. & Paternostro, M. Non-equilibrium

thermodynamics of harmonically trapped bosons. _New J. Phys._ 18, 103035. https://doi.org/10.1088/1367-2630/18/10/103035 (2016). Article  CAS  Google Scholar  * Quan, H. T., Song, Z., Liu,

X. F., Zanardi, P. & Sun, C. P. Decay of Loschmidt echo enhanced by quantum criticality. _Phys. Rev. Lett._ 96, 140604. https://doi.org/10.1103/PhysRevLett.96.140604 (2006). Article  ADS

  CAS  Google Scholar  * Zanardi, P. & Paunković, N. Ground state overlap and quantum phase transitions. _Phys. Rev. E_ 74, 031123. https://doi.org/10.1103/PhysRevE.74.031123 (2006).

Article  ADS  MathSciNet  CAS  Google Scholar  * Benini, L., Naldesi, P., Römer, R. A. & Roscilde, T. Loschmidt echo singularities as dynamical signatures of strongly localized phases.

_New J. Phys._ 23, 023030. https://doi.org/10.1088/1367-2630/abdf9d (2021). Article  ADS  MathSciNet  CAS  Google Scholar  * Lacki, M. & Heyl, M. Dynamical quantum phase transitions in

collapse and revival oscillations of a quenched superfluid. _Phys. Rev. B_ 99, 121107. https://doi.org/10.1103/PhysRevB.99.121107 (2019). Article  ADS  CAS  Google Scholar  * Heyl, M.,

Polkovnikov, A. & Kehrein, S. Dynamical quantum phase transitions in the transverse-field Ising model. _Phys. Rev. Lett._ 110, 135704. https://doi.org/10.1103/PhysRevLett.110.135704

(2013). Article  ADS  CAS  Google Scholar  * Mera, B., Vlachou, C., Paunković, N., Vieira, V. R. & Viyuela, O. Dynamical phase transitions at finite temperature from fidelity and

interferometric Loschmidt echo induced metrics. _Phys. Rev. B_ 97, 094110. https://doi.org/10.1103/PhysRevB.97.094110 (2018). Article  ADS  CAS  Google Scholar  * Knap, M. _et al._

Time-dependent impurity in ultracold fermions: Orthogonality catastrophe and beyond. _Phys. Rev. X_ 2, 041020. https://doi.org/10.1103/PhysRevX.2.041020 (2012). Article  CAS  Google Scholar

  * Halimeh, J. C., Kolley, F. & McCulloch, I. P. Chebyshev matrix product state approach for time evolution. _Phys. Rev. B_ 92, 115130. https://doi.org/10.1103/PhysRevB.92.115130

(2015). Article  ADS  CAS  Google Scholar  * Leforestier, C. _et al._ A comparison of different propagation schemes for the time dependent Schrödinger equation. _J. Comput. Phys._ 94, 59–80

(1991). Article  ADS  MathSciNet  MATH  Google Scholar  * Mistakidis, S. I., Cao, L. & Schmelcher, P. Negative-quench-induced excitation dynamics for ultracold bosons in one-dimensional

lattices. _Phys. Rev. A_ 91, 033611. https://doi.org/10.1103/PhysRevA.91.033611 (2015). Article  ADS  CAS  Google Scholar  * Mistakidis, S. I. & Schmelcher, P. Mode coupling of

interaction quenched ultracold few-boson ensembles in periodically driven lattices. _Phys. Rev. A_ 95, 013625. https://doi.org/10.1103/PhysRevA.95.013625 (2017). Article  ADS  Google Scholar

  * Mistakidis, S. I., Katsimiga, G. C., Kevrekidis, P. G. & Schmelcher, P. Correlation effects in the quench-induced phase separation dynamics of a two species ultracold quantum gas.

_New J. Phys._ 20, 043052. https://doi.org/10.1088/1367-2630/aabc6a (2018). Article  ADS  CAS  Google Scholar  * Erdmann, J., Mistakidis, S. I. & Schmelcher, P. Phase-separation dynamics

induced by an interaction quench of a correlated Fermi-Fermi mixture in a double well. _Phys. Rev. A_ 99, 013605. https://doi.org/10.1103/PhysRevA.99.013605 (2019). Article  ADS  CAS 

Google Scholar  * Mukherjee, K., Mistakidis, S. I., Majumder, S. & Schmelcher, P. Induced interactions and quench dynamics of bosonic impurities immersed in a Fermi sea. _Phys. Rev. A_

102, 053317. https://doi.org/10.1103/PhysRevA.102.053317 (2020). Article  ADS  CAS  Google Scholar  * Olshanii, M. Atomic scattering in the presence of an external confinement and a gas of

impenetrable bosons. _Phys. Rev. Lett._ 81, 938–941. https://doi.org/10.1103/PhysRevLett.81.938 (1998). Article  ADS  CAS  Google Scholar  * Rojo-Francàs, A., Polls, A. & Juliá-Díaz, B.

Static and dynamic properties of a few spin 1/2 interacting fermions trapped in a harmonic potential. _Mathematics_ 8, 1196 (2020). Article  Google Scholar  * Haugset, T. & Haugerud, H.

Exact diagonalization of the Hamiltonian for trapped interacting bosons in lower dimensions. _Phys. Rev. A_ 57, 3809–3817. https://doi.org/10.1103/PhysRevA.57.3809 (1998). Article  ADS  CAS

  Google Scholar  * Raventós, D., Graß, T., Lewenstein, M. & Juliá-Díaz, B. Cold bosons in optical lattices: A tutorial for exact diagonalization. _J. Phys. B At. Mol. Opt. Phys._ 50,

113001. https://doi.org/10.1088/1361-6455/aa68b1 (2017). Article  ADS  CAS  Google Scholar  * Chrostowski, A. & Sowiński, T. Efficient construction of many-body Fock states having the

lowest energies. _Acta Phys. Pol. A_ 136, 566–570. https://doi.org/10.12693/APhysPolA.136.566 (2019). Article  ADS  CAS  Google Scholar  * Kehrberger, L. M. A., Bolsinger, V. J. &

Schmelcher, P. Quantum dynamics of two trapped bosons following infinite interaction quenches. _Phys. Rev. A_ 97, 013606. https://doi.org/10.1103/PhysRevA.97.013606 (2018). Article  ADS  CAS

  Google Scholar  * García, J. H., Covaci, L. & Rappoport, T. G. Real-space calculation of the conductivity tensor for disordered topological matter. _Phys. Rev. Lett._ 114, 116602.

https://doi.org/10.1103/PhysRevLett.114.116602 (2015). Article  ADS  CAS  Google Scholar  * Halimeh, J. C., Kolley, F. & McCulloch, I. P. Chebyshev matrix product state approach for time

evolution. _Phys. Rev. B_ 92, 115130. https://doi.org/10.1103/PhysRevB.92.115130 (2015). Article  ADS  CAS  Google Scholar  * Dobrovitski, V. V. & De Raedt, H. A. Efficient scheme for

numerical simulations of the spin-bath decoherence. _Phys. Rev. E_ 67, 056702. https://doi.org/10.1103/PhysRevE.67.056702 (2003). Article  ADS  CAS  Google Scholar  * Leforestier, C. _et

al._ A comparison of different propagation schemes for the time dependent Schrödinger equation. _J. Comput. Phys._ 94, 59–80 (1991). Article  ADS  MathSciNet  MATH  Google Scholar  *

Mistakidis, S. I., Koutentakis, G. M., Katsimiga, G. C., Busch, T. & Schmelcher, P. Many-body quantum dynamics and induced correlations of Bose polarons. _New J. Phys._ 22, 043007.

https://doi.org/10.1088/1367-2630/ab7599 (2020). Article  ADS  MathSciNet  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS D.K.N. gratefully acknowledges the funding support by the

Institute for Basic Science in Korea (Grant No. IBS-R024-D1). D.K.N. also acknowledges the use of the high-performance computing facility (FERMI cluster) at IBS-PCS. AUTHOR INFORMATION

AUTHORS AND AFFILIATIONS * Center for Theoretical Physics of Complex Systems, Institute for Basic Science (IBS), Daejeon, 34126, Korea Dillip K. Nandy * Institute of Physics, Polish Academy

of Sciences, Aleja Lotników 32/46, 02668, Warsaw, Poland Tomasz Sowiński Authors * Dillip K. Nandy View author publications You can also search for this author inPubMed Google Scholar *

Tomasz Sowiński View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS D.K.N., and T.S. equally contributed in all stages of the project. All

authors reviewed the manuscript. CORRESPONDING AUTHOR Correspondence to Dillip K. Nandy. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL

INFORMATION PUBLISHER'S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. The original online version of this

Article was revised: The original version of this Article contained an error in Reference 10. The correct reference is listed here: Das, S. Particle scattering by harmonically trapped

quantum gases in an artificial magnetic field. _Physica B: Condensed Matter_ 635, 413833. https://doi.org/10.1016/j.physb.2022.413833 (2022). RIGHTS AND PERMISSIONS OPEN ACCESS This article

is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give

appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in

this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's

Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.

To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Nandy, D.K., Sowiński, T. Sudden quench of

harmonically trapped mass-imbalanced fermions. _Sci Rep_ 12, 19710 (2022). https://doi.org/10.1038/s41598-022-24228-z Download citation * Received: 17 October 2022 * Accepted: 11 November

2022 * Published: 16 November 2022 * DOI: https://doi.org/10.1038/s41598-022-24228-z SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get

shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative