Reader TTS

ABSTRACT Complex structure formation inside or through turbid media is a challenging task due to refractive index inhomogeneity, random light scattering, and speckle noise formation. In this

article, we have coupled the data regression model in the R-squared metric and used its advantages as a fitness function in the genetic algorithm to advance the resolution and structural

uniformity. As a compatible system with the binary genetic algorithm, we have presented a cost-effective iterative wavefront shaping system-design with binary phase modulation using an

affordable ferroelectric liquid crystal (FLC) based binary-phase spatial light modulator (SLM). R-squared metric in the genetic algorithm is analyzed to optimize the binary phase mask, and

the prototype system based on iterative binary phase modulation has been validated with a 120-grit ground glass diffuser and fresh chicken tissues of thickness 307 \({\upmu }\text {m}\) and

812 \({\upmu }\text {m}\). The detailed results show that the proposed cost-effective wavefront shaping system with data regression model assisted R-squared fitness function can construct

high-resolution multiple complex hetero-structures simultaneously in 3D volume using an optimized single phase-mask. SIMILAR CONTENT BEING VIEWED BY OTHERS ANTI-SCATTERING LIGHT FOCUSING BY

FAST WAVEFRONT SHAPING BASED ON MULTI-PIXEL ENCODED DIGITAL-MICROMIRROR DEVICE Article Open access 20 July 2021 IMAGE-GUIDED COMPUTATIONAL HOLOGRAPHIC WAVEFRONT SHAPING Article 18 October

2024 3D SCATTERING MICROPHANTOM SAMPLE TO ASSESS QUANTITATIVE ACCURACY IN TOMOGRAPHIC PHASE MICROSCOPY TECHNIQUES Article Open access 15 November 2022 INTRODUCTION Scattering of light in

living or non-living tissue and other disordered media is one of the primary challenges in biomedical imaging, deep tissue imaging, biomedical engineering, and is an active research area in

the adaptive optics and bio-engineering community1,2,3,4,5,6,7,8,9. Focusing light through scattering media such as tissue has many applications in structural light illumination

microscopy10, fluorescence imaging7,11, live cell imaging, neuron excitation/imaging12,13, optical trapping14, and holographyic display. Scientists worldwide are currently engaged in

addressing the challenges arising from scattering in various types of optical and radiation-based biomedical imaging1,4,5,6,7,8,9,10,11,12,13. Inhomogeneity of refractive index in the

medium, repeated random scattering, and speckle noise due to local interference of light cause an unavoidable distortion of the wavefront1,4,15. Modulation of the incident wavefront using

spatial light modulator (SLM)1,4,5,6 enables the focusing of light inside or through scattering media, and it has been initially demonstrated experimentally by Vellekoop and Mosk in 200716.

Wavefront shaping is mostly performed using an iterative, transmission matrix (TM), and digital optical phase conjugation (DOPC) approach1,4,16,17,18,19,20,21,22,23,24. Recently, it has been

observed that evolution-inspired iterative optimization algorithms like genetic algorithm (GA) are well suited for the problem25,26,27,28. Relevant studies have shown that genetic

algorithms perform better in terms of enhancement compared to previously introduced iterative and TM approaches, even in highly noisy environments25,26,27. Feedback-based wavefront shaping

techniques have been explored using various iterative computational algorithms and adaptive optics16,25,26,27,29,30,31,32,33,34. It is also reported in the literature that derivative-free

GA35,36 based feed back technique is quite effective in neutralizing phase aberration and coping with dynamic noisy environments. A fitness function is used for optimization in iterative

feedback-based algorithms to get the desired output. Recently, fitness functions such as target pixels intensity16,32, peak-to-background ratio (PBR)31,37, Pearson’s correlation

coefficient38,39, and standard deviation28, etc have been reported. The selection of fitness functions to optimize solutions within specific segments involves a trade-off between the

advantages and disadvantages of each approach. For example, intensity16,32 and PBR31,37 based fitness functions are common and have been used widely for focusing light through scattering

media. Target intensity based fitness function enhances the intensity at the target spot but shows a noisy background, whereas the PBR based fitness function shows better target intensity

and suppressed background intensity31. However, both fitness functions are unable to form desired patterns with sufficiently high resolution and structural uniformity15,39. A couple of

fitness functions have been reported to form different types of light structure in the literature28,39. The formation of structured light through and inside scattering media has several

potential applications in the real world problems, such as, in the field of holographic displays40, structured light illumination based microscopy10, and photolithography. Recently,

sequential or temporal 3D holography through scattering media using multiple phase masks has been reported40,41,42,43. In 2016, Zhuang et al.41 demonstrated color imaging through turbid

media by considering the memory effect and the point spread function of the optical system. In 2017, Yu et al.40 demonstrated the plane-wise projection of dotted patterns in 3D space

sequentially at different time frames, which have been acquired by translating a three-axis motorized stage. In 2018, Zhao et al.42 used the computer-generated holography based

point-spread-function (PSF) technique for wavefront shaping where the axial scanning of the focus was realized digitally using a digital micromirror device. In 2019, Tran et al.43 proposed a

technique to implement feedback-based wavefront shaping with optical memory effect, where they have shown a lateral distance of 200 \({\upmu }\text {m}\) between focus spots in 3D. However,

it is well known that the optical memory effect is limited in its angular range and tilt direction43,44. In 2022, Lee et al.45 proposed a gradient descent algorithm based 3D color

holography in the open air by projecting multiple independent holograms using temporal multiplexing technique. In our work, we have demonstrated _simultaneous_ multiple complex

hetero-structures formation through tissue like scattering media in 3D volume using a single binary phase mask optimized with R-squared fitness function. On the experimental side,

demonstrations have been conducted using either a nematic liquid crystal SLM (NLC-SLM)46,47,48,49 or a digital micro-mirror device (DMD)27,51. Despite the introduction of different types of

algorithms, advanced hardware such as fast cameras, high-resolution NLC-SLMs, or digital micro-mirror devices (DMDs) are still out of reach for most of the research groups due to their high

cost. The DMDs have a faster refresh rate (\(\sim 23\, \textrm{kHz}\))46,47 and low latency. On the other hand, NLC-SLMs have high latency and low frame rate (\(\sim 60\,

\textrm{Hz}\))27,51. However, DMDs can only achieve binary amplitude modulation, which reduces the enhancement factor compared to the phase modulation achieved by either binary FLC-SLMs (two

discrete phase levels) or NLC-SLMs (256 discrete phase levels)51. The theoretical enhancement factor (\(\eta\)) of binary phase modulation with FLC-SLM is double compared to DMD15,51.

Furthermore, the alignment of DMD is difficult due to its sensitivity to oblique reflection, and it is limited to low-intensity pulsed lasers only48,49. For an NLC-SLM, phase calibration is

mandatory, whereas an FLC-SLM does not require any phase calibration. FLC-SLM is faster than NLC-SLM since it operates in binary mode. FLC-SLM offers a cost-effective alternative with rapid

binary phase modulation (up to 4.5 \(\textrm{kHz}\)), and exhibits increased enhancement compared to DMDs. The use of FLC-SLM for focusing light in scattering media has been shown using the

DOPC-based wavefront shaping technique51. However, DOPC techniques have some unavoidable drawbacks, such as camera pixels and SLM pixels must be in a near-perfect match which makes

alignments far more challenging23,52. Furthermore, the most challenging task is that the SLM and camera have to be at the exact mirror conjugate plane23,52. In this article, a cost-effective

iterative wavefront shaping system has been designed using binary phase capabilities of FLC-SLM and dual cameras to construct multiple non-similar complex structures at different depths

simultaneously in 3D volume using a single binary phase-mask. To achieve multiple complex structures simultaneously, we have utilized the advantages of the R-squared metric as a fitness

function in the genetic algorithm. The FLC-SLM has a pixel switching response time of 40 \({\upmu }\text {s}\) with a refresh rate of up to 4.5 \(\textrm{kHz}\) at present53. The high

refresh rate, high-speed pixel switching time, and binary phase features of FLC-SLM can be utilized to advance the resolution in lesser time. We have validated the prototype system using a

120 grit ground glass (GG) diffuser along with 307 \({\upmu }\text {m}\) and 812 \({\upmu }\text {m}\) thick fresh ex-vivo chicken tissues. Multiple complex light structures and gradient

contrast light formation with R-squared fitness function will find new applications in 3D holographic display40,43, photo-thermal imaging and therapy, fluorescence imaging7,11, light sheet

microscopy54,55, photoacoustic microscopy56, and structure illumination microscopy10. RESULTS AND DISCUSSION The fitness function in iterative optimization algorithms is essential to reach

the optimum solution. It has been observed that the data regression assisted R-squared fitness function, and the most commonly used peak-to-background ratio (PBR) fitness function perform

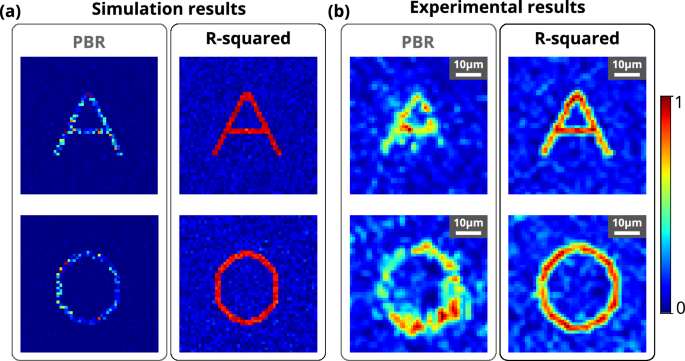
differently based on the complexity of the structure at the region of interest (ROI). Figure 1 shows that the PBR-based fitness function has not been able to resolve the structure and did

not achieve uniform intensity at the target pixels for complex structures such as alphabet letters A and O. A uniform intensity distribution over all pixels at the target location is

essential to resolve complex structures. In the experiment, the PBR-based fitness function is not able to construct a complex structure such as the alphabet letter A and O (see Fig. 2).

However, the R-squared metric-based fitness function outperforms PBR in terms of constructing the structures by enhancing the resolution and structural uniformity. The insets of Figs. 1 and 

2 show the images of the constructed structures A, O and histograms of the intensity distribution in the target area for both the R-squared metric and the PBR fitness functions,

respectively. The R-squared metric is a measure of variance between two data sets57,58, and it has been used frequently in machine learning59. R-SQUARED METRIC AND REGRESSION MODEL ANALYSIS

Regression analysis is a statistical method that estimates the relationship between dependent (reference image (_I_)) and independent (obtained image (_S_)) variables58, where \(S =\left\{

S_j \mid j=1,2, \ldots n\right\}\) represents the intensity of pixels of the obtained image and \(I =\left\{ I_j \mid j=1,2, \ldots n\right\}\) represents the intensity of pixels of the

reference image (_I_). A non-linear regression model \(f =\left\{ f_j \mid j=1,2, \ldots n\right\}\) is formulated with the pixels of the obtained camera image and the pixels of the

reference image as; $$\begin{aligned} f_j = b_0 + {b_1}{S_j} + {b_2}{S_j}^2 + {b_3}{S_j}^3+\cdots +\cdots \end{aligned}$$ (1) where \(b_0\), \(b_1\) represent the linear parameters and

\(b_2\), \(b_3\) represent the higher order parameters in the regression model. However, for simplicity, we have restricted it within the linear regression. The linear regression model is

expressed as follows; $$\begin{aligned} f=\left[ \begin{array}{c} {f}_1 \\ {f}_2 \\ \vdots \\ {f}_n \end{array}\right] =\left[ \begin{array}{c} b_0+b_1 S_1 \\ b_0+b_1 S_2 \\ \vdots \\

b_0+b_1 S_n \end{array}\right] =\left[ \begin{array}{cc} 1 &{} S_1 \\ 1 &{} S_2 \\ \vdots &{} \vdots \\ 1 &{} S_n \end{array}\right] \left[ \begin{array}{l} b_0 \\ b_1

\end{array}\right] \end{aligned}$$ (2) Figure 3 shows the linear regression for the R-squared fitness function. Figure 3a represents the initial linear fit of the reference image (_I_) and

obtained image (_S_) before starting optimization. Whereas, Fig. 3b shows the optimized linear fit of the reference image (_I_) and obtained image (_S_) after 700 iterations. Similarly,

higher-order regression can also be analyzed further with a suitable non-linear regression model. Further, the linear regression model described above is used to formulate the R-squared

fitness function as follows; $$\begin{aligned} R^2 = 1 - \frac{\sum _{j=1}^\text {N} (I_j - \textit{f}_j)^2}{\sum _{j=1}^\text {N} ({I_j - {\overline{I}}})^2},\qquad \textit{where}

\,\,\,{\overline{I}} = \frac{1}{\text {N}} \sum _{j=1}^\text {N} I_j \end{aligned}$$ (3) This R-squared coefficient value lies between 0 and 1. It quantifies the relationship between the

movement of a dependent variable and an independent variable. Its coefficient value 1 refers to a perfect match between the two sets of data, and the value close to 0 represents no linear

relationship between the two data sets57. Detailed analyses of structural uniformity, resolution enhancement, and background noise suppression in the presence of varying noise percentages

for the PBR and R-squared fitness function are shown in Figs. S3–S4 (Supplementary material). CROSS-CORRELATION METRIC TO QUANTIFY STRUCTURAL LIGHT A mathematical function or metric is

essential to quantify the uniformity of the constructed light structure and its similarity test with respect to a reference image. For this, the cross-power spectrum has been implemented to

estimate the cross-correlation metric (CCM) using the obtained image (_S_) and the reference image (_I_). Cross-power spectrum analysis is a technique commonly used in signal processing to

quantify the similarity between two signals or images60. It compares the power spectra of two signals or images to identify common frequency components to measure the similarity. The

cross-power spectrum is calculated by multiplying the complex conjugate of the Fourier transform _S_(_u_, _v_) of the obtained image _S_(_x_, _y_) by the Fourier transform _I_(_u_, _v_) of

the reference image _I_(_x_, _y_). This gives a complex-valued cross-power spectrum, which is further normalized by dividing it by the magnitude of the cross-power spectrum. The normalized

cross-power spectrum \(C_P(u,v)\) of the obtained image _S_(_x_, _y_) and the reference image _I_(_x_, _y_) is calculated as follows; $$\begin{aligned} C_P(u,v) = \dfrac{ I^{*}(u,v) \cdot

S(u,v) }{\left| I^{*}(u,v) \cdot S(u,v) \right| } \end{aligned}$$ (4) Similarly, for normalization, the power spectrum \(R_P(u,v)\) of the reference image (_I_) is calculated by multiplying

its Fourier transform with its complex conjugate and, then normalizing it as; $$\begin{aligned} R_P(u,v) = \dfrac{ I^{*}(u,v) \cdot I(u,v) }{\left| I^{*}(u,v) \cdot I(u,v) \right| }

\end{aligned}$$ (5) The \(C_P(u,v)\) and \(R_P(u,v)\) are in the frequency domain. To visualize and interpret the results in the spatial domain, the inverse Fourier transform converts the

spectra back into the spatial domain \(C_P(x,y)\) and \(R_P(x,y)\). Finally, a cross-correlation metric (CCM) is calculated by dividing the maximum value of \(\left| C_p(x,y) \right| )\)  

with the maximum value of \(\left| R_p(x,y)\right|\). The final cross-correlation metric (CCM) is written as follows; $$\begin{aligned} \text {Cross-correlation metric} = \dfrac{max(\left|

C_p(x,y) \right| )}{max(\left| R_p(x,y)\right| )} \end{aligned}$$ (6) The cross-correlation metric measures the similarity of two images. If the metric variable is close to 1, the images are

similar, while if it is close to 0, they are significantly different61. Figure 4 shows the analysis of the metric value using simulation and experimental data over 700 generations for both

the PBR and R-squared fitness functions. CHARACTERIZATION OF EXPERIMENTAL SETUP AND FORMATION OF 2D/3D COMPLEX STRUCTURES THROUGH BIOLOGICAL TISSUE MEDIA The detailed schematic of the

experimental system-design with various hardware building blocks, tissue samples for the experiment, and the constructed 3D volume image is shown in Fig. 5. The system design consists of a

master controller, i.e., the FLC-SLM hardware driver. This hardware driver is connected further with the responders, i.e., the FLC-SLM’s microdisplay unit and the arbitrary function

generator, which triggers both the cameras. The light from a He–Ne laser of wavelength 633 nm passes through a spatial filter and falls on the SLM. Subsequently, the wavefront modulated by

the FLC-SLM propagates through a series of optical components and falls on the scattering media. To facilitate the formation of multiple complex hetero-structures _simultaneously_ at

different depths in the 3D volume, a beam splitter is used to split the speckle field into two parts. These two parts are imaged by cameras placed at two different depths. Camera-1 is placed

at distance \(\mathrm {D_1}\), which has the option of moving back and forth. Camera-2 is placed at distance \(\mathrm {D_2}\) to visualize the 3D volume. Furthermore, a set of sequential

hardware operation instructions are sent from the personal computer to the FLC-SLM display head and the cameras for acquiring the output speckle field generated by the tissue sample. The

working principle of the FLC-SLM is shown briefly in Fig. 5a and a more detailed overview is shown in Fig. S14 (Supplementary material). The experiment has been performed with the developed

system, where both the PBR and the R-squared fitness function have been tested to focus the complex 2D as well as 3D structures. A commercial 120-grit GG diffuser has been used as the

scattering medium. Chicken tissue samples of thickness 307 \({\upmu }\text {m}\) and 812 \({\upmu }\text {m}\) have been used for demonstration. Formation of the complex patterns through the

GG diffuser is shown in Fig. 1. It has been observed that standard PBR is not able to focus complex structures such as the alphabet letters A and O clearly, while the R-squared fitness

function is able to form well-resolved A and O through a highly scattering 120-grit GG diffuser. The word ‘IISER’ has also been constructed through the 120-grit GG diffuser to demonstrate a

more complex 2D structure formation. The result is shown in Fig. S1 (Supplementary material), where it has been observed that the R-squared fitness function efficiently forms the structure

IISER, while PBR is not able to form it. Furthermore, a plus sign structure consisting four gradient grayscale based target pixels along each arm and one grayscale based background pixels

has also been constructed through 120-grit GG diffuser. The results for plus structure are shown in Fig. 6, where it has been observed that the R-squared fitness function is able to

construct gradient contrast along each arm of plus sign structure in both simulation and experiment, while PBR is not able to form it. It has also been observed that the lower value

contrast, which is near the background intensity, spreads all around the structure while PBR fitness function is considered. The stability of the experimental setup has been demonstrated

with chicken tissue samples of thickness 307 \({\upmu }\text {m}\) and 812 \({\upmu }\text {m}\). Figure 7 shows the formation of complex structures through chicken tissues for the standard

PBR and the R-squared fitness function. Similar to the GG diffuser results, the R-squared fitness function outperforms the standard PBR in terms of advancing the resolution, structural

uniformity, and background suppression for complex structure formation through chicken tissue. As the thickness of the tissue sample has been increased to 815 \({\upmu }\text {m}\), still

R-squared fitness function has shown well-resolved structure formation compared to the standard PBR. SIMULTANEOUS FORMATION OF MULTIPLE COMPLEX HETERO-STRUCTURES IN 3D SPACE THROUGH TISSUE

In this work, an experimental system with dual cameras has been proposed (Figs. 5, 10), which simultaneously facilitates the construction of multiple complex structures in a 3D space (Fig. 

8). The proposed setup is able to construct structures in a much larger 3D volume compared to the volume covered with angular range and tilt direction of the optical memory effect. With the

R-squared fitness function and the experimental setup, multiple complex structures have been constructed _simultaneously_ at different planes of 3D volume by displaying an optimized single

phase-mask on the FLC-SLM. A fresh chicken tissue of thickness 565 \({\upmu }\text {m}\) has been used as a scattering medium. A phase mask has been optimized using the R-squared fitness

function in the genetic algorithm35 and displayed on the FLC-SLM to form complex structures in multiple planes in 3D space. Figure 8 shows the 3D volume slice images of the formation of A

and O structures through chicken tissue using a single optimized phase mask. The axial and lateral distances between the two complex objects have been kept at 1.62 \(\text {mm}\) and 266 

\({\upmu }\text {m}\), respectively. The resolution of the system has been estimated with the objective lens (10\(\times\), 0.25 NA) at wavelength 633 nm and found to be \(88.15\,\pm

2\,{\upmu }\text {m}\). The detailed system resolution and more complex volume imaging with multiple images in 3D volume are shown in the Supporting information (Section S4.3, Fig. S16).

CONCLUSION AND PERSPECTIVES In the field of wavefront shaping, it is crucial to pursue objectives such as increasing the efficiency of light transmission through turbid media, enhancing

resolution, developing structural light uniformly, forming gradient contrast in light structures, and achieving a precise focus that allows 2D or 3D light structure formation through

scattering media. Our experimental setup demonstrates notable advancements in resolution and structural uniformity, which facilitates the formation of multiple light structures within a 3D

volume through the scattering media (Fig. 8). A data regression model based R-squared fitness function has been introduced into the algorithm and implemented in the FLC-SLM based iterative

binary phase modulation system (Fig. 3). The prototype system with R-Squared fitness function has shown remarkable performance in improving structural uniformity and resolution (Figs. 1, 2, 

6, 7,  8). The developed cost-effective and calibration-free (wavelength independent phase calibration) iterative wavefront shaping system along with R-squared fitness function has been

validated with a 120-grit GG diffuser along with fresh ex-vivo chicken tissue samples of thickness 307 \({\upmu }\text {m}\) and 812 \({\upmu }\text {m}\) (Figs. 7, 8). A cross-correlation

based metric (CCM) has also been analyzed to quantify the structural similarity of the constructed light structures. Simulation results show that R-squared fitness function has achieved up

to 81.4% CCM value where PBR has achieved below 30.1% CCM value for light structure A (Fig. 4). Similarly, experimental results show that R-squared has been able to achieve up to 33% CCM

value whereas PBR has achieved only 11% for light structure A (Fig. 4). The standard deviation analysis shows that R-squared fitness function has achieved substantial improvement in the

uniformity of intensity at target and background pixels compared to the PBR fitness function (Figs. S10, S11, Supplementary material). The fitness value for PBR has shown progression with

the generation, but it failed to construct the structure, whereas R-squared fitness function has shown well-resolved structure (Fig. 9). The proposed method has demonstrated robust noise

tolerance while varying the noise percentage from 10 to 100%, and the results are shown in Figs. S2, S3 (Supplementary material). The impact of  input modes (_N_) variation has also been  

analyzed for the PBR and R-squared fitness functions in both the simulation and experiment. Detailed results for the input modes analysis are shown in Figs. S4–S9. The designed system with

the dual cameras and R-squared fitness function has constructed high-resolution, non-similar multiple complex structures (A/O shapes) simultaneously at different depths in 3D using an

optimized single phase-mask. This work may find potential applications in 3D confocal microscopy, 3D photoacoustic microscopy, photolithography, structured light illumination microscopy, 3D

holography, and photothermal therapy. However, the efficiency of the SLM decreases with increasing the number of complex structures as a result of the limited availability of optimized input

modes. The other advanced functionalities of the FLC-SLM, including RGB data transfer using three color channels and its wavelength-independent phase calibration, provide an advantage in

designing new experiments. The fast pixel-switching time (\(40 \, {\upmu }\text {s}\)) and a high refresh rate of \(4.5 \, \textrm{kHz}\)53 make the FLC-SLM suitable for applications such as

tissue imaging, live cell imaging, and photoacoustic microscopy. Despite advancements in algorithms and SLM refresh rate, the operating speed of the entire system is bottlenecked by the

slow data transfer rate between the camera and the PC. However, the delay in data transfer from the camera to the PC can be reduced drastically using a multichannel data transfer protocol

like _CoaXPress_. A faster acquisition speed will further reduce the number of iterations required to reach convergence, as it will reduce the noises generated due to beam shifts,

temperature fluctuations, and the camera sensor’s response. These advantages and cost-effectiveness make the system more suitable for designing various complex wavefront shaping experiments.

METHODS COMPUTATIONAL MODEL The output complex field \(E(d^{'})\) obtained through a scattering media of transmission function \(T(d,d^{'})\), can be written as

\(E(d^{'})\)=\(\sum _{d}T(d,d^{'}) E(d)\). Where the incoming light field is denoted by _E_(_d_). A transmission matrix (_T_) of dimensions \(M \times N\) models wavefront

scattering through disordered media. Here, _T_ is generated by a complex Gaussian random matrix. The equation for the calculation of the output modes _M_ can be written as16,25;

$$\begin{aligned} E_m = \sum _{n}^{N} t_{mn} A_n e^{i{\phi }_n} \end{aligned}$$ (7) where \(A_n\) and \({\phi }_n\) are the amplitude and phase of an input mode (_n_), respectively, and

\(t_{mn}\) is a particular element of the transmission matrix _T_. The amplitude of the complex field is chosen as \(A_n=1/\sqrt{N}\). Therefore, the intensity (\(I_m\)) at a particular

output mode at the camera with added noise can be written as; $$\begin{aligned} I_m = \frac{1}{N}\Bigg |{ \sum _{n}^{N} t_{mn} e^{i{\phi }_n}}\Bigg |^2 +\, \delta \quad \text {where,} \quad

\delta = \frac{\Gamma \%}{100} \times {\mathscr {N}}(\mu _T,\,\sigma _T)\, <I_o> \end{aligned}$$ (8) Here, a noise (\(\delta\)) is added to mimic the experimental environment.

\(\Gamma\) represents the percentage of added noise with respect to the initial average intensity \(<I_o>\). \({\mathscr {N}}(\mu _T,\sigma _T)\) represents a random number generated

from a normal distribution with mean (\(\mu _T\)) and standard deviation (\(\sigma _T\)). The parameters for GA are set according to the optimized values described in the literature15,37. In

feedback algorithms, especially for GA, intensity based fitness function is considered as \({I^{T}_{i}}/ {I^{{\bar{B}}}_{initial}}\), where \(I^{T}_{i}\) is the intensity at target pixels

for _i_th generation and \({I^{{\bar{B}}}_{initial}}\) is the initial average intensity at the background pixels16,32. Whereas, PBR based fitness function is considered as \({I^{T}_{i}}/

{I^{{\bar{B}}}_{i}}\), where \(I^{T}_{i}\) is the intensity at target pixels for _i_th generation and \(I^{{\bar{B}}}_{i}\) is the average intensity at the background pixels for _i_th

generation31,37. However, this article has considered the R-squared metric as a fitness function, which has been discussed thoroughly in the first part of the results and discussion section.

The simulation model has been designed in the Python 3 programming language and NumPy has been used to process the matrices. As per the input mode analysis, an optimized matrix of

dimensions \(250\times 250\) has been considered as the input modes matrix that corresponds to total \(N=62,500\) input modes in the simulation (Figs. S4–S7). On the output side, a matrix of

dimensions \(50\! \times \!50\) has been considered as the output mode matrix that provides \(M=2500\) output modes (\(\vec {E}_{out}\)). The transmission matrix (_T_) of dimensions

\(M\times N\) has been generated using a complex Gaussian random distribution (\(\mu _T = 0\) and \(\sigma _T = 0.1\)) to mimic light scattering. In addition, a 30% noise \(\delta\) has been

added to the output mode intensity to simulate the experimental conditions. In the experiment, an optimized input modes matrix of dimensions \(320\times 256\) has been considered (Figs. S8,

S9). Furthermore, a matrix of dimensions \(50\! \times \!50\) has been considered as the output mode matrix in the experiment. In the beginning of the algorithm, a population (_P_) of

random binary phase masks has been generated using a discrete uniform distribution of values 0 and 255, which correspond to the 0 and \(\pi\) phase, respectively. A population size of 200

has been chosen as it provides a good trade-off between speed and enhancement. Two parents \(\vec {P}_i\) and \(\vec {P}_j\) have been selected with a biased probability toward a higher

fitness value. The descending order of the phase masks has been ranked according to their fitness value, which was later used for the selection of parents. The crossover rate (\(r_c\)) has

been kept at the standard value of 50%. The initial mutation rate has been fixed at 1%, which decays exponentially with a constant decay rate (\(\lambda\))15,37. EXPERIMENTAL SYSTEM DESIGN

WITH FLC-SLM A detailed schematic of experimental setup is shown in Figs. 5 and 10. A 12 mW He–Ne laser (633 nm, Newport), consisting of vertical linearly polarized light with a polarization

ratio of 500:1, is used in the built system. The alignment of the laser beam has been done with the help of two flat mirrors \(\mathrm {M_1}\) and \(\mathrm {M_2}\). Along the path, a

spatial filter system (Thorlabs, KT311/M) is placed consisting of a pinhole (\(\phi =10\, {\upmu }\text {m})\) and objective (20\(\times\), Numerical Aperture (NA) = 0.40) for eliminating

the higher-order noise from the beam. Thereafter, the spatially filtered diverging beam is collimated by a lens \(\mathrm {L_1}\) \((f = 250 \, \text {mm})\) to get a pure flat beam profile

on the surface of FLC-SLM. A polarising beam splitter (PBS) and FLC-SLM (ForthDD, SXGA-R5) are used for the wavefront modulation. The modulated wavefront is passed through a 4_F_ setup and

enters into an objective (10\(\times\), \(\text {NA} = 0.25\)) which transmits the wavefront through the scattering media. The power of the incident beam before entering into the tissue

sample has been measured and found to be 0.74 mW. A second objective (10\(\times\), \(\text {NA} = 0.25\)) is placed behind the scattering media. For the simultaneous construction of

multiple complex structures in 3D volume, the CMOS camera-1 (Thorlabs, DCC3260C) and CMOS camera-2 (Basler acA800-510uc) are placed at distance \(\mathrm {D_1}\) and \(\mathrm {D_2}\),

respectively, to acquire images at different depths in 3D space and make the feedback signals for the algorithm. The CMOS camera-1 has the option to move back and forth to construct multiple

complex structures at more than two different depths. The signal from the PC to the SLM driver module is sent via a video card. Each image is a combination of 24 bit-planes, i.e., 24-bit

information per pixel and 8-bit per channel (RGB). The hardware module of the SLM splits the RGB signal into 24 single-bit black-and-white images. These 24 single-bit images are sent and

displayed on the SLM screen sequentially. In conclusion, a total of \(24\times 60 = 1440\) binary images are displayed on the SLM screen in 1s with these setting parameters. Each bit plane

is displayed on the SLM screen for a duration of 219.02 \({\upmu }\text {s}\). The hardware driver module of the SLM is programmed to generate an output electrical signal which becomes high

or low in synchronization with the display of each bit plane. This signal is passed to the function generator to generate a new signal with \(+3\,\textrm{V}\) to trigger the two CMOS

cameras. The other advanced features of the FLC-SLM, such as three color channels, can be utilized either collectively or individually. The two cameras have been triggered using the function

generator to construct multiple simultaneous complex structures in 3D space. PREPARATION OF CHICKEN TISSUE SAMPLES FOR THE EXPERIMENT The experiment was conducted without the use of live

animals. A part of fresh skinless chicken (weight = 2.62 \(\text {kg}\), age = 10 weeks, measured density = 0.92 \(\mathrm {g/cm}^3\)) was procured from the local market. The chicken thigh

was kept in the freezer for 4 hours at a constant temperature of \(-14 \, ^{\circ }\textrm{C}\) to facilitate the slicing. A sterilized surgical scalpel was used to section the chicken

tissue into multiple slices. The measured thickness of the sliced chicken tissues has been found to be 307 and 812 \({\upmu }\text {m}\) for 2D structure formation, and 565 \({\upmu }\text

{m}\) for 3D multiple structures formation. The sliced chicken muscle was sandwiched between two microscope glass cover-slips. A drop of Glycerol was used to preserve the sample and prevent

it from dehydration. DATA AVAILABILITY The original contributions presented in the study are included in the article and the Supplementary Material; further inquiries can be directed to the

corresponding author. REFERENCES * Vellekoop, I. M., Lagendijk, A. & Mosk, A. P. Exploiting disorder for perfect focusing. _Nat. Photon._ 4, 320–322.

https://doi.org/10.1038/nphoton.2010.3 (2010). Article  CAS  Google Scholar  * Berto, P. _et al._ Tunable and free-form planar optics. _Nat. Photon._ 13, 649–656.

https://doi.org/10.1038/s41566-019-0486-3 (2019). Article  ADS  CAS  Google Scholar  * Wang, D., Sahoo, S. K., Zhu, X., Adamo, G. & Dang, C. Non-invasive super-resolution imaging through

dynamic scattering media. _Nat. Commun._ 12, 3150. https://doi.org/10.1038/s41467-021-23421-4 (2021). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Mosk, A. P., Lagendijk,

A., Lerosey, G. & Fink, M. Controlling waves in space and time for imaging and focusing in complex media. _Nat. Photon._ 6, 283–292. https://doi.org/10.1038/nphoton.2012.88 (2012).

Article  ADS  CAS  Google Scholar  * Ojambati, O. S. Optical energy on demand. _Nat. Phys._ 18, 227–228. https://doi.org/10.1038/s41567-022-01509-y (2022). Article  CAS  Google Scholar  *

Luo, Y., Yan, S., Li, H., Lai, P. & Zheng, Y. Focusing light through scattering media by reinforced hybrid algorithms. _APL Photon._ 5, 016109. https://doi.org/10.1063/1.5131181 (2020).

Article  ADS  CAS  Google Scholar  * Boniface, A., Dong, J. & Gigan, S. Non-invasive focusing and imaging in scattering media with a fluorescence-based transmission matrix. _Nat.

Commun._ 11, 6154. https://doi.org/10.1038/s41467-020-19696-8 (2020). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Conkey, D. B. _et al._ Super-resolution photoacoustic

imaging through a scattering wall. _Nat. Commun._ 6, 7902. https://doi.org/10.1038/ncomms8902 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Arias, A. & Artal, P.

Wavefront-shaping-based correction of optically simulated cataracts. _Optica_ 7, 22–27. https://doi.org/10.1364/OPTICA.7.000022 (2020). Article  ADS  Google Scholar  * Liu, G. _et al._

Combination of structured illumination microscopy with hyperspectral imaging for cell analysis. _Anal. Chem._ 93, 10056–10064. https://doi.org/10.1021/acs.analchem.1c00660 (2021). Article 

CAS  PubMed  Google Scholar  * Vellekoop, I. M. & Aegerter, C. M. Scattered light fluorescence microscopy: Imaging through turbid layers. _Opt. Lett._ 35, 1245–1247.

https://doi.org/10.1364/OL.35.001245 (2010). Article  ADS  PubMed  Google Scholar  * Wilt, B. A. _et al._ Advances in light microscopy for neuroscience. _Annu. Rev. Neurosci._ 32, 435–506.

https://doi.org/10.1146/annurev.neuro.051508.135540 (2009). Article  CAS  PubMed  PubMed Central  Google Scholar  * Dougherty, T. J. _et al._ Photodynamic Therapy. _J. Natl Cancer Inst._ 90,

889–905. https://doi.org/10.1093/jnci/90.12.889 (1998). Article  CAS  PubMed  Google Scholar  * Čižmár, T., Mazilu, M. & Dholakia, K. In situ wavefront correction and its application to

micromanipulation. _Nat. Photon._ 4, 388–394. https://doi.org/10.1038/nphoton.2010.85 (2010). Article  ADS  CAS  Google Scholar  * Vellekoop, I. M. Feedback-based wavefront shaping. _Opt.

Express_ 23, 12189–12206. https://doi.org/10.1364/OE.23.012189 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Vellekoop, I. M. & Mosk, A. P. Focusing coherent light through opaque

strongly scattering media. _Opt. Lett._ 32, 2309–2311. https://doi.org/10.1364/OL.32.002309 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Vellekoop, I. M. & Mosk, A. P. Phase

control algorithms for focusing light through turbid media. _Opt. Commun._ 281, 3071–3080 (2008). Article  ADS  CAS  Google Scholar  * Popoff, S. M. _et al._ Measuring the transmission

matrix in optics: An approach to the study and control of light propagation in disordered media. _Phys. Rev. Lett._ 104, 100601. https://doi.org/10.1103/PhysRevLett.104.100601 (2010).

Article  ADS  CAS  PubMed  Google Scholar  * Popoff, S., Lerosey, G., Fink, M., Boccara, A. C. & Gigan, S. Image transmission through an opaque material. _Nat. Commun._ 1, 81.

https://doi.org/10.1038/ncomms1078 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Cui, M. Parallel wavefront optimization method for focusing light through random scattering media.

_Opt. Lett._ 36, 870–872. https://doi.org/10.1364/OL.36.000870 (2011). Article  ADS  PubMed  Google Scholar  * Stockbridge, C. _et al._ Focusing through dynamic scattering media. _Opt.

Express_ 20, 15086–15092. https://doi.org/10.1364/OE.20.015086 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Yaqoob, Z., Psaltis, D., Feld, M. S. & Yang, C. Optical phase

conjugation for turbidity suppression in biological samples. _Nat. Photon._ 2, 110–115. https://doi.org/10.1038/nphoton.2007.297 (2008). Article  ADS  CAS  Google Scholar  * Cui, M. &

Yang, C. Implementation of a digital optical phase conjugation system and its application to study the robustness of turbidity suppression by phase conjugation. _Opt. Express_ 18, 3444–3455.

https://doi.org/10.1364/OE.18.003444 (2010). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hsieh, C.-L., Pu, Y., Grange, R. & Psaltis, D. Digital phase conjugation of

second harmonic radiation emitted by nanoparticles in turbid media. _Opt. Express_ 18, 12283–12290. https://doi.org/10.1364/OE.18.012283 (2010). Article  ADS  CAS  PubMed  Google Scholar  *

Conkey, D. B., Brown, A. N., Caravaca-Aguirre, A. M. & Piestun, R. Genetic algorithm optimization for focusing through turbid media in noisy environments. _Opt. Express_ 20, 4840–4849.

https://doi.org/10.1364/OE.20.004840 (2012). Article  ADS  PubMed  Google Scholar  * Anderson, B. R., Price, P., Gunawidjaja, R. & Eilers, H. Microgenetic optimization algorithm for

optimal wavefront shaping. _Appl. Opt._ 54, 1485–1491. https://doi.org/10.1364/AO.54.001485 (2015). Article  ADS  PubMed  Google Scholar  * Fang, L., Zhang, X., Zuo, H. & Pang, L.

Focusing light through random scattering media by four-element division algorithm. _Opt. Commun._ 407, 301–310. https://doi.org/10.1016/j.optcom.2017.08.062 (2018). Article  ADS  CAS  Google

Scholar  * Conkey, D. B. & Piestun, R. Color image projection through a strongly scattering wall. _Opt. Express_ 20, 27312–27318. https://doi.org/10.1364/OE.20.027312 (2012). Article 

ADS  PubMed  Google Scholar  * Zhang, B. _et al._ Focusing light through strongly scattering media using genetic algorithm with SBR discriminant. _J. Opt._ 20, 025601.

https://doi.org/10.1088/2040-8986/aa9f91 (2017). Article  ADS  Google Scholar  * Li, R. _et al._ Interleaved segment correction achieves higher improvement factors in using genetic algorithm

to optimize light focusing through scattering media. _J. Opt._ 19, 105602. https://doi.org/10.1088/2040-8986/aa84dc (2017). Article  ADS  PubMed  PubMed Central  Google Scholar  * Zhang, X.

& Kner, P. Binary wavefront optimization using a genetic algorithm. _J. Opt._ 16, 125704. https://doi.org/10.1088/2040-8978/16/12/125704 (2014). Article  ADS  Google Scholar  * Wu, D.,

Luo, J., Li, Z. & Shen, Y. A thorough study on genetic algorithms in feedback-based wavefront shaping. _J. Innov. Opt. Health Sci._ 12, 1942004. https://doi.org/10.1142/S1793545819420045

(2019). Article  Google Scholar  * Kumar, A., Thakur, S. & Biswas, S. Weighted mutation assisted genetic algorithm focuses light tightly through scattering media. In _2022 Workshop on

Recent Advances in Photonics (WRAP)_, 1–2, https://doi.org/10.1109/WRAP54064.2022.9758238 (2022). * Kumar, A., Thakur, S. & Biswas, S. K. Simultaneous control of 3D volume speckle field

and 3D holography through biological tissue. In _Adaptive Optics and Wavefront Control for Biological Systems IX_ Vol. 12388 (eds Bifano, T. G. _et al._) 1238806 (International Society for

Optics and Photonics (SPIE), 2023). https://doi.org/10.1117/12.2650600. Chapter  Google Scholar  * Tehrani, K. F., Xu, J., Zhang, Y., Shen, P. & Kner, P. Adaptive optics stochastic

optical reconstruction microscopy (ao-storm) using a genetic algorithm. _Opt. Express_ 23, 13677–13692. https://doi.org/10.1364/OE.23.013677 (2015). Article  ADS  CAS  PubMed  Google Scholar

  * Yang, P., Xu, B., Jiang, W. & Chen, S. A genetic algorithm used in a 61-element adaptive optical system. _Front. Optoelectron. China_ 1, 263–267.

https://doi.org/10.1007/s12200-008-0068-3 (2008). Article  Google Scholar  * Feng, Q., Zhang, B., Liu, Z., Lin, C. & Ding, Y. Research on intelligent algorithms for amplitude

optimization of wavefront shaping. _Appl. Opt._ 56, 3240–3244. https://doi.org/10.1364/AO.56.003240 (2017). Article  ADS  PubMed  Google Scholar  * He, H., Guan, Y. & Zhou, J. Image

restoration through thin turbid layers by correlation with a known object. _Opt. Express_ 21, 12539–12545. https://doi.org/10.1364/OE.21.012539 (2013). Article  ADS  PubMed  Google Scholar 

* Wan, L., Chen, Z., Huang, H. & Pu, J. Focusing light into desired patterns through turbid media by feedback-based wavefront shaping. _Appl. Phys. B_ 122, 204.

https://doi.org/10.1007/s00340-016-6466-0 (2016). Article  ADS  CAS  Google Scholar  * Yu, H., Lee, K., Park, J. & Park, Y. Ultrahigh-definition dynamic 3d holographic display by active

control of volume speckle fields. _Nat. Photon._ 11, 186–192. https://doi.org/10.1038/nphoton.2016.272 (2017). Article  ADS  CAS  Google Scholar  * Zhuang, H., He, H., Xie, X. & Zhou, J.

High speed color imaging through scattering media with a large field of view. _Sci. Rep._ 6, 32696. https://doi.org/10.1038/srep32696 (2016). Article  ADS  CAS  PubMed  PubMed Central 

Google Scholar  * Zhao, Q. _et al._ 3d focusing through highly scattering media using psf modulation. _Appl. Phys. Lett._ 113, 191104. https://doi.org/10.1063/1.5060710 (2018). Article  ADS

  CAS  Google Scholar  * Tran, V., Sahoo, S. K. & Dang, C. Fast 3d movement of a laser focusing spot behind scattering media by utilizing optical memory effect and optical conjugate

planes. _Sci. Rep._ 9, 19507. https://doi.org/10.1038/s41598-019-56214-3 (2019). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Cao, H. W. Customizing optical memory effect of

scattering media for imaging applications. In _Optical and Quantum Sensing and Precision Metrology II_ Vol. PC12016 (eds Scheuer, J. & Shahriar, S. M.) PC1201624 (International Society

for Optics and Photonics (SPIE), 2022). https://doi.org/10.1117/12.2615435. Chapter  Google Scholar  * Lee, B., Kim, D., Lee, S., Chen, C. & Lee, B. High-contrast, speckle-free, true 3d

holography via binary cgh optimization. _Sci. Rep._ 12, 2811. https://doi.org/10.1038/s41598-022-06405-2 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Conkey, D. B.,

Caravaca-Aguirre, A. M. & Piestun, R. High-speed scattering medium characterization with application to focusing light through turbid media. _Opt. Express_ 20, 1733–1740.

https://doi.org/10.1364/OE.20.001733 (2012). Article  ADS  PubMed  Google Scholar  * Akbulut, D., Huisman, T. J., van Putten, E. G., Vos, W. L. & Mosk, A. P. Focusing light through

random photonic media by binary amplitude modulation. _Opt. Express_ 19, 4017–4029. https://doi.org/10.1364/OE.19.004017 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Wang, D. _et

al._ Focusing through dynamic tissue with millisecond digital optical phase conjugation. _Optica_ 2, 728–735. https://doi.org/10.1364/OPTICA.2.000728 (2015). Article  ADS  CAS  PubMed 

PubMed Central  Google Scholar  * Tay, J. W., Liang, J. & Wang, L. V. Amplitude-masked photoacoustic wavefront shaping and application in flowmetry. _Opt. Lett._ 39, 5499–5502.

https://doi.org/10.1364/OL.39.005499 (2014). Article  ADS  PubMed  PubMed Central  Google Scholar  * Zhao, Y., He, Q., Li, S. & Yang, J. Gradient-assisted focusing light through

scattering media. _Opt. Lett._ 46, 1518–1521. https://doi.org/10.1364/OL.417606 (2021). Article  ADS  PubMed  Google Scholar  * Liu, Y., Ma, C., Shen, Y., Shi, J. & Wang, L. V. Focusing

light inside dynamic scattering media with millisecond digital optical phase conjugation. _Optica_ 4, 280–288. https://doi.org/10.1364/OPTICA.4.000280 (2017). Article  ADS  PubMed  PubMed

Central  Google Scholar  * Vellekoop, I. M., Cui, M. & Yang, C. Digital optical phase conjugation of fluorescence in turbid tissue. _Appl. Phys. Lett._ 101, 081108.

https://doi.org/10.1063/1.4745775 (2012). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Park, C., Lee, K., Baek, Y. & Park, Y. Low-coherence optical diffraction tomography

using a ferroelectric liquid crystal spatial light modulator. _Opt. Express_ 28, 39649–39659. https://doi.org/10.1364/OE.405418 (2020). Article  ADS  CAS  PubMed  Google Scholar  * Yang, Z.

_et al._ Light sheet microscopy with acoustic sample confinement. _Nat. Commun._ 10, 669. https://doi.org/10.1038/s41467-019-08514-5 (2019). Article  ADS  CAS  PubMed  PubMed Central 

Google Scholar  * Shi, Y., Daugird, T. A. & Legant, W. R. A quantitative analysis of various patterns applied in lattice light sheet microscopy. _Nat. Commun._ 13, 4607.

https://doi.org/10.1038/s41467-022-32341-w (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Hazan, Y., Levi, A., Nagli, M. & Rosenthal, A. Silicon-photonics acoustic

detector for optoacoustic micro-tomography. _Nat. Commun._ 13, 1488. https://doi.org/10.1038/s41467-022-29179-7 (2022). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Devore,

J. L. _Probability and Statistics for Engineering and the Sciences_ 8th edn. (Richard Stratton, 2012). Google Scholar  * Steel, R. G. & Torrie, J. H. _Principles and Procedures of

Statistics: With Special Reference to the Biological Sciences_ (McGraw-Hill, 1960). MATH  Google Scholar  * Coelho, L. B. _et al._ Reviewing machine learning of corrosion prediction in a

data-oriented perspective. _NPJ Mater. Degrad._ 6, 8. https://doi.org/10.1038/s41529-022-00218-4 (2022). Article  Google Scholar  * Shynk, J. J. _Probability, Random Variables, and Random

Processes_ (Wiley, 2013). MATH  Google Scholar  * Alan, V. & Oppenheim, R. W. S. _Digital Signal Processing_ (Pearson Education, 2017). MATH  Google Scholar  Download references

ACKNOWLEDGEMENTS The authors are thankful to IISER Mohali startup fund and IMPRINT funding agency for their support. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Bio-NanoPhotonics

Laboratory, Department of Physical Sciences, Indian Institute of Science Education and Research-Mohali, Knowledge City, Sector 81, SAS Nagar, Manauli, PO, 140306, India Amit Kumar, Sarvesh

Thakur & S. K. Biswas Authors * Amit Kumar View author publications You can also search for this author inPubMed Google Scholar * Sarvesh Thakur View author publications You can also

search for this author inPubMed Google Scholar * S. K. Biswas View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.K. designed the

experimental setup. A.K. and S.T. performed the experiment and the simulation analysis. S.K.B. defined the problem and monitored the progress. All authors wrote and reviewed the manuscript.

CORRESPONDING AUTHOR Correspondence to S. K. Biswas. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER'S NOTE Springer

Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. RIGHTS AND PERMISSIONS

OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or

format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or

other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not

included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission

directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Kumar,

A., Thakur, S. & Biswas, S.K. Formation of multiple complex light structures simultaneously in 3D volume using a single binary phase mask. _Sci Rep_ 13, 16951 (2023).

https://doi.org/10.1038/s41598-023-42087-0 Download citation * Received: 01 June 2023 * Accepted: 05 September 2023 * Published: 07 October 2023 * DOI:

https://doi.org/10.1038/s41598-023-42087-0 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative