Reader TTS

ABSTRACT The knowledge of phase relations of constitutive minerals is essential to investigate the structure, dynamics and evolution of the Earth and planetary interiors. This paper reviews

the phase relations of bridgmanite, the most abundant mineral in the Earth’s lower mantle, with an ideal composition of MgSiO3. Bridgmanite has an orthorhombic structure with larger

dodecahedral A and smaller octahedral B cation sites. The A-sites can incorporate Mg2+, Fe2+, Fe3+, and Al3+, while the B-sites accommodate Si4+, Al3+ and Fe3+. The incorporation of hydrogen

and large cations like Ca is likely limited, although these issues are still debated. Al3+ and Fe3+, respectively, can form the charge-coupled components, AlAlO3 and Fe3+Fe3+O3 occupying

both A- and B-sites. When both Al3+ and Fe3+ are present, Al3+ occupies B-sites, and Fe3+ occupies A-sites, forming Fe3+AlO3. In systems with excess MgO, Al and Fe3+ also form the oxygen

vacancy components MgAl3+O2.5□0.5 and MgFe3+O2.5□0.5. The phase relationships of bridgmanite with coexisting phases are discussed as a function of pressure, temperature, and oxygen fugacity

from the simple MgSiO3 system to the complex MgO-Fe2+O-Fe3+2O3-Al2O3-SiO2 system. SIMILAR CONTENT BEING VIEWED BY OTHERS CALCIUM DISSOLUTION IN BRIDGMANITE IN THE EARTH’S DEEP MANTLE Article

19 October 2022 INCORPORATION MECHANISM OF FE AND AL INTO BRIDGMANITE IN A SUBDUCTING MID-OCEAN RIDGE BASALT AND ITS CRYSTAL CHEMISTRY Article Open access 24 November 2021 PRESSURE

STABILIZES FERROUS IRON IN BRIDGMANITE UNDER HYDROUS DEEP LOWER MANTLE CONDITIONS Article Open access 21 May 2024 INTRODUCTION Bridgmanite ((Mg, Fe)SiO3-Al2O3, Bdm) is the Earth’s lower

mantle’s most abundant mineral. The lower mantle extends from 660 Km to 2890 Km depth, corresponding to 23–136 GPa, and comprises 56% of Earth’s volume. The mantle’s composition is primarily

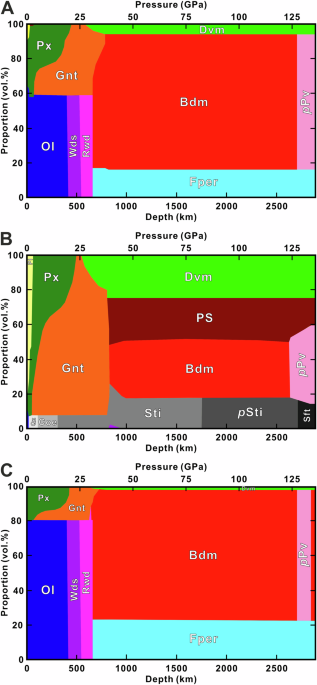
peridotitic, containing 45.0% SiO2, 37.8% MgO, 8.1% FexO, 3.6% CaO, and 4.45% Al2O3 by weight1. The lower mantle’s mineralogy consists of 80% Bdm, 15% ferropericlase ((Mg, Fe)O, Fper), and

10% of davemaoite (CaSiO3, Dvm) by volume (Fig. 1A)2. Below the D” discontinuity in high-velocity regions, postperovskite ((Mg, Fe)SiO3-Al2O3) likely replaces Bdm3. The differentiation under

mid-oceanic ridges creates oceanic plates with 18% basalt and 82% harzburgite2, which subduct into the lower mantle. The resulting basaltic domain contains 32% Bdm, 25% Dvm, 26% postspinel

phase (MgAl2O4, PS), and 18% stishovite (SiO2, Sti) (Fig. 1B), while the harzburgite domain comprises 74% Bdm, 22% Fper, and 3% Dvm (Fig. 1C)2. As the predominant mineral in all lithologies

of the lower mantle, Bdm’s phase relations with secondary minerals, _i.e_., Fper, Dvm, PS, and Sti, are crucial for understanding mantle dynamics and evolution. Bdm is named after Percy

Williams Bridgman, a pioneering American high-pressure physicist. This review examines Bdm’s phase relations with secondary phases under pressure (_P_)—temperature (_T_) conditions relevant

to Earth’s mantle. It focuses on major mantle elements (O, Si, Mg, Fe, Al, and Ca) and H, which, although not a major constituent, could significantly alter mineral properties4. This study

excludes phase relations in natural systems. Figure 1 illustrates Bdm’s predominance in the lower mantle but does not specify exact mineral proportions. Bdm phase relations are primarily

studied using laser-heated diamond anvil cells (LH-DAC) and multi-anvil presses (MAP). LH-DAC covers Bdm’s entire stability field but has significant temperature uncertainties (100–400 

K)5,6,7,8,9,10,11 and pressure uncertainties (1–5 GPa or up to 7%)6,7,9,10,11,12. It also risks chemical heterogeneity due to the Soret effect13. Sample analysis techniques have evolved from

unit cell volume estimates to transmission electron microscopy (TEM) with focused ion beam (FIB), though spatial resolution remains a challenge for very small grain sizes. Notably, silicate

samples prepared using FIB are typically more than 100 nm, and the spatial resolution of TEM analysis is comparable to the sample thickness14. On the other hand, MAP offers more precise

_P_-_T_ conditions, with temperature fluctuations of typically 5 K15,16,17,18 and pressure uncertainties of 0.05–1 GPa15,16,17,18,19. It avoids Soret effect issues. The size of recovered

samples is several hundred μm, allowing various post-analysis using multiple techniques. The phases present can be identified using a microfocused powder X-ray diffractometer (MF-XRD).

Sample textures can be observed using scanning electron microscopy (SEM) with backscattered electron imaging (BEI). The grain sizes are larger than 2-3 μm below 27 GPa and above 1700 K,

allowing for reliable compositional analysis using an electron microprobe (EPMA), whose precision is better than 0.1 wt.%20,21,22,23,24,25,26. The grain size becomes smaller with increasing

pressure but usually above several 100 nm, which allows reliable analysis using an analytical TEM with an energy-dispersive X-ray spectrometer (EDS). The determination of Fe3+/ΣFe is also

possible using Mössbauer spectroscopy with a precision of 0.02 ~ 0.0525,26,27,28,29,30. MAP’s pressure range was historically limited to 26 GPa but recently extended to 52 GPa31. This paper

reviews the experimental data obtained using MAP and LH-DAC, supplemented by ab initio calculations. CRYSTAL CHEMISTRY OF BRIDGMANITE Bdm has an orthorhombic perovskite structure (Fig. 

2A)32,33 with MgSiO3 as its principal component. In this structure, Mg2+ and Si4+ occupy the A- and B-sites, respectively, surrounded by eight~twelve and six O2− 33, expressed as

[Mg2+]A[Si4+]BO32−. Dvm also has a perovskite structure, but in cubic form34 (Fig. 2B). This difference between Bdm and Dvm is due to the ionic radii of their A-site cations: 8-coordinated

Mg2+ (89 pm) and Ca2+ (112 pm), respectively35,36. The smaller Mg2+ in Bdm causes A-site distortion and SiO6 octahedron rotation, resulting in the orthorhombic structure. In contrast, the

larger Ca2+ in Dvm allows for the cubic perovskite structure. Ionic radii of cations provide insights into Bdm chemistry. The A-site, typically occupied by 8-coordinated Mg2+, can

accommodate similarly sized cations like Fe2+ (92 pm) and Fe3+ (78 pm) in high-spin states. It doesn’t primarily accommodate larger cations like Ca2+. Al3+ (estimated 61 pm) can occupy the

A-site37, but its smaller size may explain why high pressure is needed for incorporation. The B-site, occupied by 6-coordinated Si4+ (40 pm), can only accommodate small cations. Al3+ (54 pm)

fits well, while Fe3+ (66 pm) is accommodated in limited amounts20, possibly due to its larger size. The 6-coordinated ionic radius of high-spin Fe2+ (78 pm) is likely too large for the

B-site. Note: Effective ionic radii were extrapolated from Shannon’s36 data when not explicitly given. The valence differences between Mg2+ and Si4+ (2+ and 4+ valence) and Al3+ and Fe3+ (3+

valence) lead to various substitution mechanisms in Bdm. When Al or Fe3+ occupies the A- or B-site, it is favourable for the other site to also be occupied by a trivalent cation, forming

charge-coupled (CC) components like [Al3+]A[Al3+]BO2−3 and [Fe3+]A[Fe3+]BO2−320,37. However, as the ionic radii of Al and Fe3+ are more similar to those of Si and Mg, respectively, the Fe3+

and Al cations are preferably accommodated in the A- and B-sites, respectively, forming [Fe3+]A[Al3+]BO2−321. Al and Fe3+ can also occupy the B-site even when divalent cations (Mg2+ and

Fe2+) are in the A-site. This creates oxygen vacancies (□) to balance charges, forming oxygen vacancy (OV) components like [Mg2+]A[Al3+]BO2−2.5□0.5 and [Fe2+]A[Al3+]BO2−2.5□0.538.

Conversely, when Al or Fe3+ occupies the A site with Si4+ in the B site, cation vacancies form to compensate for excess positive charge, resulting in A-site vacancy (AV) components like

[□1/3Al3+2/3]A[Si4+]BO2−3 and [□1/3Fe3+2/3]A[Si4+]BO2−320,38. Molar volume is crucial for understanding chemical changes with _P_. Table 1 shows molar volumes of various Bdm components at

ambient conditions. All secondary components have larger molar volumes than MgSiO3 (24.447(4) cm3/mol), including OV, despite their lack of oxygen. The incorporation mechanism of H+ in Bdm

is not yet fully understood until recently due to the limited H2O content. Drawing parallels from Mg2SiO4 wadsleyite, an upper mantle mineral, where H+ occupies the Mg site forming the

[Mg2+2H+]2[Si4+]O2−439, it was hypothesised that H+ might similarly occupy the Mg (A-) site in Bdm40, creating [2H+]A[Si4+]BO2−3. An alternative mechanism proposed that H+ could couple with

Al3+ to substitute Si4+ in the B-site41, forming [Mg2+]A[Al3+H+]BO2−3 A recent neutron scattering study has provided evidence supporting this latter substitution mechanism in Bdm42. The

variety of components in Bdm underscores the importance of coexisting phases in determining its chemistry. The species of coexisting phases should vary with the bulk composition. The content

of different components in Bdm varies with the coexisting phases, which in turn depend on the bulk composition. In (Mg, Fe2+)O excess or SiO2-deficient systems, OV likely forms, while in

SiO2 excess systems, AV forms38. To define a unique defect structure at a given _P_ and _T_, the Gibbs phase rule must be considered. For a system with _n_ components, _n-1_ additional

phases must coexist with Bdm. For instance, in a three-component system (MgO-Al2O3-SiO2), two additional phases besides Bdm are necessary. Many studies have not fully considered the

implication of the phase rule, often having an insufficient number of coexisting phases. While the following sections will interpret Bdm phase relations, it is important to note that this

review is not exhaustive. PHASE RELATIONS OF BRIDGMANITE IN VARIOUS SYSTEMS MGSIO3 The MgSiO3 system is fundamental for understanding Bdm stability. Figure 3 summarises Bdm’s stability

field, bounded by transitions to akimotoite (Aki) at low _P_ and _T_ 43,44,45,46,47,48,49,50,51, to postperovskite (_p_Pv) at high _P_5,52,53,54,55, and MgSiO3 melt at high _T_

56,57,58,59,60,61,62,63,64. A small region of tetragonal garnet (Gnt), often referred to as majorite, exists between Aki and melt47,56. Recent studies define these boundaries with more

precision. Figure 3 shows the most recently determined boundaries with Aki49, _p_Pv5, and melt64. The Bdm- Aki boundary has a negative slope (d_P_/d_T_), −3.2 to −8.1 MPaK−1 as _T_ decreases

from 2100 to 1250 K49 with transition _P_ at 24.0 GPa at 2100 K and 20.5 GPa at 1250 K. The Bdm-_p_Pv boundary exhibits a steep positive d_P_/d_T_ of 13.3 MPaK−1, with transition _P_ at 107

 GPa at 1500 K and 150 GPa at 4500 K35. The melting curve starts at 2700 ~ 2800 K at 22 GPa56,63, rapidly increases to 4300 K at 60 GPa, then gradually reaches 5200 K at 140 GPa64.

Extrapolation suggests a triple point (Bdm-_p_Pv-melt) at 5200 K and 160 GPa. The Bdm-Gnt boundary remains less studied. MGO-SIO2 In the MgO-rich region of the MgO-SiO2 system, Bdm coexists

with periclase (MgO, Per). The Bdm+Per field is bounded by ringwoodite (Mg2SiO4, Rwd) at low-_P_, as shown in Fig. 4A. This phase boundary, extensively studied for its geophysical importance

in relation to the 660-km seismic discontinuity, occurs at 23–24 GPa15,31,43,49,65,66,67. The Rwd to Bdm + Per transition exhibits a near-zero d_P_/d_T_ below 1700 K, becoming increasingly

negative at higher _T_, reaching −0.9 MPaK−1 at 2000 K68. Above 2500 K, Rwd transforms into wadsleyite (Mg2SiO4, Wds) following a boundary 11.0 (GPa) + 4.5 (MPaK−1) × _T_ (K)68, leading to a

transition from Bdm + Per to Wds rather than Rwd. Both Bdm + Per and Wds become melt + Per above 2500 K at 19 to 27 GPa63. On the SiO2-rich region of the MgO-SiO2 system, Bdm coexists with

SiO2 stishovite (Sti) at a relatively lower _P_. At 68-78 GPa, Sti transforms to CaCl2-type SiO2, known as post-stishovite (_p_St)6. At even higher _P_, _p_St may transform to α-PbO2-type

SiO2, called seifertite (Sft), although it is unclear if this transformation occurs within the Bdm stability field7. Thus, above 68-78 GPa, Bdm primarily coexists with _p_St. No intermediate

phases between Bdm and silica phases have been reported in the literature. The melting relations of Bdm + Per and Bdm + Sti, though not extensively studied, exhibit congruent melting69.

Figure 4B illustrates the melting relations in the MgO-SiO2 system proposed by Yao et al.69 based on multi-anvil experiments and first-principle calculations. At 24 GPa, the eutectic _T_ for

Bdm + Per and Bdm + Sti, respectively, are 2650 K63 and 2700 K69. Per and Sti have significantly higher melting _T_ (4800 and 4200 K) than Bdm (2750 K) at this _P_. Consequently, the

compositions of Bdm + Per and Bdm + Sti melts are similar to pure Bdm with MgO/(MgO+SiO2) of 0.43 and 0.53, respectively, compared to 0.5 for Bdm. As _P_ increases, the melting _T_ in the

MgO-SiO2 system rises while maintaining similar geometrical relations. At 136 GPa, the eutectic _T_ for Bdm + Per and Bdm + Sti reaches 5500 and 5400 K, respectively. As the melting

temperature differences between Bdm (5550 K) and Per (7500 K) and Sti (5900 K) decrease, the eutectic compositions of Bdm + Per and Bdm + Sti, MgO/(MgO+SiO2) = 0.35 and 0.67, respectively,

deviate more significantly from the MgSiO3 composition. MGO-FE2+O-SIO2 Following the MgO-SiO2 system, the MgO-Fe2+O-SiO2 system was initially anticipated to be the second most important

system in geophysics due to Fe’s abundance as the fourth element in Earth’s mantle1. While the majority of Earth’s Fe is stored in the liquid outer core, the deep mantle’s reducing

conditions70 led to the expectations that Fe would primarily exist in its 2+ state. However, recent studies have revealed that Fe3+ plays an even more crucial role in mantle chemistry than

Fe2+ 27,71, a topic that will be explored in later sections. The investigation of Bdm’s phase relations in this system began shortly after its discovery72, reflecting its perceived

importance in understanding Earth’s lower mantle composition and dynamics. MAXIMUM FE2+SIO3 CONTENT Fe2+ can substitute for Mg2+ in the A-site, forming Fe2+SiO373. However, there is a limit

to the maximum Fe2+SiO3 content in Bdm, denoted as \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\). When the Fe2+SiO3 content in Bdm, \({{{\rm{\chi

}}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\), exceeds this limit, Fper + Sti forms. In planets with mantles richer in Fe2+O than Earth’s, Fper + Sti could be the major mantle

phase rather than Bdm. Due to its geophysical significance, \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) has been extensively studied as a function of _T_

43,75,76,77 and _P_ 8,76,77,78. While Fe2+ undergoes a spin transition in certain minerals like Fper, at high _P_ 79, Fe2+ in the Bdm A-site remains in the high-spin state throughout its

stability field79. Consequently, the chemistry of Fe2+-bearing Bdm should change gradually or remain unaltered with _P_. Figure 5A illustrates the variation of \({\varphi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) at _ca_. 26 GPa as a function of _T_ determined using a MAP43,75,76,77. The data can be divided into two groups based on the anvil

material: tungsten carbide (WC)43,74,75 and sintered diamond (SD)76,77. Studies using WC anvils found \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) to be 7 mol.% at

1400 K, increasing to 12 mol.% at 2000 K. In contrast, studies using SD anvils reported 16 mol.% at 1800 K, rising to to 18 mol.% at 2300 K. The SD anvils results are 1.3-2.0 times higher

than WC anvil results at comparable _T_. The reason for this discrepancy is not fully understood. One possible explanation is that the actual _T_ in the WC anvil experiments may have been

higher than that in the SD anvil experiments, though this would require a difference of over 1000 K to account for this difference in \({\varphi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\). Another possibility is that extremely small grain sizes in the SD anvil experiments may have led to microprobe analyses of

bridgmanite inadvertently including more Fe-rich ferropericlase grains. Figure 5B illustrates the variation in \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) as a

function of _P_ at various _T_ using data from LH-DAC experiments8,78 and MAP with SD anvils76,77. Both data indicate that \({\varphi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) increases with _P_ at similar rates of 0.42 to 0.60 mol.%GPa−1 with no apparent effect from the Fe2+ spin transition in Fper79.

LH-DAC results show lower \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) 8,78 compared to MAP with SD anvils76,77, but are consistent with MAP using WC anvils43,74,75.

MAP with SD anvils76,77 yielded a \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) of 38 mol.% at 2000 K near 60 GPa. Dorfman et al.‘s LH-DAC study on the MgSiO3-Fe2+SiO3

system8 showed a rapid increase in \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) from 60 to 70 GPa, implying a possible formation of pure Fe2+SiO3 Bdm. However, this

drastic change is challenging to interpret thermodynamically without assuming significant changes in partial molar volumes with increasing _P_. The Sti-_p_Sti transition occurring between 58

and 78 GPa has minimal effect on phase relations due to similar volumes of these minerals6. Given the inconsistencies in the reported \({\varphi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\), a comprehensive reinvestigation is necessary. This study should cover a wide _P_-_T_ range and employ reliable experimental and

analytical techniques to establish more definitive conclusions about \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\). FE2+-MG EXCHANGE COEFFICIENT WITH FERROPERICLASE

The Fe-Mg exchange between Bdm and Fper is geophysically important, as Fper is the only ferromagnesian mineral coexisting with Bdm in Earth’s mantle. The substitution of Mg by Fe2+ notably

affects the physical properties of these minerals, altering their density and electrical conductivity6,80. The exchange coefficient of Fe2+ and Mg of Bdm with Fper,

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\), is defined as:

$${K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}=\frac{\left({{{\rm{\chi }}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}/{{{\rm{\chi

}}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\right)}{\left({{{\rm{\chi }}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}/{{{\rm{\chi

}}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}\right)}$$ (1) where χ_α__i_ is the fraction of the component _i_ in phase α. While the apparent Fe-Mg exchange coefficient is

significantly altered by Al incorporation81, making direct application to Earth’s mantle challenging, \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) in the

MgO-Fe2+O-SiO2 system remains important as a foundatioin for understanding Fe distribution in these minerals. Numerous studies have attempted to determine

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) at 23–25 GPa using MAP43,74,83,84,85. However, achieving equilibrium has been challenging. Many workers used

olivine as a starting material, but this approach led to issues with low-_T_ compositions persisting due to slow kinetics82 and Fe2+ oxidation to Fe3+ during the dissociation84. Nakajima et

al.85 provided the best understanding of \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) for the topmost lower mantle conditions. They measured compositions of

Bdm and Fper coexisting with metallic iron at significantly high _T_ (2400–2600 K) using various bulk compositions. This approach minimised Fe3+ content and allowed for chemical equilibrium

and grain growth suitable for microprobe analysis. While data from Katsura and Ito82 and Frost and Langenhorst84 generally align with Nakajima et al.’s85 findings, Katsura and Ito’s82

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) was higher, especially for low-Fe samples. This discrepancy may be due to significant Fe3+ in Bdm’s B-site,

caused by oxidation from B2O3 flux. The consistency improves for higher Fe samples because the B site’s Fe3+ capacity is limited, reducing its impact on

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\). The Fe2+-Mg exchange coefficient is directly related to the chemical potential change of the Fe2+-Mg exchange

reaction between Bdm and Fper. This reaction can be expressed as: $$\begin{array}{c}{{{\rm{MgSiO}}}}_{3}\\ {{\rm{Bdm}}}\end{array}+\begin{array}{c}{{{\rm{Fe}}}}^{2+}{{\rm{O}}}\\

{{\rm{Fper}}}\end{array}=\begin{array}{c}{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}\\ {{\rm{Bdm}}}\end{array}+\begin{array}{c}{{\rm{MgO}}}\\ {{\rm{Fper}}}\end{array}$$ (2) The conditions for

equilibrium of Eq. (1) can be written as: $${RT} \, {{\mathrm{ln}}}\,{K} \, _{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}=-\left(\Delta {H}^{0}+P\Delta

{V}^{0}{{\rm{\hbox{-}}}}T\Delta {S}^{0}\right)-{{\rm{R}}}T{\mathrm{ln}}\frac{\left({{{\rm{\gamma }}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}/{{{\rm{\gamma

}}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\right)}{\left({{{\rm{\gamma }}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}/{{{\rm{\gamma

}}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}\right)}$$ (3) where Δ_H_ 0, Δ_V_ 0, and Δ_S_ 0, respectively, are the enthalpy, volume, and entropy changes associated with the exchange

reaction in the standard state, _γ__α__i_ is the activity coefficient of the component _i_ in phase α, _R_ is the gas constant, and _T_ is the absolute temperature. Using the regular

solution model, the term of the acitivty coefficient can be expressed as: $$-{{\rm{R}}}T\,{{\mathrm{ln}}}\frac{\left({{{\rm{\gamma

}}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}/{{{\rm{\gamma }}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\right)}{\left({{{\rm{\gamma

}}}}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}/{{{\rm{\gamma }}}}_{{{\rm{Mg}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Fper}}}}\right)}=

{W}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}-{{{\rm{Mg}}}{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}(1{{{-}}}2{\chi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}) \\

{{{-}}}{W}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}-{{\rm{Mg}}}{{\rm{O}}}}^{{{\rm{Fper}}}}(1{{\rm{\hbox{-}}}}2{\chi }_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}})$$ (4) where

\({W}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}-{{{\rm{Mg}}}{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) and \({W}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}-{{\rm{Mg}}}{{\rm{O}}}}^{{{\rm{Fper}}}}\), respectively,

are the symmetric interaction parameters (Margules parameters) for Bdm and Fper. The parameters for this model, as determined by Nakajima et al.85, are given in Table 2. Figure 6A shows

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) for various \({\chi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) as a function of _T_ at 25 GPa

calculated using the above thermodynamic parameters. The graph also includes experimental data by Katsura and Ito82, Frost and Langenhorst84, and Nakajima et al.85. As expected,

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) increases with increasing _T_. For instance, at \({\chi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) of 8 mol.%, \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) is 0.19 at 1800 K, whereas it is 0.30 at

2600 K. More notably, \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) is strongly compositional dependent, decreasing with increasing Fe2+/(Fe2+ + Mg) ratio in

the system. For instance, at 2000 K, \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) is 0.32 at \({\chi

}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) of 4 mol.%. but drops to 0.16 at 16 mol.%. This compositional effect is significantly larger than the _T_ effect, primarily due to

the large \({W}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}-{{\rm{Mg}}}{{\rm{O}}}}^{{{\rm{Fper}}}}\), because \({W}_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}-{{{\rm{Mg}}}{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\)

can be assumed to be zero85. \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) has been studied at higher _P_ using LH-DAC9,78,82,86,87,88,89. Additionally,

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) can also be derived from data determining \({\varphi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\)

8,76,77,78 with _P_. However, understanding the _P_ dependence of \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) is challenging due to its complex

relationship with _T_ and compositions. Figure 6A shows \({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) from four studies with minimal variations in _T_ and

bulk compositions9,82,88,89. Two of the studies, Auzende et al.88 and Sakai et al.82, showed a negative _P_ dependence of

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\), which they attributed to the spin transition of Fper. However, Nakajima et al.85 suggested that this _P_

dependence could be interpreted without the spin transition. Given these conflicting interpretations, a comprehensive study is required to determine

\({K}_{{{\rm{F}}}{{{\rm{e}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) as a function of _P_, _T_, \({f}_{{{{\rm{O}}}}_{2}}\), and composition precisely. MGO-CAO-SIO2 Calcium is the

sixth most abundant element in Earth’s mantle1. In the lower mantle, CaO forms Dvm34. Bdm and Dvm are the two main phases in the MgO-CaO-SiO2 system. Since non-stoichiometry is not Known in

Dvm, the coexistence of Sti, Per, or other Ca-bearing phases should not affect the phase relations between Bdm and Dvm. Consequently, the binary MgSiO3-CaSiO3 system is crucial for

understanding the ternary MgO-CaO-SiO2 system. As Bdm and Dvm melt congruently90, the eutectic melting _T_ limits the stability of Bdm at high _T_ in this system. Furthermore, no phase

transition of Dvm is known within Bdm’s stability field at mantle temperatures. The maximum CaSiO3 content in Bdm, \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}\,}^{{{\rm{Bdm}}}}\), below the

eutectic point is geochemically significant due to Ca’s large ionic radius. This property allows Dvm to incorporate much larger amounts of trace elements, such as REE, U, and Th, than Bdm91.

Consequently, the presence of Dvm significantly impacts trace element profiles in the mantle. Given that CaSiO3 is relatively small compared to MgSiO3 in Earth’s mantle, it is crucial to

determine whether \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}\,}^{{{\rm{Bdm}}}}\) exceeds the mantle’s CaSiO3 content. If \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}\,}^{{{\rm{Bdm}}}}\)

surpasses 8 mol.%, it would imply that all Ca is contained in Bdm, and Dvm does not exist in the lower mantle. This determination is essential for understanding the distribution of calcium

and associated trace elements in the lower mantle. The phase relations of Bdm and Dvm in the MgSiO3-CaSiO3 system under topmost lower-mantle conditions (24 GPa) have been studied using

MAP90,92,93. Eutectic melting occurs between 2620 and 2700 K at this _P_ 90 (Fig. 7). \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) is very low, limited to 2 mol.% even at

the eutectic _T_, suggesting Dvm’s presence in the top of the lower mantle. It remains unknown whether \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) reaches 8 mol.% at higher

_P_. As the eutectic _T_ should increase with pressure, the maximum _T_ of Bdm stability may increase, potentially resulting in higher \({\varphi

}_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\). The miscibility gap between Bdm and Dvm could narrow with increasing _P_ if the partial molar volume of CaSiO3 in Bdm is smaller than

Dvm’s molar volume. In situ X-ray studies with MAP observed metastable Ca-rich Bdm formation at various _P_ and _T_, but it transformed to Bdm + Dvm at higher _T_ 19,93. The volumes of

Ca-rich Bdm were reported to be larger than Bdm + Dvm19, suggesting the miscibility gap is unlikely to narrow with increasing _P_. Recent laser-heated diamond anvil cells (LH-DAC) studies

reported the formation of Ca-rich Bdm at high _P_ and _T_ in Fe- and Al-bearing systems11,94. Reference 12 suggested that the secondary components of Fe and Al promoted \({\varphi

}_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}\,}^{{{\rm{Bdm}}}}\). It is noted that, however, Raoult’s law implies that the presence of minor components does not significantly alter the thermodynamic

properties of the major component. Further investigation is necessary to reach conclusive results about \({\varphi }_{{{\rm{Ca}}}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}\) at higher _P_.

MGO-AL2O3-SIO2 Al is the sixth most abundant element in the Earth’s mantle1. Significant quantities of Al2O3 can be present in Bdm, depending on prevailing conditions. Extensive research has

been conducted on the phase relations in the MgO-Al2O3-SiO2 system16,22,23,95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110. Figure 8A illustrates the phase assemblage in this

system at 27 GPa and 2000 K38. As the Mg/Si ratio decreases from infinite to zero, the phases coexisting with Bdm change from Per, Per + PS111,112, PS, PS + corundum (Crn), Crn, Crn + Sti,

and Sti. This PS has a CaFe2O4-structure111, with MgAl2O4 as its primary component, but can contain Mg2SiO4113. Similarly, Crn’s primary component is Al2O3, but it can contain

MgSiO337,98,100,114. At these conditions, the Mg2SiO4 and MgSiO3 contents in CaFe2O4-type PS and Crn coexisting with Bdm are 29-34 and 19-21 mol.%, respectively38. The Al2O3 contents in Per

and Sti coexisting with Bdm are limited to 0.5 and 5 mol.%, respectively. Notably, the Al2O3 content in Sti may be attributed to H2O potential incorporation through the substitution Si4+ ↔ 

Al3+ + H+ 42. Al is primarily incorporated into Bdm as CC, Al2O3, especially when the Mg/Si ratio is unity, where the coexisting phase is Crn22,37,98,100,102,106,114,115. The maximum Al2O3

CC content in Bdm, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\), increases with _P_ 37,98,100,102,114,115 (Fig. 8B). For example, \({\varphi

}_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases from 12 to 22 mol.% as _P_ rises from 27 to 42 GPa at 2000 K114. Notably, when the \({\varphi

}_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) is high (at least 25 mol.%), Bdm cannot be recovered to ambient conditions but transforms to the LiNbO3 structure upon decompression109,114.

The increase in \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) with _P_ is associated with a decrease in the maximum MgSiO3 content in Crn, \({\varphi

}_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Crn}}}}\). For instance, \({\varphi }_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Crn}}}}\) decreases from 32 to 22 mol.% as _P_ rises from 27 to 35 GPa

at 2300 K. Similarly, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases with _T_ 22,37,114. For instance, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\)

increases from 16 to 30 mol.% as _T_ rises from 1700 to 3000 K at 27 GPa. This increase is accompanied by a corresponding increase in \({\varphi

}_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Crn}}}}\). The stability field of Bdm + Crn in the MgSiO3-Al2O3 system is constrained on the lower _P_ side by the formation of pyrope

Gnt16,98,100,101 at 26 GPa (Fig. 8C). The boundary in the _P_-_T_ space is curved. The d_P_/d_T_ is negative, with a value of −1.5 MPaK−1 at 1400–1800 K. At higher _T_ up to 1900–2100 K,

d_P_/d_T_ becomes positive, reaching a value of +2.5 MPaK−1. At high _P_, _ca_. 100 GPa, Crn first transforms to the Rh2O3(II) structure116. The melting relations in the Bdm + Crn system

have not yet been investigated. In MgO-rich or SiO2-poor systems, Bdm contains OV, MgAlO2.5, in addition to CC103,107,110,117,118,119. The maximum OV content, \({\varphi

}_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\), is considerably more limited than \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\)103,110,118,119. \({\varphi

}_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) rapidly decreases with _P_110, as shown in Fig. 8D. For instance, \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) decreases from

6 to 1 mol.% as _P_ rises from 27 to 40 GPa at 2000 K when coexisting with Per. The _T_ dependence of \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) varies based on the

coexisting phases (Fig. 8E)119. When Bdm coexists with Per and Per + PS, respectively, \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases from 3 to 6 mol.% and from 3 to 4

 mol.%, respectively, as _T_ rises from 1700 to 2300 K. However, when coexisting with PS + Crn, \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) decreases from 4 to 3 mol.% as _T_

rises from 2000 to 2300 K23. Generally, the _T_ dependence of \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) decreases with increasing the Al2O3 content, _i.e._, in the order

of Per → Per + PS → PS + Crn. The local chemical environment of Al3+ in OV is complex. Nuclear magnetic resonance (NMR) studies have indicated that Al3+ in Bdm can have coordination numbers

of 4, 5, 6, and 829,120,121. Among these, 6-coordinated Al3+ are predominant, suggesting a random distribution of Al3+ and O2− vacancies. However, the presence of 4-coordinated Al3+

indicates the formation of clusters comprising both Al3+ and O2− vacancies. The variation in the OV content, \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\), is more complex than

\({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\). When the bulk Al2O3 content in Bdm, \({\chi }_{{{{\rm{Al}}}}_{2}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}={\chi

}_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}+0.5{\chi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\), increases to approximately 10 mol.% in the presence of Per, the \({\chi

}_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) initially increases and then decreases at \({\chi }_{{{{\rm{Al}}}}_{2}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}\). In contrast, \({\chi

}_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases monotonically (Fig. 8F). Huang et al.81 employed a thermodynamic approach to express the equilibrium of Bdm and Per in the

MgO-Al2O3-SiO2 system. To address the complexity of OV, they introduced the \({{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\rm{\square

}}}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}\) component instead of MgAlO2.5. This equilibrium was represented by the following equation:

$$\begin{array}{c}{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square }}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}\\

{{\rm{Brg}}}\end{array}=\frac{1}{16}\begin{array}{c}{{{\rm{AlAlO}}}}_{3}\\ {{\rm{Brg}}}\end{array}+\frac{7}{8}\begin{array}{c}{{{\rm{MgSiO}}}}_{3}\\

{{\rm{Brg}}}\end{array}+\frac{1}{8}\begin{array}{c}{{\rm{MgO}}}\\ {{\rm{Per}}}\end{array}$$ (5) The standard Gibbs energy of reaction (5) at equilibrium, Δ_G_(5)0, was expressed using the

following equation: $$\Delta

{G}_{\left(5\right)}^{0}=-{{\rm{R}}}T\,{{\mathrm{ln}}}\frac{{\left({a}_{{{{\rm{AlAlO}}}}_{3}}^{{{\rm{Bdm}}}}\right)}^{\frac{1}{16}}{\left({a}_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}\right)}^{\frac{7}{8}}{\left({a}_{{{\rm{MgO}}}}^{{{\rm{Per}}}}\right)}^{\frac{1}{8}}}{{a}_{{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square

}}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}}^{{{\rm{Bdm}}}}}$$ (6) where _a_A_i_ is the activity of component _i_ in phase A. To consider the fraction of

\({{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square }}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}\), \({\chi

}_{{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\rm{\square }}}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}}^{{{\rm{Bdm}}}}\), they assumed that O2− vacancies

occur on the O1 site (multiplicity of unity) and not on the O2 site (multiplicity of two). This results in: $${\chi

}_{{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square

}}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}}^{{{\rm{Bdm}}}}=1.841{x}_{{{{\rm{Mg}}}}_{{{\rm{A}}}}}^{{{\rm{Bdm}}}}{\left({x}_{{{{\rm{Al}}}}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\right)}^{\frac{1}{8}}{\left({x}_{{{{\rm{Si}}}}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\right)}^{\frac{7}{8}}{\left({x}_{{{{\square

}}}_{{{\rm{O}}}1}}^{{{\rm{Bdm}}}}\right)}^{\frac{1}{16}}{\left({x}_{{{{\rm{O}}}}_{{{\rm{O}}}1}}^{{{\rm{Bdm}}}}\right)}^{\frac{15}{16}}$$ (7) where

\({x}_{{{{\rm{Mg}}}}_{{{\rm{A}}}}}^{{{\rm{Bdm}}}}\), \({x}_{{{{\rm{Al}}}}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\), and \({x}_{{{{\rm{Si}}}}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\) are the fractions of Mg on

the A site, Al and Si on the B site, respectively, and \({x}_{{{{\rm{\square }}}}_{{{\rm{O}}}1}}^{{{\rm{Bdm}}}}\) and \({x}_{{{{\rm{O}}}}_{{{\rm{O}}}1}}^{{{\rm{Bdm}}}}\) are the fractions of

vacancies and oxygen on the O1 site, respectively. The coefficient 1.841 ensures that the activity of the endmember MgSi7/8Al1/8O15/16□1/16O2 equals unity and is driven from

\(1/{\left(\frac{1}{8}\right)}^{\frac{1}{8}}{\left(\frac{7}{8}\right)}^{\frac{7}{8}}{\left(\frac{1}{16}\right)}^{\frac{1}{16}}{\left(\frac{15}{16}\right)}^{\frac{15}{16}}\). The MgSiO3

fraction in Bdm, \({\chi }_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}\), was expressed as follows: $${\chi

}_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}={x}_{{{\rm{Mg}}},{{\rm{A}}}}^{{{\rm{Bdm}}}}{x}_{{{\rm{Si}}},{{\rm{B}}}}^{{{\rm{Bdm}}}}{x}_{{{\rm{O}}},{{\rm{O}}}1}^{{{\rm{Bdm}}}}$$ (8) The

regular symmetric solution model was used to express the activity coefficient of MgSi7/8Al1/8O15/16□1/16O2, \({\gamma

}_{{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square }}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}}^{{{\rm{Bdm}}}}\): $${{\rm{R}}}T\,{{\mathrm{ln}}}{\gamma

}_{{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Al}}}}_{\frac{1}{8}}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square }}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}}^{{{\rm{Bdm}}}}=

{W}_{{{\rm{Mg}}}-{{\rm{Al}}},{{\rm{A}}}}^{{{\rm{Bdm}}}}{\left(1-{x}_{{{\rm{Mg}}},{{\rm{A}}}}^{{{\rm{Bdm}}}}\right)}^{2}+{W}_{{{\rm{Al}}}-{{\rm{Si}}},{{\rm{B}}}}{\left(1-{x}_{{{\rm{Al}}},{{\rm{B}}}}^{{{\rm{Bdm}}}}\right)}^{2}

\\ +{W}_{{{\rm{O}}}-{{\square }},{{\rm{O}}}1}^{{{\rm{Bdm}}}}{\left(1-{x}_{{{\square }},{{\rm{O}}}1}^{{{\rm{Bdm}}}}\right)}^{2}$$ (9) where _W_Bdm_i_-_j_,_α_ are the interaction parameters

between components _i_ and _j_ in the _α_ site in Bdm. Similar expressions were provided for the activity coefficients of MgSiO3 and AlAlO3: $${{\rm{R}}}T\,{{\mathrm{ln}}}{\gamma

}_{{{\rm{MgSi}}}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}={W}_{{{\rm{Al}}}-{{\rm{Si}}},{{\rm{B}}}}^{{{\rm{Bdm}}}}{\left(1-{x}_{{{\rm{Si}}}{,}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\right)}^{2}$$ (10)

$${{\rm{R}}}T\,{{\mathrm{ln}}}{\gamma

}_{{{{\rm{Al}}}}_{2}{{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}={W}_{{{\rm{Al}}}-{{\rm{Si}}},{{\rm{B}}}}^{{{\rm{Bdm}}}}{\left(1-{x}_{{{{\rm{Al}}}}_{{{\rm{B}}}}}^{{{\rm{Bdm}}}}\right)}^{2}$$ (11) The

parameters evaluated by Huang et al.81 are presented in Table 3. This formulation and the estimated parameters provide a comprehensive description of \({\chi

}_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) and \({\chi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) in relation to \({\chi

}_{{{{\rm{Al}}}}_{2}{{{\rm{O}}}}_{3}{{\rm{m}}}}^{{{\rm{Bdm}}}}\), as illustrated in Fig. 8F. MGO-FE3+ 2O3-SIO2 Despite Fe being the fourth most abundant element in Earth’s mantle1, Fe3+ was

previously thought to play a minor role in the lower mantle. This assumption was based on the presumed reducing conditions of the lower mantle, inferred from its contact with the outer core.

As a result, phase relations in the MgO-Fe3+2O3-SiO2 system have not been extensively studied. Another factor contributing to the limited study on this system is the difficulty in

maintaining and accurately measuring Fe valence during and after high _P_-_T_ experiments, making it challenging to obtain reliable data on Fe3+ behaviour under lower-mantle conditions. The

phase relations in the MgO-Fe3+2O3-SiO2 system are similar to those in the MgO-Al2O3-SiO2 system20,30,122,123. Fe3+ can occupy the A- and B-sites, like Al3+. However, the coexisting phases

with Bdm have not been precisely determined as a function of the Mg/Fe3+/Si ratio. As the Mg/Fe3+ ratio decreases at Mg/Si ratios less than 1:1, the coexisting phases change from Per, Per +

PS, and PS,20,122,123 (Fig. 9). This PS has a MgFe2O4 composition and a CaMn2O4 structure. At Mg/Si ratios greater than 1:1, Bdm coexists with Sti and an unidentified phase with a LiNbO3

structure after recovery30. This phase has a composition of approximately Mg/Si = 1:1 and MgSiO3/Fe2O3 = 1:2 at 27 GPa and 1700 to 2000 K. It is possible that this LiNbO3-structured phase

may also have a perovskite structure at high pressure, suggesting a potential miscibility gap in perovskite phases within the MgSiO3-Fe2O3 system. At Mg/Si ≈ 1, Bdm or the LiNbO3-structured

phase should coexist with a Fe2O3 polymorph. Although numerous Fe2O3 polymorphs exist124, it is unclear which one coexists with Bdm under specific _P_-_T_ conditions. Bykova et al.124

proposed a series of phase transitions for Fe2O3 with _P_: α-phase (hematite, Hem) → ι-phase (Rh2O3(II) structure) at 25-45 GPa → ζphase (distorted perovskite structure) at 45-55 GPa →

η-phase (CaIrO3 structure). The incorporation of Fe3+ is more limited than that of Al3+. While the maximum Fe3+ CC content in Bdm, \({\varphi

}_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\), coexisting with Fe2O3 phases has not been studied, research on \({\varphi }_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) in

other systems suggests its comparable significance at top lower mantle _P_. For instance, \({\varphi }_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) increases from 2 to 8 mol.% as

_T_ rises from 1700 to 2300 K when coexisting with Per and PS at 27 GPa20, which is a similar increases in \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) from 4 to 7 mol.% under

the same conditions119 (Fig. 9B). _P_ appears to have contrasting effects on \({\varphi }_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) and \({\varphi

}_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\). As _P_ rises from 27 to 40 GPa at 2300 K, \({\varphi }_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) decreases from 8 to 5 mol.%

when coexisting with Per and PS123. Conversely, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases from 12 to 22 mol.% as _P_ increases from 27 to 42 GPa at 2000 K when

coexisting with Crn114. It should be noted, however, that these two data sets cannot be directly compared due to the difference in the coexisting phase. Unlike Fe3+ CC, the Fe3+ OV

component, MgFe3+O2.5□0.5, is more limited compared to its Al counterpart, MgAlO2.5□0.5. When coexisting with Per and PS, \({\varphi }_{{{{\rm{OV}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\)

remains around 2 mol.% between 1700 and 2300 K at 27 GPa20 (Fig. 9B). Contrastly, \({\varphi }_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) increases from 3 to 4 mol.% under similar

conditions119. The formation of both Fe3+ and Al OV is inhibited by _P_, which is more profound for Fe3+. As _P_ rises from 27 to 40 GPa at 2300 K, \({\varphi

}_{{{{\rm{OV}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) decreases from 3 to 0 mol.%, showing a more significant reduction compared to \({\varphi

}_{{{{\rm{OV}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) (Fig. 8D). Huang et al.81 extended their thermodynamic approach from the Mg-Al-Si-O system to investigate the phase equilibrium of Bdm

coexisting with Fper in the Mg-Fe3+-Si-O system. They proposed a reaction similar to Eq. (5):

$$\begin{array}{c}{{{\rm{MgSi}}}}_{\frac{7}{8}}{{{\rm{Fe}}}}_{\frac{1}{8}}^{3+}{{{\rm{O}}}}_{\frac{15}{16}}{{{\square }}}_{\frac{1}{16}}{{{\rm{O}}}}_{2}\\

{{\rm{Bdm}}}\end{array}=\frac{1}{16}\begin{array}{c}{{{{\rm{Fe}}}}^{3+}{{{\rm{Fe}}}}^{3+}{{\rm{O}}}}_{3}\\ {{\rm{Bdm}}}\end{array}+\frac{7}{8}\begin{array}{c}{{{\rm{MgSiO}}}}_{3}\\

{{\rm{Bdm}}}\end{array}+\frac{1}{8}\begin{array}{c}{{\rm{MgO}}}\\ {{\rm{Per}}}\end{array}$$ (12) Thermodynamic parameters for this model were suggested (as listed in Table 4). However, the

model’s accuracy in reproducing experimental data is unsatisfactory. This imprecision likely stems from the limited number of experiments conducted on this system and the potential for Fe3+

to be reduced to Fe2+ during experiments. MGO-FEALO3-SIO2 Due to the similarity in ionic radii between Fe3+ and Al and between Mg and Si, it is expected that the Fe3+ and Al would

predominantly occupy the A- and B-sites, respectively125. This expectation has been confirmed by single-crystal X-ray diffraction125. Notably, even under reduced conditions, Fe in Fe,

Al-bearing Bdm remains predominantly Fe3+ through coupling with Al27,71. This coupling is thought to promote the formation of CC of FeAlO3 while inhibiting OV. Consequently, the maximum CC

fraction of FeAlO3, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{FeAl}}}}}^{{{\rm{Bdm}}}}\), is much larger than \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{Al}}}}}^{{{\rm{Bdm}}}}\) and \({\varphi

}_{{{{\rm{CC}}}}_{{{{\rm{Fe}}}}^{3+}}}^{{{\rm{Bdm}}}}\) 21,126,127. At 27 GPa and 2000 K, \({\varphi }_{{{{\rm{CC}}}}_{{{\rm{FeAl}}}}}^{{{\rm{Bdm}}}}\) reaches 67 mol.%, when Bdm coexists

with Crn and Hem. Notably, Bdm with \({\chi }_{{{{\rm{CC}}}}_{{{\rm{FeAl}}}}}^{{{\rm{Bdm}}}}\) exceeding 40 mol.% transforms to the LiNbO3 structure upon decompression21,24, similar to

Al2O3-rich Bdm109,114. When the Fe and Al contents are equal, the OV content is virtually zero25,125. A small quantity of MgAlO2.5□0.5 is observed when the Al content exceeds the Fe

content125. While the phase relations in the MgO-FeAlO3-SiO2 remain largely unexplored, those in the MgO-FeAlO3-MgSiO3 system were studied at 1700–2300 K at 27 GPa25. Under these conditions,

Bdm coexisted with PS, primarily composed of MgAl2O4 and MgFe2O4 (likely with a CaTi2O4-type structure), and minor Crn. Bdm’s main composition was 28–32 mol.% MgSiO3, 65–68 mol.% FeAlO3

with minor Fe2O3. The formation of Crn and the incorporation of Fe2O3 in Bdm suggest that Bdm favours Fe2O3 over Al2O3. Despite a slight increase in FeAlO3 with rising _T_, no significant

compositional changes were observed across the _T_ range. MGO-FEO-FE2O3-AL2O3-SIO2 This system is most relevant for understanding Bdm chemistry in the lower mantle. However, its complexity,

with five components, makes comprehending phase relations extremely challenging. The difficulty in directly controlling the Fe3+/ΣFe ratio further complicates investigations. Some studies

assume that the initial Fe3+/ΣFe in starting materials remains unchanged during a high _P_-_T_ experiment in LH-DAC experiments12. This assumption is quite questionable, especially at high

_T_ due to diffusion13. Indeed, measurements of Fe3+/ΣFe in Bdm have yielded inconsistent results across various studies12,13,128,129,130,131, suggesting that bulk Fe3+/ΣFe likely changes

during high _P_-_T_ experiments. In contrast to the conventional approach of maintaining constant bulk Fe3+/ΣFe, some studies have estimated \({f}_{{{{\rm{O}}}}_{2}}\) based on the

equilibrium between Fe-bearing phases with different valence states in the run products79,81. Specifically, \({f}_{{{{\rm{O}}}}_{2}}\) is estimated using the reaction between Fe-bearing

alloy and ferropericlase: $$2 \begin{array}{c}{{\rm{Fe}}} \\ {{\rm{alloy}}}\end{array}+{{{\rm{O}}}}_{2} = 2 \begin{array}{c}{{\rm{FeO}}} \\ {{\rm{Fper}}}\end{array}$$ (13) To produce an

alloy, a platinum group metal, typically Ir, is added, as it is not incorporated into the silicate or oxide phase. Using reaction (13), \({f}_{{{{\rm{O}}}}_{2}}\) is calculated with the

following equation: $$\log {f}_{\!\!{{\mbox{O}}}_{2}}= \frac{2{\mu }_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}}-\,2{\mu

}_{{{\rm{Fe}}}}^{{{\rm{alloy}}}}}{{{\mathrm{ln}}}10{{\rm{R}}}T}=\frac{\Delta {G}_{P,T(13)}^{0}}{{{\mathrm{ln}}}10{{\rm{R}}}T}+2\log \left({\gamma

}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}}{\chi }_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}}\right) \\ -2\log \left({\gamma }_{{{\rm{Fe}}}}^{{{\rm{alloy}}}}{\chi

}_{{{\rm{Fe}}}}^{{{\rm{alloy}}}}\right)$$ (14) The phase relations of Bdm and Fper in the MgO-FeO-Fe2O3-Al2O3-SiO2 are described based on Wang et al.26. The two exchange coefficients are

defined as follows: $${K}_{{{{\rm{Fe}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}=\frac{\frac{{\chi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}}}{{\chi

}_{{{{\rm{MgSiO}}}}_{3}}^{{{\rm{Bdm}}}} \, + \, {\chi }_{{{{\rm{Mg}}}{{\rm{Al}}}{{\rm{O}}}}_{2.5}{{{\square }}}_{0.5}}^{{{\rm{Bdm}}}}}}{\frac{{\chi

}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}}}{{\chi }_{{{\rm{Mg}}}{{\rm{O}}}}^{{{\rm{Fper}}}}}}$$ (15) $${K}_{\Sigma

{{\rm{Fe}}}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}=\frac{\frac{{\chi }_{{{{\rm{Fe}}}}^{2+}{{{\rm{SiO}}}}_{3}}^{{{\rm{Bdm}}}} \, + \, 2{\chi

}_{{{{{\rm{Fe}}}}^{3+}{{{\rm{Fe}}}}^{3+}{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}} \, + \, {\chi }_{{{{{\rm{Fe}}}}^{3+}{{\rm{Al}}}{{\rm{O}}}}_{3}}^{{{\rm{Bdm}}}}}{{\chi

}_{{{{\rm{MgSiO}}}}_{3}}^{{{\rm{Bdm}}}} \, + \, {\chi }_{{{{\rm{Mg}}}{{\rm{Al}}}{{\rm{O}}}}_{2.5}{{{\square }}}_{0.5}}^{{{\rm{Bdm}}}}}}{\frac{{\chi

}_{{{{\rm{Fe}}}}^{2+}{{\rm{O}}}}^{{{\rm{Fper}}}}}{{\chi }_{{{\rm{Mg}}}{{\rm{O}}}}^{{{\rm{Fper}}}}}}$$ (16) Unlike the previous definition of

\({K}_{{{{\rm{Fe}}}}^{2+}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\), Eq. (15) includes \({\chi }_{{{{\rm{Mg}}}{{\rm{Al}}}{{\rm{O}}}}_{2.5}{{{\square }}}_{0.5},{{\rm{Bdm}}}}\) to account

for all Mg. \({K}_{\Sigma {{\rm{Fe}}}-{{\rm{Mg}}}}^{{{\rm{Bdm}}}-{{\rm{Fper}}}}\) is referred to as the “apparent” exchange coefficient, incorporating both Fe2+ and Fe3+27,81,84,85. This

value is obtained by electron microprobe analysis without distinguishing Fe2+ and Fe3+. Wang et al.26 described the equilibrium of Bdm and Fper in the current system using the following

reactions in addition to reaction (2): $$2\begin{array}{c}{{\rm{Mg}}}{{\rm{Al}}}\left[{{{\rm{O}}}}_{0.5}{{{\square }}}_{0.5}\right]{{{\rm{O}}}}_{2}\\

{{\rm{Bdm}}}\end{array}=\begin{array}{c}{{\rm{AlAl}}}\left[{{\rm{O}}}\right]{{{\rm{O}}}}_{2}\\ {{\rm{Bdm}}}\end{array}+2\begin{array}{c}{{\rm{MgO}}}\\ {{\rm{FPer}}}\end{array}$$ (17)

$$2\begin{array}{c}{{{\rm{Fe}}}}^{2+}{{\rm{O}}}\\ {{\rm{FPer}}}\end{array}+0.5{{{\rm{O}}}}_{2}=\begin{array}{c}{{{\rm{Fe}}}}^{3+}{{{\rm{Fe}}}}^{3+}{{{\rm{O}}}}_{3}\\

{{\rm{Bdm}}}\end{array}$$ (18) $$\begin{array}{c}{{{\rm{Fe}}}}^{3+}{{{\rm{Fe}}}}^{3+}{{{\rm{O}}}}_{3}\\ {{\rm{Bdm}}}\end{array}+\begin{array}{c}{{\rm{AlAl}}}{{{\rm{O}}}}_{3}\\

{{\rm{Bdm}}}\end{array}=2\begin{array}{c}{{\rm{Al}}}{{{\rm{Fe}}}}^{3+}{{{\rm{O}}}}_{3}\\ {{\rm{Bdm}}}\end{array}$$ (19) The thermodynamics framework, based on the work of Stixrude and

Lithgow-Bertelloni132,133, begins with the following expression for the Helmholtz energy, _F_, of the endmembers: $$F\left(V,{T}_{1}\right)= \,

F\left({V}_{0},{T}_{0}\right)+\frac{9{\!V}_{\!\!0}{K}_{T0}}{2}{f}_{{{\rm{E}}}}^{2}+\frac{9{V}_{\!\!0}{K}_{T0}\left({K}_{T0}^{{\prime} }-4\right)}{2}{f}_{{{\rm{E}}}}^{3} \\

+9n{{{\rm{k}}}}_{{{\rm{B}}}}\left[{T}_{1}D\left(\frac{\theta }{{T}_{1}}\right)-{T}_{0}D\left(\frac{\theta }{{T}_{0}}\right)\right] \\

+\left[{F}_{{{\rm{mag}}}}\left({V}_{\!0},{T}_{1}\right)-{F}_{{{\rm{mag}}}}\left({V}_{\!0},{T}_{0}\right)\right]$$ (20) where K_T_0 and K_T_0’ are the bulk modulus and its pressure

derivative, _f_E is the Murnaghan’s finite stran134, kB is the Boltzmann constant, _θ_ is the Debye temperature, _D_ is the Debye function135, and _F_mag is the magnetic contribution of iron

to _F_. Wang et al.26 applied a symmetric regular solution model to determine Bdm and Fper compositions. The parameters provided are presented in Tables 5 and 6. We can obtain various

insights about Brm and Fper’s chemistry from the above formula and parameters. To show some examples, I have simulated the various contents in Bdm and Fper and the exchange coefficients in a

bulk composition similar to pyrolite by varying, \({f}_{{{{\rm{O}}}}_{2}}\), _T_, _P_, Fe/Mg, and Al/Si, whose results are given in the supplementary information. The most important insight

from these investigations is that Bdm Fe3+/ΣFe is non-zero but is several-tenths even at \({f}_{{{{\rm{O}}}}_{2}}\) below the IW buffer (Fig. S1A). Bdm Fe3+/ΣFe particularly increases from

less than 0.1 to about 0.6 as rising Al/Si from 0 to 0.3, indicating that the Fe3+ content is due to the coupling of Fe3+ and Al, especially the high stability of [Fe3+]A[Al3+]BO2−3 (Fig. 

S1I). From an Earth science perspective, this property of Bdm results in the disproportionation of Fe2+ into Fe0 and Fe3+136. $$3{{\rm{FeO}}}={{\rm{Fe}}}+{{{\rm{Fe}}}}_{2}{{{\rm{O}}}}_{3}$$

(21) In peridotite systems, this disproportionation involves Fper: $$3\begin{array}{c}{{{\rm{Fe}}}}^{2+}{{\rm{O}}}\\ {{\rm{Fper}}}\end{array}+\begin{array}{c}{{\rm{AlAl}}}{{{\rm{O}}}}_{3}\\

{{\rm{Bdm}}}\end{array}={{\rm{Fe}}}+2\begin{array}{c}{{\rm{Al}}}{{{\rm{Fe}}}}^{3+}{{{\rm{O}}}}_{3}\\ {{\rm{Bdm}}}\end{array}$$ (22) While Fe3+/ΣFe observed in upper-mantle rocks is only

about 0.04137, Bdm constitutes 80% of pyrolite with Bdm Fe3+/ΣFe of several tenths at various _P_, _T_ and _f_O2 (Fig. S1A, C, E). Consequently, free metallic iron is likely present in the

lower mantle136,137. H2O BEARING SYSTEMS Many studies have been conducted to determine the maximum H2O content in Bdm, \({\varphi

}_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\)138,139,140,141,142,143,144,145,146,147,148. As excess H2O coexisting with silicate forms a hydrous melt under mantle conditions, the

coexistence with hydrous melt is essential for determining \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\). A challenge in determining \({\varphi

}_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) is the potential presence of hydrous mineral inclusions140. As \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) is typically

minimal, such inclusions can lead to erroneous interpretation of \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\). \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) in

MgSiO3 Bdm was first reported by Meade et al.138 as 60–70 wt. ppm, using a 200 μm single crystal synthesised by Ito and Weidner149. Litasov et al.141 later reported 100 wt. ppm H2O, but

their smaller crystal size (100 μm) may have led to the broadband signals from the grain boundary rather than the crystal interior. The sharp peaks in their study indicated only 40 wt. ppm

H2O. In contrast, Bolfan-Casanova et al.140 detected only 1 ~ 2 wt. ppm H2O, suggesting that higher reported \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) might be due to

inclusions. Recently, Liu et al.145 measured \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) using a large (300 μm) single crystal and reported that it is less than 50 wt. ppm.

Considering these studies, \({\varphi }_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) in MgSiO3 Bdm is likely low, at most 50 wt. ppm. Several studies showed \({\varphi

}_{{{{\rm{H}}}}_{2}{{\rm{O}}}}^{{{\rm{Bdm}}}}\) in Fe, Al-bearing Bdm is significantly higher than in pure MgSiO3 Bdm140,141,144,146. This is attributed to the coupling of H+ with Al3+ to

substitute Si4+ in the B-site, forming [Mg2+]A[Al3+H+]BO2−42. The majority of studies42,141,142,144 reported relatively high values, such as 1000 wt. ppm H2O in Fe, Al-bearing Bdm, although

Liu et al. reported only 10~30 wt. ppm H2O. OUTLOOK Determining Bdm chemistry with high reliability is crucial, as it is the most abundant mineral in Earth’s interior. Two high _P_-_T_

apparatuses are commonly used for studying Bdm chemistry: LH-DAC and MAP. Each has its limitations: LH-DAC can cover the entire _P_-_T_ range of the lower mantle but produces less reliable

results, while MAP yields more reliable results but has limited _P_-_T_ coverage. To address these issues, efforts should focus on improving the reliability of LH-DAC experiments and

extending the _P_-_T_ range of MAP experiments. It is recommended that future studies investigate the compositions of Bdm coexisting with Fper in the MgO-FeO-Fe2O3-Al2O3-SiO2 system as a

function of pressure at Known \({f}_{{{{\rm{O}}}}_{2}}\) using these advanced experimental techniques. REFERENCES * McDonough, W. F. & Sun, S. S. The composition of the Earth. _Chem.

Geol._ 120, 223–253 (1995). Article  CAS  Google Scholar  * Stixrude, L. & Lithgow-Bertelloni, C. Geophysics of chemical heterogeneity in the mantle. In: Jeanloz, R. (Ed.), _Ann. Rev.

Earth Planet. Sci_. 40, 569–595 (2012). * Murakami, M., Hirose, K., Kawamura, K., Sata, N. & Ohishi, Y. Postperovskite phase transition in MgSiO3. _Science_ 304, 855–858 (2004). Article

  CAS  PubMed  Google Scholar  * Zhang, B. H. & Xia, Q. K. Influence of water on the physical properties of olivine, wadsleyite, and ringwoodite. _Eur. J. Mineral._ 33, 39–75 (2021).

Article  Google Scholar  * Tateno, S., Hirose, K., Sata, N. & Ohishi, Y. Determination of postperovskite phase transition boundary up to 4400 K and implications for thermal structure in

D “layer. _Earth Planet. Sci. Lett_. 277, 130–136 (2009). * Fischer, R. A. et al. Equations of state and phase boundary for stishovite and CaCl2-type SiO2. _Am. Miner._ 103, 792–802 (2018).

Article  Google Scholar  * Murakami, M., Hirose, K., Ono, S. & Ohishi, Y. Stability of CaCl2-type and α-PbO2-type SiO2 at high pressure and temperature determined by in-situ X-ray

measurements. _Geophys. Res. Lett._ 30, 1207 (2003). Article  Google Scholar  * Dorfman, S. M., Meng, Y., Prakapenka, V. B. & Duffy, T. S. Effects of Fe-enrichment on the equation of

state and stability of (Mg,Fe)SiO3 perovskite. _Earth Planet. Sci. Lett._ 361, 249–257 (2013). Article  CAS  Google Scholar  * Kobayashi, Y. et al. Fe-Mg partitioning between (Mg, Fe)SiO3

postperovskite, perovskite, and magnesiowustite in the Earth’s lower mantle. _Geophys. Res. Lett._ 32, L19301 (2005). Article  Google Scholar  * Sakai, T. et al. Fe-Mg partitioning between

perovskite and ferropericlase in the lower mantle. _Am. Miner._ 94, 921–925 (2009). Article  CAS  Google Scholar  * Ko, B. et al. Calcium dissolution in bridgmanite in the Earth’s deep

mantle. _Nature_ 611, 88–92 (2022). Article  CAS  PubMed  Google Scholar  * Shim, S. H. et al. Stability of ferrous-iron-rich bridgmanite under reducing midmantle conditions. _Proc. Natl.

Acad. Sci. USA._ 114, 6468–6473 (2017). Article  CAS  PubMed  PubMed Central  Google Scholar  * Sinmyo, R. & Hirose, K. The Soret diffusion in laser-heated diamond-anvil cell. _Phys.

Earth Planet. Inter._ 180, 172–178 (2010). Article  CAS  Google Scholar  * Moy, A., Fournelle, J. H. & von der Handt, A. Solving the iron quantification problem in low-kV EPMA: an

essential step toward improved analytical spatial resolution in electron probe microanalysis-Olivines. _Am. Miner._ 104, 1131–1142 (2019). Article  Google Scholar  * Katsura, T. et al.

Post-spinel transition in Mg2SiO4 determined by high _P_-_T_ in situ X-ray diffractometry. _Phys. Earth Planet. Inter._ 136, 11–24 (2003). Article  CAS  Google Scholar  * Ishii, T. et al.

Buoyancy of slabs and plumes enhanced by curved post-garnet phase boundary. _Nat. Geosci._ 16, 828–832 (2023). Article  CAS  Google Scholar  * Ishii, T. et al. Complete agreement of the

post-spinel transition with the 660-km seismic discontinuity. _Sci. Rep._ 8, 6358 (2018). Article  PubMed  PubMed Central  Google Scholar  * Ishii, T. et al. Sharp 660-km discontinuity

controlled by extremely narrow binary post-spinel transition. _Nat. Geosci_. https://doi.org/10.1038/s41561-019-0452-1 (2019). * Asahara, Y. et al. Formation of metastable cubic-perovskite

in high-pressure phase transformation of Ca(Mg, Fe, Al)Si2O6. _Am. Miner._ 90, 457–462 (2005). Article  CAS  Google Scholar  * Fei, H., Liu, Z., McCammon, C. & Katsura, T. Oxygen vacancy

substitution linked to ferric iron in bridgmanite at 27 GPa. _Geophys. Res. Lett._ 47, e2019GL086296 (2020). Article  CAS  Google Scholar  * Liu, Z. et al. Stability and solubility of the

FeAlO3 component in bridgmanite at uppermost lower mantle conditions. _J. Geophys. Res. Solid Earth_ 125, e2019JB018447 (2020). Article  CAS  Google Scholar  * Liu, Z. et al. Aluminum

solubility in bridgmanite up to 3000 K at the top lower mantle. _Geosci. Front._ 12, 929–935 (2021). Article  Google Scholar  * Wang, L., Liu, Z., Koizumi, S., Boffa Ballaran, T. &

Katsura, T. Aluminum components in bridgmanite coexisting with corundum and CF-phase with temperature. _J. Geophys. Res. Solid Earth_ 128, e2022JB025739 (2023). Article  CAS  Google Scholar

  * Liu, Z. et al. A new (Mg0.5Fe3+0.5)(Si0.5Al3+0.5)O3 LiNbO3-type phase synthesized at lower mantle conditions. _Am. Miner._ 104, 1223–1216 (2019). Article  Google Scholar  * Ishii, T.,

McCammon, C. & Katsura, T. Iron and aluminum substitution mechanism in the perovskite phase in the system MgSiO3-FeAlO3-MgO. _Am. Miner._ 108, 738–743 (2023). Article  Google Scholar  *

Wang, F. et al. A decrease in the Fe3+/∑Fe ratio of bridgmanite with temperature at the top of the lower mantle. _Earth Planet. Sci. Lett._ 624, 118440 (2023). Article  CAS  Google Scholar 

* Lauterbach, S., McCammon, C. A., van Aken, P., Langenhorst, F. & Seifert, F. Mossbauer and ELNES spectroscopy of (Mg,Fe)(Si,Al)O3 perovskite: a highly oxidised component of the lower

mantle. _Contrib. Mineral. Petrol._ 138, 17–26 (2000). Article  CAS  Google Scholar  * Frost, D. J. Fe2+-Mg partitioning between garnet, magnesiowustite, and (Mg,Fe)2SiO4 phases of the

transition zone. _Am. Miner._ 88, 387–397 (2003). Article  CAS  Google Scholar  * Grüninger, H. et al. Oxygen vacancy ordering in aluminous bridgmanite in the Earth’s lower mantle. _Geophys.

Res. Lett_. 46 https://doi.org/10.1029/2019GL083613 (2019). * Chanyshev, A. et al. Ferric Iron Substitution Mechanism in Bridgmanite under SiO2-Saturated Conditions at 27 GPa. _ACS Earth

Space Chem_ 7, 471–478 (2023). Article  CAS  Google Scholar  * Ishii, T. et al. High pressure-temperature phase relations of basaltic crust up to mid-mantle conditions. _Earth Planet. Sci.

Lett._ 584, 117472 (2022). Article  CAS  Google Scholar  * Liu, L. Post-oxide phases of forsterite and enstatite. _Geophys. Res. Lett._ 2, 417–419 (1975). Article  CAS  Google Scholar  *

Horiuchi, H., Ito, E. & Weidner, D. J. Perovskite-type MgSiO3 - single-crystal X-ray-diffraction study. _Am. Miner._ 72, 357–360 (1987). CAS  Google Scholar  * Tschauner, O. et al.

Discovery of davemaoite, CaSiO3-perovskite, as a mineral from the lower mantle. _Science_ 374, 891–894 (2021). Article  CAS  PubMed  Google Scholar  * Akaogi, M. High-pressure silicates and

oxides: phase transition and thermodynamics. Springer Singapore, 206. https://doi.org/10.1007/978-981-19-6363-6 (2022). * Shannon, R. D. Revised effective ionic radii and systematic studies

of interatomic distances in halides and chalcogenides. _Acta Crystallogr. A_ 32, 751–767 (1976). Article  Google Scholar  * Liu, Z. D. et al. Phase relations in the system MgSiO3-Al2O3 up to

52 GPa and 2000 K. _Phys. Earth Planet. Inter._ 257, 18–27 (2016). Article  CAS  Google Scholar  * Liu, Z. D., Ballaran, T. B., Huang, R., Frost, D. J. & Katsura, T. Strong correlation

of oxygen vacancies in bridgmanite with Mg/Si ratio. _Earth Planet. Sci. Lett._ 523, 10 (2019). Article  Google Scholar  * Sano-Furukawa, A., Kuribayashi, T., Komatsu, K., Yagi, T. &

Ohtani, E. Investigation of hydrogen sites of wadsleyite: a neutron diffraction study. _Phys. Earth Planet. Inter._ 189, 56–62 (2011). Article  CAS  Google Scholar  * Ross, N. L., Gibbs, G.

V. & Rosso, K. M. Potential docking sites and positions of hydrogen in high-pressure silicates. _Am. Miner._ 88, 1452–1459 (2003). Article  CAS  Google Scholar  * Townsend, J. P.,

Tsuchiya, J., Bina, C. R. & Jacobsen, S. D. First-principles investigation of hydrous postperovskite. _Phys. Earth Planet. Int._ 244, 42–48 (2015). Article  CAS  Google Scholar  *

Purevjav, N. et al. Hydrogen incorporation mechanism in the lower-mantle bridgmanite. _Am. Miner._ 109, 1036–1044 (2024). Article  Google Scholar  * Ito, E. & Takahashi, E. Postspinel

transformations in the system Mg2SiO4-Fe2SiO4 and some geophysical implications. _J. Geophys. Res. Solid Earth_ 94, 10637–10646 (1989). Article  Google Scholar  * Kato, T. et al. In situ X

ray observation of high-pressure phase transitions of MgSiO3 and thermal expansion of MgSiO3 perovskite at 25 GPa by double-stage multianvil system. _J. Geophys. Res. Solid Earth_ 100,

20475–20481 (1995). Article  Google Scholar  * Kuroda, K. et al. Determination of the phase boundary between ilmenite and perovskite in MgSiO3 by in situ X-ray diffraction and quench

experiments. _Phys. Chem. Miner._ 27, 523–532 (2000). Article  CAS  Google Scholar  * Ono, S. et al. In situ observation of ilmenite-perovskite phase transition in MgSiO3 using synchrotron

radiation. _Geophys. Res. Lett._ 28, 835–838 (2001). Article  CAS  Google Scholar  * Hirose, K., Komabayashi, T., Murakami, M. & Funakoshi, K. In situ measurements of the

majorite-akimotoite-perovskite phase transition boundaries in MgSiO3. _Geophys. Res. Lett._ 28, 4351–4354 (2001). Article  CAS  Google Scholar  * Ishii, T., Kojitani, H. & Akaogi, M.

Post-spinel transitions in pyrolite and Mg2SiO4 and akimotoite–perovskite transition in MgSiO3: Precise comparison by high-pressure high-temperature experiments with multi-sample cell

technique. _Earth Planet. Sci. Lett._ 309, 185–197 (2011). Article  CAS  Google Scholar  * Chanyshev, A. et al. Depressed 660-km discontinuity caused by akimotoite–bridgmanite transition.

_Nature_ 601, 69–73 (2022). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hernandez, J. A. et al. Direct observation of shock-induced disordering of enstatite below the melting

temperature. _Geophys. Res. Lett._ 47, e2020GL088887 (2020). Article  Google Scholar  * Yu, Y., Wentzcovitch, R. M., Vinograd, V. L. & Angel, R. J. Thermodynamic properties of MgSiO3

majorite and phase transitions near 660 Km depth in MgSiO3 and Mg2SiO4: a first principles study. _J. Geophys. Res. Solid Earth_ 116, B02208 (2011). Article  Google Scholar  * Ito, E. &

Yamada, H. Stability relations of silicate spinels, ilmenites, and perovskites. In: _Hig_h-pressure research in geophy_sics_, 405–419 (1982). * Ono, S. & Oganov, A. In situ observations

of phase transition between perovskite and CaIrO3-type phase in MgSiO3 and pyrolitic mantle composition. _Earth Planet. Sci. Lett._ 236, 914–932 (2005). Article  CAS  Google Scholar  *

Catalli, K., Shim, S. H. & Prakapenka, V. Thickness and Clapeyron slope of the postperovskite boundary. _Nature_ 462, 782–786 (2009). Article  CAS  PubMed  Google Scholar  * Tsuchiya,

T., Tsuchiya, J., Umemoto, K. & Wentzcovitch, R. A. Phase transition in MgSiO3 perovskite in the earth’s lower mantle. _Earth Planet. Sci. Lett._ 224, 241–248 (2004). Article  CAS 

Google Scholar  * Ito, E., Katsura, T. Melting of ferromagnesian silicates under the lower mantle conditions. _In_: Syono, Y., Manghnani, M. H. (Eds.), _High‐pressure research: application

to earth and planetary sciences_, 315–322. https://doi.org/10.1029/GM067p0315 (1992). * Zerr, A. & Boehler, R. Melting of (Mg, Fe)SiO3-perovskite to 625 Kilobars: indication of a high

melting temperature in the lower mantle. _Science_ 262, 553–555 (1993). Article  CAS  PubMed  Google Scholar  * Shen, G. Y. & Lazor, P. Measurement of melting temperatures of some

minerals under lower mantle pressures. _J. Geophys. Res. Solid Earth_ 100, 17699–17713 (1995). Article  CAS  Google Scholar  * Akins, J. A., Luo, S. N., Asimow, P. D. & Ahrens, T. J.

Shock-induced melting of MgSiO3 perovskite and implications for melts in Earth’s lowermost mantle -: art. no. L14612. _Geophys. Res. Lett._ 31, L14612 (2004). Article  Google Scholar  *

Mosenfelder, J. L., Asimow, P. D., Frost, D. J., Rubie, D. C. & Ahrens, T. J. The MgSiO3 system at high pressure: thermodynamic properties of perovskite, postperovskite, and melt from

global inversion of shock and static compression data. _J. Geophys. Res. Solid Earth_ 114, B01203 (2009). Article  Google Scholar  * de Koker, N. & Stixrude, L. Self-consistent

thermodynamic description of silicate liquids, with application to shock melting of MgO periclase and MgSiO3 perovskite. _Geophys. J. Int._ 178, 162–179 (2009). Article  Google Scholar  * Di

Paola, C. & Brodholt, J. P. Modeling the melting of multicomponent systems: the case of MgSiO3 perovskite under lower mantle conditions. _Sci Rep-Uk_ 6, 29830 (2016). Article  Google

Scholar  * Liebske, C. & Frost, D. J. Melting phase relations in the MgO–MgSiO3 system between 16 and 26GPa: implications for melting in Earth’s deep interior. _Earth Planet. Sci. Lett._

345-348, 159–170 (2012). Article  CAS  Google Scholar  * Pierru, R. et al. Solidus melting of pyrolite and bridgmanite: Implication for the thermochemical state of the Earth’s interior.

_Earth Planet. Sci. Lett._ 595, 117770 (2022). Article  CAS  Google Scholar  * Irifune, T. et al. The postspinel phase boundary in Mg2SiO4 determined by in situ x-ray diffraction. _Science_

279, 1698–1700 (1998). Article  CAS  PubMed  Google Scholar  * Fei, Y. et al. Experimentally determined postspinel transformation boundary in Mg2SiO4 using MgO as an internal pressure

standard and its geophysical implications. _J. Geophys. Res. Solid Earth_ 109, B02305 (2004). Article  Google Scholar  * Ghosh, S. et al. Effect of water in depleted mantle on post-spinel

transition and implication for 660 Km seismic discontinuity. _Earth Planet. Sci. Lett._ 371, 103–111 (2013). Article  Google Scholar  * Tsujino, N. et al. Phase transition of

wadsleyite-ringwoodite in the Mg2SiO4-Fe2SiO4 system. _Am. Miner._ 104, 588–594 (2019). Article  Google Scholar  * Yao, J., Frost, D. J. & Steinle-Neumann, G. Lower mantle melting:

experiments and thermodynamic modeling in the system MgO-SiO2. _J. Geophys. Res. Solid Earth_ 126, e2021JB022568 (2021). Article  CAS  Google Scholar  * Frost, D. J. & McCammon, C. A.

The redox state of Earth’s mantle. _Ann. Rev. Earth Planet. Sci._ 36, 389–420 (2008). Article  CAS  Google Scholar  * McCammon, C. Perovskite as a possible sink for ferric iron in the lower

mantle. _Nature_ 387, 694–696 (1997). Article  CAS  Google Scholar  * Liu, L. G. Orthorhombic perovskite phases observed in olivine, pyroxene and garnet at high pressures and temperatures.

_Phys. Earth Planet. Inter._ 11, 289–298 (1976). Article  CAS  Google Scholar  * Kudoh, Y., Prewitt, C. T., Finger, L. W., Darovskikh, A. & Ito, E. Effect of Iron on the

crystal-structure of (Mg,Fe)SiO3 perovskite. _Geophys. Res. Lett._ 17, 1481–1484 (1990). Article  CAS  Google Scholar  * Ito, E., Takahashi, E. & Matsui, Y. The mineralogy and chemistry

of the lower mantle: an implication of the ultrahigh-pressure phase relations in the system MgO-FeO-SiO2. _Earth Planet. Sci. Lett._ 67, 238–248 (1984). Article  CAS  Google Scholar  * Fei,

Y. W., Wang, Y. B. & Finger, L. W. Maximum solubility of FeO in (Mg, Fe)SiO3-perovskite as a function of temperature at 26 GPa: Implication for FeO content in the lower mantle. _J.

Geophys. Res. Solid Earth_ 101, 11525–11530 (1996). Article  Google Scholar  * Tange, Y., Takahashi, E., Nishihara, Y., Funakoshi, K.I. & Sata, N. Phase relations in the system

MgO-FeO-SiO2 to 50 GPa and 2000 degrees C: an application of experimental techniques using multianvil apparatus with sintered diamond anvils. _J. Geophys. Res. Solid Earth_ 114, B02214

(2009). Article  Google Scholar  * Arimoto, T. et al. Phase relations of MgSiO3-FeSiO3 system up to 64 GPa and 2300 K using multianvil apparatus with sintered diamond anvils. _Phys. Earth

Planet. Inter._ 295, 106297 (2019). Article  CAS  Google Scholar  * Mao, H.-K., Shen, G. & Hemley, R. J. Multivariable dependence of Fe-Mg partitioning in the lower mantle. _Science_

278, 2098–2100 (1997). Article  CAS  PubMed  Google Scholar  * Lin, J.-F., Speziale, S., Mao, Z. & Marquardt, H. Effects of the electronic spin transitions of iron in lower mantle

minerals: implications for deep mantle geophysics and geochemistry. _Rev. Geophys._ 51, 244–275 (2013). Article  Google Scholar  * Yoshino, T., Kamada, S., Zhao, C., Ohtani, E. & Hirao,

N. Electrical conductivity model of Al-bearing bridgmanite with implications for the electrical structure of the Earth’s lower mantle. _Earth Planet. Sci. Lett._ 434, 208–219 (2016). Article

  CAS  Google Scholar  * Huang, R. et al. The composition and redox state of bridgmanite in the lower mantle as a function of oxygen fugacity. _Geochim. Cosmochim. Acta_ 303, 110–136 (2021).

Article  CAS  Google Scholar  * Katsura, T. & Ito, E. Determination of Fe-Mg partitioning between perovskite and magnesiowustite. _Geophys. Res. Lett._ 23, 2005–2008 (1996). Article 

CAS  Google Scholar  * Martinez, I., Wang, Y. B., Guyot, F., Liebermann, R. C. & Doukhan, J. C. Microstructures and iron partitioning in (Mg,Fe)SiO3 perovskite (Mg,Fe)O magnesiowustite

assemblages: an analytical transmission electron microscopy study. _J. Geophys. Res. Solid Earth_ 102, 5265–5280 (1997). Article  CAS  Google Scholar  * Frost, D. J. & Langenhorst, F.

The effect of Al2O3 on Fe-Mg partitioning between magnesiowustite and magnesium silicate perovskite. _Earth Planet. Sci. Lett._ 199, 227–241 (2002). Article  CAS  Google Scholar  * Nakajima,

Y., Frost, D. J. & Rubie, D. C. Ferrous iron partitioning between magnesium silicate perovskite and ferropericlase and the composition of perovskite in the Earth’s lower mantle. _J.

Geophys. Res. Solid Earth_ 117, 12 (2012). Article  Google Scholar  * Andrault, D. Evaluation of (Mg,Fe) partitioning between silicate perovskite and magnesiowustite up to 120 GPa and 2300K.

_J. Geophys. Solid Earth_ 106, 2079–2087 (2001). Article  CAS  Google Scholar  * Kesson, S. E., Fitz Gerald, J. D., O’Neill, H. S. & Shelley, J. M. G. Partitioning of iron between

magnesian silicate perovskite and magnesiowiistite at about 1 Mbar. _Phys. Earth Planet. Inter._ 131, 295–310 (2002). Article  CAS  Google Scholar  * Auzende, A. L. et al. Element

partitioning between magnesium silicate perovskite and ferropericlase: new insights into bulk lower-mantle geochemistry. _Earth Planet. Sci. Lett._ 269, 164–174 (2008). Article  CAS  Google

Scholar  * Sinmyo, R. et al. Partitioning of iron between perovskite/postperovskite and ferropericlase in the lower mantle. _J. Geophys. Res. Solid Earth_ 113, B11204 (2008). Article  Google

Scholar  * Nomura, R., Zhou, Y. & Irifune, T. Melting phase relations in the MgSiO3–CaSiO3 system at 24 GPa. _Prog. Earth Planet. Sci._ 4, 34 (2017). Article  Google Scholar  * Corgne,

A., Liebske, C., Wood, B. J., Rubie, D. C. & Frost, D. J. Silicate perovskite-melt partitioning of trace elements and geochemical signature of a deep perovskitic reservoir. _Geochim.

Cosmochim. Acta_ 69, 485–496 (2005). Article  CAS  Google Scholar  * Irifune, T., Susaki, J., Yagi, T. & Sawamoto, H. Phase-transformations in diopside CaMgSi2O6 at pressures up to 25

GPa. _Geophys. Res. Lett._ 16, 187–190 (1989). Article  CAS  Google Scholar  * Irifune, T., Susaki, J., Yagi, T. & Sawamoto, H. High-pressure phase transformation in CaMgSi2O6 and

implications for origin of ultra-deep diamond inclusions. _Geophys. Res. Lett_. 27, 3541–3544 (2000). * Creasy, N., Girard, J., Eckert, J. O. & Lee, K. K. M. The Role of redox on

bridgmanite crystal chemistry and calcium speciation in the lower mantle. _J. Geophys. Res. Solid Earth_ 125, e2020JB020783 (2020). Article  CAS  Google Scholar  * Liu, L. G. Silicate

perovskite from phase transformations of pyrope-garnet at high pressure and temperature. _Geophys. Res. Lett._ 1, 277–280 (1974). Article  CAS  Google Scholar  * Liu, L. G. High-pressure

reconnaissance investigation in the system Mg3Al2Si3O12-Fe3Al2Si3O12. _Earth Planet. Sci. Lett._ 26, 425–433 (1975). Article  CAS  Google Scholar  * Liu, L.-G. The system enstatite-pyrope at

high pressures and temperatures and the mineralogy of the Earth’s mantle. _Earth Planet. Sci. Lett._ 36, 237–245 (1977). Article  CAS  Google Scholar  * Irifune, T., Koizumi, T. & Ando,

J. I. An experimental study of the garnet-perovskite transformation in the system MgSiO3-Mg3Al2Si3O12. _Phys. Earth Planet. Inter._ 96, 147–157 (1996). Article  CAS  Google Scholar  *

Akaogi, M. & Ito, E. Calorimetric study on majorite-perovskite transition in the system Mg4Si4O12-Mg3Al2Si3O12: transition boundaries with positive pressure-temperature slopes. _Phys.

Earth Planet. Inter._ 114, 129–140 (1999). Article  CAS  Google Scholar  * Kubo, A. & Akaogi, M. Post-garnet transitions in the system Mg4Si4O12-Mg3Al2Si3O12 up to 28 GPa: phase

relations of garnet, ilmenite and perovskite. _Phys. Earth Planet. Inter._ 121, 85–102 (2000). Article  CAS  Google Scholar  * Hirose, K., Fei, Y. W., Ono, S., Yagi, T. & Funakoshi, K.

In situ measurements of the phase transition boundary in Mg3Al2Si3O12: implications for the nature of the seismic discontinuities in the Earth’s mantle. _Earth Planet. Sci. Lett._ 184,

567–573 (2001). Article  CAS  Google Scholar  * Akaogi, M., Tanaka, A. & Ito, E. Garnet-ilmenite-perovskite transitions in the system Mg4Si4O12-Mg3Al2Si3O12 at high pressures and high

temperatures: phase equilibria, calorimetry and implications for mantle structure. _Phys. Earth Planet. Inter._ 132, 303–324 (2002). Article  CAS  Google Scholar  * Navrotsky, A. et al.

Aluminum in magnesium silicate perovskite: formation, structure, and energetics of magnesium-rich defect solid solutions. _J. Geophys. Res. Solid Earth_ 108, 2330 (2003). Article  Google

Scholar  * Yamamoto, T., Yuen, D. A. & Ebisuzaki, T. Substitution mechanism of Al ions in MgSiO3 perovskite under high pressure conditions from first-principles calculations. _Earth

Planet. Sci. Lett._ 206, 617–625 (2003). Article  CAS  Google Scholar  * Akber-Knutson, S. & Bukowinski, M. S. T. The energetics of aluminum solubility into MgSiO3 perovskite at lower

mantle conditions. _Earth Planet. Sci. Lett._ 220, 317–330 (2004). Article  CAS  Google Scholar  * Panero, W. R., Akber-Knutson, S. & Stixrude, L. Al2O3 incorporation in MgSiO3

perovskite and ilmenite. _Earth Planet. Sci. Lett._ 252, 152–161 (2006). Article  CAS  Google Scholar  * Walter, M. J. et al. Subsolidus phase relations and perovskite compressibility in the

system MgO-AlO1.5-SiO2 with implications for Earth’s lower mantle. _Earth Planet. Sci. Lett._ 248, 77–89 (2006). Article  CAS  Google Scholar  * Tsuchiya, J. & Tsuchiya, T.

Postperovskite phase equilibria in the MgSiO3-Al2O3 system. _Proc. Natl. Acad. Sci. USA._ 105, 19160–19164 (2008). Article  CAS  PubMed  PubMed Central  Google Scholar  * Ishii, T. et al.

Synthesis and crystal structure of LiNbO3-type Mg3Al2Si3O12: a possible indicator of shock conditions of meteorites. _Am. Miner._ 102, 1947–1952 (2017). Article  Google Scholar  * Liu,

Z.-D., Ishii, T. & Katsura, T. Rapid decrease in oxygen-vacancy substitution in aluminous bridgmanite with pressure. _Geochem. Persp. Lett._ 5, 12–18 (2017). Article  Google Scholar  *

Irifune, T., Fujino, K. & Ohtani, E. A new high-pressure form of MgAl2O4. _Nature_ 349, 409–411 (1991). Article  CAS  Google Scholar  * Ishii, T. et al. High-pressure phase relations and

crystal structures of postspinel phases in MgV2O4, FeV2O4, and MnCr2O4: Crystal chemistry of AB2O4 postspinel compounds. _Inorg. Chem._ 57, 6648–6657 (2018c). Article  CAS  PubMed  Google

Scholar  * Kojitani, H., Hisatomi, R. & Akaogi, M. High-pressure phase relations and crystal chemistry of calcium ferrite-type solid solutions in the system MgAl2O4-Mg2SiO4. _Am. Miner._

92, 1112–1118 (2007). Article  CAS  Google Scholar  * Liu, Z. et al. Phase relations in the system MgSiO3–Al2O3 up to 2300 K at lower-mantle pressures. _J. Geophys. Res. Solid Earth_ 122,

7775–7788 (2017). Article  CAS  Google Scholar  * Muir, J. M. R., Thomson, A. R. & Zhang, F. W. The miscibility of calcium silicate perovskite and bridgmanite: a single perovskite solid

solution in hot, iron-rich regions. _Earth Planet. Sci. Lett._ 566, 10 (2021). Article  Google Scholar  * Funamori, N. & Jeanloz, R. High-pressure transformation of Al2O3. _Science_ 278,

1109–1111 (1997). Article  CAS  Google Scholar  * Hirsch, L. M. & Shankland, T. J. Point-defects in (Mg,Fe)SiO3 perovskite. _Geophys. Res. Lett._ 18, 1305–1308 (1991). Article  CAS 

Google Scholar  * Kojitani, H., Katsura, T. & Akaogi, M. Aluminum substitution mechanisms in perovskite-type MgSiO3: an investigation by Rietveld analysis. _Phys. Chem. Miner._ 34,

257–267 (2007). Article  CAS  Google Scholar  * Liu, Z., Akaogi, M. & Katsura, T. Increase of the oxygen vacancy component in bridgmanite with temperature. _Earth Planet. Sci. Lett._

505, 141–151 (2019). Article  CAS  Google Scholar  * Stebbins, J. F., Kojitani, H., Akaogi, M. & Navrotsky, A. Aluminum substitution in MgSiO3 perovskite: investigation of multiple

mechanisms by Al-27 NMR. _Am. Miner._ 88, 1161–1164 (2003). Article  CAS  Google Scholar  * Stebbins, J. F. et al. Aluminum substitution in stishovite and MgSiO3 perovskite: high-resolution

Al-27 NMR. _Am. Miner._ 91, 337–343 (2006). Article  CAS  Google Scholar  * Hummer, D. R. & Fei, Y. Synthesis and crystal chemistry of Fe3+-bearing (Mg,Fe3+)(Si,Fe3+)O3 perovskite. _Am.

Miner._ 97, 1915–1921 (2012). Article  CAS  Google Scholar  * Fei, H. et al. Pressure destabilizes oxygen vacancies in bridgmanite. _J. Geophys. Res. Solid Earth_ 126, e2021JB022437 (2021).

Article  CAS  Google Scholar  * Bykova, E. et al. Structural complexity of simple Fe2O3 at high pressures and temperatures. _Nat. Commun._ 7, 10661 (2016). Article  CAS  PubMed  PubMed

Central  Google Scholar  * Huang, R. et al. The Effect of Fe‐Al substitution on the crystal Structure of MgSiO3 bridgmanite. _J. Geophys. Res. Solid Earth_ 126, e2021JB021936 (2021). Article

  CAS  Google Scholar  * Nishio-Hamane, D., Nagai, T., Fujino, K., Seto, Y. & Takafuji, N. Fe3+ and Al solubilities in MgSiO3 perovskite: implication of the Fe3+AlO3 substitution in

MgSiO3 perovskite at the lower mantle condition. _Geophys. Res. Lett._ 32, L16306 (2005). Article  Google Scholar  * Boffa Ballaran, T. et al. Effect of chemistry on the compressibility of

silicate perovskite in the lower mantle. _Earth Planet. Sci. Lett._ 333–334, 181–190 (2012). Article  Google Scholar  * Sinmyo, R., Hirose, K., Muto, S., Ohishi, Y. & Yasuhara, A. The

valence state and partitioning of iron in the Earth’s lowermost mantle. _J. Geophys. Res._ 116, B07205 (2011). Google Scholar  * Prescher, C., Langenhorst, F., Dubrovinsky, L. S.,

Prakapenka, V. B. & Miyajima, N. The effect of Fe spin crossovers on its partitioning behavior and oxidation state in a pyrolitic Earth’s lower mantle system. _Earth Planet. Sci Lett._

399, 86–91 (2014). Article  CAS  Google Scholar  * Piet, H. et al. Spin and valence dependence of iron partitioning in Earth’s deep mantle. _Proc. Natl. Acad. Sci. USA._ 113, 11127–11130

(2016). Article  CAS  PubMed  PubMed Central  Google Scholar  * Irifune, T. et al. Iron partitioning and density changes of pyrolite in Earth’s lower mantle. _Science_ 327, 193–195 (2010).

Article  CAS  PubMed  Google Scholar  * Stixrude, L. & Lithgow-Bertelloni, C. Thermal expansivity, heat capacity and bulk modulus of the mantle. _Geophys. J. Int._ 228, 1119–1149 (2022).

Article  CAS  Google Scholar  * Stixrude, L. & Lithgow-Bertelloni, C. Thermodynamics of mantle minerals - II. Phase equilibria. _Geophys. J. Int._ 184, 1180–1213 (2011). Article  CAS 

Google Scholar  * Katsura, T. & Tange, Y. A simple derivation of the Birch–Murnaghan equations of state (EOSs) and comparison with EOSs derived from other definitions of finite strain.

_Miner_ 9, 745 (2019). CAS  Google Scholar  * Poierier, J. P. Introduction to the Physics of the Earth’s Interior, 2nd edition. Cambridge University Press, Cambridge, 328.

https://doi.org/10.1017/CBO9781139164467 (2012). * Frost, D. J. et al. Experimental evidence for the existence of iron-rich metal in the Earth’s lower mantle. _Nature_ 428, 409–412 (2004).

Article  CAS  PubMed  Google Scholar  * Frost, D.J. & McCammon, C.A. The redox state of Earth’s mantle. _Annu. Rev. Earth Planet. Sci._ 36, 389–420 (2008). * Meade, C., Reffner, J. A.

& Ito, E. Synchrotron infrared absorbance measurements of hydrogen in MgSiO3 perovskite. _Science_ 264, 1558–1560 (1994). Article  CAS  PubMed  Google Scholar  * Murakami, M. et al.

Water in Earth’s lower mantle. _Science_ 295, 1885–1887 (2002). Article  CAS  PubMed  Google Scholar  * Bolfan-Casanova, N., Keppler, H. & Rubie, D. C. Water partitioning at 660 Km depth

and evidence for very low water solubility in magnesium silicate perovskite. _Geophys. Res. Lett._ 30, 1905 (2003). Article  Google Scholar  * Litasov, K. et al. Water solubility in

Mg-perovskites and water storage capacity in the lower mantle. _Earth Planet. Sci. Lett._ 211, 189–203 (2003). Article  CAS  Google Scholar  * Inoue, T., Wada, T., Sasaki, R. & Yurimoto,

H. Water partitioning in the Earth’s mantle. _Phys. Earth Planet. Int._ 183, 245–251 (2010). Article  CAS  Google Scholar  * Panero, W. R. et al. Dry (Mg,Fe)SiO3 perovskite in the Earth’s

lower mantle. _J. Geophys. Res. Solid Earth_ 120, 894–908 (2015). Article  CAS  Google Scholar  * Fu, S. et al. Water concentration in single-crystal (Al,Fe)-bearing bridgmanite grown from

the hydrous melt: implications for dehydration melting at the topmost lower mantle. _Geophys. Res. Lett._ 46, 10346–10357 (2019). Article  CAS  Google Scholar  * Liu, Z. et al. Bridgmanite

is nearly dry at the top of the lower mantle. _Earth Planet. Sci. Lett._ 570, 117088 (2021). Article  CAS  Google Scholar  * Ishii, T., Ohtani, E. & Shatskiy, A. Aluminum and hydrogen

partitioning between bridgmanite and high-pressure hydrous phases: implications for water storage in the lower mantle. _Earth Planet. Sci. Lett._ 583, 117441 (2022). Article  CAS  Google

Scholar  * Yang, Y. N. et al. NanoSIMS analysis of water content in bridgmanite at the micron scale: an experimental approach to probe water in Earth’s deep mantle. _Front. Chem._ 11,

1166593 (2023). Article  CAS  PubMed  PubMed Central  Google Scholar  * Hernández, E. R., Alfè, D. & Brodholt, J. The incorporation of water into lower-mantle perovskites: a

first-principles study. _Earth Planet. Sci. Lett._ 364, 37–43 (2013). Article  Google Scholar  * Ito, E. & Weidner, D. J. Crystal growth of MgSiO3 perovskite. _Geophys. Res. Lett._ 13,

464–466 (1986). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS I thank Msasaki Akaogi for producing Fig. 2 and Fei Wang for calculating the Bdm compositions shown in Fig.

 S1. I acknowledge Christian Liebske and three anonymous reviewers for their helpful comments. This work was funded by a research project approved by the European Research Council (ERC)

under the European Union’s Horizon 2020 research and innovation program (Proposal no. 787527) AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Bayerisches Geoinstitut, University of Bayreuth,

Bayreuth, Germany Tomoo Katsura Authors * Tomoo Katsura View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS T.K. conducted all scientific work

except for preparing Figs. 2 and S1. CORRESPONDING AUTHOR Correspondence to Tomoo Katsura. ETHICS DECLARATIONS COMPETING INTERESTS The author declares competing interests. PEER REVIEW PEER

REVIEW INFORMATION _Communications Chemistry_ thanks Christian Liebske and the other, anonymous, reviewers for their contribution to the peer review of this work. ADDITIONAL INFORMATION

PUBLISHER’S NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY MATERIAL

RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use,

sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons

licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or

other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in

the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the

copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Katsura, T. Phase

relations of bridgmanite, the most abundant mineral in the Earth’s lower mantle. _Commun Chem_ 8, 28 (2025). https://doi.org/10.1038/s42004-024-01389-8 Download citation * Received: 20 May

2024 * Accepted: 06 December 2024 * Published: 01 February 2025 * DOI: https://doi.org/10.1038/s42004-024-01389-8 SHARE THIS ARTICLE Anyone you share the following link with will be able to

read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing

initiative