Reader TTS

ABSTRACT Spin Hall effect of light is a spin-dependent transverse shift of optical beam propagating along a curved trajectory, where the refractive index gradient plays a role of the

electric field in spin Hall effect of solid-state systems. In order to observe optical spin Hall shift in a refraction taking place at air-glass interface, an amplification technique was

necessary such as quantum weak measurement. In phase-discontinuity metasurface (PMS) a rapid phase-change along metasurface takes place over subwavelength distance, which leads to a large

refractive index gradient for refraction beam enabling a direct detection of optical spin Hall shift without amplification. Here, we identify that the relative optical spin Hall shift

depends on incidence angle at PMS and demonstrate a control of optical spin Hall shift by constructing weak value measurement with a variable phase retardance in the post-selection.

Capability of optical spin Hall shift control permits a tunable precision metrology applicable to nanoscale photonics such as angular momentum transfer and sensing. SIMILAR CONTENT BEING

VIEWED BY OTHERS DISPERSION-ENGINEERED SPIN PHOTONICS BASED ON FOLDED-PATH METASURFACES Article Open access 16 May 2025 EXCITATION OF OPTICAL TAMM STATE FOR PHOTONIC SPIN HALL ENHANCEMENT

Article Open access 02 January 2024 REACHING THE HIGHEST EFFICIENCY OF SPIN HALL EFFECT OF LIGHT IN THE NEAR-INFRARED USING ALL-DIELECTRIC METASURFACES Article Open access 19 April 2022

INTRODUCTION According to Maxwell’s description, the transversality is a fundamental property of electromagnetic wave. In an optical beam propagating along a curved trajectory, the

transversality results in spin-orbit interaction, which is one example of interaction Hamiltonians coupling slow and fast systems. A coupling of slow and fast systems leads to reciprocal

effects of action and reaction between the two systems, which are described coherently in terms of the Berry phase and curvature1,2. In addition, the presence of a degenerate point in the

energy-momentum dispersion relation of light allows an introduction of topological magnetic monopole in describing spin-orbit interaction3,4. In spin-orbit interaction of an optical beam

along a curved trajectory, the beam trajectory and optical spin correspond to the slow and fast systems, respectively. Polarization-plane rotation of light along a coiled optical fiber

results from the effect of a curved beam trajectory (slow) on optical spin (fast), which is a manifestation of the Berry phase in the light polarization5. On the other hand, the effect of

optical spin (fast) on a curved beam trajectory (slow) gives rise to a spin-dependent transverse shift of optical beam centroid, i.e., spin Hall effect of light (SHEL)6,7. The beam

trajectory is described by the Lorentz force in momentum space, , where is the refractive index gradient and is the topological magnetic monopole Berry curvature associated with optical beam

of spin λ8,9,10. In air-glass interface, the magnitude of is not large enough and in order to obtain an image showing optical spin Hall transverse shift, it was necessary to adopt a

multiplying prism to have multiple total internal reflections7. In the case of refraction at air-glass interface, a direct detection of the spin-dependent transverse shift was not readily

feasible and a weak measurement amplification technique was adopted for observation, where a nearly crossed polarizer/analyzer is employed to amplify optical spin Hall shift by means of a

quantum weak measurement11,12. Direct observation of optical spin Hall shift in far-field has been realized in artificial optical structures such as an array of plasmonic rectangular

apertures and dielectric gradient metasurfaces13,14. In contrast, in a phase-discontinuity metasurface (PMS) composed of an array of V-shaped antennas, a rapid phase-change along metasurface

over subwavelength distance leads to a large refractive index gradient for cross-polarized scattering lights15. The magnitude of SHEL transverse shift is in the order of a few hundreds

nanometers at the near IR spectral range, which was directly detected without resorting to a weak measurement amplification technique16. One distinct feature of PMS is that the refractive

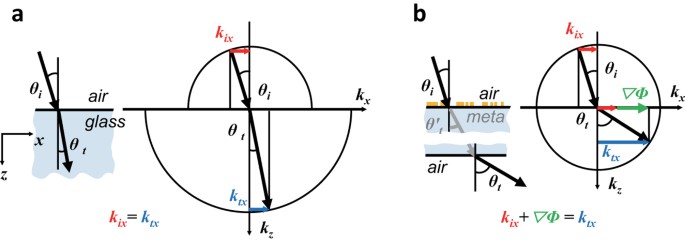
index gradient is tangential to the metasurface, differently from air-glass interface where the refractive index gradient is normal to the interface. At air-glass interface shown in Fig.

1(a), the radii of circular equifrequency contour are different in air and glass and transverse shifts cancel out at top and bottom parallel interfaces possessing opposite refractive index

gradients11. At PMS on a glass substrate, in contrast, the net transverse shift comes from the refractive index gradient of metasurface as shown in Fig. 1(b) with a single circular

equifrequency contour with the radius specified by the energy-momentum of light in air. In this article, first we derive an expression of optical spin Hall transverse shift in PMS. Since the

refractive index gradient is tangential to metasurface, rotational symmetry with respect to the surface normal is broken and conservation of total angular momentum does not hold for an

optical beam passing through PMS. However, an analysis based on the Berry connection allows for an analytic expression of optical spin Hall transverse shift. Next we show both theoretically

and experimentally that the sign of relative transverse shift depends on incidence angle which is understood in terms of an analytic expression of optical spin Hall transverse shift as well

as the Berry curvature. Then, we introduce a weak value measurement to control the sign and magnitude of transverse shift by manipulating optical phase retardance in the post-selection.

Finally, we demonstrate dynamic control of transverse shift by varying an electric voltage applied to the liquid crystal variable retarder. RESULTS OPTICAL SPIN HALL SHIFT IN PMS In the

equifrequency surface of PMS shown in Fig. 2 the refractive index gradient is along _x_-axis and the topological magnetic monopole Berry curvatures are radial vectors with directions

determined by incidence and refraction angles θ_i_ and θ_t_. Transverse shift _δy_ upon refraction at PMS is related to the phase gradient and the Berry connections of incidence and

refraction beams, yielding an expression of transverse shift:9,17 See Supplementary Eq. S2 for derivation of Eq. (1). From the two facts that both positive and negative refractions can take

place at PMS and that is tangential to PMS surface, the sign and magnitude of transverse shift _δy_ depend on incidence and refraction angles θ_i_ and θ_t_ as well as , as can be read-off

from Fig. 2 and Eq. (1). Figure 3(a) shows examples how the relative transverse shift of optical beams with spins ±1 changes sign in detail. For λ = +1 corresponding to the red arrows in

Fig. 3(a), when θ_i_ < θ_t_ a positive transverse shift (_δy_ > 0) takes place in both positive (①) and negative (②) refractions and when θ_i_ > θ_t_ a negative transverse shift

(_δy_ < 0) takes place in both negative (③) and positive (④) refractions. In Fig. 3(b) are plotted theoretical calculation (solid curves) and experimental measurement (solid circles) of

refraction angle θ_t_ and transverse shift _δy_ as a function of incidence angle θ_i_. WEAK VALUE OF OPTICAL SPIN HALL SHIFT POST-SELECTED WITH A PHASE RETARDANCE Weak measurement

amplification technique enabled an observation of optical spin Hall shift in air-glass interface11. By preparing a polarizer as pre-selection, the weak value is measured by a strong

measurement with a nearly cross-polarized analyzer as the post-selection18. In PMS, on the other hand, it is not necessary to adopt weak measurement amplification technique for an

observation of optical spin Hall shift. However, when it is attempted to control the transverse shift in PMS by an optical means, a weak value measurement can be utilized with a variable

phase retardance in the post-selection. Optical spin Hall shift is one example of classical analogues of a quantum measurement of the polarization state of a paraxial beam by its transverse

amplitude distribution19. By introducing a variable optical phase retardance in the post-selection, we can tune the post-selection state across the whole range of retardance, [0, π/2], to

control optical spin Hall shift, which is made possible in PMS since optical spin Hall shift is large enough to be detected in the optical far field. We place a phase retarder with variable

retardance Γ (modulus of π) inside a cross polarizer/analyzer (_P_1/_P_2) setup in order to control optical spin Hall shift in the weak measurement as shown in Fig. 4(a), where the

post-selection state is . When optical spin Hall transverse shift is measured at the propagation distance _z_ of a Gaussian beam with Rayleigh range of _z_0, the observable _metaSHEL_ is

expressed in terms of the Pauli matrix in the linear polarization bases:17,20,21 The weak value of transverse shift, post-selected at a retardance Γ, is readily obtained. Note that the phase

retardance (0 < ε ≪ 1) is the range where a weak measurement amplification is achieved. In Fig. 4(b) is plotted the transmitted light intensity through the cross polarizer/analyzer setup

of Fig. 4(a) as a function of retardance Γ. Figure 4(c) shows the weak value, _δy__w_(Γ), of an optical beam normally incident on PMS as a function of retardance Γ along with the

corresponding transverse shift _δy_. At Γ = 1/4 the weak value _δy__w_(Γ = 1/4) = 7.44_μm_, which corresponds to the transverse shift _δy_ = 124 _nm_ in the absence of a cross-polarized

polarizer/analyzer setup. It is important to note that the phase-retardance dependent weak value is measured in the optical far field22,23,24. IMAGES OF SPIN-DEPENDENT OPTICAL SPIN HALL

SHIFTS In order to obtain images of spin-dependent optical spin Hall shifts we employed InGaAs-based NIR camera. After two separate measurements of and , we calculated from each pixel

signals. We examined how optical spin Hall shift behaves for _s_-polarization (_y_-polarization) and _p_-polarization (_x_-polarization) of extraordinary refraction beam. In Fig. 5(a) blue

and red solid circles correspond to _s_-polarization (_y_-polarization) and _p_-polarization (_x_-polarization), respectively. As shown in Fig. 5(b,c), the relative transverse shifts show a

sign reversal with the same magnitude, which is different from those observed in air-glass interface. CONTROL OF OPTICAL SPIN HALL TRANSVERSE SHIFT BY WEAK MEASUREMENT POST-SELECTION Since

the weak value is post-selected at phase retardance Γ, an electric manipulation of phase retardance in LCVR allows a control of the weak value _δy__w_. A saw-tooth waveform of LCVR driving

voltage is programmed as shown in Fig. 6(a) to obtain a time-varying phase retardation and Fig. 6(b) is a plot of the measured phase retardance of LCVR as a function of LCVR driving voltage.

On the top panel of Fig. 6(c) is re-plotted the transmitted light intensity in Fig. 4(b) as a function of LCVR driving voltage, corresponding to the value of SUM = _q_1 + _q_2 + _q_3 + _q_4

of a position-sensitive detector (PSD). On the bottom panel of Fig. 6(c) is plotted the product of the transmitted light intensity in Fig. 4(b) and the relative transverse shift in Fig.

4(c) as a function of LCVR driving voltage, corresponding to the value of Y = (_q_1 + _q_2) − (_q_3 + _q_4) of the PSD, associated with optical spin Hall shift. Here, _q_1, _q_2, _q_3 and

_q_4 represent upper left, upper right, lower left and lower right quadrant of the PSD. In order to demonstrate a dynamic control of transverse shift, we monitored SUM and Y from the PSD by

oscilloscope, where a saw-tooth waveform of LCVR driving voltage is adopted with 1.0 _V_ and 3.0 _V_ as the initial and final voltages, covering the phase retardance from 0 to 1 (modulus of

π). Dual oscilloscope traces of a saw-tooth waveform of LCVR driving voltage (channel 2) and SUM (channel 1) are shown in Fig. 6(d) and dual oscilloscope traces of SUM (channel 1) and Y

(channel 2) are shown in Fig. 6(e). As can be seen in Fig. 6(e), there occurs a sign reversal in Y (channel 2) at LCVR driving voltage of 1.45 _V_ corresponding to , in the vicinity of which

a weak measurement amplification is achieved. This leads to a switching behavior of post-selected optical spin Hall transverse shift when the phase retardance is varied crossing .

Furthermore, the sign and magnitude of optical spin Hall shift is precisely controllable by manipulating phase retardation at a given incidence angle. This has an important application to

scanning chiral surface to identify spatial distribution of handedness of chirality in high resolution, for example, at biomaterial surface or chiral-dependent reflective surface25. In Fig.

6(f) is demonstrated a switching between positive and negative Y (channel 2) as the driving voltage (channel 1) is alternated between 1.25 _V_ (Γ = 0.65) and 1.77 _V_ (Γ = 0.35). Switching

operation of post-selected optical spin Hall shift has a potential application to signal processing in nanoscale photonics. In conclusion, the Berry connection and curvature are introduced

to describe optical spin Hall shift in phase-discontinuity metasurface. A large refractive index gradient tangential to metasurface allows a sign change in relative transverse shift, upon

varying incidence angle of an optical beam. By adopting a weak value measurement, it is demonstrated that optical spin Hall shift can be controlled by manipulating optical phase retardance

in the post-selection. Furthermore, switching operation of post-selected optical spin Hall shift is shown as an example of dynamic control of transverse shift. Control of optical spin Hall

shift in the optical far field has strong implication of applications where optical spin is utilized as a degree of freedom for signal processing, angular momentum transfer, sensing and

scanning chiral surface. METHODS SAMPLE FABRICATION Phase-discontinuity metasurface is composed of V-shape antenna pattern15. A linear array of eight V-shape apertures is repeated along

_x_-axis with the lattice constant Γ of 2400 nm. Focused ion beam milling is utilized to fabricate Babinet complementary V-shaped antennas on e-beam evaporated 30 nm-thick Au film on top of

fused silica substrate with adhesion layer of 3 nm thick titanium26. EXPERIMENTAL SET-UP We adopted 10 _mW λ_ = 1310 _nm_ pigtail style self-contained thermally stabilized laser diode as the

light source (OZ optics-OZ-2000) with the output fiber diameter 50 μm. The beam passes through a Glan/Thomson polarizer _P_1 (Thorlabs-GL10-C) to be linearly polarized. Then it is focused

onto the metasurface with a microscope objective lens, _f_ = 95 _mm_, to a 1/_e_2 intensity spot size _w_0 = 50_μm_. The extraordinary refraction beam is collected with a microscope

objective lens, _f_ = 95 _mm_ and a liquid crystal variable retarder (Thorlabs-LCC1113-C) and a second polarizer _P_2 are adopted to resolve the polarization state with an InGaAs-based NIR

camera (Ophir-XC-130) and InGaAs-based quadrant position sensitive detector (Newport-2903) with a 3-mm diameter active region is employed for imaging and detection. In our experimental

set-up, the propagation distance is _z_ = _f_ = 60 _z_0. Position sensitive detector is connected to the oscilloscope and the position X, Y and SUM data are monitored. The relative

transverse shift , which is obtained from the light intensity measurement by a photo-reciver placed on two-dimensional translation stage. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE:

Lee, Y.U. and Wu, J.W. Control of optical spin Hall shift in phase-discontinuity metasurface by weak value measurement post-selection. _Sci. Rep._ 5, 13900; doi: 10.1038/srep13900 (2015).

REFERENCES * Berry, M. V. The Quantum Phase, Five Years After in Geometric Phases in Physics (eds Wilczek, F. & Shapere, A. ) 7–28 (World Scientific, 1989). * Liberman, V. S. &

Zeldovich, B. Y. Spin-orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 46, 5199 (1992). Article  CAS  ADS  Google Scholar  * Berry, M. V. Quantal phase factors

accompanying adiabatic changes. Proc. R. Soc. Lond. A 392, 45–57 (1984). Article  ADS  MathSciNet  Google Scholar  * Bliokh, K. Y., Niv, A., Kleiner, V. & Hasman, E. Geometrodynamics of

spinning light. Nat. Phot. 2, 748–753 (2008). Article  CAS  Google Scholar  * Chiao, R. Y. & Wu, Y.-S. Manifestations of Berry’s topological phase for the photon. Phys. Rev. Lett. 57,

933–936 (1986). Article  CAS  ADS  Google Scholar  * Fedorov, F. I. Theory of total reflection. Dokl. Akad. Nauk SSSR 105, 465–468 (1955). MathSciNet  Google Scholar  * Imbert, C.

Calculation and experimental proof of the transverse shift induced by total internal reflection of a circularly polarized light beam. Phys. Rev. D 5, 787 (1972). Article  ADS  Google Scholar

  * Onoda, M., Murakami, S. & Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004). Article  ADS  Google Scholar  * Onoda, M., Murakami, S. & Nagaosa, N. Geometrical

aspects in optical wave-packet dynamics. Phys. Rev. E 74, 066610 (2006). Article  ADS  MathSciNet  Google Scholar  * Bliokh, K. Y. Geometrodynamics of polarized light: Berry phase and spin

Hall effect in a gradient-index medium. J. Opt. A: Pure Appl. Opt. 11, 094009 (2009). Article  ADS  Google Scholar  * Hosten, O. & Kwiat, P. Observation of the spin Hall effect of light

via weak measurements. Science 319, 787–790 (2008). Article  CAS  ADS  Google Scholar  * Aiello, A. & Woerdman, J. Role of beam propagation in goos–hänchen and imbert–fedorov shifts.

Opt. Lett. 33, 1437–1439 (2008). Article  CAS  ADS  Google Scholar  * Shitrit, N., Bretner, I., Gorodetski, Y., Kleiner, V. & Hasman, E. Optical spin hall effects in plasmonic chains.

Nano Lett. 11, 2038–2042 (2011). Article  CAS  ADS  Google Scholar  * Ling, X. et al. Giant photonic spin hall effect in momentum space in a structured metamaterial with spatially varying

birefringence. Light Sci. Appl. 4, e290 (2015). Article  Google Scholar  * Yu, N. et al. Light propagation with phase discontinuities: generalized laws of reflection and refraction. Science

334, 333–337 (2011). Article  CAS  ADS  Google Scholar  * Yin, X., Ye, Z., Rho, J., Wang, Y. & Zhang, X. Photonic spin Hall effect at metasurfaces. Science 339, 1405–1407 (2013). Article

  CAS  ADS  Google Scholar  * Bliokh, K. Y. & Freilikher, V. Topological spin transport of photons: Magnetic monopole gauge field in Maxwell’s equations and polarization splitting of

rays in periodically inhomogeneous media. Phys. Rev. B 72, 035108 (2005). Article  ADS  Google Scholar  * Ritchie, N., Story, J. & Hulet, R. G. Realization of a measurement of a weak

value. Phys. Rev. Lett. 66, 1107 (1991). Article  CAS  ADS  Google Scholar  * Dennis, M. R. & Götte, J. B. The analogy between optical beam shifts and quantum weak measurements. New J.

Phys. 14, 073013 (2012). Article  ADS  Google Scholar  * Jayaswal, G., Mistura, G. & Merano, M. Observation of the Imbert–Fedorov effect via weak value amplification. Opt. Lett. 39,

2266–2269 (2014). Article  CAS  ADS  Google Scholar  * Töppel, F., Ornigotti, M. & Aiello, A. Goos–Hänchen and Imbert–Fedorov shifts from a quantum-mechanical perspective. New J. Phys.

15, 113059 (2013). Article  ADS  Google Scholar  * Gorodetski, Y. et al. Weak measurements of light chirality with a plasmonic slit. Phys. Rev. Lett. 109, 013901 (2012). Article  CAS  ADS 

Google Scholar  * Dressel, J., Malik, M., Miatto, F. M., Jordan, A. N. & Boyd, R. W. Colloquium: Understanding quantum weak values: Basics and applications. Rev. Mod. Phys. 86, 307

(2014). Article  ADS  Google Scholar  * Kofman, A. G., Ashhab, S. & Nori, F. Nonperturbative theory of weak pre-and post-selected measurements. Phys. Rep. 520, 43–133 (2012). Article 

ADS  MathSciNet  Google Scholar  * Ghosh, A. & Fischer, P. Chiral molecules split light: reflection and refraction in a chiral liquid. Phys. Rev. Lett. 97, 173002 (2006). Article  ADS 

Google Scholar  * Lee, Y. U. et al. Electro-optic switching in phase-discontinuity complementary metasurface twisted nematic cell. Opt. Express 22, 20816–20827 (2014). Article  CAS  ADS 

Google Scholar  Download references ACKNOWLEDGEMENTS This work was supported by the Ministry of Science, ICT and Future Planning (2014M3A6B3063706, 2015001948). The authors are grateful to

Ji-Hyun Lee at the Daejeon Center of the Korea Basic Science Institute for a focused ion beam (Quanta 3D FEG) milling fabrication of samples. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS *

Department of Physics and Quantum Metamaterials Research Center, Ewha Womans University, Seoul, 03760, Korea Y.U. Lee & J.W. Wu Authors * Y.U. Lee View author publications You can also

search for this author inPubMed Google Scholar * J.W. Wu View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Y.U.L. and J.W.W. are responsible

for an original idea and the design of experiment. Y.U.L. performed the numerical simulations and experimental measurements. Y.U.L. and J.W.W. wrote the manuscript. ETHICS DECLARATIONS

COMPETING INTERESTS The authors declare no competing financial interests. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS This work is licensed under a

Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated

otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To

view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Lee, Y., Wu, J. Control of optical spin Hall

shift in phase-discontinuity metasurface by weak value measurement post-selection. _Sci Rep_ 5, 13900 (2015). https://doi.org/10.1038/srep13900 Download citation * Received: 02 April 2015 *

Accepted: 03 August 2015 * Published: 10 September 2015 * DOI: https://doi.org/10.1038/srep13900 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this

content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative