Reader TTS

ABSTRACT The theory of proof-of-principle triple-mode squeezing is proposed via spontaneous parametric six-wave mixing process in an atomic-cavity coupled system. Special attention is

focused on the role of dressed state and nonlinear gain on triple-mode squeezing process. Using the dressed state theory, we find that optical squeezing and Autler-Towns splitting of cavity

mode can be realized with nonlinear gain, while the efficiency and the location of maximum squeezing point can be effectively shaped by dressed state in atomic ensemble. Our proposal can

find applications in multi-channel communication and multi-channel quantum imaging. SIMILAR CONTENT BEING VIEWED BY OTHERS GENERATION OF TWO MODE MECHANICAL SQUEEZING INDUCED BY

NONDEGENERATE PARAMETRIC AMPLIFICATION Article Open access 08 November 2024 THE ROLE OF TUNABLE NONLINEAR DARK RESONANCES ON VACUUM RABI SPLITTING AND OPTICAL BISTABILITY IN AN ATOM-CAVITY

SYSTEM Article Open access 18 May 2021 NOON-STATE INTERFERENCE IN THE FREQUENCY DOMAIN Article Open access 15 April 2024 INTRODUCTION Generating squeezed vacuum and entanglement with

controllable quantum states is important to quantum communication, quantum information processing and quantum computation1,2,3. For example, the single-mode quadrature squeezed state is used

for gravity wave detection, which is produced by the highly refined optical parametric oscillators (OPOs)4. The linear optical processing of single-beam quadrature squeezed states is used

for the continuous-variable quantum computing5,6. The multi-spatial mode squeezed light is desirable to continuous-variable quantum image processing techniques7,8. Generally speaking,

techniques for producing the squeezing states are based on either parametric down conversion in solid state crystal or spontaneous parametric four-wave mixing (SP-FWM) schemes in atomic

vapors. Traditionally, biphotons generated from Spontaneous parametric down-conversion (SPDC) in nonlinear crystals have very wide bandwidth (THz) and ultra-short coherence time (ps)9,10.

Using four-wave mixing (FWM) in sodium vapor, squeezed state of light was experimentally implemented11,12,13, however, achieving higher degree of squeezing via FWM in atomic vapors is

limited by spontaneous emission noise. Recently, researches on FWM in atomic vapors demonstrated that the spontaneous emission noise can be reduced or eliminated by using of

electromagnetically induced transparency (EIT)14. In EIT window the transmission1, slowing down15,16,17 and storage and retrieval18,19 of squeezed states were also experimentally

demonstrated. Nowadays, the interest to generate triple-mode squeezing is mainly due to its applicability in quantum information and communication20,21 where the field fluctuations in one of

the quadratures are reduced below the vacuum noise level and can be used in overcoming the shot-noise precision restrictions in optical measurements22 and enhancing the capacity of

communication channels23. Usually, signal-to-noise ratio is very low for six-wave mixing (SWM) in atomic vapor. However, by employing two-photon Doppler-free configurations as well as EIT,

enhanced nonlinear processes due to atomic coherence have been experimentally demonstrated24. The essentials of such enhanced nonlinear optical processes are the enhanced nonlinear

susceptibility due to atomic coherence, slowed light beam propagation in the atomic medium and greatly reduced linear absorption of the generated optical field due to EIT, which enable us to

investigate the topological photonic problems in atomic ensembles25,26. In our previous studies, distinctly different from and advantageous over the previously reported27, highly efficient

FWM, SWM and eight-wave mixing processes was experimentally demonstrated in an open-cycle Y-type atomic system. By manipulating the atomic coherence and multi-photon interferences among

different energy levels, we also demonstrated that the third-order and fifth-order nonlinear processes can coexist in open (such as V-type, Y-type and inverted Y-type) atomic systems24 and

the SWM signal can be comparable with or even greater than the FWM signal in amplitude. Such coexisting processes allow us to investigate spatial-temporal coherent interference between

third-order and fifth-order nonlinear processes. We also demonstrated the parametrically amplified FWM (PA-FWM) and parametrically amplified SWM (PA-SWM) processes. Such enhanced nonlinear

process28 is used to generate the strongly correlated bright twin or triple-mode bright beams in cavity and free space with high efficiency and narrow band width. In this paper, by applying

dressed state theory, we examine the influence of dressed state and nonlinear gain on the triple-mode squeezing via three-mode cone emission of SP-SWM and single-mode and two-mode squeezing

via degenerate and nondegenerate self-diffraction (or phase-conjugate) cone emissions of SP-FWM. It is indicated that the optical squeezing and nonlinear Autler-Towns (AT) splitting of

quantum noise can be achieved via nonlinear gain. The profiles and location of maximum squeezing point can be effectively modulated by dressed state, that can be achieved only in atomic

media. The triple-mode squeezing state proposed in current work can be directly used in multichannel quantum imaging. The quality of imaging (e.g. the contrast and resolution) is

significantly improved, compared with that obtained by using the two-mode squeezing state. In addition, the work can be used as implementation of triple-mode entangled source, where the

generation efficiency of entangled triple-beam and degree of entanglement will be significantly enhanced by nonlinear susceptibility and quantum gain. Therefore, our scheme can be also used

to achieve multi-channel communication. Finally, by using SP-SWM both in cold and hot atomic ensembles, narrow-band triple-photons with a long coherence time is realized. Such a long

coherence time may allow us to access and manipulate the squeezed state directly and has potential application in the long-distance quantum communication. So our scheme has following

advantages. First, due to the near- and on-resonance nonlinear optical processes can be enhanced by atomic coherence technique, so the generation efficiency of SP-SWM and degree of triple of

squeezing (entanglement) can be significantly enhanced by manipulating nonlinear susceptibility and quantum gain. Second, due to EIT window (MHz), not only the resonance absorption is

eliminated, but narrow bandwidth signals at low light level is obtained as well. So compared with correlated photon pairs from SPDC, which have characteristics of very wide bandwidth (THz)

and ultra-short coherence time (ps). Our scheme has a narrower-bandwidth (MHz) and longer coherence time (0.1–1.0 _μs_). Last but not least, the quality of imaging can be well controlled by

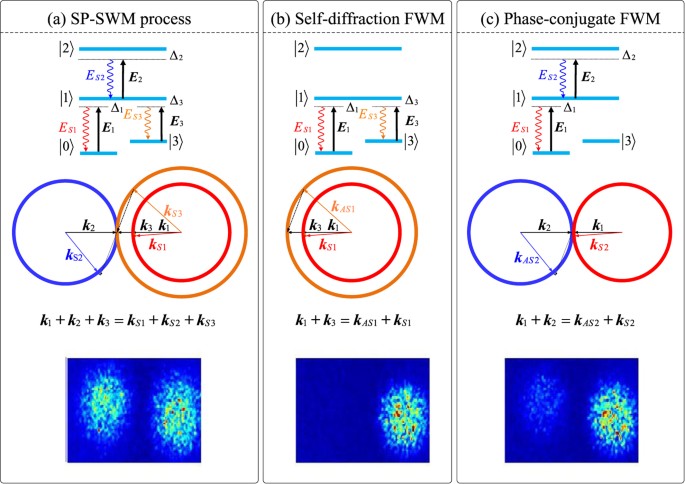
multiple parameters. BASIC THEORY OF TRIPLE-MODE CONE EMISSION A theoretical scheme for the preparation triple-mode by SP-SWM is carried out in 85Rb atomic ensemble. As shown in Fig. 1(a),

the energy levels of 5S1/2(F = 3), 5P3/2(F = 3), 5D5/2 and 5S1/2(F = 2) forming the reverse Y-type four-level atomic system29 are corresponding to , , and , respectively. In this energy

level system, three high intensity pumping fields , and are used to coupling with , and , respectively. Therefore, non-degenerate SP-SWM process is excited and three quantum correlated

signals _E__S_1, _E__S_2 and _E__S_3 are generated, satisfies the phase-matching condition k1 + k2 + k3 = ks1 + ks2 + ks3, as the phase-matching ring configuration shown in Fig. 1(a). In

this reverse Y-type system, via the perturbation chain , the density matrix element for the generated signal _E__S_1 can be obtained as where is the Rabi frequency, here μ_ij_ is electric

dipole moment between energy state and and is the transverse decay rate, d10 = Γ10 + iΔ1, , and . Similarly, we can obtain and for _E__S_2 and _E__S_3 via the perturbation chains and

respectively and the corresponding expressions for _E__S_2 and _E__S_3 are where is Rabi frequency of _E__Si_(_i_ = 1, 2, 3), δ_i_ is small fluctuation around ω_j_ (i = 1, 2, 3 j = S1, S2,

S3), with . , , , , and . Furthermore, the nonlinear gain is proportional to the corresponding density matrix elements . The fluctuations of the triple-modes _E__S_1, _E__S_2 and _E__S_3

generated here have zero on average and quantum correlated with each other, That is to say, if there is no seeding to this SP-SWM process, the output states are the triple-mode squeezed

vacuum states. By adjusting one of the SP-SWMs, the other two will be affected. For the SP-SWM, as shown in Fig. 2(a), any one of the three polar angles (φ_S_1, φ_S_2 or φ_S_3) can be

represented by the other two and we cannot get the dependent phase mismatching conditions for _E__S_1, _E__S_2 or _E__S_3, which is much more complex than the self-diffraction and

phase-conjugate SP-FWM cases. In order to investigate the quantum-correlated of three-photon cone emissions, we fix the polar angle of _k__s_2 to be , which makes the other two polar angles

(φ_s_1 and φ_s_3) to be fixed relatively. According to the configuration shown in Fig. 2(a), we can get the phase mismatching conditions for _E__S_1 and _E__S_3 as following, As we know that

the fifth-order nonlinear susceptibility highest if the incident light is set collinear , so the nonlinear conversion efficiency is the highest as collinear. However, the generated SP-SWM

is buried in strong fluorescence background due to the resonance fluorescence signal is also strongest in this direction. To ensure high conversion efficiency of SP-SWM and suppressed

collinear resonance fluorescence, so we set . By setting , now we can investigate SP-SWM three-mode cone emission based on Eqs (1, 2, 3, 4, 5) and the main results are shown in Fig. 2(b).

According to the requirements spatial phase matching conditions discussed in Fig. 2(a), _E__S_3 (the outer cones) and _E__S_1 (inner cones) propagate along the same direction (the right-hand

side ones) and the cones of _E__S_2 propagate along the opposite directions respect to _E__S_1 and _E__S_3 (the left-hand side one). In light that _E__S_2 is set at the place with the

highest emission efficiency intentionally (Δ_k__s_2 = 0 at ), we only display the phase mismatching conditions and the normalized generation efficient of k_s_1 and k_s_3, which are in Fig.

2(c,d), respectively. According to Eqs (4 and 5), we display the phase mismatching Δ_k__s_1,_s_3 versus transverse coordinates x and y at z = 10 m in Fig. 2(c). It is clear to see that x and

y located in a circle is corresponding to Δ_k__s_1,_s_3 = 0, where the six beams are completely phase matching, leading to the largest efficiency to generate the SP-FWMs. However, as x and

y deviate the circle, the generation coefficient of the SP-FWMs will reduce greatly for Δ_k__s_1,_s_3 ≠ 0. Therefore, the intensities of _E__S_1 and _E__S_3 are the largest on the circle and

decrease sharply deviate from the circle. To make this problem clearly, we display the normalized generation efficient in Fig. 2(d). It can be seen that the peaks of the normalized

generation efficient are on the circles which coincide with the circles Δ_k__s_1,_s_3 in Fig. 2(c). When the propagation distance change, the radii of the circles are also increased

monotonously, so we can obtain the circles enlarged along with the increment of propagation distance as shown in Fig. 2(b). The measured intensity of _E__S_3 and _E__S_1 versus Δ1 in such

SP-SWM process is shown in Fig. 2(e1,e2), where Fig. 2(e1) is measured intensity of _E__S_1 (85_Rb_, _F_ = 3→_F′_ transition) and Fig. 2(e1) is measured intensity of _E__S_2 (85_Rb_, _F_ = 

2→_F′_ transition). On the other hand, a self-diffraction FWM process will be generated in the lambda-type sub-system if only _E_1 and _E_3 are used to driving and , respectively. As shown

Fig. 1(b), the cone emissions of _E__S_1 and _E__AS_1 propagate along the same direction through the medium as the requirement of the phase-matching conditions k1 + k3 = k_S_1 + k_AS_1. As

_E__S_1 and _E__AS_1 in Fig. 1(b) behave like triple-mode SP-SWM if the generated _E__S_2 is removed, therefore, the phase mismatching Δ_k__S_1,_AS_1 and normalized generation efficient also

exhibit similar behaviors. In this lambda-type subsystem, via the pathway and considering the dressing effect of _E_3, the density matrix element for _E__S_1 is where d20 = Γ20 + i(Δ1 + 

Δ2), d30 = Γ30 + iδ, , and δ is small fluctuation around ω_i_, with (i = S1, AS1, S2, AS2). Similar to , we can obtain the density matrix element for via the pathway as where d01 = Γ01 − 

i(Δ3 + δ), d02 = Γ02 − i(Δ3 + δ + Δ2), d03 = Γ03 − iδ), d13 = Γ13 + i(Δ1 − δ) and d23 = Γ23 + i(Δ1 + Δ2 − δ). However, if only _E_1 and _E_2 are applied to driving and in the ladder-type

sub-system (Fig. 1 (c)), respectively, a phase-conjugate FWM process will be occurred. Different from the self-diffraction FWM cone emission, the phase conjugate FWM cone emissions propagate

along the opposite directions for the phase-matching conditions k1 + k2 = k_S_2 + k_AS_2 (Fig. 1 (c)). And the radii of the circles increase along the increment of the propagation distance,

which make the k_S_2 and k_AS_2 cones form along the positive and negative propagation directions, respectively. In this ladder-type sub-system , via the pathway and considering the

dressing effect of _E_3, the density matrix element for _E__AS_2 can be written as where , and . Similarly, the density matrix element for _E__S_3 can be also obtained via the pathway :

where d21 = Γ21 + i(δ + Δ2) and d23 = Γ23 + i(Δ2 ± Δ3 + δ). The measured spots corresponding to SP-SWM, phase-conjugate FWM, self-diffraction FWM are shown in the bottom of Fig. 2(a–c),

respectively. When there is no seeding to those SP-FWM process (both self-diffraction FWM and phase-conjugate FWM), the output states are the two-mode squeezed vacuum states and the

generated signals are quantum correlated. Before going to next section, let us pay attention on the comparison between our SP-SWM models and standard FWM scheme. In our theoretical model,

SP-SWM process is used to generate quantum correlated triple-mode beams, such process can be considered as the cascading the phase-conjugate FWM and self-diffraction FWM. To be more

specific, when pumping fields _E_1 with intensity _I_1 is seeded into atomic ensemble and coupled with , for a gain G created by _E_2, twin beams _E__S_1 and _E__AS_1 are simultaneously

generated via the self-diffraction FWM process. The intensities of these twin beams _E__S_1 and _E__AS_1 are _I__S_1 = _GI_1 and _I__AS_1 = (_G_ − 1)_I_1, respectively. Although the total

power of the twin beams _E__S_1 and _E__AS_1 are significantly amplified, the variance of the relative intensity difference _I__S_1 − _I__AS_1 between them remains unchanged after the

amplification. As a result, the relative intensity difference of beams _E__S_1 and _E__AS_1 is squeezed compared with the corresponding shot noise limit (SNL) by an amount of 1/(2_G_ − 1).

Then, one of the twin beams (say _E__S_1 as shown in Fig. 1(b)) is involved in a phase-conjugate FWM, where the output beam _E__S_2 is amplified and a conjugate beam (_E__AS_1) is

simultaneously generated for gain _G_ created by _E_3. The intensities of these two newly generated twin beams (_E__S_2 and _E__AS_1) are _I__S_2 = _G_2_I_1 and _I__AS_2 = _G_(_G_ − 1)_I_1,

respectively. If one calculates the intensity-difference noise of the three generated beams (_E__AS_1, _E__S_1 and _E__AS_2), given by _I__S_2 − _I__AS_2 − _I__S_1 and compares it with the

corresponding SNL, one will find that the degree of intensity-difference squeezing of the triple beams is given by 1/(2_G_2 − 1) and the amount of squeezing in our triple-mode case is

significantly increased compared with two-mode squeezing. As a matter of fact, the SP-SWM is generated from internal cascading the self-diffraction and phase-conjugate FWM. Compared with the

single self-diffraction or phase-conjugate FWM, the amount of squeezing from SP-SWM is increased from 1/(2_G_ − 1) to 1/(2_G_2 − 1) due to such cascading effect. In other words, by

increasing the number of quantum modes, the quantum correlation is also enhanced in our system. Another advantage of our system is the phase insensitivity that makes it possible to easily

extend our system to a large number of modes, as it does not require relative phase stability between all the parametric amplification processes. MULTI-MODE SQUEEZING IN RING CAVITY Now we

theoretically study optical squeezing via multi-wave mixing (MWM) process in an atomic ensemble-cavity coupled system. As shown in Fig. 3, here the ring cavity is formed by four mirrors with

a longitudinal cavity length 17 cm. The mirrors M3 and M1 are input and output mirrors with a radius of 50 mm and the reflectance r3 (r1) and transmittance t3 (t1) coefficient fulfill the

constraint condition (i = 1, 3), while M2 and M4 are highly reflection mirrors. Cavity mode scanning and locking can be implemented by a piezoelectric transducer (PZT) behind M4. The length

of the atomic vapor cell with the Brewster windows is La = 7 cm, where the atomic vapor cell is wrapped in μ-metal sheets to shield from external magnetic fields and a heat tape is placed

outside the sheets for controlling the temperature. Since we do not consider Doppler effects in this paper, our analysis is also suitable for standing-wave cavity. For the limit of cavity,

the conical emission is disappeared. However, if paired photons or three photons are prepared simultaneously, the squeezing between them still exists. Now, we apply the basic theory to study

optical squeezing via MWM process. The quadrature amplitude summations components and quadrature phase summations components are plotted in Fig. 4 by scanning Δ/(γ + γ_c_) at different

Δ1/(γ + γ_c_), where Fig. 4(a,c,e) are quadrature amplitude summations , and and Fig. 4(b,d,f) are the quadrature phase summation , and , respectively. In Fig. 4, the dotted-line is obtained

by blocking the pump fields so as the fifth-order nonlinear process is not active and the first solid curve in each panel is obtained by injected squeezed vacuum states to cavity and the

atomic coupling system, all those (dotted-line and the first solid curve in each panel) can be used as a baseline to examine the effect of the nonlinear process inside cavity on the output

states. Compared with the squeezed vacuum states, we can see from Fig. 4(b,e) that the variance of quadrature amplitude summation and quadrature phase summation are far below the shot-noise

limit (SNL) as well as the first solid curve in each panel in a wide frequency range of Δ1/(γ + γ_c_). Therefore, it is enough to assert that and are further squeezed for the influence of

fifth-order nonlinear gain. However, the variance of and becomes noisier than the input squeezed states, as shown in Fig. 4(a,f), for almost all curve are above the SNL. This phenomenon is

in line with Heisenberg uncertainty relationship, if the quantum noise variance of quadrature amplitude (Fig. 4(a)) becomes noisier, the variance of quadrature phase (Fig. 4(b)) will be

squeezed and vice versa as shown in Fig. 4(e,f). On the other hand, we can see from of Fig. 4(a,c) that the evolutions of the quadrature amplitude noise variances and show an AT-splitting

(the dashed curve). and the noisy degree are amplified, which is different from Fig. 4(e). The main difference can be explained by the interaction Hamiltonian describing the SP-SWM process,

where the generation of any two photons and were accompanied by the annihilation a probe photon . Therefore, in this nonlinear SP-SWM process, and have similar quantum characteristics, which

is different from . In other words, and () in competition with each other. Contrary to this, for and have similar quantum characteristics, the noisy degree is significantly squeezed for

anti-amplification of nonlinear gain. In addition, with the sequential (or nested)-cascade type of double dressing as well as and () have different quantum characteristics, the tri-peak AT

structure of each curve in Fig. 4(a,c) are observed and the noisy degree of and are enhanced for amplification of nonlinear gain. These results indicate that the squeezing degree or the

noisy degree can be effectively modulated by the nonlinear gain κ_S_ as well as the quantum characteristics of the triple-mode. We now consider the self-diffraction SP-FWM (Fig. 1 (b))

process in the ring cavity shown in Fig. 3, where the generated SP-FWM signals _E__S_1 and _E__AS_1 are propagate along the cavity axis with the same direction forming two cavity modes and

detected by one APD device. As the polarizations of two modes are perpendicular, one can record them independently by putting a polarizer before the APD device and rotating it. On the other

hand, in the phase-conjugate SP-FWM process, these two SP-FWM signals will form two modes with different directions, which can be detected by two APD devices. Although the phase-conjugate

and self-diffraction SP-FWM are described by different nonlinear coefficient κ1 and κ2, respectively, these SP-FWM signals (both the phase-conjugate and self-diffraction) have the similar

quantum characteristics except propagation along different directions. Therefore, the motion equations of such two SP-FWM signals can be written with unified form. where and are the coupled

vacuum modes. Considering the Fourier transform of Eqs (10 and 11) and boundary condition , the quantum noise variance of quadrature amplitude summation and quadrature phase summation at

output can be investigated by scanning Δ/(γ + γ_c_) and Δ1/(γ + γ_c_) simultaneously. To invest noise fluctuation of cavity mode under various injection fields, here EPR field and coherent

field is injected into the ring cavity to make a comparison. Firstly, we adopt coherent fields as the injected fields. The quantum noise variances of and are illustrated in Fig. 5(a1,a2),

respectively. From Fig. 5(a1,a2), we can see that only is lower than SNL as Δ1/(γ + γ_c_) scanned from negative to positive, where the maximum squeezing is corresponding to the location of

reverse AT splitting created by _E_2, that is, the position of the dark state. While, the quantum noise variances of become noisier as Δ1/(γ + γ_c_) is scanned in the vicinity of the dressed

state. On the other hand, except without considering the dressing effect from _E_2, other conditions in Fig. 5(b1,b2) are same as those in Fig. 5(a1,a2), respectively. In comparison with

the cases with and without dressing effect of _E_2, the AT splitting in quadrature amplitude and the reverse AT splitting in quadrature phase are disappears and the location of maximum

noisier and squeezing are moved to Δ1/(γ + γ_c_). We can see that the dressed state can effectively control the squeezing process. Therefore, the influence of the AT splitting of _E_2 on the

squeezing is obvious. Then, by setting Δ1/(γ + γ_c_) = 15 (Fig. 6(a1–a2,b1–b2)) and Δ1/(γ + γ_c_) = 0 (Fig. 6(c1–c2,d1–d2)), respectively and scanning Δ/(γ + γ_c_) as well as Δ2/(γ + γ_c_)

synchronously, the suppression and enhancement role of dressed state on the quantum noise variance of and are studied. In the case of Δ1/(γ + γ_c_) = 15, as shown in Fig. 6(a1), the quantum

noise variance of becomes noisier and no squeezing when Δ1/(γ + γ_c_) is scanned from positive to negative. Specifically speaking, the noise fluctuation of is significantly enhanced in the

region Δ2 < 0 and suppressed in the region Δ2 > 0, which is corresponding enhancement () and suppression (Δ1 = Δ2 = 15) conditions of the dressed state, respectively. It should be

emphasized that is still no squeezing in suppression region Δ2 > 0 for the curve is above the SNL. However, the situation is exactly the opposite in terms of the quadrature phase

summation, as shown in Fig. 6(a2), where the profiles of quantum noise variances show that is squeezed when Δ2/(γ + γ_c_) is scanned and the degree of squeezing get its maximum in the region

Δ2 < 0. Fig. 6(b1,b2) are same as those in Fig. 6(a1,a2) except without considering the dressing effect from _E_2. In comparison the cases with and without _E_2, the quantum noise

variances of the and is unchanged as Δ2/(γ + γ_c_) is scanned. For the case Δ/(γ + γ_c_) = 0, we take the same method to study the influence of dressed state on two-mode squeezing. As shown

in Fig. 6(c1,c2), the quantum noise variances of the and at Δ = 0 exhibit a pure suppression and a pure enhancement, respectively. It is worth mentioning that the suppression conditions are

all Δ1 = Δ2. If the dressing effect of _E_2 can be neglected, the quantum noise variances are also not affected as shown in Fig. 6(d1,d2). It is clear see that two-mode squeezing can be

effectively controlled by the suppression and enhancement of dressed state. Finally, the influence of dressed state on the squeezing with Einstein-Podolsky-Rosen (EPR) fields injected is

shown in Fig. 7(a1–a2), where Δ/(γ + γ_c_) and Δ2/(γ + γ_c_) are scanned with Δ1/(γ + γ_c_) = 15. As shown in Fig. 7(a1), the variance of becomes noisier when Δ2/(γ + γ_c_) is scanned from

positive to negative and the profile of the variances (showing enhancement in Δ2 < 0 and suppression in Δ2 > 0) is same as the situation when coherent fields injected is considered. In

addition, although is injected with squeezed fields and suppressed at Δ2 > 0, there is no squeezing in all region. As mentioned above, for the influence of dressed state as well as

injected with squeezed fields, the variance of shown in Fig. 7(a2) is significantly squeezed compared with the injecting coherent fields. To be specific, get its maximum squeezing value at

and minimum squeezing value at Δ1 = Δ2 = 15. On the other hand, the quantum noise variances of the and do not change versus Δ1/(γ + γ_c_) if the dressing effect from is absent. However, and

shown in Fig. 7(b1,b2) have a higher squeezing level than those shown in Fig. 6(b1,b2) for injected with squeezed fields. It is worth mentioning that our scheme has following advantages.

First, due to the near- and on-resonance nonlinear optical processes can be enhanced by atomic coherence technique, so the generation efficiency of SP-SWM and degree of triple of squeezing

(entanglement) can be significantly enhanced by manipulating nonlinear susceptibility and quantum gain. Second, due to electromagnetically induced transparency (EIT) window (MHz), not only

the resonance absorption is eliminated, but narrow bandwidth signals at low light level is obtained as well. So compared with correlated photon pairs from SPDC, which have characteristics of

very wide bandwidth (THz) and ultra-short coherence time (ps). Our scheme has a narrower-bandwidth (MHz) and longer coherence time (0.1–1.0 _μs_). Last but not least, the quality of imaging

can be well controlled by multiple parameters. CONCLUSION In summary, we have theoretically investigated the multi-mode quantum noise squeezing and amplification with MWM signals in a ring

cavity filled with rubidium vapors. It is found that the squeezing and amplification of quantum noise can be effectively modulated by dressed state and nonlinear gain coefficient.

Specifically, nonlinear gain leads to the optical squeezing as well as nonlinear AT splitting of cavity mode and dressed state can be used to reshape the efficiency as well as the location

of maximum squeezing point. In optical squeezing, the physical properties of dressed state and nonlinear gain are quite similar. It is worth mentioning that our system has following

advantages, first, the amount of squeezing from SP-SWM is significantly improved compared with self-diffraction and phase-conjugate FWM. Second, intensity-difference squeezing from SPDC has

the characteristics of very wide bandwidth (THz) and ultra-short coherence time (ps), however, a narrower-bandwidth (MHz) and longer coherence time (0.1–1.0 _μs_) is implemented from SP-SWM.

Such as long coherence time allows us to access and manipulates the spatial squeezing directly. Third, intensity-difference squeezing can be well controlled by multiple parameters. One of

the main advantages of our system is that can be directly used in multichannel quantum imaging and the quality of imaging, including the contrast and resolution, is significantly improved

compared with the two-mode squeezing state. The proposed method is also used as implementation of triple-mode entangled source to achieve multi-channel communication. THEORETICAL MODELS In

this part, a new scheme via fifth-order nonlinear channels to produce triple mode squeezed state is proposed as shown in Fig. 3, where _E_1, _E_2 and _E_3 are injected into the ring cavity

and coupled to , and , respectively. Considering the assumption that the fields _E_2 and _E_3 are much larger than the probe _E_1, two SWM (_E__S_1 and _E__S_3) photons are generated, which

is accompanied by the annihilation a probe photon _a_1 and three pumping field photon with phase matching condition satisfy k_S_1 = k1 + k2 − k2 + k3 − k_S_3 and k_S_3 = k1 + k3 − k_S_1 + k2

 − k2. In this process, _E_1, _E__S_1 and _E__S_3 are treated as quantum fields, while _E_2 and _E_3 are considered as classical fields, therefore, the interaction Hamiltonian describing

this process can be expressed as , where , and are the annihilation operator of triple cavity modes _E_1, _E__S_1 and _E__S_3. The fifth-order nonlinear coefficients κ_S_ described by the

nonlinear gain in SWM processes, is proportional to . On the other hand, the Hamiltonian for the probe field is , where ε1 is the amplitude of the probe field. Therefore, taking into account

the loss and nonlinear gain, we can obtain the equations for three cavity modes as following: where Δ is the cavity detuning, , and denote the injected fields at _E_1, _E__S_1 and _E__S_3

channels, respectively. , and are the vacuum modes coupled with the corresponding cavity modes , and and γ1, γ_S_1 and γ_S_3 denote the dimensionless damping rate which are related to the

amplitude reflection and transmission coefficients of the input and output couplers of the optical cavity. Without loss of generality, one can decompose the system variables (including the

resonant cavity modes, the injected fields and vacuum modes) into their steady-state values and small fluctuations around the steady-state values, for instance, , , (i = 1, S1, S3), where

α_i_, and α_ci_ indicate the mean values of the corresponding fields and , and demonstrate small fluctuations around the steady-state values. The injected probe field is a coherent field and

its fluctuations are the same as the vacuum fluctuations, so . However, the generated cavity modes and coupled vacuum modes have zero mean values, i.e., and . The steady-state solutions can

be obtained by letting _dα__i_/_dt_ = 0 (_i_ = 1, _S_1, _S_3) and throwing away the vacuum fluctuations as well as the cavity detuning in Eqs (12, 13, 14). Therefore, the steady state value

of the triple cavity mode satisfies the following equations In order to simplify the calculation, we assume that , and are nearly frequency degenerate, leading damping rates to be identical

(γ1 = γ_S_1 = γ_S_3), Now, the steady-state values of of triple cavity modes have following value: By means of linearized analysis procedure, small fluctuations around of triple cavity mode

can be obtained, Now, we need the fluctuations of quadrature amplitude () and quadrature phase () components to study squeezing characteristics between triple modes. Considering the Fourier

transform of the operators, Eqs (20, 21, 22) can be recasted in terms of the quadrature amplitude and phase operators: where Ω is the analysis frequency. Now, these equations can be solved

in the frequency domain under the boundary condition and the spectra of squeezing characteristics between triple modes in terms of the input fluctuation can be obtained analytically. Whats

more, the fluctuations of quadrature amplitude summation is same as the quadrature phase difference of any two output modes and the quadrature amplitude difference is same as the quadrature

phase summation of any two output modes, therefore, we will investigate the triple modes squeezing by means of amplitude and quadrature phase summation. ADDITIONAL INFORMATION HOW TO CITE

THIS ARTICLE: Wen, F. _et al._ Triple-mode squeezing with dressed six-wave mixing. _Sci. Rep._ 6, 25554; doi: 10.1038/srep25554 (2016). REFERENCES * Akamatsu, D., Akiba, K. & Kozuma, M.

Electromagnetically Induced Transparency with Squeezed Vacuum. Phys. Rev. Lett. 92, 203602 (2004). Article  ADS  Google Scholar  * Braunstein, S. L. & van Loock, P. Quantum information

with continuous variables. Rev. Mod. Phys. 77, 513–577 (2005). Article  ADS  MathSciNet  Google Scholar  * Bowen, W. P. et al. Experimental investigation of continuous-variable quantum

teleportation. Phys. Rev. A 67, 032302 (2003). Article  ADS  Google Scholar  * Vahlbruch, H. et al. Observation of Squeezed Light with 10-dB Quantum-Noise Reduction. Phys. Rev. Lett. 100,

033602 (2008). Article  ADS  Google Scholar  * Aoki, T. et al. Experimental Creation of a Fully Inseparable Tripartite Continuous-Variable State. Phys. Rev. Lett. 91, 080404 (2003). Article

  ADS  Google Scholar  * Menicucci, N. C., Flammia, S. T. & Pfister, O. One-Way Quantum Computing in the Optical Frequency Comb. Phys. Rev. Lett. 101, 130501 (2008). Article  ADS  Google

Scholar  * Coelho, A. S. et al. Three-Color Entanglement. Science 326, 823–826 (2009). Article  ADS  CAS  Google Scholar  * Sokolov, I. V. & Kolobov, M. I. Squeezed-light source for

superresolving microscopy. Opt. Lett. 29, 703–705 (2004). Article  ADS  Google Scholar  * Burnham, D. C. & Weinberg, D. L. Observation of Simultaneity in Parametric Production of Optical

Photon Pairs. Phys. Rev. Lett. 25, 84–87 (1970). Article  ADS  CAS  Google Scholar  * Kwiat, P. G. et al. New High-Intensity Source of Polarization-Entangled Photon Pairs. Phys. Rev. Lett.

75, 4337–4341 (1995). Article  ADS  CAS  Google Scholar  * Slusher, R., Hollberg, L., Yurke, B., Mertz, J. & Valley, J. Observation of squeezed states generated by four-wave mixing in an

optical cavity. Phys. Rev. Lett. 55, 2409 (1985). Article  ADS  CAS  Google Scholar  * Qin, Z. et al. Experimental generation of multiple quantum correlated beams from hot Rubidium vapor.

Phys. Rev. Lett. 113, 023602 (2014). Article  ADS  Google Scholar  * Qin, Z., Cao, L. & Jing, J. Experimental characterization of quantum correlated triple beams generated by cascaded

four-wave mixing processes. Appl. Phys. Lett. 106, 211104 (2015). Article  ADS  Google Scholar  * Fleischhauer, M., Imamoglu, A. & Marangos, J. P. Electromagnetically induced

transparency: Optics in coherent media. Rev. Mod. Phys. 77, 633–673 (2005). Article  ADS  CAS  Google Scholar  * Akamatsu, D. et al. Ultraslow Propagation of Squeezed Vacuum Pulses with

Electromagnetically Induced Transparency. Phys. Rev. Lett. 99, 153602 (2007). Article  ADS  Google Scholar  * Hètet, G. et al. Delay of squeezing and entanglementusing electromagnetically

inducedtransparency in a vapour cell. Opt. Express 16, 7369–7381 (2008). Article  ADS  Google Scholar  * Arikawa, M. et al. Observation of electromagnetically induced transparency for a

squeezedvacuum with the time domain method. Opt. Express 15, 11849–11854 (2007). Article  ADS  CAS  Google Scholar  * Honda, K. et al. Storage and Retrieval of a Squeezed Vacuum. Phys. Rev.

Lett. 100, 093601 (2008). Article  ADS  Google Scholar  * Appel, J., Figueroa, E., Korystov, D., Lobino, M. & Lvovsky, A. I. Quantum Memory for Squeezed Light. Phys. Rev. Lett. 100,

093602 (2008). Article  ADS  Google Scholar  * Simon, C. et al. Quantum Repeaters with Photon Pair Sources and Multimode Memories. Phys. Rev. Lett. 98, 190503 (2007). Article  ADS  Google

Scholar  * Duan, L.-M., Lukin, M., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001). Article  ADS  CAS 

Google Scholar  * Grangier, P., Slusher, R., Yurke, B. & LaPorta, A. Squeezed-light–enhanced polarization interferometer. Phys. Rev. Lett. 59, 2153 (1987). Article  ADS  CAS  Google

Scholar  * Shapiro, J. H. Optical waveguide tap with infinitesimal insertion loss. Opt. Lett. 5, 351–353 (1980). Article  ADS  CAS  Google Scholar  * Zhang, Y., Anderson, B. & Xiao, M.

Efficient energy transfer between four-wave-mixing and six-wave-mixing processes via atomic coherence. Phys. Rev. A 77, 061801 (2008). Article  ADS  Google Scholar  * Zhang, Y. Q. et al.

Photonic Floquet topological insulators in atomic ensembles. Laser Photon. Rev. 9, 331–338 (2015). Article  ADS  CAS  Google Scholar  * Zhang, Y. Q., Liu, X., Belić, M. R., Wu, Z. K. &

Zhang, Y. P. Modulation of the photonic band structure topology of a honeycomb lattice in an atomic vapor. Ann. Phys. 363, 114–121 (2015). Article  ADS  MathSciNet  CAS  Google Scholar  *

Ma, H. & de Araujo, C. B. Interference between third-and fifth-order polarizations in semiconductor doped glasses. Phys. Rev. Lett. 71, 3649 (1993). Article  ADS  CAS  Google Scholar  *

Wen, F. et al. Multidressed suppression and enhancement of spontaneous parametric four-wave-mixing processes. J. Opt. Soc. Am. B 31, 2384–2389 (2014). Article  ADS  CAS  Google Scholar  *

Zhang, Y. Q. et al. Optical cavity squeezing of multiwave mixing via dark states. J. Opt. Soc. Am. B 31, 2792–2801 (2014). Article  ADS  CAS  Google Scholar  Download references

ACKNOWLEDGEMENTS This work was supported by the 973 Program (2012CB921804), NSFC (11474228, 61308015, 61205112), KSTIT of Shaanxi province (2014KCT-10), NSFC of Shaanxi province (2014JQ8341,

2014JZ020), XJTUTT(cxtd2014003), KLP of Shaanxi province (2013SZS04-Z02) and FRFCU(xjj2013089, xjj2014099, xjj2014119). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Key Laboratory for

Physical Electronics and Devices of the Ministry of Education & Shaanxi Key Lab of Information Photonic Technique, Xi’an Jiaotong University, Xi’an, 710049, China Feng Wen, Yiqi Zhang, 

Junling Che, Junling Che, Hasan Abdulkhaleq, Yanpeng Zhang & Hongxing Wang * School of Science, Xi’an Jiaotong University, Xi’an, 710049, China Feng Wen, Zepei Li & Hong Gao Authors

* Feng Wen View author publications You can also search for this author inPubMed Google Scholar * Zepei Li View author publications You can also search for this author inPubMed Google

Scholar * Yiqi Zhang View author publications You can also search for this author inPubMed Google Scholar * Hong Gao View author publications You can also search for this author inPubMed 

Google Scholar * Junling Che View author publications You can also search for this author inPubMed Google Scholar * Junling Che View author publications You can also search for this author

inPubMed Google Scholar * Hasan Abdulkhaleq View author publications You can also search for this author inPubMed Google Scholar * Yanpeng Zhang View author publications You can also search

for this author inPubMed Google Scholar * Hongxing Wang View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS F.W. wrote the main manuscript and

contributed to experimental analysis. H.W. and Y.Z. provided the idea. Z.L., Y.Z., H.G., J.C. and H.A. contributed to the presentation and execution of the theoretical work. All authors

discussed the results and contributed to the writing of the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests. RIGHTS AND PERMISSIONS

This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons

license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to

reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wen, F., Li, Z.,

Zhang, Y. _et al._ Triple-mode squeezing with dressed six-wave mixing. _Sci Rep_ 6, 25554 (2016). https://doi.org/10.1038/srep25554 Download citation * Received: 13 January 2016 * Accepted:

18 April 2016 * Published: 12 May 2016 * DOI: https://doi.org/10.1038/srep25554 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable

link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative