Reader TTS

ABSTRACT Supercapacitors (SCs) are a type of energy storage device with high power density and long lifecycles. They have widespread applications, such as powering electric vehicles and

micro scale devices. Working stability is one of the most important properties of SCs, and it is of significant importance to investigate the operational characteristics of SCs working under

extreme conditions, particularly during high-_g_ acceleration. In this paper, the failure mechanism of SCs upon high-_g_ impact is thoroughly studied. Through an analysis of the intrinsic

reaction mechanism during the high-_g_ impact, a multi-faceted physics model is established. Additionally, a multi-field coupled kinetics simulation of the SC failure during a high-_g_

impact is presented. Experimental tests are conducted that confirm the validity of the proposed model. The key factors of failure, such as discharge currents and discharging levels, are

analyzed and discussed. Finally, a possible design is proposed to avoid the failure of SCs upon high-_g_ impact. SIMILAR CONTENT BEING VIEWED BY OTHERS FATIGUE ANALYSIS OF AN ENERGY STORAGE

SUPERCAPACITOR BOX UNDER RANDOM VIBRATION LOADING Article Open access 04 March 2025 IMPACT-RESISTANT SUPERCAPACITOR BY HYDROGEL-INFUSED LATTICE Article Open access 01 August 2024 A

HIGH-SPEED CURRENT SOURCE FOR MAGNETORHEOLOGICAL APPLICATIONS Article Open access 16 October 2023 INTRODUCTION With the increasing concern for the worldwide energy crisis and environmental

pollution due to the depletion and burning of fossil fuels, there is an urgent demand for efficient, clean and sustainable energy sources. Supercapacitors or electrochemical capacitors

represent a promising approach to meet the increasing power needs of both macro and microelectronic devices1,2. Compared with other energy storage methods, supercapacitors offer advantages

such as high power density, good environmental adaptability and long cycle life3,4,5,6,7. To date, supercapacitors have been widely used as energy supplies for electric cars, subway trains

and satellites. For these practical applications, supercapacitors may suffer many extreme working conditions, and their reliability is a serious concern that needs to be taken into

consideration in application design and development. For example, the high-_g_ acceleration (high acceleration up to tens of thousands times that of gravity) often occurs during the

operation of electric cars, subway trains and satellites when they are speeding up, slowing down, turning, etc. As a result, the influences of high-_g_ acceleration must be considered in

order to insure normal and safe operation of these systems. There have been reports about the reliability of supercapacitors and other electrochemical energy storage devices, such as lithium

batteries, under high-_g_ acceleration impacts. According to these studies, supercapacitors may suffer voltage fluctuations while discharging during a high-_g_ impact8. However, the

previous reports for supercapacitor failure under high-_g_ impact are only based on experimental tests. Due to the lack of theoretical analysis, the kinetic mechanism of this failure

phenomenon is still unclear. To improve the reliability of supercapacitors during high-_g_ impacts, it is highly necessary to study the kinetic mechanism of this failure phenomenon. In this

paper, we focus on the electrical-chemical mechanism of the supercapacitor voltage fluctuation during a high-_g_ impact process. For the first time, a multi-field coupled kinetics model is

proposed to describe the failure mode during such a process. In this model, the electrolyte flow and ion redistribution caused by the high-_g_ impact account for the voltage fluctuation, and

the ion concentration field and electrical field during the impact process can be worked out completely by the model. Simulations of supercapacitor voltage and ion concentration response

processes are realized, and experimental tests are conducted using a Machete Hammer, which verify the model. Based on the failure mechanism characterized by the model, an optimized design is

proposed to improve supercapacitor reliability during high-_g_ impact. This paper reveals the fundamental nature of the high-_g_ impact failure of supercapacitors and has guiding

significance for avoiding the supercapacitor failure in practical applications. HIGH-_G_ RESPONSE MODEL OF SUPERCAPACITORS A supercapacitor or electrochemical capacitor is composed of two

electrodes, which are usually separated by an ion-permeable membrane, and an electrolyte ionically connecting both electrodes. It can be divided into two types: electrical double-layer

capacitors and pseudo capacitors. The regular double-layer capacitance results from the potential-dependence of the surface density of charges stored electrostatically at the interfaces of

the two electrodes. The pseudocapacitance results from Faradaic electron charge transfer with redox reactions, intercalation or electrosorption related to the electroactive materials. For

supercapacitors in practical applications, the double-layer capacitors usually exhibit perhaps 1–5% of their capacitance as pseudocapacitance owing to the Faradaic reactivity of surface

oxygen-functionalities. In contrast, pseudocapacitors usually exhibit 5–10% of their capacitance as electrostatic double-layer capacitance due to the ion adsorption/desorption in the

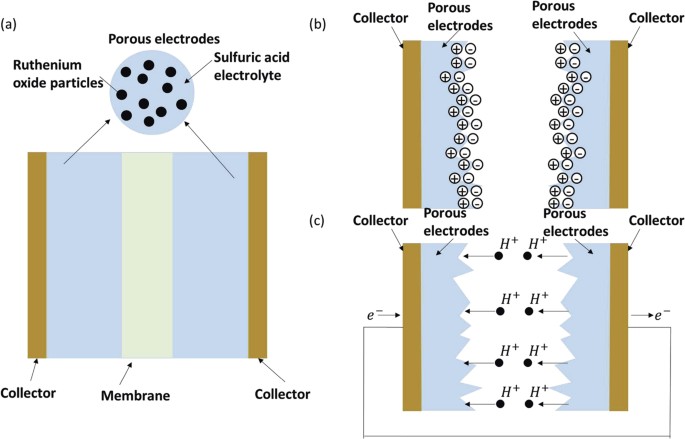
interfacial areas. With this in mind, we established a dynamic model based on a typical supercapacitor, which is schematically shown in Fig. 1(a). The porous electrodes are usually made of

materials with large surface areas, such as ruthenium oxide. A liquid electrolyte fully fills the pores of the electrodes and membrane. The energy storage mechanism of the supercapacitor is

based on a combination of the electrical double layer effect and the Faraday process. The electric double layer effect stores energy at the surface of the electrodes. As shown in Fig. 1(b),

the electrical double layer structure results from the electrical attraction between positive ions and negative ions. The Faraday process is a highly reversible redox reaction of the

electroactive species, and energy storage can be realized through the resulting electron transfer, as shown in Fig. 1(c). DYNAMIC MODEL FOR ENERGY STORAGE IN A SUPERCAPACITOR The energy

storage mechanism of a typical supercapacitor is shown in Fig. 1(b) and (c). Modeling and simulations are useful for theoretical research and optimizing designs of energy storage devices9.

For example, a dynamic modeling simulation is the most accurate and effective way to study the mechanism and characteristics of the charging and discharging processes10,11,12,13,14,15,16,17,

and it establishes a multi-faceted physics model composed of an electric field and an ion concentration field for the electrodes and the membrane, respectively. First, in the porous

electrode, the total current from the electrode phase to the electrolyte phase can be decomposed into the electric double layer current and the Faraday process current, where _i_l represents

the surface current density of the electrolyte phase, and _i_F and _i_DL represent the current density that result from the Faraday process and the electric double layer effect,

respectively. For the electrode phase, the relation between the current and the potential is given by Ohm’s law, where _i_s, _σ_s,eff and Φs represent the surface current density, the

effective conductivity and the potential of the electrode phase. For the porous materials, all effective parameters are derived from their material parameters using the Bruggeman method. For

example, , where _σ_s represents the electrical conductivity of ruthenium oxide and _ε_s represents the volume ratio of solid to total volume. However, for the electrolyte phase of the

electrode, Ohm’s law needs to be modified in light of the concentrated solution effect, where _i_l, _σ_l,eff and Φl represent the surface current density, the effective conductivity, and the

potential of the electrolyte phase of the electrode, respectively. _t_+ and _c_l are the transference number and ion concentration in the solution. _F, R_ and _T_ represent the Faraday

constant, Universal gas constant, and the temperature in Kelvin, respectively. The potential equation of the electrolyte phase can be obtained by combining equations (1) and (3), The

relation ∇ · _i_s + ∇ · _i_l = 0 must hold due to charge conservation. The potential equation of the electrode phase can then be obtained by combining this conservation equation with

equation (2), For the Faraday process, the binding and release of hydrogen ions at the surface of the ruthenium oxide is governed by classical porous electrode theory13. As shown in equation

(6), the ion concentration field is influenced by the current and the transfer of ions, where _ε_l and _D_l,eff represent the porosity of the electrode and the hydrogen ions diffusion

coefficient in the electrolyte, respectively. In the membrane, _i_s = 0 since it is an insulator. Thus, ∇ · _i_l = 0. One can write the potential equation for the electrolyte phase in the

membrane as, Similar to equation (6), the ion concentration equation for the electrolyte phase in the membrane can be obtained, since there is no Faraday current there. According to

electrochemical theory, the Faraday current can be calculated as: where _a_v represents the specific surface area of the electrodes and _j_loc represents the Faraday transfer current

density. The _a_v depends on porosity _ε_l, and the ruthenium oxide particle radius _r_p, The _j_loc term can be calculated by equation (10), according to the Butler-Volmer equation, where

_i_0 represents the Faraday exchange current density, _α_a and _α_c represent the transfer coefficients of the anode and cathode, and _U_oc is the open-circuit potential of the Faraday

process. The _U_oc for the positive and negative electrodes are both dependent on the extent of the redox reactions, where _θ_ represents the extent of the redox reactions, which can be

represented by the ratio between the hydrogen ion concentration _c_s of the electrode phase and the maximum achievable concentration _c_s,max, The _c_s,max depends on the microstructure of

ruthenium oxide, where _L_A represents Avogadro’s number and _h_ represents the lattice constant of ruthenium oxide. According to the theory proposed by Kim and Popov13, we can obtain the

conservation equations inside the ruthenium oxide particles (0 < _r_ < _r_p), The boundary condition for equation (15) is, The current density _i_DL created by the electric double

layer effect is, where _C_dl represents the capacitance associated with the electric double layer effect. Equations (1),(2),(3),(4),(5),(6),(7),

(8),(9),(10),(11),(12),(13),(14),(15),(16),(17) fully describe the mechanism of the supercapacitor’s charging and discharging processes, and constitute a dynamic model for energy storage in

the supercapacitor. A multi-faceted physics simulation for these processes can be realized by solving the model equations. DYNAMIC MODEL FOR SUPERCAPACITOR RESPONSE BASED ON THE FLUID AND

CONCENTRATION FIELDS To characterize the impact response of supercapacitors, the dynamic model for energy storage needs to be modified to account for the effects of a high-_g_ process. In

fact, an inhomogeneity in the hydrogen ion concentration always exists during the charging and discharging of the supercapacitor18, as shown in the left part of Fig. 2. The electrolyte will

flow under the influence of a high-_g_ impact, and this flow causes the hydrogen ions to redistribute homogeneously in a very short time, as shown in the right part of Fig. 2. The ion

distribution caused by a high-_g_ impact process has a significant influence on the performance of supercapacitors, which is discussed and modeled in the following section. The inhomogeneity

in the hydrogen ion concentration can be derived from a dynamic model proposed above. From equation (6) in the energy storage model of the supercapacitor, we can now consider the initial

state before the supercapacitor begins charging or discharging. At the beginning, there is no Faraday current in the supercapacitor, and the hydrogen ion concentration in the electrolyte is

homogeneous due to steady-state diffusion, As the supercapacitor begins to charge or discharge, there are opposite Faraday currents in the positive electrode and negative electrodes, and

hydrogen ions become bound to or released from these two electrodes. For the charging process, While for the discharging process, It can be concluded that the hydrogen ion concentrations of

the two electrodes change in an opposing manner. As a result, the homogeneity of the ion concentration no longer holds once the charging or discharging process begins, Fluid mechanics

dictates that the liquid will flow due to the effects of gravity or acceleration19, and electrochemistry predicts that the electric field of the system may be affected by the fluid nature of

the electrolyte20,21,22. The fluid field is controlled by the Navier-Stokes equations, where _u, ρ, p, μ_ and _a_ represent the flow velocity, the density of the liquid, the pressure of the

liquid, the dynamic viscosity, and the acceleration, respectively. The ion concentration in the electrolyte not only is influenced by the Faraday current and the diffusion effect but also

changes based on electrolyte flow. During an impact process, for example, a constant acceleration _a_ lasts for a period of time _t_g. Equation (6) cannot accurately describe the change of

ion concentration, and must be modified to include the fluid flow occurring during that time. For the electrodes, equation (6) should be modified as: For the membrane, After replacing

equations (6) and (8) with equations (24) and (25), a new model can be constructed with the electric field, ion concentration field, fluid field, and acceleration field. According to this

model, the primary mechanism of the impact response is the ion redistribution process shown in Fig. 2. During the discharging process of the supercapacitor, the hydrogen ion concentration is

larger at one electrode and smaller at the other due to ion release and binding during the Faraday process, as shown in the left part of Fig. 2. As the impact occurs, the electrolyte begins

to flow and causes the ions to redistribute homogeneously, as shown in the right part of Fig. 2. Thus, it can be concluded that acceleration can directly influence the fluid field of the

electrolyte and further change the ion concentration field and electric field of the supercapacitor, revealing the microscopic dynamic mechanism of the voltage fluctuations during high-_g_

impact. The details of the response are discussed in the following section using simulation results. An equivalent circuit diagram is also proposed to help understand the impact response

characteristics of supercapacitors intuitively. For a typical qualitative and semi-quantitative analysis of the charging and discharging process of a supercapacitor, the equivalent circuit

model in Fig. 3(a) is commonly used23,24,25. According to the equivalent circuit model shown in Fig. 3(a), the equivalent series capacitance _C_i0, _C_i1 and internal resistance _R_i

describe the fast transient response of the charging and discharging processes. In addition, the hysteresis loop composed of _C_d and _R_d characterizes the relaxation process of the

supercapacitor caused by the ion redistribution effect. For practical supercapacitors, the relaxation process is relatively slow and can be ignored during charging and discharging, which

means that the switch _k_1 between the hysteresis circuit and the main circuit will not close until the charging or discharging process is complete. According to the mechanism discussed in

equations (24) and (25), the impact process influences the supercapacitor through ion redistribution. The self-discharging theory of supercapacitors states that the relaxation process is

also caused by ion redistribution. Therefore, in order to take the supercapacitor’s response to acceleration into account, we should modify the typical equivalent circuit model, similar to

modeling the relaxation process, by adding another hysteresis circuit, as shown in Fig. 3(b). The impact response is modeled by the hysteresis circuit composed of _C_d and _R_s. This new

hysteresis circuit has a small response time, which means that and that the relaxation time constant _R_s_C_d is sufficiently small. When a high-_g_ impact happens, the switch _k_2 closes,

and this hysteresis circuit will be connected to the main circuit, resulting in a fast hysteresis process. The redistribution of charges between capacitors _C_d and _C_i0, _C_i1 will result

in a hysteresis current in the main circuit and fluctuate the output voltage _V_out. The simulations in this paper are based on the dynamic model proposed above because it analyzes the micro

scale impact response mechanism of the supercapacitor and is more accurate than the equivalent circuit model shown in Fig. 3(b). SIMULATION AND EXPERIMENT RESULTS Based on the dynamic model

for the impact response of the supercapacitor that takes into consideration the fluid field and the concentration field, a multi-faceted physics dynamic simulation is implemented. The

parameters in the simulations are shown in Table 1. Furthermore, to verify the validity of the dynamic model and the simulation, we tested the most important simulation conclusions

experimentally by the Machete hammer test, which can provide accelerations of up to 30000 _g_. The Machete hammer test is commonly used in high-_g_ impact experiments26 and can realize

high-_g_ impact by a violent collision process, with is caused by the huge kinetic energy of the counterweight, as shown in Fig. 4. We used a CHI 660 D electrochemical workstation to

establish a supercapacitor high-_g_ impact test platform. In the following part, we discuss the simulation and experimental results in detail. Two typical impact response processes are

simulated and their voltage responses are shown in Fig. 5(a) and (b). For case 1, the supercapacitor is charged with a large current, and the discharging process begins immediately after the

supercapacitor is fully charged. Then, the supercapacitor suffers high-_g_ impact. Figure 5(a) shows that the voltage of the supercapacitor fluctuates downward when the impact occurs under

this condition; in other words, Δ_V_ < 0, where Δ_V_ represents the voltage increase during the impact process. For case 2, the supercapacitor begins to discharge after a long

self-discharging process, and the high-_g_ impact occurs during the discharging process. Figure 5(b) shows that the voltage of the supercapacitor fluctuates upward (Δ_V_ > 0) when impact

occurs in this condition, in contrast to case 1 in Fig. 5(a). The experimental results also verify the two opposite voltage fluctuations for case 1 and case 2. Corresponding to case 1 in the

simulation, the supercapacitor is first charged with a 20 mA current. The discharging process begins immediately after the supercapacitor is fully charged, and the high-_g_ impact occurs

shortly after the discharge begins. The experimental results clearly show the voltage drop (Δ_V_ < 0) in Fig. 5(c). Corresponding to case 2 of the simulation, the supercapacitor is

maintained at a constant voltage for a long time after it is fully charged. After the long period of constant voltage, the supercapacitor begins to discharge with a 20 mA current. The

experimental results clearly show the voltage increase (Δ_V_ > 0) in Fig. 5(d). The experimental phenomena shown in Fig. 5(c) and (d) are highly consistent with the simulation phenomenon

shown in Fig. 5(a) and (b) and verify the validity of the proposed model. To understand the nature of the two different failure phenomenon shown in Fig. 5, it is necessary to further study

the changes of hydrogen ion concentration distribution in the electrolyte during the impact process. It is difficult to measure the ion concentration distribution experimentally during the

impact process because the distribution changes dramatically during a short process and the ion concentration measurements are challenging to implement under such extreme conditions. Thus,

we calculated the ion concentration distribution by simulation based on the proposed model. For case 1, while charging with a large current, the Faraday reaction releases hydrogen ions much

faster than the rate of ion diffusion in the electrolyte. As a result, a large number of hydrogen ions are released and accumulated on the positive electrode, while hydrogen ions on the

negative electrode are consumed at the same time. Before the high-_g_ impact occurs, the hydrogen ion concentration at the positive electrode is much greater than at the negative electrode,

as shown by the black line in Fig. 6(a). After the impact begins, the electrolyte flow quickly changes the distribution of the hydrogen ions in the electrolyte, and the ion concentration

returns to a homogeneous state in a short time. This process is shown in Fig. 6(a), where _t_s represents the time from the beginning of the impact. According to equation (5), the ion

concentration _c_l directly influences the electrolyte potential Φl, which impacts the output voltage of supercapacitor. This voltage fluctuation can be attributed to the electrolyte ions

redistribution effect18. During the discharging process of the supercapacitor, hydrogen ions are bound to the positive electrode. The impact process makes the hydrogen ion concentration more

homogeneous and reduces the hydrogen ion concentration at the positive electrode. The decrease of hydrogen ions at the positive electrode reduces the discharging capacity of the

supercapacitor and makes the output voltage drop. In contrast, the ion concentration distribution of case 2, as shown in Fig. 6(b), has already become homogeneous after a long

self-discharging process, according to the self-discharging theory of supercapacitors18. Then, as the supercapacitor discharges with a large current, the ion concentration at the negative

electrode significantly exceeds that of the positive electrode, as shown by the black line in Fig. 6(b). During the impact process, the ion concentration becomes homogeneous in a short time.

According to equation (5), the influence of the ion concentration _c_l on the electric field depends on the value of ∇ln(_c_l). Due to the opposite values of ∇ln(_c_l) in Fig. 6(a) and (b),

the voltage fluctuations in case 2 are opposite to that in case 1. As shown in Fig. 5(b), there is an upward voltage fluctuation, rather than a downward one, during the impact process.

Based on the electrolyte ion redistribution, the electrolyte flow resulting from a high-_g_ impact makes the hydrogen ion concentration more homogeneous and increases the hydrogen ion

concentration at the positive electrode. As the electrolyte provides more hydrogen ions for the Faraday process, the discharge capacity is improved, and the output voltage increases. To

summarize, the voltage fluctuation is determined by the ion concentration distribution at the time of the impact. If the hydrogen ions are concentrated at the positive electrode at the

initial time (_c_l|positive > _c_l|negative), the voltage fluctuates downward (Δ_V_ < 0) during the impact process, as shown in the Figs 5(a) and 6(a). Conversely, as shown in Figs

5(b) and 6(b), when the hydrogen ions are concentrated at the negative electrode at the initial time (_c_l|positive < _c_l|negative), the voltage fluctuates upward (Δ_V_ > 0) during

the impact process. The analysis above demonstrates that the voltage fluctuation generated by the impact process depends on the hydrogen ion concentration of the electrolyte. Further

simulation results will elaborate on this conclusion in detail. Considering the supercapacitors used in practical applications, most of them will not begin to discharge until they are fully

self-discharged. For this reason, the following simulation will focus on the case 2 discussed above. Figure 7(a) shows the voltage fluctuations with different discharging currents and

different discharging levels when the high-_g_ impacts occur. We define the discharging level as the ratio of the output voltage when the high-_g_ impact occurs to the maximum voltage when

the supercapacitor is fully charged. The results in Fig. 7(a) show the character of the impact response. First, for the same discharging current, as the discharging level increases, the

voltage fluctuation becomes larger. Second, for a larger discharging current, the voltage increase is larger. Third, for relatively small discharging currents, when the discharging level is

low, the voltage increase is approximately a linear function of the discharging level. However, as the discharging level continues to increase and approaches 1, the amplitude of voltage

fluctuation increases relatively slowly and finally approaches a constant value. Corresponding to the simulation results in Fig. 7(a), the amplitudes of voltage fluctuation under different

discharge currents and discharging levels are experimentally measured. The experimental results in Fig. 7(b) show that the amplitude of voltage fluctuation increases as the discharging level

and discharging current increase. According to the experimental results in Fig. 7(b), when the discharging current is small, as the discharging level increases, the amplitude of the voltage

fluctuation increases slower and slower, similar to the convergence phenomenon illustrated by the black line of Fig. 7(a). The only difference between the simulation and experimental

results is that the experimentally measured voltage fluctuation amplitudes are always larger than the simulated ones under certain discharging current and discharging levels. This phenomenon

is due to the piezoresistive effect of the supercapacitor electrodes. The porous electrode is piezoresistive and has less resistance during the high-_g_ impact due to the huge pressure. The

decrease of the electrode resistance reduces the voltage of the electrode. As a result, the output voltage of the supercapacitor will increase. This output voltage increase caused by the

piezoresistive effect of the electrode accounts for the difference between the simulated and experimentally measured voltage fluctuation amplitudes. The qualitative consistency between the

simulation (Fig. 7(a)) and experiment (Fig. 7(b)) further proves the validity of the proposed model. These important findings from simulations and experiments can be explained by the ion

concentration simulations in Fig. 7(c) and (d). First, the concentration difference results from the accumulation of Faraday current. Thus, as the discharging level increases, more ions

accumulate at the negative electrode, and the concentration difference becomes larger. As a result, homogenization of the concentration field caused by the high-_g_ impact process will

influence the electric field more significantly. Second, a concentration difference arises from the fact that the ion release rate in the Faraday reaction exceeds the diffusion rate. As the

discharging current becomes larger, the Faraday reaction becomes more dramatic, and the concentration difference becomes larger. Third, according to equation (18), the rate of diffusion

depends on the concentration difference. As the concentration difference becomes sufficiently large, the diffusion effect can offset the ion release in the Faraday reaction and keep the

concentration stable, as shown in Fig. 7(c). Thus, the voltage fluctuation approaches a constant value, although the discharging level continues to increase. The simulation and experimental

results both show that supercapacitors suffer voltage fluctuations during high-_g_ impact processes. The inhomogeneity of the ion concentration and the electrolyte flow are the two primary

reasons for these voltage fluctuations. To avoid this failure during high-_g_ impact, it is necessary to reduce the inhomogeneity of ion concentration or the electrolyte flow, which can be

achieved by using a large diffusion-coefficient electrolyte and a solid electrolyte, respectively. To reduce the inhomogeneity of the ion concentration, it is worthwhile to use an

electrolyte with a large diffusion coefficient. According to equations (24) and (25), such an electrolyte will allow ions to diffuse more quickly and reduce the ion inhomogeneity, resulting

in a smaller effect by a high-_g_ impact. It is also helpful to use a solid electrolyte, which does not flow when the impact occurs, unlike a liquid one, so that the ion concentration and

output voltage can remain stable during a short duration impact process. CONCLUSIONS This paper investigates the failure of a supercapacitor during a high-_g_ impact. The impact response

mechanism of the supercapacitor is analyzed, and a dynamic model for the voltage response is established. Based on this model, a multi-faceted physics simulation of the supercapacitor under

a high-_g_ impact is achieved, and the experimental results verify the proposed model and simulation. According to this model, the high-_g_ impact causes the electrolyte to flow and results

in a change of ion concentration distribution, which further influences the electric field and makes the supercapacitor’s voltage fluctuate. Simulation results indicate that the

inhomogeneity of ion concentration and the electrolyte flow are the two primary factors that control these voltage fluctuations. There will be larger fluctuations when there is a larger

inhomogeneity of the ion concentration. To avoid this failure during high-_g_ impacts, it is suggested that electrolytes with a large diffusion coefficient or a solid electrolyte be used for

supercapacitors. ADDITIONAL INFORMATION HOW TO CITE THIS ARTICLE: Dai, K. _et al_. Voltage Fluctuation in a Supercapacitor During a High-_g_ Impact. _Sci. Rep._ 6, 38794; doi:

10.1038/srep38794 (2016). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES * Yuan, Z.,

Zhang, Y., Fu, W., Li, Z. & Liu, X. Investigation of a small-volume direct methanol fuel cell stack for portable applications. Energy 51, 462–467 (2013). Article  CAS  Google Scholar  *

Yi, F. et al. Stretchable-rubber-based triboelectric nanogenerator and its application as self-powered body motion sensors. Advanced Functional Materials 25, 3688–3696 (2015). Article  CAS

  Google Scholar  * Wang, X., Yin, Y., Hao, C. & You, Z. A high-performance three-dimensional micro supercapacitor based on ripple-like ruthenium oxide-ccarbon nanotube composite films.

Carbon 82, 436–445 (2015). Article  CAS  Google Scholar  * Wang, X.-f., Ruan, D.-b. & You, Z. Application of spherical ni(oh)(2)/cnts composite electrode in fp asymmetric supercapacitor.

Transactions Of Nonferrous Metals Society Of China 16, 1129–1134 (2006). Article  CAS  Google Scholar  * Wang, X., Yin, Y., Li, X. & You, Z. Fabrication of a symmetric micro

supercapacitor based on tubular ruthenium oxide on silicon 3d microstructures. Journal of Power Sources 252, 64–72 (2014). Article  ADS  Google Scholar  * Yu, L., Zhang, G., Yuan, C. &

Lou, X. W. Hierarchical nico2o4@mno2 core-shell heterostructured nanowire arrays on ni foam as high-performance supercapacitor electrodes. Chemical Communications 49, 137–139 (2013). Article

  CAS  Google Scholar  * Chen, H., Hu, L., Chen, M., Yan, Y. & Wu, L. Nickel-cobalt layered double hydroxide nanosheets for high-performance supercapacitor electrode materials. Advanced

Functional Materials 24, 934–942 (2014). Article  Google Scholar  * Jing, P. _High-g impact test value of the research of key technologies_. Master’s thesis, North University of China

(2009). * Niu, S. et al. Theoretical study of contact-mode triboelectric nanogenerators as an effective power source. Energy & Environmental Science 6, 3576–3583 (2013). Article  Google

Scholar  * Lin, C., Ritter, J. A., Popov, B. N. & White, R. E. A mathematical model of an electrochemical capacitor with double-layer and faradaic processes. Journal of the

Electrochemical Society 146, 3168–3175 (1999). Article  CAS  Google Scholar  * Farsi, H. & Gobal, F. A mathematical model of nanoparticulate mixed oxide pseudocapacitors; part i: model

description and particle size effects. Journal Of Solid State Electrochemistry 13, 433–443 (2009). Article  CAS  Google Scholar  * Farsi, H. & Gobal, F. A mathematical model of

nanoparticulate mixed oxide pseudocapacitors; part ii: the effects of intrinsic factors. Journal Of Solid State Electrochemistry 15, 115–123 (2011). Article  CAS  Google Scholar  * Kim, H.

& Popov, B. N. A mathematical model of oxide/carbon composite electrode for supercapacitors. Journal of the Electrochemical Society 150, A1153–A1160 (2003). Article  CAS  Google Scholar

  * Johnson, A. M. & Newman, J. Desalting by means of porous carbon electrodes. Journal of the Electrochemical Society 118, 510–517 (1971). Article  CAS  Google Scholar  * Srinivasan, V.

& Weidner, J. W. Mathematical modeling of electrochemical capacitors. Journal of the Electrochemical Society 146, 1650–1658 (1999). Article  CAS  Google Scholar  * Lin, C., Popov, B. N.

& Ploehn, H. J. Modeling the effects of electrode composition and pore structure on the performance of electrochemical capacitors. Journal of the Electrochemical Society 149, A167–A175

(2002). Article  CAS  Google Scholar  * Farsi, H. & Gobal, F. Theoretical analysis of the performance of a model supercapacitor consisting of metal oxide nano-particles. Journal of Solid

State Electrochemistry 11, 1085–1092 (2007). Article  CAS  Google Scholar  * Hao, C., Wang, X., Yin, Y. & You, Z. Analysis of charge redistribution during self-discharge of double-layer

supercapacitors. Journal of Electronic Materials 45, 2160–2171 (2016). Article  CAS  ADS  Google Scholar  * Evett, J. B. & Liu, C. Fundamentals of fluid mechanics (McGraw-Hill College,

New York, 1987). * Chen, D., Li, G., Wang, J., Chen, J. & He, W. A micro electrochemical seismic sensor based on mems technologies. Sensors and Actuators A: Physical 202, 85–89 (2013).

Article  CAS  Google Scholar  * Deng, T., Chen, D., Wang, J., Chen, J. & He, W. A mems based electrochemical vibration sensor for seismic motion monitoring. Journal of

Microelectromechanical Systems 23, 92–99 (2014). Article  Google Scholar  * Sun, Z. & Agafonov, V. M. 3d numerical simulation of the pressure-driven flow in a four-electrode rectangular

micro-electrochemical accelerometer. Sensors and Actuators B: Chemical 146, 231–238 (2010). Article  CAS  Google Scholar  * He, Y., You, Z. & Wang, X. Modelling of a hybrid energy system

for autonomous application regular paper. International Journal of Advanced Robotic Systems 10, 356 (2013). Article  Google Scholar  * Yang, H. & Zhang, Y. Evaluation of supercapacitor

models for wireless sensor network applications. In _Signal Processing and Communication Systems (ICSPCS_)_, 2011 5th International Conference on_, 1–6 (IEEE, 2011). * Zubieta, L. &

Bonert, R. Characterization of double-layer capacitors for power electronics applications. IEEE Transactions on Industry Applications 36, 199–205 (2000). Article  Google Scholar  * Li, Y.,

Chen, J. & Wang, Y. The study on anti-high-g technology of missile body attitude measurement system. In _Automatic Control and Artificial Intelligence (ACAI 2012_)_, International

Conference on_, 2195–2198 (IET, 2012). Download references AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Department of Precision Instrument, Collaborative Innovation Center for Micro/Nano

Fabrication, Device and System, State Key Laboratory of Precision Measurement Technology and Instruments, Tsinghua University, Beijing, 100084, China Keren Dai, Xiaofeng Wang, Yajiang Yin, 

Chenglong Hao & Zheng You Authors * Keren Dai View author publications You can also search for this author inPubMed Google Scholar * Xiaofeng Wang View author publications You can also

search for this author inPubMed Google Scholar * Yajiang Yin View author publications You can also search for this author inPubMed Google Scholar * Chenglong Hao View author publications You

can also search for this author inPubMed Google Scholar * Zheng You View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Keren Dai proposed the

multi-field coupled kinetics model, Keren Dai and Chenglong Hao conceived the simulation, Keren Dai and Xiaofeng Wang conceived the experiments, Keren Dai and Yajiang Yin conducted the

experiments, Keren Dai and Zheng You analysed the results. All authors reviewed the manuscript. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing financial interests.

RIGHTS AND PERMISSIONS This work is licensed under a Creative Commons Attribution 4.0 International License. The images or other third party material in this article are included in the

article’s Creative Commons license, unless indicated otherwise in the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission

from the license holder to reproduce the material. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Dai, K., Wang, X., Yin, Y. _et al._ Voltage Fluctuation in a Supercapacitor During a High-_g_ Impact. _Sci Rep_ 6, 38794 (2016). https://doi.org/10.1038/srep38794 Download citation *

Received: 13 September 2016 * Accepted: 14 November 2016 * Published: 13 December 2016 * DOI: https://doi.org/10.1038/srep38794 SHARE THIS ARTICLE Anyone you share the following link with

will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative