Reader TTS

ABSTRACT Hopping-type charge transport in an amorphous thin layer composed of organic molecules is simulated by the combined use of molecular dynamics, quantum chemical, and Monte Carlo

calculations. By explicitly considering the molecular structure and the disordered intermolecular packing, we reasonably reproduce the experimental hole and electron mobilities and their

applied electric field dependence (Poole–Frenkel behaviour) without using any adjustable parameters. We find that the distribution of the density-of-states originating from the amorphous

nature has a significant impact on both the mobilities and Poole–Frenkel behaviour. Detailed analysis is also provided to reveal the molecular-level origin of the charge transport, including

the origin of Poole–Frenkel behaviour. SIMILAR CONTENT BEING VIEWED BY OTHERS ELUCIDATION OF MOLECULAR-LEVEL CHARGE TRANSPORT IN AN ORGANIC AMORPHOUS SYSTEM Article Open access 18 February

2025 TRANSIENTLY DELOCALIZED STATES ENHANCE HOLE MOBILITY IN ORGANIC MOLECULAR SEMICONDUCTORS Article 14 September 2023 INTERMEDIATE POLARONIC CHARGE TRANSPORT IN ORGANIC CRYSTALS FROM A

MANY-BODY FIRST-PRINCIPLES APPROACH Article Open access 11 April 2022 INTRODUCTION Charge mobility _μ_ in organic aggregates is a key factor in understanding the device performance of

organic semiconductor devices such as organic light-emitting diodes (OLEDs)1,2,3. Typical organic layers of OLEDs are composed of amorphous thin films. Charge transport in amorphous organic

solids is considered to occur through intermolecular charge hopping. Some models have been proposed to describe charge transport in amorphous organic solids. Among these models, the Gaussian

disorder model4 successfully describes the macroscopic charge transport property. However, the model does not consider actual molecules and it has difficulty in revealing the molecular

scale behaviour of carriers; the disorders, which originate from amorphous structures, are used as adjustable parameters to reproduce the experimental mobility data. Although microscopic

analyses have also been carried out5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23 and some useful suggestions have been derived, we only have a limited understanding of the nature of

charge transport in amorphous organic layers. In these studies, Marcus theory24 have frequently been employed to calculate rate constants _k__ij_ of intermolecular charge transfer between

molecule _i_ and molecule _j_, described as: Here, _H__ij_ is the electronic coupling between molecule _i_ and _j_. Δ_G__ij_ is the difference of Gibbs free energy between the initial and

final states associated with the charge transfer from molecule _i_ to _j. λ_ is the reorganization energy, _h_ is Planck constant, _k_B is Boltzmann constant, and _T_ is the absolute

temperature. Our goals are to build a computational model reproducing the experimental _μ_ quantitatively, and to gain understanding of the nature of charge transport in amorphous organic

layers by analysing the model. We have recently carried out simulations in an amorphous organic solid23. The calculated _μ_ was overestimated by two orders of magnitude, which also failed to

reproduce the experimental observation that _μ_ increased as the applied electric field _F_ increased. Here, charge transport process in an amorphous solid of

4,4′-bis(_N_-carbazolyl)-1,1′-biphenyl (CBP) (Supplementary Fig. S1), which is a typical host material for OLEDs, was investigated. In the calculations, we considered the energetic disorder

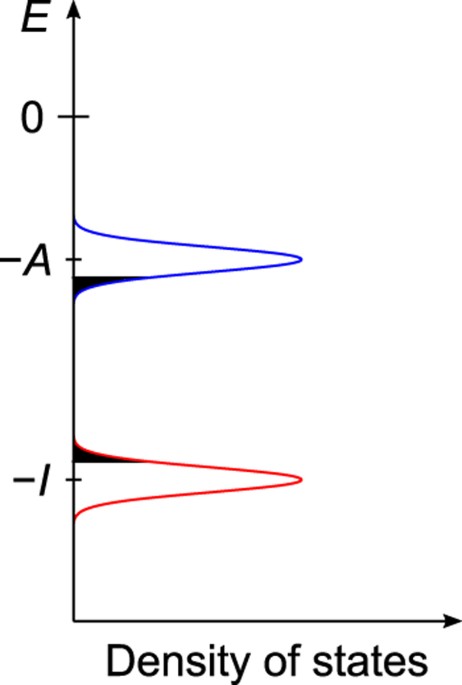
(Fig. 1, see below for details) and intermolecular packing effect on _λ_, both of which were not included in a preceding paper23. An amorphous structure containing 4000 CBP molecules was

generated using a molecular dynamics (MD) simulation. On the basis of the amorphous structure, _H__ij_ and _λ_ were calculated by quantum chemical calculations. Reflecting the amorphous

nature, the calculated _H__ij_ values were distributed as shown in Supplementary Figs S2 and S3. The “structural disorder” is often called the “off-diagonal disorder”. In the Gaussian

disorder model4, material points on a cubic lattice are considered instead of real molecules, and the structural disorder is only an adjustable parameter to describe the experimental

results. Here, real molecules are considered; not only the distribution of distances, but also the relative intermolecular orientation and the distribution of frontier orbitals contribute to

the distribution of _H__ij_. Examples of the intermolecular packing generated by the above-mentioned MD simulation are shown in Supplementary Fig. S4. From the examples and an

intermolecular distance dependence of _H__ij_ (Supplementary Fig. S2), we find that _H__ij_ values are not solely determined by the intermolecular distances. In addition to the structural

disorder, molecules (hopping sites) are distributed in energy in amorphous solids (Fig. 1), because different molecules undergo a different intermolecular interaction. The distribution of

energy is called the “energetic disorder” or “diagonal disorder”. We calculated the energetic disorder by considering distributed electrostatic interaction with and polarization effect of

neighbouring molecules. The energy of a hole/electron on molecule _i_, , can be written as: Here, _I_isolated and _A_isolated are the ionization potential and electron affinity of an

isolated CBP molecule, respectively. , , and are the sum of electrostatic interaction with and polarization effect of neighbouring molecules, for positively charged, negatively charged, and

the neutral state of molecule _i_, respectively. Therefore, Δ_G__ij_ can be expressed as: where Δ_E__k_ (_k_ = _i,j_) is or for hole or electron transport, _q_ is the charge of the carrier,

_F_ is an externally applied electric field (|_F_| = _F_) and _X__ij_ is a vector connecting the centre of molecule _i_ to the centre of molecule _j_ (displacement of the carrier). The

calculations in this study show that the distribution of the energy level was Gaussian (see Supplementary Fig. S5) and its sample standard deviation was 0.107 and 0.102 eV for the hole and

electron, respectively. _λ_ was calculated taking into account the steric influence of neighbouring molecules with the quantum mechanics / molecular mechanics method. Using the calculated

_H__ij_, Δ_G__ij_, and _λ, k__ij_ were calculated from equation (1). The charge transport process was simulated using kinetic Monte Carlo method based on the MD-constructed amorphous

structure and the _k__ij_, which provided the calculated _μ_ (examples of calculated trajectories are shown in Supplementary Fig. S6). To confirm the validity of the calculations, we also

performed time-of-flight (TOF) experiments. The experimental data were consistent with those reported previously20,25,26. More details of the computational and the experimental methods are

shown later and and in the Supplementary Information. Figure 2 compares the experimentally-obtained and the calculated _μ_ for the hole and electron transport. The experimental _μ_ (black

filled and black open symbols in Fig. 2) shows a positive linear _F_1/2-dependence, often called Poole–Frenkel (PF)-type behaviour, commonly observed in organic amorphous materials1,4,27.

Open circles in Fig. 2 consider the intermolecular packing effect in the calculations of _λ_ but the energetic disorder is not considered. Here, the _λ_ including the intermolecular packing

effect in amorphous aggregates is denoted by _λ_aggr. The calculated _μ_ significantly deviate from the experimental values, being one or two orders of magnitude larger. In addition, the

calculated negative _F_1/2-dependence is not compatible with the experiments. Open squares in Fig. 2 show the calculated _μ_ incorporating the energetic disorder but the intermolecular

packing effect on _λ_ is not considered (calculated reorganization energy is noted as _λ_isolated). By considering the energetic disorder, the experimentally-obtained positive

_F_1/2-dependence is reproduced. The _μ_ is more than one order of magnitude smaller compared with the experiments for electron transport. By incorporating both the energetic disorder and

the intermolecular packing effect on _λ_, we obtain the filled squares in Fig. 2. The calculated _μ_ showed a better agreement with the experimentally-obtained values. A slightly worse

agreement for electron transport is proposed to reflect the difficulty in calculating unoccupied orbitals. We investigate the origin of the PF behaviour, the positive _F_1/2-dependence of

_μ_. Figure 2 shows that the PF behaviour is reproduced when the energetic disorder is incorporated in the simulations, but not reproduced when the energetic disorder is not incorporated.

Therefore, the energetic disorder plays a crucial role in the PF behaviour. To investigate the mechanism of influence of the energetic disorder on the _F_1/2-dependence of _μ_, we calculated

the number of hops during the transport _n_, the number of hopping sites used at least once during the transport _ν_, and the mean time required for each individual charge hopping _τ_ = 

_t_/_n (t_ is the time required for the charge transport between electrodes), with and without the energetic disorder (see Table 1. The intermolecular packing effect on _λ_ is considered in

all cases.). When the energetic disorder is included in the simulations, _n_ decreases by two orders of magnitude with _F_1/2 increasing from 300 V1/2cm−1/2 to 1300 V1/2cm−1/2, while _τ_ has

the same order of magnitude regardless of _F_. Since _μ_ = _L_/(_tF_) = _L_/(_nτF_), the PF behaviour is mainly attributed to the decrease in _n_ with _F_. Here, _L_ is the distance between

the electrodes. When _F_1/2 = 300 V1/2cm−1/2 and under the existence of the energetic disorder, _n_ is larger than _ν_ by two orders of magnitude, indicating that the same sites are

repeatedly used. Hence, the charge carriers frequently move back and forth during the charge transport. This “round-trip” of carriers is enhanced by the energetic disorder: without the

energetic disorder, _n_ has the same order as or is one order of magnitude larger than that of _ν_. Different from the case of _F_1/2 = 300 V1/2cm−1/2, the differences of _n_ and _ν_ are

much smaller when _F_1/2 = 1300 V1/2cm−1/2, regardless of whether the energetic disorder is incorporated or not. In summary, the energetic disorder causes frequent back and forth hopping of

carriers and entails large _n_ under weak _F_, but not under strong _F_. This results in the PF behaviour. When we compare the simulations with and without the energetic disorder under the

same _F_1/2, not only _n_ but also _τ_ become larger by incorporation of the energetic disorder. Both factors affect the reduced _μ_ for the case with energetic disorder. When we compare

hole and electron transport with the same _F_1/2 and energetic disordered state, _n_ and _ν_ are not significantly different but _τ_ is one to two orders of magnitude larger for electron

transport. The larger _τ_ induces a smaller _μ_ for electrons in spite of the maximum _H__ij_ for electron transports (70 meV) being larger than that of hole transports (41 meV). This

implies that _μ_ is not solely determined by the largest _H__ij_. These characteristics can be explained at the molecular level. Figure 3 shows the number of hops into site _i_ (here, we

call it ) versus their site energies . When _F_1/2 = 300 V1/2cm−1/2, is nearly exponential with the site energies, indicating that the charges mainly use “low-energy” sites (black filled

area in Fig. 1) during the transport, that is, charge carriers tend to jump into “low-energy” hopping sites. Here, we note that the “low-energy” site for hole (electron) has a positively

(negatively) high energy for the hopping site, as shown in Fig. 1. When the charge carriers escape from the low-energy hopping sites, they tend to back into the low-energy sites owing to the

difference of the site energies. Hence, the charge carriers frequently move forward and backward between the low-energy sites and the neighbouring sites under _F_1/2 = 300 V1/2cm−1/2. The

small number of low-energy sites significantly decreases _μ_ under weak _F_ as demonstrated in the following manner. Figure 4 shows _μ_ versus _F_1/2 with low-energy 1%, 3%, and 5% of all

sites removed. From Fig. 4, _μ_ is found to be significantly influenced by the small number (1–5%) of low-energy sites when _F_1/2 = 300 V1/2cm−1/2: it is often considered that low-energy

sites trap carriers. Our results suggest that carriers hop back and forth between low-energy sites and the neighbouring sites. The carriers are not frozen in the low-energy sites, but the

“round-trip” of carriers consequently consumes much time; therefore, this may also be comprehended as a kind of “trap”. On the contrary, when _F_1/2 = 1300 V1/2cm−1/2, the correlation

between and the site energy is weak [Fig. 3(c)]. Figure 4 clearly shows that _μ_ does not change irrespective of the existence of low-energy sites at _F_1/2 = 1300 V1/2cm−1/2, indicating

that these sites do not work as “traps”. Charge carriers tend to move along with _F_ regardless of the energetic disorder. Next, we discuss the influence of _H__ij_ distribution on _μ.

H__ij_ was distributed over the range of 0 to 41 meV and 0 to 70 meV for the hole and electron, respectively (Supplementary Fig. S3). The kinetic Monte Carlo simulations were also performed

without molecular pairs with _H__ij_ <  0.1, 1.0, 2.0 and 3.0 meV, and the calculated _μ_ are shown in Fig. 5. The molecular pairs with _H__ij_ < 0.1 meV do not affect the charge

transports (open circles in Fig. 5 are overlapped with filled squares). However, the contributions of the pairs with _H__ij_ <  1.0, 2.0 and 3.0 meV are significant, especially at strong

_F_. When the pairs with _H__ij_ < 3.0 meV are removed (downward open triangles in Fig. 5), _μ_ decreases by three or four orders of magnitude. This result clearly shows that the pairs

with _H__ij_ < 3.0 meV are frequently used as charge hopping sites although the _H__ij_ values are much smaller than the maximum _H__ij_ (41 meV and 70 meV for hole and electron hopping,

respectively). Hence, the decrease in _μ_ by removing pairs with _H__ij_ < 1.0–3.0 meV is attributed to the change in charge transport paths. This result indicates that in amorphous

aggregates, weakly coupled pairs significantly contribute to _μ_ by forming effective charge transport paths especially at strong _F_. From the above discussion, in amorphous thin layers,

_μ_ is not simply determined by the maximum _H__ij_ and therefore the maximum _k__ij_, although the values of _μ_ are often discussed by the _H__ij_ or _k__ij_. This feature is different

from that of crystalline solids. Thus, consideration of different hierarchical structures is crucial for the understanding of _μ_ in amorphous organic aggregates. In conclusion, _μ_ was

quantitatively reproduced without any adjustable parameters, by taking into account both the disorder of the energy level of the hopping sites and the disordered structure. The PF behaviour

was also reproduced, and its origin was attributed to the influence of the energetic disorder on the charge transport trajectory: under weak _F_, charge carriers go back and forth owing to

the difference of the site energies; however, under strong _F_, charge carriers tend to move simply along _F_. In amorphous organic solids, molecular pairs with relatively small _H__ij_ are

found to largely contribute to _μ_, indicating that they form effective paths for charge transport. METHODS SIMULATION OF CHARGE TRANSPORT PROCESS Simulations of the charge transport process

for amorphous structure containing 100, 1000, 4000, and 8000 molecules of CBP were performed. The results for the 4000 CBP system are provided in the main text. The MD simulation was

performed on LAMMPS program package28. Density functional theory and extended Hückel calculations were carried out using the Gaussian 09 program package29. Kinetic Monte Carlo simulations

were performed using our in-house program. Details of methodology are described in Supplementary Information. EXPERIMENTAL TOF MEASUREMENT _μ_ was experimentally measured for a CBP thin film

using TOF apparatus (TOF-401-3, Sumitomo Heavy Industries Advanced Machinery Co., Ltd., Japan). A TOF sample with the structure of ITO (50 nm)/CBP (3.9 μm)/Al (20 nm) was fabricated by

vacuum-deposition. A N2 gas laser (KEC-150, Usho Optical Systems Co., Ltd., Japan) with a wavelength of 337 nm was used to generate the photocarriers. ADDITIONAL INFORMATION HOW TO CITE THIS

ARTICLE: Uratani, H. _et al_. Detailed analysis of charge transport in amorphous organic thin layer by multiscale simulation without any adjustable parameters. _Sci. Rep._ 6, 39128; doi:

10.1038/srep39128 (2016). PUBLISHER'S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. REFERENCES *

Coropceanu, V. et al. Charge transport in organic semiconductors. Chem. Rev. 107, 926–952 (2007). Article  CAS  Google Scholar  * Tang, C. W. & VanSlyke, S. A. Organic electroluminescent

diodes. Appl. Phys. Lett. 51, 913–915 (1987). Article  CAS  ADS  Google Scholar  * Adachi, C., Tsutsui, T. & Saito, S. Organic electroluminescent device having a hole conductor as an

emitting layer. Appl. Phys. Lett. 55, 1489–1491 (1989). Article  CAS  ADS  Google Scholar  * Bässler, H. Charge transport in disordered organic photoconductors a Monte Carlo simulation

study. Phys. Status Solidi B 175, 15–56 (1993). Article  ADS  Google Scholar  * Cornil, J., Beljonne, D., Calbert, J. P. & Brédas, J.-L. Interchain interactions in organic _π_-conjugated

materials: Impact on electronic structure, optical response, and charge transport. Adv. Mater. 13, 1053–1067 (2001). Article  CAS  Google Scholar  * Brédas, J.-L., Calbert, J. P., da Silva

Filho, D. A. & Cornil, J. Organic semiconductors: A theoretical characterization of the basic parameters governing charge transport. Proc. Natl. Acad. Sci. USA 99, 5804–5809 (2002).

Article  ADS  Google Scholar  * Lin, B. C., Cheng, C. P., You, Z.-Q. & Hsu, C.-P. Charge transport properties of tris(8-hydroxyquinolinato)aluminum(III): Why it is an electron

transporter. J. Am. Chem. Soc. 127, 66–67 (2005). Article  CAS  Google Scholar  * Hutchison, G. R., Ratner, M. A. & Marks, T. J. Intermolecular charge transfer between heterocyclic

oligomers. Effects of heteroatom and molecular packing on hopping transport in organic semiconductors. J. Am. Chem. Soc. 127, 16866–16881 (2005). Article  CAS  Google Scholar  * Kirkpatrick,

J. & Nelson, J. Theoretical study of the transfer integral and density of states in spiro-linked triphenylamine derivatives. J. Chem. Phys. 123, 084703 (2005). Article  ADS  Google

Scholar  * Li, H., Brédas, J.-L. & Lennartz, C. First-principles theoretical investigation of the electronic couplings in single crystals of phenanthroline-based organic semiconductors.

J. Chem. Phys. 126, 164704 (2007). Article  ADS  Google Scholar  * Datta, A., Mohakud, S. & Pati, S. K. Electron and hole mobilities in polymorphs of benzene and naphthalene: Role of

intermolecular interactions. J. Chem. Phys. 126, 144710 (2007). Article  ADS  Google Scholar  * Kwiatkowski, J. J. et al. Simulating charge transport in tris(8-hydroxyquinoline) aluminium

(Alq3). Phys. Chem. Chem. Phys. 10, 1852–1858 (2008). Article  CAS  Google Scholar  * Nagata, Y. & Lennartz, C. Atomistic simulation on charge mobility of amorphous

tris(8-hydroxyquinoline) aluminum (Alq3): Origin of Poole–Frenkel–type behavior. J. Chem. Phys. 129, 034709 (2008). Article  ADS  Google Scholar  * Lukyanov, A., Lennartz, C. &

Andrienko, D. Amorphous films of tris(8-hydroxyquinolinato)aluminium: Force-field, morphology, and charge transport. Phys. Status Solidi A 206, 2737–2742 (2009). CAS  Google Scholar  *

Yamada, T., Sato, T., Tanaka, K. & Kaji, H. Percolation paths for charge transports in N,N′-diphenyl-N,N′-di(m-tolyl)benzidine (TPD). Org. Electron. 11, 255–265 (2010). Article  CAS 

Google Scholar  * Difley, S., Wang, L.-P., Yeganeh, S., Yost, S. R. & Voorhis, T. V. Electronic properties of disordered organic semiconductors via QM/MM simulations. Acc. Chem. Res. 43,

995–1004 (2010). Article  CAS  Google Scholar  * MacKenzie, R. C. I., Frost, J. M. & Nelson, J. A numerical study of mobility in thin films of fullerene derivatives. J. Chem. Phys. 132,

064904 (2010). Article  ADS  Google Scholar  * Yamada, T. et al. Revealing bipolar charge-transport property of 4,4′-N,N′-dicarbazolylbiphenyl (CBP) by quantum chemical calculations. Org.

Electron. 12, 169–178 (2011). Article  CAS  Google Scholar  * Rüchle, V. et al. Microscopic simulations of charge transport in disordered organic semiconductors. J. Chem. Theory Comput. 7,

3335–3345 (2011). Article  Google Scholar  * Li, H. et al. Experimental and theoretical study of the charge transport property of 4,4′-N,N′-dicarbazole-biphenyl. Sci. China Chem. 55,

2428–2432 (2012). Article  CAS  ADS  Google Scholar  * May, F. et al. Design rules for charge-transport efficient host materials for phosphorescent organic light-emitting diodes. J. Am.

Chem. Soc. 134, 13818–13822 (2012). Article  CAS  Google Scholar  * Friederich, P., Symalla, F., Meded, V., Neumann, T. & Wenzel, W. Ab initio treatment of disorder effects in amorphous

organic materials: Toward parameter free materials simulation. J. Chem. Theory Comput. 10, 3720–3725 (2014). Article  CAS  Google Scholar  * Suzuki, F. et al. Multiscale simulation of charge

transport in a host material, N,N′-dicarbazole-3,5-benzene (mCP), for organic light-emitting diodes. J. Mater. Chem. C 3, 5549–5555 (2015). Article  CAS  Google Scholar  * Marcus, R. A.

& Sutin, N. Electron transfers in chemistry and biology. Biochim. Biophys. Acta 811, 265–322 (1985). Article  CAS  Google Scholar  * Matsushima, H., Naka, S., Okada, H. & Onnagawa,

H. Organic electrophosphorescent devices with mixed hole transport material as emission layer. Curr. Appl. Phys. 5, 305–308 (2005). Article  ADS  Google Scholar  * Matsusue, N., Suzuki, Y.

& Naito, H. Charge carrier transport in neat thin films of phosphorescent iridium complexes. Jpn. J. Appl. Phys. 44, 3691 (2005). Article  CAS  ADS  Google Scholar  * Gill, W. D. Drift

mobilities in amorphous charge-transfer complexes of trinitrofluorenone and poly-n-vinylcarbazole. J. Appl. Phys. 43, 5033–5040 (1972). Article  ADS  Google Scholar  * Plimpton, S. Fast

parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995). Article  CAS  ADS  Google Scholar  * Frisch, M. J. et al.Gaussian 09, Revision C.01 and D.01.

Gaussian, Inc., Wallingford CT, 2009. Download references ACKNOWLEDGEMENTS The computation time on a supercomputer system was provided by the Institute for Chemical Research, Kyoto

University, Japan, and the Academic Center for Computing and Media Studies (ACCMS), Kyoto University, Japan. This work was partly supported by JSPS KAKENHI Grant Number 25248053. AUTHOR

INFORMATION AUTHORS AND AFFILIATIONS * Institute for Chemical Research, Kyoto University, Uji, 611-0011, Kyoto, Japan Hiroki Uratani, Shosei Kubo, Katsuyuki Shizu, Furitsu Suzuki, Tatsuya

Fukushima & Hironori Kaji Authors * Hiroki Uratani View author publications You can also search for this author inPubMed Google Scholar * Shosei Kubo View author publications You can

also search for this author inPubMed Google Scholar * Katsuyuki Shizu View author publications You can also search for this author inPubMed Google Scholar * Furitsu Suzuki View author

publications You can also search for this author inPubMed Google Scholar * Tatsuya Fukushima View author publications You can also search for this author inPubMed Google Scholar * Hironori

Kaji View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS H.K. planned and supervised the project. H.U. and S.K. performed the charge transport

simulations. H.K., K.S., and F.S. supervised the simulations. T.F. performed TOF experiments and H.K. supervised them. H.U., S.K., and H.K. wrote the paper. ETHICS DECLARATIONS COMPETING

INTERESTS The authors declare no competing financial interests. ELECTRONIC SUPPLEMENTARY MATERIAL SUPPLEMENTARY INFORMATION RIGHTS AND PERMISSIONS This work is licensed under a Creative

Commons Attribution 4.0 International License. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in

the credit line; if the material is not included under the Creative Commons license, users will need to obtain permission from the license holder to reproduce the material. To view a copy of

this license, visit http://creativecommons.org/licenses/by/4.0/ Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Uratani, H., Kubo, S., Shizu, K. _et al._ Detailed analysis of

charge transport in amorphous organic thin layer by multiscale simulation without any adjustable parameters. _Sci Rep_ 6, 39128 (2016). https://doi.org/10.1038/srep39128 Download citation *

Received: 19 August 2016 * Accepted: 17 November 2016 * Published: 21 December 2016 * DOI: https://doi.org/10.1038/srep39128 SHARE THIS ARTICLE Anyone you share the following link with will

be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt

content-sharing initiative