Reader TTS

ABSTRACT Recent progress in high power ultrafast short-wave and mid-wave infrared lasers has enabled gas-phase high harmonic generation (HHG) in the water window and beyond, as well as the

demonstration of HHG in condensed matter. In this Perspective, we discuss the recent advancements and future trends in generating and characterizing soft X-ray pulses from gas-phase HHG and

extreme ultraviolet (XUV) pulses from solid-state HHG. Then, we discuss their current and potential usage in time-resolved study of electron and nuclear dynamics in atomic, molecular and

condensed matters. SIMILAR CONTENT BEING VIEWED BY OTHERS ULTRAFAST HIGH-HARMONIC SPECTROSCOPY OF SOLIDS Article 10 October 2024 HOW TO OPTIMIZE HIGH-ORDER HARMONIC GENERATION IN GASES

Article 13 October 2022 BRIGHT CONTINUOUSLY TUNABLE VACUUM ULTRAVIOLET SOURCE FOR ULTRAFAST SPECTROSCOPY Article Open access 11 January 2024 INTRODUCTION Tabletop attosecond light sources in

the soft X-ray (SXR) spectral region based on high-harmonic generation are highly desirable in chemical and material sciences since they can spectroscopically identify specific elements, as

well as the oxidation states, charge states and even the spin states of those elements1. One of the important spectral regions is the “water window” (282–533 eV), which covers the atomic

K-shell excitation of carbon and oxygen. Although high harmonics in the water window were first generated with Ti:Sapphire lasers centered at 800 nm more than 20 years ago2,3, the X-ray

photon flux was too low for time-resolved applications. The mechanism of HHG in gases can be explained by the semiclassical three-step model4,5,6. When driving laser-field strength reaches

~108 V m−1, the bound electron in the atomic gas can tunnel through the Coulomb potential barrier and become a free electron. In the oscillating laser field, the free-electron wave packet

may return to its parent ion with the right time of birth. At recombination, the interference between the wave packets of the returning and bound electrons produces an oscillating dipole

that emits attosecond radiation. Returning electrons with various kinetic energy will recombine at different times giving rise to the chirp in the attosecond radiation7. This process repeats

twice for every optical cycle. The temporal beating of attosecond pulses results in the high-harmonic combs in the spectral domain. Empowered by the advances in driving lasers with center

wavelengths around 1.8 μm, soft X-ray high harmonics can be generated with a moderate intensity of 1014 W cm−2 (see Box 1 for details). Significant progress has recently been made in

developing attosecond light within the water window8. By spectrally broadening pulses from an Optical Parametric Amplifier (OPA) using a gas-filled hollow-core fiber9 or by broadband phase

matching in an Optical Parametric Chirped Pulse Amplifier (OPCPA)10, two-cycle, mJ-level pulses centered with 1 kHz repetition rate are now generated in many laboratories8. Seed pulses for

such light source can be produced by intra-pulse difference frequency generation (DFG)11 with stable carrier–envelope phase. In 2010 HHG has also been realized in condensed matter systems

using mid-infrared laser fields12. Since then, there has been significant attention on this field in investigating the underlying microscopic mechanism of solid-state HHG. Its promises

include stable attosecond light sources in compact forms and the possibility of attosecond metrology in solid-state materials13,14. A string of experimental surprises in solid-state HHG

include anomalous ellipticity dependence15, observation of a multiple plateau feature16 and orthogonally polarized high harmonics17. XUV harmonics from certain solid materials such as SiO2

crystals were found to be immune to fluctuations in the driving pump laser, providing a novel path toward stable attosecond pulses18. There are many exciting initiatives involving the

exploitation of microscopic generation processes in high-harmonic spectroscopy (HHS) of materials, including all-optical probing of the valence charge density in the real space15,19 and

electronic band structure in the reciprocal space20. Other unique features include the use of engineered materials at the nanometer scale to enhance, control, and manipulate the generation

process. HHS provides a novel approach to probe active electrons on nanoscale devices and on the surface state of quantum materials such as topological insulators. In this perspective, we

will first discuss the recent progress, challenges, and future trends in the development of gas-phase attosecond X-ray sources in the water window, followed by an extensive discussion on

their applications in molecular systems and condensed matter. Then, we will briefly review novel microscopic dynamics underlying solid-state HHG and discuss their applications in

high-harmonic spectroscopy of condensed matter systems both in and out-of-equilibrium. BOX 1 PHOTON ENERGY OF THE HIGH-HARMONIC SPECTRUM The highest photon energy (cutoff photon energy) from

gas-phase HHG can be estimated by $$\hbar \omega _{\mathrm{c}}\left[ {eV} \right] = I_{\mathrm{p}} + 3 \times 10^{ - 13}I_0\lambda _{\mathrm{L}}^2,$$ (1) where _I_p is the ionization

potential of the gas atom expressed in eV. The peak laser intensity \(I_0\) is in W cm−2, and the driving laser wavelength, \(\lambda _{\mathrm{L}}\), is in μm. Due to quantum diffusion, the

single-atom efficiency decreases with the driving laser wavelength (~\(\lambda _{\mathrm{L}}^{ - 6}\))41. The peak laser intensity is set for phase matching the HHG process to achieve high

photon flux, where the negative plasma dispersion is balanced by the unionized portion of the target gas. The calculated cutoff photon energy for noble gases at different laser wavelengths

is depicted in the figure below. This shows that the HHG spectrum can cover the water window by using short-wave infrared (SWIR) lasers144,145. Ionization induced plasma defocusing tends to

clamp laser intensity and reshape the radius profile146,147. The achievable SXR spectrum is therefore a collaborative result of atomic response and coherent buildup of high-harmonic

strength. WAVELENGTH SCALING OF HHG CUTOFF PHOTON ENERGY. Calculated cutoff photon energy of HHG under the phase-matching condition from various inert gases driven by lasers at different

center wavelengths. The purple square, blue dot, and red triangle indicate the achievable cutoff photon energy by using a 0.8 μm, 1.6 μm, and 2.5 μm driving laser, respectively. ISOLATED

WATER WINDOW X-RAY ATTOSECOND PULSES Single isolated attosecond pulses (IAP) are needed for conducting pump–probe measurements, such as attosecond streaking and attosecond

transient-absorption spectroscopy21,22,23,24. Various gating techniques have been developed to obtain such pulses (Table 1), and some of them have been implemented to generate isolated water

window X-ray bursts. SUBCYCLE GATING TECHNIQUES The simplest method to isolate a single attosecond burst from a few-cycle driving field is the amplitude gating (AG)25. In AG, with a proper

carrier–envelope phase value, the strongest half-cycle of the driving field will produce the attosecond burst with the broadest spectrum that exceeds all other bursts. By selecting a

suitable filter that transmits only this cutoff spectrum, an IAP can be achieved. AG has been adapted for the few-cycle short-wave infrared laser to demonstrate water window IAP10,26,27,28.

The width of the continuum near the cutoff can be estimated by $${\mathrm{\Delta }}\hbar \omega _{\mathrm{c}}[eV] = 3 \times 10^{ - 13}{\mathrm{\Delta }}I_{\mathrm{L}}\lambda

_{\mathrm{L}}^2,$$ (2) where \({\mathrm{\Delta }}I_{\mathrm{L}}\) is the intensity difference between the most intense half-cycle and the neighboring half-cycles of the driving laser field.

Future efforts will be made to increase this intensity by reducing the SWIR driving laser-pulse duration from the current state-of-the-art, ~two cycle, to just a single cycle. It is clear

from Eq. (2) that a much broader continuum can be obtained by using a longer wavelength driving laser for a given intensity difference. Highly efficient Chirped Pulse Amplification lasers

based on gain media such as Cr:ZnSe at 2.5 μm and Fe:ZnSe at 4 μm may extend the attosecond spectrum to O K-edge29,30,31. Spectral filtering methods, such as AG and ionization gating (IG)32,

can only isolate IAPs near the HHG spectrum cutoff. Techniques based on the temporal gating of the HHG process can generate an attosecond supercontinuum that covers both the plateau and

cutoff spectrum portion. The most common temporal gating method is polarization gating (PG)33,34. The influence of field ellipticity on HHG suppression increases as the driving wavelength

increases35. PG has the potential for generating ultra-broadband SXR pulses36, which may support even shorter attosecond sources in the future. Unfortunately, in PG, a substantial amount of

laser energy is wasted37. To reduce loss, the double optical gating (DOG) technique was proposed38. In DOG, a second harmonic field is added to break the fundamental field’s symmetry in a

process known as two-color gating39. A stronger IAP in the water window can be expected by applying the DOG40. CHARACTERIZATION OF ATTOSECOND PULSES Due to the low conversion efficiency

(~10−6) in gas-phase41 high-harmonic generation, attosecond pulse metrology relies on the photon ionization of the gas media by a weak IAP in the presence of a perturbative infrared (IR)

pulse. The photoelectron will gain (lose) energy by absorbing (emitting) one or more IR photons, depending on their relative delay. This technique, named attosecond streaking24, can

characterize an IAP after its birth. The unknown attosecond spectral phase information is encoded in the perturbed photoelectron energy spectrogram and can now be retrieved using the

frequency-resolved optical gating for complete reconstruction of attosecond bursts (FROG-CRAB) technique42, which is suitable for narrowband pulses. Alternative techniques are available for

characterizing broadband pulses43,44,45,46. Statistical noise in the streaking traces pose a challenge to reliable phase retrieval. For instance, large discrepancies are found in the pulse

duration and spectral phase when different phase retrieval schemes are applied47. Previous attosecond phase-retrieval schemes are based on time-consuming iterative algorithms. It is expected

that deep neuron network (DNN) algorithms will significantly cut down retrieval time46. Streaking measurements are affected by space charge effects. SWIR OPA/OPCPA lasers based on

high-average-power diode-pumped thin disc/slab Yb lasers48 provide a promising approach to deliver high-repetition-rate and high-flux attosecond pulses in the water window. This will

significantly improve the signal to noise ratio of streaking traces. ATTO-CHIRP COMPENSATION In HHG experiments, usually the short quantum pass survives through the macroscopic phase

matching resulting in attosecond pulses with a positive chirp49. Such chirp can be compensated by the negative group delay dispersion (GDD) of thin foils or neutral gases50. Recently,

isolated 53-as X-ray pulses whose spectra cover the 100–300 eV range have been characterized by attosecond streaking36. It is, however, difficult to compensate atto-chirp above the carbon

K-edge (282 eV) due to the lack of materials that exhibiting negative group velocity dispersion and low loss. It was illustrated theoretically that atto-chirp in the 300–1000 eV range can be

reduced by hydrogen gas or plasma with the proper pressure–length product given that the transmission of the gas or plasma is higher than 10%51,52. The GDD of neutral molecular hydrogen gas

at the photon energy \(\hbar \omega _{\mathrm{x}}\) can be expressed $$GDD_{{\mathrm{H}}_2}\left( {\hbar \omega _{\mathrm{x}}} \right) = 1.509 \times 10^9\frac{{PL}}{{\left( {\hbar \omega

_{\mathrm{x}}} \right)^3}},$$ (3) where pressure, _P_, is in atm, length, _L,_ is in cm, and photon energy, ℏ_ω_x,  is in eV. As an example, to compensate a 1600 as2 chirp at 365 eV, the

required pressure–length product is 54-atm cm, which is experimentally feasible. Hydrogen is preferred because of its low absorption in the SXR region compared with other materials. Uranium

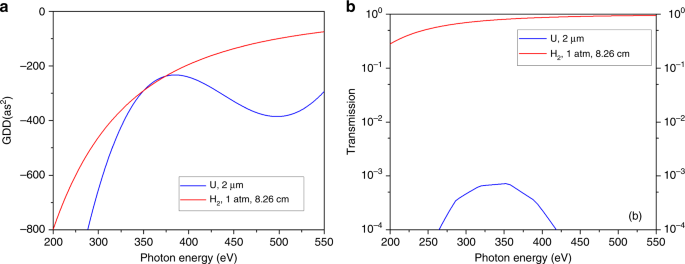
foil also exhibits negative GDD beyond 300 eV53, but its absorption is much higher than H2, as shown in Fig. 1. Their dispersion values are the same at 350 eV. The peak transmission of U

foil is <10−3 to compensate a 290 as2 atto-chirp, where the transmission of H2 is 80%. The transmission of ionized H2 is even better. Single-atom simulations based on the strong-field

approximation54,55,56,57,58 of high-harmonic generation have been performed to demonstrate feasibility of the atto-chirp compensation in the 300–500 eV51 and 530–1000 eV52 photon energy

regions. It has been shown that isolated attosecond pulses as short as 25-as are achievable when high-harmonic generation in helium is driven by single-cycle lasers centered at 1.7 μm or 3.2

 μm. The effectiveness of the chirp compensation by H2 plasma has been validated by simulations that account for phase macroscopic effects59. Experimental demonstration of such a chirp

compensation scheme may yield milestone results. Efforts need to be made to find schemes that can compensate the third-order phase error. Atto-chirp can also be reduced in the HHG process by

reshaping the driving field waveform using a multicolor synthesizer with controlled CEP and delay. Simulation has shown that nearly 60 pulses can be achieved in the 300–500 eV energy range

without atto-chirp compensation53. This technique is also promising for atto-chirp suppression in keV range. APPLICATIONS OF ATTOSECOND X-RAY SOURCES Attosecond XUV sources driven by

Ti:Sapphire lasers have been extensively used to study dynamics of electrons with less than 150 eV binding energy60. Femtosecond transient-absorption experiments with HHG sources at the

carbon K-edge have recently been reported, revealing molecular structural deformation processes that happen on a 50–100-fs timescale61,62. Attosecond water window X-ray sources have recently

enabled the observation of electronic processes in Ar atom at the L-edge (~250 eV)63, and in TiS2 films at the Ti L-edge (~460 eV)64. Ionization, vibration, and rotation dynamics have been

resolved in NO molecules using attosecond transient-absorption spectroscopy at the Nitrogen K-edge (~400 eV)65, as shown in Fig. 2. It is anticipated that more experiments will be conducted

to study charge dynamics in molecules and materials whose absorption edges are in the water window region66. Here, we discuss a few important applications. CHARGE MIGRATION IN MOLECULES AND

WAVE-PACKAGE DYNAMICS AT CONICAL INTERSECTIONS Comprehensive numerical simulations of electron dynamics in polyatomic molecules have predicted that when an electron is suddenly removed from

one end of a chain molecule, the hole can move to the other end in a few fs, often before electron–nuclear coupling sets in refs. 67,68. This purely electronic ultrafast dynamic process is

termed charge migration, a convention introduced in ref. 67, which should be distinguished from charge transfer, a slower spatial redistribution of electronic charge involving nuclear motion

that leads to charge relocation permanently from a donor to an acceptor. Charge migration is the first step in the fundamental process of electron transfer, which plays a role in

photochemistry, biology, and photovoltaics. Due to the coupling between the electron and nuclear motion, it may be possible to control the chemical reactivity of molecules by manipulating

their electronic motion as in the subfield dubbed attochemistry69. Observation of charge migration requires the preparation of a coherent superposition of electronic states and experimental

tools with sufficient temporal resolution to follow charge dynamics occurring on electronic timescales. This remains a grand challenge. Only a few experimental observations of charge motion

in molecules have so far been reported70,71. Numerical simulations predicted that charge migration occurs in many complex organic molecules67,68,72,73,74,75. However, almost none of them

have been verified experimentally due to the lack of experimental tools. The attosecond water window X-ray sources and transient-absorption spectroscopy provide a unique opportunity to

verify these predictions. They would allow probing charge migration in molecules containing C, N, and O atoms, the halogen atoms such as Cl, Br, and I, with attosecond time resolution.

Moreover, they would allow experimentalists to monitor the interplay of charge migration and nuclear motion on femtosecond timescales76. X-ray spectroscopy is element-specific and oxidation-

and charge-state sensitive77. Thus, SXR provide a powerful means to measure the charge states and charge migration between atoms. The individual atoms within a molecule exhibit X-ray energy

shifts, which depend on either the local chemical bonding environment or the electronic coherences themselves as charges migrate around a molecule. It is necessary to validate new

experimental tools by observing charge migration in simple molecules first and then to demonstrate their unique advantages by comparing them to previous methods. Charge migration in an

iodoacetylene cation has been observed in C2HI+ using high-harmonic spectroscopy71, where the high-harmonic XUV spectrum itself is measured as a function of pump–probe time delay after a

strong ionizing pulse. High-harmonic spectroscopy is based on the predictions of the semiclassical model of HHG that relate photon energy of a harmonic peak to the time difference between

the tunneling ionization (pump) and the photon emission (probe)78. When C2HI is ionized within a fraction of an optical cycle by the electric field of an intense infrared laser pulse, a

coherent electronic superposition state is created that can be expressed as an orbital mixture of the HOMO and HOMO-1 ground-state orbitals of the neutral molecule. $${\mathrm{\Psi

}}_{{\mathrm{MIX}}}\left( {{\mathbf{r}},t} \right) = \frac{1}{{\sqrt 2 }}\left[ {\phi _{{\mathrm{HOMO}}}\left( {\mathbf{r}} \right)e^{ - iE_{{\mathrm{HOMO}}}t/\hbar } + \phi

_{{\mathrm{HOMO}} - 1}\left( {\mathbf{r}} \right)e^{ - iE_{{\mathrm{HOMO}} - 1}t/\hbar }} \right].$$ (3) Numerical simulations show that ionization from the HOMO/HOMO-1 superposition of

states leads to characteristic charge oscillations with a period of ~2 fs. The dynamics of the electron hole reconstructed from the HHG measurements is shown in Fig. 3a71. By definition,

charge migration is periodic in the absence of dephasing or relaxation. Permanent charge transfer, on the other hand, requires electronic dephasing. One of the most important questions in

the study of charge migration is the lifetime of the electronic coherence that drives charge migration especially in the presence of vibrational motion. Numerical simulations suggest that

the charge migration induced by strong-field ionization lasts for at least 28 fs in C2HI+, as shown in Fig. 3b79. Such a prediction has not been confirmed by high-harmonic spectroscopy

measurements due to the limited time range of the measurements. The temporal window of the measurement is determined by the optical cycle of the driving lasers. This deficiency can be

addressed by X-ray transient absorption. Charge migration in C2HCl+, C2HBr+, and C2HI+ can be investigated using HHG-based attosecond water window X-rays. The scheme is shown in Fig. 3c.

Like in the HHG spectroscopy experiments, the electronic superposition state can be formed by ionization of the molecules with a strong IR laser pulse. However, here the hole motion will be

monitored by an X-ray probe using the transient-absorption method. Thanks to the broad X-ray supercontinuum from the HHG source, absorptions at the C K-edge and the I N-edge, Br M-edge, or

Cl L-edge can be measured simultaneously. Since the adjacent atoms of the two carbons are different, the absorption due to the core-to-valence transition should also be different. The motion

of the hole from one carbon to another carbon, and then to the iodine or chlorine will be monitored by the temporal variation of these absorptions. The temporal window in the X-ray

transient-absorption measurements can easily cover 100 fs or longer65. Therefore, the femtosecond decoherence process may be observed as well. The Born–Oppenheimer approximation is commonly

used in quantum chemistry to separate fast electronic dynamics from slow nuclear motions. However, it breaks down at conical intersections where two or more potential energy surfaces are

degenerate. Consequently, the coupling between electronic and nuclear motion must be considered in simulating the processes. Understanding charge dynamics around the conical intersections is

important for studying photosynthesis and other photon-initiated processes. Although energy surface crossings are ubiquitous in photochemistry80, material science81, and biology82, direct

observation of non-adiabatic dynamics at conical intersections with water window X-rays remains experimentally challenging. Neville et al. reported numerical simulations that show attosecond

transient absorption at the carbon K-edge is a powerful tool to study wave-package dynamics at a conical intersection of C2H2 molecules83. Experimental validation of theoretical predictions

of such simple molecules will pave the way to the investigation of more complex biological systems. PROBING CHARGE TRANSFER IN ORGANIC PHOTOVOLTAIC MATERIALS Organic photovoltaic materials

have received extensive research attention due to low fabrication cost, large area production, light weight, and flexibility. One type of organic solar cell consists of two different organic

molecules, namely donor and acceptor, that are mixed on the molecular level in a bulk-heterojunction structure. The most well-studied materials are poly(3-hexylthiophene-2,5-diyl) (P3HT) as

a donor, and [6,6]-phenyl-C61-butyric acid methyl ester (PC61BM) as an acceptor. The electron transfer from donor to acceptor needs to be fast to compete with lossy processes, such as

radiative and nonradiative recombination. Another important photovoltaic device is the dye-sensitized solar cell in which organic dyes such as N3, N719, and 2-picolinic acid are adsorbed

onto the electron transport layer such as TiO2 to enhance the charge transfer84,85, as illustrated in Fig. 4a. In a strongly coupled system, the charge injection from the organic dye

molecules to TiO2 takes place in 3–30 fs86,87, exceeding the instrument limit of femtosecond lasers that are the primary tool to time-resolve these processes at present88,89. Attosecond

pulses are poised to become a powerful technique to better understand such ultrafast dynamic processes involved in improving the efficiency and functionality of solar cell materials and

devices. Attosecond X-ray absorption spectroscopy can probe resonant transitions between core electrons and unoccupied states in the valence shells of molecules, as well as the valence and

conduction band of semiconductors. By utilizing a visible/UV pump with an attosecond soft X-ray probe, the electron transfer on timescales commensurate with electron and nuclei motion can be

investigated. For molecules adsorbed onto TiO2, a few-fs UV or visible pulse can be used as the pump. During the excitation, the absorption of LUMO at the C or N K-edges (~285 eV or ~400 

eV) should decrease. When the electrons move to the TiO2, the absorption in the conduction band probed by the Ti L-edge (~460 eV) should decrease. At the same time, the absorption of the

LUMO at the C or N K-edges should increase, as shown in Fig. 4. The attosecond X-ray transient absorption at the C, N, and Ti edges could be a unique tool to measure the electron-transfer

time of the strongly coupled system. The spatial localization of the 1s shell of C and N or the 2p shell of Ti means that excitation of electrons from these shells by attosecond X-ray pulses

to valence electronic states provides an atomic-site-specific probe of transient valence electron/hole populations. Similar pump–probe scheme can be applied to study charge transfer between

donors and acceptors in organic bulk-heterojunction solar cells. CONTROLLING DIELECTRIC PROPERTIES OF SOLIDS The electronic properties of matter can be modified drastically from its

equilibrium state by intense laser pulses. In 2011, a substantial redshift on the band-edge (>10% of the bandgap) was reported in bulk ZnO crystals subjected to intense mid-infrared laser

fields90. The shift was measured using a broadband ultraviolet light source in a pump–probe transient-absorption setting. In other independent studies, attosecond XUV pulses were used to

probe the dynamical absorption, on the subcycle timescale of the driving laser field, using thin Si91 as well as diamond92. Reversible semi-metallization of insulating materials has been

demonstrated in 2013, when SiO2 was illuminated with intense few-cycle near-infrared Ti:Sapphire-laser pulses93. A semi-metallization model was proposed to explain the transient-absorption

experiments at the Si L-edge (100–110 eV) that was covered by the spectral range of the Ti:Sapphire-laser-driven attosecond pulses. The attosecond water window X-ray source will allow

simultaneous measurements at both the Si L-edge and the O K-edge (533 eV) in transient-absorption experiments. This could provide the evidence of correlated charge motion at the Si and O

sites to deepen the understanding of the physical mechanism. Other materials such as diamond, BN, and Si3N4 can also be investigated in the similar manner. Controlling electrical

conductivity of solids at the timescale of an optical cycle allows a way to extend the speed of optoelectronics into the petahertz (1015 Hz) domain94, far exceeding the limit of current

field-effect transistor-based semiconductor electronics. This is critical to applications of high-speed all-optical signal processing and to the development of optical-field-effect

devices95,96. HIGH-HARMONIC SPECTROSCOPY OF CONDENSED MATTER High-harmonic spectroscopy has been widely used in atomic and molecular systems97, but that knowledge cannot be directly

implemented in condensed matter systems because underlying microscopic dynamics are different. In solid-state materials, the laser field-driven electrons are in the proximity of the periodic

Coulomb potential, so the usual strong-field approximation98, which is the foundation of the three-step re-collision model4,5, becomes qualitatively invalid. Recently, a real-space electron

trajectory model has been developed that considers the role of the periodic potential on the semiclassical motion of the electron and includes the possibility of coherent collisions with

the neighboring atomic sites15,19. In this picture, harmonic emission becomes stronger (weaker) when electron trajectories strike (miss) the atomic cores of nearest-neighbor atoms. A typical

experimental setup for such spectroscopy is shown in Fig. 5a. In this particular example, a wide-bandgap MgO crystal is pumped with a NIR laser pulse, and XUV harmonics are analyzed as a

function of crystal orientation and laser ellipticity. The real-space electron trajectory model describes the observed crystal orientation dependence, ellipticity dependence, and therefore

provides the opportunity to probe the valence charge density distributions inside bulk materials in all-optical settings15,19. Because the electron trajectories can be controlled by laser

parameters (field strength, polarization, and wavelength), the real-space picture provides a powerful, all-optical, and tabletop approach to probe valence charge density distributions in

bulk materials. Dynamics in solid-state materials are often described in reciprocal or momentum space. In this framework, non-perturbative high-order harmonics originate mainly from two

channels, namely the intraband nonlinear current and the interband polarization, as shown schematically represented by simple cosine bands of opposite mass across a direct bandgap in Fig. 

614. Initially, the valence band is full, and the conduction band is empty. Upon photoexcitation, an electron–hole pair is created at the zone center (_k_ = 0) by tunneling across the

minimum bandgap. Then, both the electron and the hole are accelerated by the electric field towards the zone edge. At high-enough peak-field strength, the electrons can reach the zone edge

(_k_ = π/a, where a is the lattice constant) and be Bragg diffracted, even multiple times every half-cycle. For nonparabolic bands such intraband current can radiate at much higher

frequencies than the fundamental driving frequency. Similarly, the electron and hole can recombine at later time at higher crystal momentum locations, as shown by the dashed arrow, releasing

a high-energy photon99,100. Often at high peak fields these dynamics get coupled. Through the intraband channel, the dispersion of a responsible conduction band can be probed, as proposed

by Ghimire et al. 12 and implemented in detail by Luu et al. using quartz crystal recently101. In contrast, the interband channel involves intrinsic atto-chirp because there are unique

recombination paths at different energies and momenta corresponding to different harmonic orders99,100. Therefore, by measuring the atto-chirp of high harmonics from the interband channel,

the momentum-dependent bandgap can be deduced, as shown in ZnO crystal20. At sufficient high-harmonic peak intensities, transitions to higher-lying conduction bands is possible and that

could lead to secondary plateau in high-harmonic spectrum, as observed in rare-gas solids16 and in room temperature solids, such as MgO and SiO2 crystal102. Similarly, depending on the

system, lower-lying valence bands may also contribute, as understood by analysing the terahertz-field driven harmonics in GaSe crystal103,104. Therefore, in the momentum-space framework,

high-harmonic spectroscopy also presents a novel, all-optical approach for probing electronic band structure, including away from the zone center. For these measurements it may be essential

to separate propagation effects. DIPOLE PHASE AND PROPAGATION EFFECTS One of the unique challenges in probing atto-chirp, and for HHS in general, is separating the strong propagation

effects. This is because in bulk samples, the intense pump laser pulse accumulates a significant nonlinear phase as it propagates from the entrance to the exit end from where the above

bandgap harmonics are typically emitted from. Modeling the effects of the nonlinear phase, such as the effects from \(\chi ^{\left( 3 \right)}\) on to the fundamental laser field and

consequently to high-order harmonics, is complex. Recently, non-perturbative high harmonics were also observed in the backward reflection geometry, which avoids propagation effects105. In

the following passage, we briefly discuss the results of attosecond interferometry in a homodyne configuration that was performed in both a reflection and a transmission geometry106. The

experimental setup is shown in Fig. 7. Here, the main idea is that XUV harmonics are generated in two spatially separated foci, but harmonics overlap in the far field and self-referenced

interferometry is performed. The measured fringe shifts in the reflected harmonics were reproduced by separating the interband polarization in a strongly driven two-level system. The fringe

shifts in transmission are overwhelmed by propagation effects, as  the shifts are much larger than the predictions from microscopic model and are opposite in direction. Intriguingly, the

measured fringe shifts in reflection mode are source material-dependent, as XUV harmonics from MgO crystal show much larger shifts compared with those from SiO2. This is in contrast to the

gas-phase HHG where, for high-enough photon energies, the dipole phase is independent of the target atom107. While it is not immediately clear what specific features of the electronic

structure make the dipole phase shift differently in these materials, the experimental results clearly show the sensitivity of high-harmonic spectroscopy. Along this line, future experiments

can utilize this platform in many ways; for example, by referencing novel high-harmonics sources such as from solids, nanostructures, or liquid media with respect to that from well-studied

gas-phase sources in a heterodyne configuration. HHS could also be used to probe impurities in semiconductors with high spatial resolution. COMPACT XUV LIGHT SOURCE BASED ON SOLID-STATE HHG

Recent results have shown that solid-state HHG has the following main advantages when compared with HHG from dilute gas targets: (i) lower prerequisite on driving peak intensity because

solid-state HHG threshold on dielectrics is around 1012 W cm−216, (ii) the XUV waveform produced by some solid-state materials are found largely immune to fluctuations in the driving

fields18, and (iii) the use of tailored nanostructures, such as metal–sapphire bow tie108, or the use of heterostructures, such as epsilon-near-zero materials, improves the HHG efficiency

substantially109. The use of zone plates as a source material has provided the ability to focus the high-harmonic beams directly without the use of additional optics110 that could be

extremely demanding in the XUV wavelength range. Solid-state HHG setups do not require sophisticated high-vacuum pumping systems because of no gas load. Polarization of solid-state harmonics

can be controlled by taking advantage of anisotropy in the electronic band structure111 as well as the Berry phase in non-centrosymmetric crystals, such as SiO2112. Circularly polarized

harmonics have been demonstrated, at least in the visible wavelength range113. One drawback of solid-state HHG when compared with gas-phase HHG is that the high-energy cutoff is limited by

the material’s damage threshold, which in the case of wide-bandgap dielectric, has reached a ceiling of ~40 eV16. Further extension to higher photon energy range might be possible by the use

of ultra-short driving pulses. The rapid development of few-cycle, high-repetition-rate light sources, including optical parametric chirped-pulse amplifiers, can provide suitable pump

sources for solid-state HHG. With field enhancement in nanostructures in wide-gap materials108, high-harmonic XUV light sources based on laser oscillators or OPCPAs operating at

high-repetition rates appear promising. The dispersion of solids in the infrared pump wavelength range can be engineered, for example, by introducing waveguides114, photonic crystal

structures115 and metamaterials116, and by utilizing epsilon-near-zero effects through doping109. The phase matching between pump fields and harmonics in a specific spectral range could be

optimized, which could lead to enhanced generation efficiency. In the high photon energy regime, the absorption of harmonics above a material’s bandgap reduces the effective generation

thickness to the absorption length—usually on the order of ten nanometers for XUV harmonics—thus greatly limiting the HHG efficiency. For sufficiently high photon energy ranges, the

absorption of high-energy photons could be alleviated. For example, for just under 100 eV, silicon’s attenuation length is expected to be around 500 nm. If phase matching can also be

achieved, for example by taking advantage of a tunable refractive index in epsilon-near-zero materials, solid-state HHG could also reach the SXR photon energy range. ALL-OPTICAL PROBING OF

ULTRAFAST DYNAMICS IN MATERIALS There are initiatives aimed at testing the potential of the HHG process in probing structure and ultrafast dynamics in condensed matter systems. Examples of

ultrafast phenomena include insulator to metal phase transitions, strongly correlated electron dynamics117, and topological phase transitions in quantum materials118. Theoretical predictions

are emerging, which includes calculations on one dimensional model systems focusing on how the trivial to topological phase transition dramatically enhances the efficiency of the HHG

process118 and two-dimensional Haldane model system focusing on how HHG could probe topological invariants119,120. This particular aspect, as well as just how phase transitions and

correlations manipulate the HHG process at the microscopic level on novel quantum materials, are outstanding questions at this time121. A nominal experimental setup could be a pump–probe

scheme, wherein an ultrafast pump laser initiates a phase transition, and a strong-field probe pulse produces high harmonics from the active medium as a function of pump–probe. Currently,

angle-resolved photoemission spectroscopy (ARPES) is the standard spectroscopic method to measure the band structure. However, since it is based on the detection of electrons, it has

stringent experimental requirements such as ultra-high-vacuum and ultra-clean sample environments. Its temporal resolution in a pump–probe setting has been demonstrated only down to about

tens of femtoseconds122. Similarly, time-resolved X-ray absorption/diffraction techniques also have limitations, usually >50 fs, because of the temporal jitter between the pump laser and

the X-ray source123. Being an all-optical method, high-harmonic spectroscopy provides unprecedented time resolution and also much of these measurements can be performed in ambient

conditions, i.e., without the need for vacuum apparatus, especially if the pump lasers are in the mid-infrared wavelength range. High harmonics provide a novel approach to probe active

electronics in two-dimensional materials and heterostructures. Finally, we note that so far the solid-state HHG theory is largely based on single active electron approximation, either

through solving time-dependent Schrödinger equations (TDSE)99,100,124 or through semiconductor Bloch equations (SBE)103,125. Many-body effects such as electron-electron correlations and

dephasing are largely ignored while the latter is implemented just phenomenologically. Therefore, more predictive theories that consider correlations and multiple electronic bands are highly

desired. One path forward could be through the ab initio approach based on time-dependent density-functional theory (TDFT), which could in principle consider the full band structure and

joint density of states126. SUMMARY AND OUTLOOK The recent breakthroughs in attosecond “water window” X-ray sources open the door to game-changing applications. The combination of

unprecedented time resolution with element-specific spectroscopy provides a unique opportunity for studying charge and nuclear dynamics in organic molecules and materials containing C, N, O,

and other important elements and may help in understanding the charge transfer mechanism in solar cell materials. So far, transient-absorption spectroscopy measurements have been

demonstrated in the water window with attosecond time resolution. It is expected that attosecond photoelectron spectroscopy127, attosecond coherent diffraction imaging128, attosecond

reflection spectroscopy129, as well as other time-resolved techniques130, such as HHG-based ARPES131 and Cold Target Recoil Ion Momentum Spectroscopy (COLTRIMS) apparatus132 will be

implemented beyond the Carbon K-edge. Currently, the attosecond pulse energy from HHG source is too weak to populate excited state in the atoms or molecules. The benefit of more energetic

attosecond pulses is the possibility to perform true attosecond-pump–attosecond-probe experiments, where excitations are fulfilled through direct core level transition by absorbing a single

XUV/SXR photon. Major efforts towards enhancing HHG efficiency include two-color driving fields as well as the use of MWIR. In the latter, it is easier to individually control the three

steps of the HHG process133 because of the long laser cycles. Recently, a fundamentally different technique for producing attosecond pulses has emerged at X-ray free-electron lasers,

particularly at the Linac Coherent Light Source (LCLS)134,135. Accelerator-based sources typically provide substantial flux so they will enable a new class of experiments, including true

attosecond-pump and attosecond-probe capabilities. Solid-state HHG has been realized in a wide range of materials and harmonic spectrum has reached ~40 eV. These results have shown promises

for stable attosecond pulses in compact experimental setups, along with the novel all-optical method to directly probe the structure and dynamics of the source material. Because of the

modest requirements in the peak intensity (1011–1013 W cm−2) solid-state HHG could possibly be pumped with next-generation high-repetition rate fiber laser systems such that the total flux

of XUV photons can be increased significantly. The underlying microscopic generation mechanism can be utilized to probe both structure and dynamics of the source materials. When we consider

the fact that the driven electron motion in solids must be governed by their band structure, high harmonics bear the imprint of the electronic band structure of the solid. A unique

capability of HHG approach is the ability to access conduction bands lying higher than the Fermi level, and yet the polarization response and spectral phase of harmonics provides additional

sensitivity such Berry curvature and topology, which are not directly accessible with conventional spectroscopic methods such as ARPES. While the community is still in the process of

developing the detailed decoding procedure, high-harmonic spectroscopy has quickly become an attractive area of attosecond science and technology. With the emergence of new generation

tabletop attosecond light sources based on both gas-phase and solid-phase HHG and novel time-resolved experimental and theoretical tools in a wide spectral range for studying dynamics in

isolated molecules and condensed-phase materials, we now stand at the threshold of another revolution in attosecond science and technology. REFERENCES * Chen, L. X. Probing transient

molecular structures in photochemical processes using laser-initiated time-resolved X-ray absorption spectroscopy. _Annu. Rev. Phys. Chem._ 56, 221–254 (2005). Article  ADS  CAS  PubMed 

Google Scholar  * Chang, Z. H., Rundquist, A., Wang, H. W., Murnane, M. M. & Kapteyn, H. C. Generation of coherent soft X rays at 2.7 nm using high harmonics. _Phys. Rev. Lett._ 79,

2967–2970 (1997). Article  ADS  CAS  Google Scholar  * Spielmann, C. et al. Generation of coherent X-rays in the water window using 5-femtosecond laser pulses. _Science_ 278, 661–664 (1997).

Article  ADS  CAS  Google Scholar  * Corkum, P. B. Plasma perspective on strong field multiphoton ionization. _Phys. Rev. Lett._ 71, 1994 (1993). Article  ADS  CAS  PubMed  Google Scholar 

* Schafer, K. J., Yang, B., DiMauro, L. F. & Kulander, K. C. Above threshold ionization beyond the high harmonic cutoff. _Phys. Rev. Lett._ 70, 1599–1602 (1993). Article  ADS  CAS 

PubMed  Google Scholar  * Lewenstein, M., Balcou, P., Ivanov, M. Y., L’huillier, A. & Corkum, P. B. Theory of high-harmonic generation by low-frequency laser fields. _Phys. Rev. A_ 49,

2117 (1994). Article  ADS  CAS  PubMed  Google Scholar  * Mairesse, Y. et al. Attosecond synchronization of high-harmonic soft x-rays. _Science_ 302, 1540–1543 (2003). Article  ADS  CAS 

PubMed  Google Scholar  * Ren, X. et al. Attosecond light sources in the water window. _J. Opt._ 20, 023001 (2018). Article  ADS  CAS  Google Scholar  * Schmidt, B. E. et al. CEP stable 1.6

cycle laser pulses at 1.8 μm. _Opt. express_ 19, 6858–6864 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Ishii, N. et al. Sub-two-cycle, carrier-envelope phase-stable, intense optical

pulses at 1.6 μm from a BiB3O6 optical parametric chirped-pulse amplifier. _Opt. Lett._ 37, 4182–4184 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Baltuška, A., Fuji, T. &

Kobayashi, T. Controlling the carrier-envelope phase of ultrashort light pulses with optical parametric amplifiers. _Phys. Rev. Lett._ 88, 133901 (2002). Article  ADS  PubMed  CAS  Google

Scholar  * Ghimire, S. et al. Observation of high-order harmonic generation in a bulk crystal. _Nat. Phys._ 7, 138–141 (2011). Article  CAS  Google Scholar  * Vampa, G. & Brabec, T.

Merge of high harmonic generation from gases and solids and its implications for attosecond science. _J. Phys. B: At., Mol. Optical Phys._ 50, 083001 (2017). Article  ADS  CAS  Google

Scholar  * Ghimire, S. & Reis, D. A. High-harmonic generation from solids. _Nat. Phys._ 15, 10–16 (2019). Article  CAS  Google Scholar  * You, Y. S., Reis, D. A. & Ghimire, S.

Anisotropic high-harmonic generation in bulk crystals. _Nat. Phys._ 13, 345–349 (2017). Article  CAS  Google Scholar  * Ndabashimiye, G. et al. Solid-state harmonics beyond the atomic limit.

_Nature_ 534, 520–523 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Liu, H. et al. High-harmonic generation from an atomically thin semiconductor. _Nat. Phys._ 13, 262–265 (2017).

Article  CAS  Google Scholar  * Garg, M., Kim, H. Y. & Goulielmakis, E. Ultimate waveform reproducibility of extreme-ultraviolet pulses by high-harmonic generation in quartz. _Nat.

Photonics_ 12, 291–296 (2018). Article  ADS  CAS  Google Scholar  * You, Y. S., Cunningham, E., Reis, D. A. & Ghimire, S. Probing periodic potential of crystals via strong-field

re-scattering. _J. Phys. B: At., Mol. Optical Phys._ 51, 114002 (2018). Article  ADS  CAS  Google Scholar  * Vampa, G. et al. All-optical reconstruction of crystal band structure. _Phys.

Rev. Lett._ 115, 193603 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Chang, Z., Corkum, P. B. & Leone, S. R. Attosecond optics and technology: progress to date and future

prospects [Invited]. _JOSA B_ 33, 1081–1097 (2016). Article  ADS  CAS  Google Scholar  * Wang, H. et al. Attosecond time-resolved autoionization of argon. _Phys. Rev. Lett._ 105, 143002

(2010). Article  ADS  PubMed  CAS  Google Scholar  * Goulielmakis, E. et al. Real-time observation of valence electron motion. _Nature_ 466, 739–U737 (2010). Article  ADS  CAS  PubMed 

Google Scholar  * Itatani, J. et al. Attosecond streak camera. _Phys. Rev. Lett._ 88, 173903 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Hentschel, M. et al. Attosecond metrology.

_Nature_ 414, 509–513 (2001). Article  ADS  CAS  PubMed  Google Scholar  * Cousin, S. L. et al. Attosecond streaking in the water window: a new regime of attosecond pulse characterization.

_Phys. Rev. X_ 7, 041030 (2017). Google Scholar  * Teichmann, S. M., Silva, F., Cousin, S. L., Hemmer, M. & Biegert, J. 0.5-keV Soft X-ray attosecond continua. _Nat. Commun._ 7, 11493

(2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Ishii, N. et al. Carrier-envelope phase-dependent high harmonic generation in the water window using few-cycle infrared

pulses. _Nat. Commun._ 5, 1–6 (2014). * Ren, X., Mach, L. H., Yin, Y., Wang, Y. & Chang, Z. Generation of 1 kHz, 2.3 mJ, 88 fs, 2.5 µm pulses from a Cr2+:ZnSe chirped pulse amplifier.

_Opt. Lett._ 43, 3381–3384 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Wu, Y. et al. Generation of few-cycle multi-millijoule 2.5 μm pulses from a single-stage Cr2+:ZnSe amplifier.

_Sci. Rep._ 10, 7775 (2020). Article  CAS  PubMed  PubMed Central  ADS  Google Scholar  * Migal, E. et al. 3.5-mJ 150-fs Fe: ZnSe hybrid mid-IR femtosecond laser at 4.4 μm for driving

extreme nonlinear optics. _Opt. Lett._ 44, 2550–2553 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Abel, M. J. et al. Isolated attosecond pulses from ionization gating of

high-harmonic emission. _Chem. Phys._ 366, 9–14 (2009). Article  CAS  Google Scholar  * Corkum, P., Burnett, N. & Ivanov, M. Y. Subfemtosecond pulses. _Opt. Lett._ 19, 1870–1872 (1994).

Article  ADS  CAS  PubMed  Google Scholar  * Chang, Z. Single attosecond pulse and xuv supercontinuum in the high-order harmonic plateau. _Phys. Rev. A_ 70, 043802 (2004). Article  ADS  CAS

  Google Scholar  * Möller, M. et al. Dependence of high-order-harmonic-generation yield on driving-laser ellipticity. _Phys. Rev. A_ 86, 011401 (2012). Article  ADS  CAS  Google Scholar  *

Li, J. et al. 53-attosecond X-ray pulses reach the carbon K-edge. _Nat. Commun._ 8, 186 (2017). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Li, J. et al. Polarization gating

of high harmonic generation in the water window. _Appl. Phys. Lett._ 108, 231102 (2016). Article  ADS  CAS  Google Scholar  * Mashiko, H. et al. Double optical gating of high-order harmonic

generation with carrier-envelope phase stabilized lasers. _Phys. Rev. Lett._ 100, 103906 (2008). Article  ADS  PubMed  CAS  Google Scholar  * Mauritsson, J. et al. Attosecond pulse trains

generated using two color laser fields. _Phys. Rev. Lett._ 97, 013001 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Li, J. et al. Double optical gating for generating high flux

isolated attosecond pulses in the soft X-ray regime. _Opt. Express_ 27, 30280–30286 (2019). Article  ADS  PubMed  CAS  Google Scholar  * Shiner, A. D. et al. Wavelength scaling of high

harmonic generation efficiency. _Phys. Rev. Lett._ 103, 073902 (2009). Article  ADS  CAS  PubMed  Google Scholar  * Mairesse, Y. & Quéré, F. Frequency-resolved optical gating for

complete reconstruction of attosecond bursts. _Phys. Rev. A_ 71, 011401 (2005). Article  ADS  CAS  Google Scholar  * Chini, M., Gilbertson, S., Khan, S. D. & Chang, Z. Characterizing

ultrabroadband attosecond lasers. _Opt. express_ 18, 13006–13016 (2010). Article  ADS  PubMed  Google Scholar  * Keathley, P. D., Bhardwaj, S., Moses, J., Laurent, G. & Kärtner, F. X.

Volkov transform generalized projection algorithm for attosecond pulse characterization. _N. J. Phys._ 18, 073009 (2016). Article  Google Scholar  * Zhao, X., Wei, H., Wu, Y. & Lin, C.

D. Phase-retrieval algorithm for the characterization of broadband single attosecond pulses. _Phys. Rev. A_ 95, 043407 (2017). Article  ADS  Google Scholar  * White, J. & Chang, Z.

Attosecond streaking phase retrieval with neural network. _Opt. Express_ 27, 4799–4807 (2019). Article  ADS  CAS  PubMed  Google Scholar  * Xi, Z., Su-Ju, W., Wei-Wei, Y. & Hui, W.

Metrology of time-domain soft X-ray attosecond pulses and re-evaluation of pulse durations of three recent experiments. _Phys. Rev. Applied_ 13, 034043 (2020). Article  ADS  Google Scholar 

* Pupeikis, J. et al. Water window soft x-ray source enabled by a 25 W few-cycle 2.2 µm OPCPA at 100 kHz. _Optica_ 7, 168–171 (2020). Article  ADS  Google Scholar  * Antoine, P., L’Huillier,

A. & Lewenstein, M. Attosecond pulse trains using high-order harmonics. _Phys. Rev. Lett._ 77, 1234–1237 (1996). Article  ADS  CAS  PubMed  Google Scholar  * Kim, K. T., Kim, C. M.,

Baik, M.-G., Umesh, G. & Nam, C. H. Single sub- 50-attosecond pulse generation from chirp-compensated harmonic radiation using material dispersion. _Phys. Rev. A_ 69, 051805 (2004).

Article  ADS  CAS  Google Scholar  * Chang, Z. Attosecond chirp compensation in water window by plasma dispersion. _Opt. Express_ 26, 33238–33244 (2018). Article  ADS  CAS  PubMed  Google

Scholar  * Chang, Z. Compensating chirp of attosecond X-ray pulses by a neutral hydrogen gas. _OSA Contin._ 2, 314–319 (2019). Article  CAS  Google Scholar  * Fu, Y., Yuan, H., Midorikawa,

K., Lan, P. & Takahashi, E. Towards GW-scale isolated attosecond pulse far beyond carbon K-edge driven by mid-infrared waveform synthesizer. _Appl. Sci._ 8, 2451 (2018). Article  CAS 

Google Scholar  * Keldysh, L. Ionization in the field of a strong electromagnetic wave. _Sov. Phys. JETP_ 20, 1307–1314 (1965). Google Scholar  * Faisal, F. H. M. Multiple absorption of

laser photons by atoms. _J. Phys. B: At. Mol. Phys._ 6, L89–L92 (1973). Article  ADS  Google Scholar  * Reiss, H. R. Effect of an intense electromagnetic field on a weakly bound system.

_Phys. Rev. A_ 22, 1786–1813 (1980). Article  ADS  CAS  Google Scholar  * Milošević, D. B., Paulus, G. G., Bauer, D. & Becker, W. Above-threshold ionization by few-cycle pulses. _J.

Phys. B: At., Mol. Optical Phys._ 39, R203–R262 (2006). Article  ADS  CAS  Google Scholar  * Popruzhenko, S. V. Keldysh theory of strong field ionization: history, applications, difficulties

and perspectives. _J. Phys. B: At., Mol. Optical Phys._ 47, 204001 (2014). Article  ADS  CAS  Google Scholar  * Kovács, K. & Tosa, V. Macroscopic attosecond chirp compensation. _Opt.

Express_ 27, 21872–21879 (2019). Article  ADS  PubMed  Google Scholar  * Leone, S. R. et al. What will it take to observe processes in ‘real time’? _Nat. Photonics_ 8, 162–166 (2014).

Article  ADS  CAS  Google Scholar  * Attar, A. R. et al. Femtosecond x-ray spectroscopy of an electrocyclic ring-opening reaction. _Science_ 356, 54–59 (2017). Article  ADS  CAS  PubMed 

Google Scholar  * Pertot, Y. et al. Time-resolved x-ray absorption spectroscopy with a water window high-harmonic source. _Science_ 355, 264–267 (2017). Article  ADS  CAS  PubMed  Google

Scholar  * Chew, A. et al. Attosecond transient absorption spectrum of argon at the L2, 3 edge. _Phys. Rev. A_ 97, 031407 (2018). Article  ADS  CAS  Google Scholar  * Buades, B. et al.

Attosecond-resolved petahertz carrier motion in semi-metallic TiS2. Preprint at https://arxiv.org/abs/1808.06493 (2018). * Saito, N. et al. Real-time observation of electronic, vibrational,

and rotational dynamics in nitric oxide with attosecond soft x-ray pulses at 400 eV. _Optica_ 6, 1542–1546 (2019). Article  ADS  Google Scholar  * Young, L. et al. Roadmap of ultrafast x-ray

atomic and molecular physics. _J. Phys. B: At., Mol. Optical Phys._ 51, 032003 (2018). Article  ADS  CAS  Google Scholar  * Cederbaum, L. S. & Zobeley, J. Ultrafast charge migration by

electron correlation. _Chem. Phys. Lett._ 307, 205–210 (1999). Article  ADS  CAS  Google Scholar  * Remacle, F., Levine, R., Schlag, E. & Weinkauf, R. Electronic control of site

selective reactivity: a model combining charge migration and dissociation. _J. Phys. Chem. A_ 103, 10149–10158 (1999). Article  CAS  Google Scholar  * Lépine, F., Ivanov, M. Y. &

Vrakking, M. J. Attosecond molecular dynamics: fact or fiction? _Nat. Photonics_ 8, 195 (2014). Article  ADS  CAS  Google Scholar  * Calegari, F. et al. Ultrafast electron dynamics in

phenylalanine initiated by attosecond pulses. _Science_ 346, 336–339 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Kraus, P. et al. Measurement and laser control of attosecond charge

migration in ionized iodoacetylene. _Science_ 350, 790–795 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Kuleff, A. I., Lünnemann, S. & Cederbaum, L. S. Ultrafast charge migration

following valence ionization of 4-methylphenol: jumping over the aromatic ring. _J. Phys. Chem. A_ 114, 8676–8679 (2010). Article  CAS  PubMed  Google Scholar  * Kuleff, A. I., Lünnemann,

S. & Cederbaum, L. S. Electron-correlation-driven charge migration in oligopeptides. _Chem. Phys._ 414, 100–105 (2013). Article  CAS  Google Scholar  * Kuleff, A. I., Kryzhevoi, N. V.,

Pernpointner, M. & Cederbaum, L. S. Core ionization initiates subfemtosecond charge migration in the valence shell of molecules. _Phys. Rev. Lett._ 117, 093002 (2016). Article  ADS 

PubMed  CAS  Google Scholar  * Despré, V., Golubev, N. V. & Kuleff, A. I. Charge migration in propiolic acid: a full quantum dynamical study. _Phys. Rev. Lett._ 121, 203002 (2018).

Article  ADS  PubMed  Google Scholar  * Vacher, M., Bearpark, M. J., Robb, M. A. & Malhado, J. P. Electron dynamics upon ionization of polyatomic molecules: coupling to quantum nuclear

motion and decoherence. _Phys. Rev. Lett._ 118, 083001 (2017). Article  ADS  PubMed  Google Scholar  * Ramasesha, K., Leone, S. R. & Neumark, D. M. Real-time probing of electron dynamics

using attosecond time-resolved spectroscopy. _Annu. Rev. Phys. Chem._ 67, 41–63 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Peng, P., Marceau, C. & Villeneuve, D. M. Attosecond

imaging of molecules using high harmonic spectroscopy. _Nat. Rev. Phys._ 1, 144–155 (2019). Article  Google Scholar  * Wörner, H. J. et al. Charge migration and charge transfer in molecular

systems. _Struct. Dyn._ 4, 061508 (2017). Article  PubMed  PubMed Central  CAS  Google Scholar  * Levine, B. G. & Martínez, T. J. Isomerization through conical intersections. _Annu Rev.

Phys. Chem._ 58, 613–634 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Shu, Y., Fales, B. S. & Levine, B. G. Defect-induced conical intersections promote nonradiative

recombination. _Nano Lett._ 15, 6247–6253 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Polli, D. et al. Conical intersection dynamics of the primary photoisomerization event in

vision. _Nature_ 467, 440–443 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Neville, S. P., Chergui, M., Stolow, A. & Schuurman, M. S. Ultrafast X-ray spectroscopy of conical

intersections. _Phys. Rev. Lett._ 120, 243001 (2018). Article  ADS  PubMed  Google Scholar  * Hagfeldt, A., Boschloo, G., Sun, L., Kloo, L. & Pettersson, H. Dye-sensitized solar cells.

_Chem. Rev._ 110, 6595–6663 (2010). Article  CAS  PubMed  Google Scholar  * Listorti, A., O’Regan, B. & Durrant, J. R. Electron transfer dynamics in dye-sensitized solar cells. _Chem.

Mater._ 23, 3381–3399 (2011). Article  CAS  Google Scholar  * Huber, R., Moser, J.-E., Grätzel, M. & Wachtveitl, J. Real-time observation of photoinduced adiabatic electron transfer in

strongly coupled dye/semiconductor colloidal systems with a 6 fs time constant. _J. Phys. Chem. B_ 106, 6494–6499 (2002). Article  CAS  Google Scholar  * Schnadt, J. et al. Experimental

evidence for sub-3-fs charge transfer from an aromatic adsorbate to a semiconductor. _Nature_ 418, 620–623 (2002). Article  ADS  CAS  PubMed  Google Scholar  * Song, Y., Clafton, S. N.,

Pensack, R. D., Kee, T. W. & Scholes, G. D. Vibrational coherence probes the mechanism of ultrafast electron transfer in polymer–fullerene blends. _Nat. Commun._ 5, 4933 (2014). Article

  ADS  PubMed  CAS  Google Scholar  * Song, Y., Hellmann, C., Stingelin, N. & Scholes, G. D. The separation of vibrational coherence from ground- and excited-electronic states in P3HT

film. _J. Chem. Phys._ 142, 212410 (2015). Article  ADS  PubMed  CAS  Google Scholar  * Ghimire, S. et al. Redshift in the optical absorption of ZnO single crystals in the presence of an

intense midinfrared laser field. _Phys. Rev. Lett._ 107, 167407 (2011). Article  ADS  PubMed  CAS  Google Scholar  * Schultze, M. et al. Attosecond band-gap dynamics in silicon. _Science_

346, 1348–1352 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Lucchini, M. et al. Attosecond dynamical Franz-Keldysh effect in polycrystalline diamond. _Science_ 353, 916–919 (2016).

Article  ADS  CAS  PubMed  Google Scholar  * Schultze, M. et al. Controlling dielectrics with the electric field of light. _Nature_ 493, 75–78 (2013). Article  ADS  PubMed  CAS  Google

Scholar  * Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. _Nat. Photonics_ 8, 205–213 (2014). Article  ADS  CAS  Google Scholar  *

Kong, X., Wang, F., Zhang, X., Liu, Z. & Pang S. Controlling dielectric properties of cBN by an ultrashort double-pulse light. _Phys. Lett. A_ 384, 126125 (2019). * Goulielmakis, E. et

al. Attosecond control and measurement: lightwave electronics. _Science_ 317, 769–775 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Wörner, H. J. High-harmonic spectroscopy: from

femtosecond to attosecond molecular dynamics. _CHIMIA Int. J. Chem._ 65, 299–302 (2011). Article  CAS  Google Scholar  * Reiss, H. R. Complete Keldysh theory and its limiting cases. _Phys.

Rev. A_ 42, 1476–1486 (1990). Article  ADS  CAS  PubMed  Google Scholar  * Vampa, G. et al. Linking high harmonics from gases and solids. _Nature_ 522, 462–464 (2015). Article  ADS  CAS 

PubMed  Google Scholar  * Wu, M., Ghimire, S., Reis, D. A., Schafer, K. J. & Gaarde, M. B. High-harmonic generation from Bloch electrons in solids. _Phys. Rev. A_ 91, 043839 (2015).

Article  ADS  CAS  Google Scholar  * Luu, T. T. et al. Extreme ultraviolet high-harmonic spectroscopy of solids. _Nature_ 521, 498–502 (2015). Article  ADS  CAS  PubMed  Google Scholar  *

You, Y. S. et al. High-harmonic generation in amorphous solids. _Nat. Commun._ 8, 724 (2017). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Schubert, O. et al. Sub-cycle

control of terahertz high-harmonic generation by dynamical Bloch oscillations. _Nat. Photonics_ 8, 119–123 (2014). Article  ADS  CAS  Google Scholar  * Hohenleutner, M. et al. Real-time

observation of interfering crystal electrons in high-harmonic generation. _Nature_ 523, 572–575 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Vampa, G., You, Y. S., Liu, H., Ghimire,

S. & Reis, D. A. Observation of backward high-harmonic emission from solids. _Opt. Express_ 26, 12210 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Lu, J., Cunningham, E. F., You,

Y. S., Reis, D. A. & Ghimire, S. Interferometry of dipole phase in high harmonics from solids. _Nat. Photonics_ 13, 96–100 (2019). Article  ADS  CAS  Google Scholar  * Lewenstein, M.,

Salières, P. & L’Huillier, A. Phase of the atomic polarization in high-order harmonic generation. _Phys. Rev. A_ 52, 4747–4754 (1995). Article  ADS  CAS  PubMed  Google Scholar  * Han,

S. et al. High-harmonic generation by field enhanced femtosecond pulses in metal-sapphire nanostructure. _Nat. Commun._ 7, 13105 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google

Scholar  * Yang, Y. et al. High-harmonic generation from an epsilon-near-zero material. _Nat. Phys._ 15, 1022–1026 (2019). Article  CAS  Google Scholar  * Sivis, M. et al. Tailored

semiconductors for high-harmonic optoelectronics. _Science_ 357, 303–306 (2017). Article  ADS  CAS  PubMed  Google Scholar  * You, Y. S., Lu, J., Cunningham, E., Roedel, C. & Ghimire, S.

Crystal orientation-dependent polarization state of high-order harmonics. _Opt. Lett._ 44, 530 (2018). Article  ADS  Google Scholar  * Luu, T. T. & Wörner, H. J. Measurement of the

Berry curvature of solids using high-harmonic spectroscopy. _Nat. Commun._ 9, 916 (2018). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Saito, N. et al. Observation of

selection rules for circularly polarized fields in high-harmonic generation from a crystalline solid. _Optica_ 4, 1333 (2017). Article  ADS  CAS  Google Scholar  * Liu, H. et al. Overcoming

the absorption limit in high-harmonic generation from crystals. Preprint at https://ui.adsabs.harvard.edu/abs/2019arXiv190502821L (2019). * Park, H. et al. High-order harmonic generations in

intense MIR fields by cascade three-wave mixing in a fractal-poled LiNbO3 photonic crystal. _Opt. Lett._ 42, 4020 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Liu, H. et al.

Enhanced high-harmonic generation from an all-dielectric metasurface. _Nat. Phys._ 14, 1006–1010 (2018). Article  CAS  Google Scholar  * Silva, R. E. F., Blinov, I. V., Rubtsov, A. N.,

Smirnova, O. & Ivanov, M. High-harmonic spectroscopy of ultrafast many-body dynamics in strongly correlated systems. _Nat. Photonics_ 12, 266–270 (2018). Article  ADS  CAS  Google

Scholar  * Bauer, D. & Hansen, K. K. High-harmonic generation in solids with and without topological edge states. _Phys. Rev. Lett._ 120, 177401 (2018). Article  ADS  CAS  PubMed  Google

Scholar  * Chacón, A. et al. Observing topological phase transitions with high harmonic generation. Preprint at https://ui.adsabs.harvard.edu/abs/2018arXiv180701616C (2018). * Silva, R. E.

F., Jiménez-Galán, Á., Amorim, B., Smirnova, O. & Ivanov, M. Topological strong-field physics on sub-laser-cycle timescale. _Nat. Photonics_ 13, 849–854 (2019). Article  ADS  CAS  Google

Scholar  * Tancogne-Dejean, N., Sentef, M. A. & Rubio, A. Ultrafast modification of Hubbard U in a strongly correlated material: Ab initio high-harmonic generation in NiO. _Phys. Rev.

Lett._ 121, 097402 (2018). Article  ADS  PubMed  Google Scholar  * Sobota, J. A. et al. Ultrafast optical excitation of a persistent surface-state population in the topological insulator

Bi2Se3. _Phys. Rev. Lett._ 108, 117403 (2012). Article  ADS  CAS  PubMed  Google Scholar  * Glownia, J. M. et al. Time-resolved pump-probe experiments at the LCLS. _Opt. Express_ 18,

17620–17630 (2010). Article  ADS  CAS  PubMed  Google Scholar  * Navarrete, F., Ciappina, M. F. & Thumm, U. Crystal-momentum-resolved contributions to high-order harmonic generation in

solids. _Phys. Rev. A_ 100, 033405 (2019). Article  ADS  CAS  Google Scholar  * Golde, D., Meier, T. & Koch, S. W. High harmonics generated in semiconductor nanostructures by the coupled

dynamics of optical inter- and intraband excitations. _Phys. Rev. B_ 77, 075330 (2008). Article  ADS  CAS  Google Scholar  * Tancogne-Dejean, N., Mücke, O. D., Kärtner, F. X. & Rubio,

A. Impact of the electronic band structure in high-harmonic generation spectra of solids. _Phys. Rev. Lett._ 118, 087403 (2017). Article  ADS  PubMed  Google Scholar  * Saule, T. et al.

High-flux ultrafast extreme-ultraviolet photoemission spectroscopy at 18.4 MHz pulse repetition rate. _Nat. Commun._ 10, 458 (2019). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar

  * Rana, A. et al. Ptychographic coherent diffractive imaging for attosecond pulses. Preprint at https://ui.adsabs.harvard.edu/abs/2019arXiv190700411R (2019). * Kaplan, C. J. et al.

Femtosecond tracking of carrier relaxation in germanium with extreme ultraviolet transient reflectivity. _Phys. Rev. B_ 97, 205202 (2018). Article  ADS  CAS  Google Scholar  * Geneaux, R.,

Marroux, H. J., Guggenmos, A., Neumark, D. M. & Leone, S. R. Transient absorption spectroscopy using high harmonic generation: a review of ultrafast X-ray dynamics in molecules and

solids. _Philos. Trans. R. Soc. A_ 377, 20170463 (2019). Article  ADS  CAS  Google Scholar  * Buss, J. H. et al. A setup for extreme-ultraviolet ultrafast angle-resolved photoelectron

spectroscopy at 50-kHz repetition rate. _Rev. Sci. Instrum._ 90, 023105 (2019). Article  ADS  PubMed  CAS  Google Scholar  * Dörner, R. et al. Cold target recoil ion momentum spectroscopy: a

‘momentum microscope’to view atomic collision dynamics. _Phys. Rep._ 330, 95–192 (2000). Article  ADS  Google Scholar  * Chang, Z. Enhancing keV high harmonic signals generated by long-wave

infrared lasers. _OSA Contin._ 2, 2131–2136 (2019). Article  CAS  Google Scholar  * Hartmann, N. et al. Attosecond time–energy structure of X-ray free-electron laser pulses. _Nat.

Photonics_ 12, 215–220 (2018). Article  ADS  CAS  Google Scholar  * Duris, J. et al. Tunable isolated attosecond X-ray pulses with gigawatt peak power from a free-electron laser. _Nat.

Photonics_ 14, 30–36 (2020). Article  CAS  Google Scholar  * Sansone, G. et al. Isolated single-cycle attosecond pulses. _Science_ 314, 443–446 (2006). Article  ADS  CAS  PubMed  Google

Scholar  * Goulielmakis, E. et al. Single-cycle nonlinear optics. _Science_ 320, 1614–1617 (2008). Article  ADS  CAS  PubMed  Google Scholar  * Ferrari, F. et al. High-energy isolated

attosecond pulses generated by above-saturation few-cycle fields. _Nat. Photonics_ 4, 875 (2010). Article  ADS  CAS  Google Scholar  * Zhao, K. et al. Tailoring a 67 attosecond pulse through

advantageous phase-mismatch. _Opt. Lett._ 37, 3891–3893 (2012). Article  ADS  PubMed  Google Scholar  * Kim, K. T. et al. Photonic streaking of attosecond pulse trains. _Nat. Photonics_ 7,

651–656 (2013). Article  ADS  CAS  Google Scholar  * Takahashi, E. J., Lan, P., Mücke, O. D., Nabekawa, Y. & Midorikawa, K. Attosecond nonlinear optics using gigawatt-scale isolated

attosecond pulses. _Nat. Commun._ 4, 2691 (2013). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar  * Gaumnitz, T. et al. Streaking of 43-attosecond soft-X-ray pulses generated by a

passively CEP-stable mid-infrared driver. _Opt. Express_ 25, 27506–27518 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Cousin, S. L. et al. High-flux table-top soft x-ray source

driven by sub-2-cycle, CEP stable, 1.85 micron, 1-kHz pulses for carbon K-edge spectroscopy. _Opt. Lett._ 39, 5383–5386 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Shan, B. &

Chang, Z. Dramatic extension of the high-order harmonic cutoff by using a long-wavelength driving field. _Phys. Rev. A_ 65, 011804 (2001). Article  ADS  CAS  Google Scholar  * Popmintchev,

T. et al. Bright coherent ultrahigh harmonics in the keV X-ray regime from mid-infrared femtosecond lasers. _Science_ 336, 1287–1291 (2012). Article  ADS  MathSciNet  CAS  PubMed  Google

Scholar  * Altucci, C. et al. Influence of atomic density in high-order harmonic generation. _J. Opt. Soc. Am. B_ 13, 148–156 (1996). Article  ADS  CAS  Google Scholar  * Johnson, A. S. et

al. High-flux soft x-ray harmonic generation from ionization-shaped few-cycle laser pulses. _Sci. Adv._ 4, eaar3761 (2018). Article  ADS  PubMed  PubMed Central  CAS  Google Scholar 

Download references ACKNOWLEDGEMENTS This work was supported by United States Air Force Office of Scientific Research (AFOSR) (FA9550-15-1-0037, FA9550-16-1-0013, FA9550-17-1-0099); Army

Research Office (ARO) (W911NF-14-1-0383, W911NF-19-1-0224); Defense Advanced Research Projects Agency (DARPA) (D18AC00011); Defense Threat Reduction Agency (HDTRA11910026); National Science

Foundation (1806575); Department of Energy; Office of Science; Basic Energy Sciences; Chemical Sciences; Geosciences and Biosciences Division through the Early Career Research Program and

Chinese Academy of Science Pioneer Hundred Talents Program (2018-131-S). AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing,

100094, China Jie Li * Institute for the Frontier of Attosecond Science and Technology, CREOL and Department of Physics, University of Central Florida, Orlando, FL, 32816, USA Jie Li, Andrew

Chew, Seunghwoi Han, Jialin Li, Yi Wu & Zenghu Chang * School of Optoelectronics, University of the Chinese Academy of Sciences, Beijing, 100049, China Jie Li * Stanford PULSE

Institute, SLAC National Accelerator Laboratory, Menlo Park, CA, 94025, USA Jian Lu & Shambhu Ghimire * School of Mechanical Engineering, Chonnam National University, Gwangju, 61186,

Republic of Korea Seunghwoi Han * Department of Physics, University of Miami, Coral Gables, FL, 33146, USA He Wang Authors * Jie Li View author publications You can also search for this

author inPubMed Google Scholar * Jian Lu View author publications You can also search for this author inPubMed Google Scholar * Andrew Chew View author publications You can also search for

this author inPubMed Google Scholar * Seunghwoi Han View author publications You can also search for this author inPubMed Google Scholar * Jialin Li View author publications You can also

search for this author inPubMed Google Scholar * Yi Wu View author publications You can also search for this author inPubMed Google Scholar * He Wang View author publications You can also

search for this author inPubMed Google Scholar * Shambhu Ghimire View author publications You can also search for this author inPubMed Google Scholar * Zenghu Chang View author publications

You can also search for this author inPubMed Google Scholar CONTRIBUTIONS Jie Li, A.C., S.H., Jialin Li, Y.W., H.W., and Z.C. drafted the sections of generation and applications of gas-phase

soft X-ray HHG. Jian Lu and S.G. drafted the solid-state HHG with corresponding applications. All authors planned and contributed to the final version of the paper. CORRESPONDING AUTHOR

Correspondence to Zenghu Chang. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature remains neutral

with regard to jurisdictional claims in published maps and institutional affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0

International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the

source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative

Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by

statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit

http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Li, J., Lu, J., Chew, A. _et al._ Attosecond science based on high harmonic

generation from gases and solids. _Nat Commun_ 11, 2748 (2020). https://doi.org/10.1038/s41467-020-16480-6 Download citation * Received: 21 December 2018 * Accepted: 05 May 2020 * Published:

02 June 2020 * DOI: https://doi.org/10.1038/s41467-020-16480-6 SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a

shareable link is not currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative