Reader TTS

ABSTRACT Symmetry plays an important role in determining the physical properties in condensed matter physics, as the symmetry operations of any physical property must include the symmetry

operations of the point group of the crystal. As a consequence, crystallographic polarity and chirality are expected to have an impact on the Cooper pairing in a superconductor. While

superconductivity with crystallographic polarity and chirality have both been found in a few crystalline phases separately; however, their coexistence and material realizations have not been

studied. Here, by utilizing transport, Raman scattering, and transmission electron microscopy, we unveil a unique realization of superconductivity in single-crystalline Mo3Al2C

(superconducting _T_c=8 K) with a polar charge-density-wave phase and well-defined crystallographic chirality. We show that the intriguing charge density wave order leads to a

noncentrosymmetric-nonpolar to polar transition below _T_*=155K via breaking both the translational and rotational symmetries. Superconductivity emerges in this polar and chiral crystal

structure below _T_c=8 K. Our results establish that Mo3Al2C is a superconductor with crystallographic polarity and chirality simultaneously, and motivate future studies of unconventional

superconductivity in this category. SIMILAR CONTENT BEING VIEWED BY OTHERS ENGINEERING PHASE COMPETITION BETWEEN STRIPE ORDER AND SUPERCONDUCTIVITY IN LA1.88SR0.12CUO4 Article Open access 10

July 2024 SUPERCONDUCTIVITY ENHANCEMENT IN POLAR METAL REGIONS OF SR0.95BA0.05TIO3 AND SR0.985CA0.015TIO3 REVEALED BY SYSTEMATIC NB DOPING Article Open access 30 November 2022 TUNING OF

CHARGE ORDER BY UNIAXIAL STRESS IN A CUPRATE SUPERCONDUCTOR Article Open access 10 August 2024 INTRODUCTION The concept of ‘ferroelectric metals’ was first proposed by Anderson and Blount

more than half a century ago1. Ferroelectricity and metallicity are conventionally considered incompatible as itinerant electrons tend to screen long-range Coulomb interactions and weaken

polar instabilities. This makes the appearance of an inversion-symmetry breaking transition in metals rare, although numerous compounds are predicted to host such transitions2,3,4,5,6,7.

Despite these challenges, LiOsO3 and WTe2/MoTe2 are two unambiguous examples of experimentally verified polar metals, driven by polar instability which is decoupled with itinerant electrons

at the Fermi level8,9,10 and in-plane interlayer sliding mechanisms11,12, respectively. Another way to generate polarization is via translational symmetry breaking by virtue of a

charge-density wave (CDW). When a non-centrosymmetric charge modulation occurs, it could result in a potential net electric polarization13,14,15. Achieving CDW-driven polar metals have

particular significance that they can in principle enable ultrafast switching at characteristic electronic rather than lattice time scales16,17. Since superconductivity (SC) tends to arise

from itinerant electrons in a metallic system, the coexistence of ferroelectricity/polarity and SC is unusual and is a topic of active discussions18,19,20,21. Examples of such polar

superconductors (existence of a polar axis in a superconductor) are the doped SrTiO3 (_T_c less than 1 K)18,19,20, bilayer Td-MoTe2 (_T_c = 2.3 K)21, and various heavy fermions

superconductors (_T_c ~ 1–3 K)22. The presence of a polar axis in a superconductor gives rise to phenomena such as exotic nonreciprocal charge transport23,24,25,26, including the

superconducting diode effect27, the mixing of spin-triplet and spin-singlet order parameters, as well as topological SC featuring a Majorana edge state28. On the other hand, superconductors

with a chiral structure are reported in Li2Pd3B, Li2Pt3B29,30, Mo3Al2C31, NbRh2B232, and TaRh2B232. Among them, Li2Pt3B has been proposed to be a candidate for chiral SC29. Superconductors

with a polar and chiral crystal structure are expected to have unconventional Cooper paring, as the superconducting order parameter must respect the symmetry of the underlying crystal

lattice according to the Neumann’s principle. However, such type of superconductors is rare. Identifying superconductors in this category are important not only for fundamental science in

the multiferroic and SC community, but also for technological applications27. In this work, we present evidence for a new category of superconductor, Mo3Al2C, which exhibits superconducting

transition temperature (_T_c) of 8 K and possesses both structural polarity and chirality. The polarization is induced by a CDW order that appears below _T_* = 155 K, characterized by a

cubic-nonpolar to rhombohedral-polar phase transition. SC emerges deep within this polar and chiral crystal structure below _T_c, establishing Mo3Al2C as a unique superconductor with both

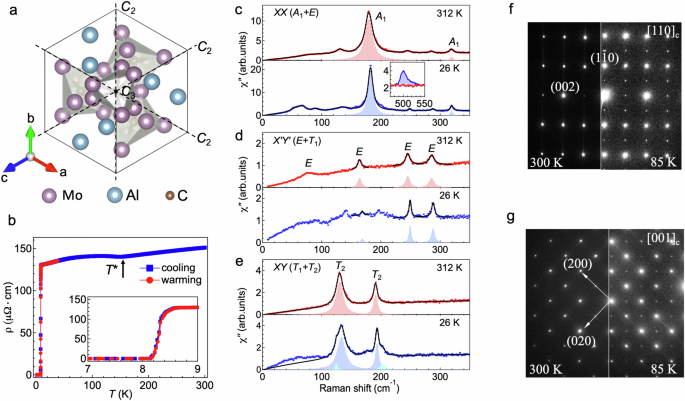
structural polarity and chirality. RESULTS CRYSTAL STRUCTURE Mo3Al2C has a cubic structure with space group _P_4132 or its enantiomorphic space group _P_4332 (point group _O_) at room

temperature (Supplementary Note I). The crystal structure lacks inversion and mirror symmetries. There are four three-fold axes along the body-diagonal directions and three _C_2 axes

perpendicular to a fixed three-fold axis as shown in Fig. 1a. Thus, the structure of Mo3Al2C is noncentrosymmetric, chiral, and nonpolar at room temperature. Upon cooling, as shown in Fig. 

1b, resistivity measurement shows that there is a superconducting transition at around _T_c = 8 K and bulk SC is confirmed by the magnetic susceptibility measurement (Supplementary Note I).

The resistivity measurement also shows a dip at around _T_ * = 155 K33. The anomalies at _T_ * are also found in earlier magnetic susceptibility, specific heat, nuclear-magnetic-resonance

(NMR) measurements34,35. To understand the resistivity anomaly at _T_ *, we perform Raman scattering measurement from a polished (1 0 0) surface of Mo3Al2C in the _X__X_, \({X}^{{\prime}

}{Y}^{{\prime} }\), and _X__Y_ scattering geometries at 312 K and 26 K. For the _X__X_ scattering geometry shown in Fig. 1c, we detect two phonon modes at 180 and 319 cm−1 with Lorentzian

lineshape at 312 K and 26 K, and a third phonon mode at around 500 cm−1 that appears only at low temperature. These three _A_1-symmetry modes are dominated by Mo, Al, and C lattice

vibrations, respectively36 (Supplementary Note II). Specifically, the broad peak at around 50 cm−1 appearing at low temperatures is the amplitude mode of the CDW order parameter (see the

section of the CDW transition). The peak at 129 cm−1 at 312 K in the _X__X_ scattering geometry is a leakage of the _T_2 phonon from the _X__Y_ scattering geometry due to imperfect cutting

or sample polishing of the single crystal. In the \({X}^{{\prime} }{Y}^{{\prime} }\) scattering geometry, we detect three sharp phonon modes at 164, 245, and 285 cm−1 and a broad mode at 75 

cm−1 at 312 K shown in Fig. 1d. They are all _E_-symmetry phonon modes. The three sharp _E_ modes are first-order phonons, while the broad one is a second-order two-phonon excitation as the

linewidth is four times of the three sharp ones. Below _T_ *, the three first-order _E_-symmetry phonon modes do not split at 26 K. In the _X__Y_ scattering geometry, we detect two

_T_2-symmetry phonons at 129 and 190 cm−1 at 312 K. They split into two modes in the 26 K data as shown in Fig. 1e, indicating a structural phase transition below _T_ *. Since the _T_2

phonon splitting is independent of the domain orientations, the presence of domains does not affect the conclusion. By virtue of the correlation table of the point group _O_ of the

high-temperature structure (METHODS), based on the fact that _E_ modes do not split while _T_2 modes split into two modes below _T_ *, we infer that low-temperature structure belongs to a

rhombohedral point group _C_3 or _D_3. To reveal the potential ordering vector of the low-temperature structure, we conduct transmission electron microscopy (TEM) measurement on Mo3Al2C.

Figure 1f, g represent the [1 1 0]c and [0 0 1]c zone-axis selected area electron diffraction patterns taken at 300 K and 85 K, respectively. The data at 300 K [left panels of Fig. 1f, g]

are consistent with the primitive _P_4132 cubic structure (_a_ = 6.8638 Å). The data at 85 K, shown in the right panels of Fig. 1f, g, reveal evidence of a phase transition from the presence

of the systematic superlattice Bragg peaks alongside the fundamental Bragg peaks. The appearance of the superlattice reflections (1/2, −1/2, 0) [Fig. 1f] and (1/2, −1/2, 0)/(−1/2, −1/2, 0)

[Fig. 1g] while they are absent at half of (0, 0, 1) indicates a transition involving 2 × 2 × 1 supercell in the hexagonal setting. Our results suggest that Mo3Al2C undergoes a transition to

a rhombohedral structure below _T_ *, leading to either the nonpolar R32 (point group _D_3) or the polar R3 (point group _C_3) space group with lattice vectors (−2, 2, 0), (0, −2, 2), and

(1, 1, 1) in relation to those of the cubic unit cell. The lattice constants for the supercell are _a_ ≈ 11.896 Å, _α_ = 109.58∘ in the trigonal setting or _a_ ≈ 19.44 Å, _c_ ≈ 11.83 Å in

the hexagonal setting. POLAR DOMAINS An intriguing question arises: Is the superconductor Mo3Al2C with structural chirality also a polar superconductor? To address this question and probe

polar domains in Mo3Al2C, we utilize dark-field transmission electron microscopy (DF-TEM), which is known for its high spatial resolution and ability to isolate distinct types of domains

using a specific diffraction spots37. In Fig. 2, we show a series of DF-TEM images taken along the [1 1 0]c or [1 \(\bar{1}\)\(\bar{4}\)]h direction using superlattice peaks (1)

\({g}_{1}^{\pm }=\pm {(1/2,-1/2,4)}_{{{{\rm{c}}}}}\) containing the polar contributions along the [1 1 1]c polar axis [Fig. 2a, b], and (2) \({g}_{2}^{\pm }=\pm

{(1/2,-1/2,0)}_{{{{\rm{c}}}}}\) containing mainly the information in the plane perpendicular to the [1 1 1]c polar axis [Fig. 2c]. Evident in Fig. 2a, b is the presence of 180∘-type polar

domains on a 100-nm scale, showing broken fourfold and two-fold symmetry of the cubic phase, resulting in the polar R3 phase with point group _C_3. The polar domains with black and white

contrasts are associated with the  ±[1 1 1]c or  ±[001]h polar axes, ~35∘ away from the out-of-plane direction of the images. In addition to the small polar domains, sub-micrometer-sized

wavey antiphase boundaries shown as dark lines are resolved [Fig. 2c]. These antiphase boundaries do not exist above _T_ * and exhibit varying features during different cooling cycles,

suggesting that domain formation below _T_ * is not simply due to pinning by disorder such as chemical defects or dislocations (Supplementary Note III). These images show that there seems to

be no clear interlockings for these two types of domains below _T_ *. Our results reveal a non-polar to polar transition below _T_ * in the superconductor Mo3Al2C. CDW TRANSITION To further

uncover the nature of phase transition at _T_ *, we study the temperature dependence of the Raman response in the _X__X_ and \({X}^{{\prime} }{Y}^{{\prime} }\) scattering geometries. In

Fig. 3a, b, we show the Raman response in the _X__X_ scattering geometry. Upon cooling to _T_ *, the low-energy electronic continuum below 100 cm−1 builds up gradually in the _X__X_ (_A_1 + 

_E_) scattering geometry while the continuum remains unchanged for the \({X}^{{\prime} }{Y}^{{\prime} }\) (_E_ + _T_1) scattering geometry (Supplementary Note IV), indicating the existence

of the _A_1-type fully-symmetric charge fluctuations. This is a signature of a precursor density-wave order approaching _T_ *, similar to the CDW-compound ErTe338. Below _T_ * as shown in

Fig. 3c, the most prominent feature is the redistribution of the low-energy spectra weight: The low-energy continuum intensity below 40 cm−1 is progressively suppressed, while the

high-energy continuum intensity in the range between 40 cm−1 and 250 cm−1 is enhanced and a broad peak centered at around 60 cm−1 (labeled as _A_1) is developed. Such a spectra weight

transfer is an evidence for gap opening below _T_ *39. This observation is consistent with gap opening from the previous 27Al NMR studies that the Knight shift and the spin-lattice

relaxation rates are significantly reduced below _T_ *35,40. Therefore, the existence of charge fluctuations above _T_ *, the gap opening below _T_ *, and superlattice Bragg peaks appearance

below _T_ * all point to a second-order CDW transition at _T_ *. Moreover, as the temperature cools below 100 K, two shoulder peaks at around 68 (labeled as _A_2) and 90 cm−1 (labeled as

_A_3) become noticeable and gain intensity on top of the _A_1 peak. In Fig. 3d, e, we show the Raman response in the \({X}^{{\prime} }{Y}^{{\prime} }\)(_E_ + _T_1) scattering geometry. In

addition to the three fundamental _E_ modes at 164, 245, and 285 cm−1 which persists upon cooling from 312 K to 26 K, several new _E_-symmetry modes between 140 cm−1 and 220 cm−1 appear

below _T_ *. Notably, the two-phonon excitation feature (labeled as _E_1) softens a bit upon cooling to _T_ *. In Fig. 3f–h, we present the temperature dependence of the mode energy,

half-width-at-half maximum (HWHM), and the integrated area for the _A_1, _A_2, _A_3, and _E_1 modes. The _A_1 mode frequency increases from 48 to 60 cm−1 while _A_2 and _A_3 modes barely

change upon cooling below _T_ *. In contrast, the _E_1 mode softens from 75 cm−1 at 312 K to 70 cm−1 at _T_ *. The HWHM for the _A_1 mode decreases by a factor of three, while _A_2 and _A_3

modes barely change upon cooling. The integrated area for the _A_1 mode increases gradually below _T_ *, reaching four times of its value at _T_ * when cooled to the lowest temperature,

while the _A_2 and _A_3 modes’ integrated area increase moderately below _T_ *. The differences in the temperature dependence between _A_1, _A_2, and _A_3 peaks suggest that the _A_1 peak

represents the CDW amplitude mode while _A_2 and _A_3 peaks correspond to the folded phonon modes41,42. Upon cooling below _T_c, the phononic features barely change, namely, the amplitude

mode _A_1 and folded phonon modes _A_2 and _A_3 remain the same (Supplementary Note V). This indicates that the CDW order coexists with SC. Furthermore, since Raman scattering is

exceptionally sensitive to the subtle breaking of crystalline symmetry39,43, the persistence of the same phononic features above and below _T_c indicates that the point group symmetry (_C_3)

persists also in the SC state. Thus, the SC state of Mo3Al2C is both chiral and polar. DISCUSSIONS ORIGIN OF THE CDW TRANSITION We now discuss the origin of the CDW transition at _T_ * in

Mo3Al2C. Based on the density functional theory (DFT) calculations (Supplementary Note VI), there are three unstable modes in the phonon dispersion for the cubic phase of Mo3Al2C: _Γ_4(0, 0,

0), _M_5(0.5, 0.5, 0), and _X_2(0.5, 0.5, 0), consistent with ref. 36. The _Γ_4 instability leads to a R3 structure without translational-symmetry breaking, and hence the same unit-cell

volume. The only structure with 3-fold rotational symmetry that the _X_2 instability can lead to is a 2 × 2 × 2 supercell with eight times the volume of the primitive cell (Supplementary

Note VII). On the other hand, the _M_5 instability can lead to the R3 structure with the correct translational symmetry breaking and 4 times the volume of the primitive cell. Thus, the only

way to get a CDW structure below _T_ * commensurate with 2 × 2 × 1 supercell in the hexagonal setting and 3-fold rotational symmetry in the R3 phase is to have a _M_5 lattice instability at

the Brillouin zone boundary. The observed softening of the second-order _E_1 mode above _T_ * [Fig. 3f] suggests the softening phonon branch at around _M_ points, similar to the study of

2H-NbSe241. ORIGIN OF THE POLARIZATION The origin of the polarization in Mo3Al2C poses new questions. Since the crystal structure is already noncentrosymmetric above _T_ *, the transition to

the polar structure is not a simple off-centering of atoms, but rather roots in the breaking of the two-fold rotational symmetries perpendicular to the polar axis in the symmetry group of

the re-arranged atoms below _T_ * [Fig. 1a]. It can nevertheless be either due to a zone-center instability that breaks the symmetry (proper ferroelectricity), or a zone-boundary instability

that breaks translational symmetry in addition to the rotational symmetry (improper ferroelectricity). In the former case, another important question arises about whether the transition is

a displacive or an order-disorder type transition. The order-disorder mechanism was discussed for the case of LiOsO344,45. One of the key evidence in support of this mechanism in LiOsO3 is

the sharp drop in resistivity below the polar transition. The large resistivity above the transition is attributed to the incoherent charge transport induced by the disordered Li off-center

displacements8. For Mo3Al2C, this mechanism for the nonpolar-to-polar transition is less likely, because the temperature dependence of the resistivity is almost flat from 300 K down to 8 K

for single crystals [Fig. 1b]33 as well as polycrystalline samples46. While some amount of disorders or vacancies could be present in the Mo3Al2C sample33, the flat resistivity curve

suggests that the scattering rates for the electrons barely change upon cooling through the transition, which rules out disorders near the transition, and hence an order-disorder mechanism.

Our DFT lattice dynamics calculations, as well as earlier report36, indicate that there are both zone-center and zone-boundary instabilities, which makes both proper and improper

instabilities possible. The unstable _Γ_ mode transforms as the _Γ_4 irreducible representation. It is infrared-active and a polar instability. Thus, the zone-center _Γ_4 mode leading to the

polarization while a zone-boundary _M_5 mode leading to the CDW order is seemingly possible. However, this scenario is inconsistent with the observation that there is only a single

transition at _T_ *. It is also not possible for the CDW order being a secondary and improper order parameter that condenses only due to the nonzero amplitude of the polar mode, because the

CDW order breaks the translational symmetry, which by definition cannot be broken by a zone-center _Γ_ polar mode. This may lead us to conclude that the polarization is induced by an

improper mechanism, where a zone-boundary _M_5 mode couples with a zone-center _Γ_4 polar mode, and leads to a nonzero magnitude of the polarization below _T_ *. The details of this coupling

can be understood by building a Landau free-energy expansion for the high-temperature cubic structure via the trilinear coupling between the _M_5 and the polarization P along the [1 1 1]

pseudo-cubic direction (Supplementary Note VIII). When the _M_5 mode condenses, this leads to a first-order term in P to appear in the free energy expansion, which necessarily leads to a

nonzero value of P (Supplementary Note VIII). We note that the density of states at the Fermi level are dominated by Mo 4_d_ electronic states from the DFT band structure calculations31. In

contrast, the Al and C electronic states are negligibly small between −2 eV and 2 eV, and they get a bit larger below −2 eV31. Furthermore, from the DFT phonon calculations36, the phonon

density of states below 100 cm−1 are dominated by Mo lattice vibration modes, while they are dominated by C lattice vibration modes above 500 cm−1. In between 100 cm−1 and 500 cm−1, they are

dominated by Mo and Al lattice vibration modes. In the Raman spectra shown in Fig. 1c–e, we detect substantial mode intensity for the new Mo modes (_A_1, _A_2, and _A_3) below 100 cm−1 and

new C modes at around 500 cm−1 in the _X__X_ scattering geometry, while those new _E_-symmetry modes involving the Al lattice vibration in-between 100 cm−1 and 350 cm−1 in the

\({X}^{{\prime} }{Y}^{{\prime} }\) scattering geometry are five times weaker. This indicates that Mo and C atoms are mainly involved in the polar distortions below _T_ *. We note that

previous 27Al NMR studies revealed the broadening of Al spectrum below _T_ * and associated it to the gradual distortions near the Al sites toward a lower symmetric structure40. To resolve

the lattice distortions below _T_ *, we have performed the single-crystal X-ray diffraction measurement of Mo3Al2C at 300 K and 100 K. We failed to detect the superlattice Bragg peaks in the

diffraction patterns (Supplementary Note X). Regardless of the origin for the polarization below _T_ *–proper or improper mechanism, substantial C-lattice contributions to the polar

distortion, which are decoupled from the itinerant Mo 4_d_ electronic states around the Fermi level, help to stabilize the polar metal phase of Mo3Al2C according to the decoupled electron

mechanism2,9,10 SC STATE Finally, we discuss the symmetry and the properties of the SC state in Mo3Al2C. The point group symmetry of Mo3Al2C in the SC state is _C_3. It contains two

irreducible representations _A_ and _E_. The _A_-symmetry SC order parameter preserves the three-fold rotational symmetry and the SC gap could be isotropic or anisotropic. The _E_-symmetry

SC order parameter breaks the three-fold rotational symmetry and is a two-component order parameter. The lack of inversion symmetry in the low-crystallographic-symmetry Mo3Al2C necessarily

leads to the mixing of singlet and triplet SC order parameters, thus creating an unconventional SC state. Previous studies have reported that Mo3Al2C has a _s_-wave-like nodeless

gap33,34,46,47. However, a recent muon spin relaxation/rotation (_μ_SR) study revealed that the ratio \({T}_{c}/{\lambda }_{{{{\rm{eff}}}}}^{-2}\) (_λ_eff is the effective London penetration

depth) is comparable to the class of unconventional superconductors in the Uemura plot, which points towards an unconventional pairing mechanism in the isostructural compound W3Al2C48. The

study of the relationship between the polar structure and the symmetry of the superconducting order parameters in Mo3Al2C is beyond the scope of this current work but will motivate future

studies. In summary, we identify Mo3Al2C as a new category of superconductor with structural polarity and chirality. Our results open up an avenue to discover more CDW-driven polarization in

noncentrosymmetric metals as well as polar superconductors. Materials in this category could have new physical properties and applications, motivating future studies of switchable

ferroelectric SC21, nonreciprocal charge transport24,27, and unconventional paring mechanism28,49. METHODS SINGLE CRYSTAL PREPARATION AND CHARACTERIZATION Mo3Al2C single crystals were grown

using a slow cooling method in a sealed alumina tube. Powders of Mo : Al : C in molar ratio 3 : 4 : 1 were mixed and pre-reacted in a sealed vacuum quartz tube at 1000 °C for 5 h. The

product was filled into an one-end-closed alumina tube. Then, the open end was sealed in a laser floating zone furnace in an Argon flow. The sealed alumina tube was heated to 1650 °C, kept

for 5 h, 5 °C/h cooled to 1250 °C, then 100 °C/h cooled to room temperature. Millimeter size crystals are mechanically separated from the product, and the single-crystallinity is confirmed

by X-ray Laue diffraction and polarized light optical microscope observation. Electric transport measurements were carried out in a standard four-point probe method in the (1 0 0) plane in

the He exchange gas environment using a PPMS on both cooling-down and warming-up processes. Magnetic susceptibility measurements were carried out in a Quantum Design SQUID magnetometer in He

exchange gas environment in zero-field cooled (ZFC) and field-cooled (FC) processes. The crystal structure was determined using a Bruker single crystal x-ray diffractometer. The structure

was refined using the SHELXTL Software Package. Additionally, we have performed Laue diffraction to orientate Mo3Al2C crystals before the sample polishing. POLARIZATION-RESOLVED RAMAN

SPECTROSCOPY The nature exposed surface of Mo3Al2C is (1 1 0) crystallographic plane. To decompose the Raman signal into separate irreducible representations, we choose to work with the high

symmetry (1 0 0) crystallographic plane. The as-grown sample is polished to expose its (1 0 0) crystallographic plane with a lapping film (1 μm, Buehler). A strain-free area for Raman

scattering measurement is examined by a Nomarski image. The strain-free area is further examined by comparing the phonon linewidth obtained on the as-grown (1 1 0) crystallographic plane and

the polished (1 0 0) crystallographic plane. We did not find any noticeable polishing-induced linewidth broadening. The polished crystals with (1 0 0) plane used for the Raman scattering

study were positioned in a continuous helium flow optical cryostat. The Raman measurements were mainly performed using the Kr+ laser line at 647.1 nm (1.92 eV) in a quasibackscattering

geometry along the crystallographic _c_ axis. The excitation laser beam was focused into a 50 × 100 μm2 spot on the _a__b_ plane, with the incident power around 12 mW. For the measurement

below _T__c_, an elongated laser spot (50 × 600 μm2) and a weak laser power 1–2 mW is used to reduce laser heating. The scattered light was collected and analyzed by a triple-stage Raman

spectrometer and recorded using a liquid nitrogen-cooled charge-coupled detector. Linear and circular polarizations are used in this study to decompose the Raman data into different

irreducible representations. The instrumental resolution was maintained better than 1.5 cm−1. All linewidth data presented in this paper have been corrected for the instrumental resolution

by fitting the Raman peaks using a Voigt profile. The temperature shown in this paper has been corrected for laser heating (Supplementary Sec. XI). All spectra shown were corrected for the

spectral response of the spectrometer and charge-coupled detector. The obtained Raman intensity _I__μ__v_, which is related to the Raman response \({\chi }^{{\prime\prime} }(\omega,T)\):

\({I}_{\mu v}(\omega,T)=[1+n(\omega,T)] \, {\chi }_{\mu \nu }^{{\prime\prime} }(\omega,T)\). Here _μ_(_v_) denotes the polarization of the incident (scattered) photon, _ω_ is energy, _T_ is

temperature, and _n_(_ω_, _T_) is the Bose factor. The Raman spectra have been recorded from the _a__b_ (1 0 0) surface for scattering geometries denoted as \(\mu v=XX,XY,{X}^{{\prime}

}{X}^{{\prime} },{X}^{{\prime} }{Y}^{{\prime} },RR,RL\), which is short for _Z_(_μ__v_)_Z_ in Porto’s notation, where _X_ and _Y_ denotes linear polarization parallel to the crystallographic

axis [1 0 0] and [0 1 0], respectively; \({X}^{{\prime} }\) and \({Y}^{{\prime} }\) denotes linear polarization parallel to [1 1 0] and [1 \(\bar{1}\) 0], respectively; _R_ = _X_ + _i__Y_

and _L_ = _X_ − _i__Y_ denote the right- and left-circular polarizations, respectively; The _Z_ direction corresponds to the _c_ axis perpendicular to the (1 0 0) plane. TRANSMISSION

ELECTRON MICROSCOPY MEASUREMENT Single crystal of Mo3Al2C were polished, followed by Ar-ion milling, and studied using a JEOL-2010F field-emission TEM equipped cryogenic sample stage.

GROUP-THEORETICAL ANALYSIS Group theoretical predictions were performed using the tool provided in the Isotropy Software Suite and the Bilbao Crystallographic Server50,51,52. The correlation

table [Table 1] lists all ten nontrivial subgroups of _O_ and provides the correspondences of irreducible representations. Each subgroup is generated by a subset of the symmetry elements of

the parent group, as indicated in the table header. Cubic point groups have a complicated product structure involving a tetragonal (or orthorhombic) and a trigonal subsymmetry. Notably,

there are two distinct _D_2 subgroups within _O_; one is associated with the tetragonal subsymmetry, while the other combines symmetry elements from both classes. Additionally, the table

includes a redundant \({D}_{4}^{*}\) group, which, although identical to the standard-oriented _D_4, is constructed from different generators; the only difference between the two entries

lies in the _B_1 and _B_2 labels. Based on Table 1, only the _C_3 and _D_3 subgroups show that _E_ irreducible representation does not split while _T_2 irreducible representation splits into

two irreducible representations. FIRST-PRINCIPLES CALCULATIONS First-principles calculations were performed using the VASP code which uses projector-augmented wave formalism53,54,55,56.

DFT+U formalism was not used due to the metallic nature of Mo3Al2C with only 4_d_ transition metal cations. Similarly, spin-orbit coupling was ignored. The PBEsol exchange correlation

functional57 was used due to the success of this generalized gradient approximation in reproducing the lattice parameters of solids, which is particularly important when studying lattice

instabilities. The direct method, which involves displacing atoms one by one and using the Hellmann-Feynman forces to obtain force constants, was employed to calculate the phonon

frequencies. A Gaussian smearing of 200 meV for the electronic occupations was employed, along with a 8 × 8 × 8 k-grid to approximate the Brillouin zone integrals. While the unstable phonon

frequencies exhibit some sensitivity to these parameters, which is often the case for CDW instabilities58, our calculations with lower values of smearing or denser k-grids did not give

qualitatively distinct results. DATA AVAILABILITY The transport and Raman data generated in this study have been deposited in the figshare database under accession code

https://doi.org/10.6084/m9.figshare.27192603. More data are available from the corresponding authors upon request. REFERENCES * Anderson, P. W. & Blount, E. I. Symmetry considerations on

martensitic transformations: “ferroelectric" metals? _Phys. Rev. Lett._ 14, 217–219 (1965). Article  ADS  CAS  Google Scholar  * Benedek, N. A. & Birol, T. ‘ferroelectric’ metals

reexamined: fundamental mechanisms and design considerations for new materials. _J. Mater. Chem. C._ 4, 4000–4015 (2016). Article  CAS  Google Scholar  * Zhou, W. X. & Ariando, A. Review

on ferroelectric/polar metals. _Jpn. J. Appl. Phys._ 59, SI0802 (2020). Article  CAS  Google Scholar  * Ghosez, P. & Junquera, J. Modeling of ferroelectric oxide perovskites: from first

to second principles. _Annu. Rev. Condens. Matter Phys._ 13, 325–364 (2022). Article  ADS  CAS  Google Scholar  * Bhowal, S. & Spaldin, N. A. Polar metals: principles and prospects.

_Annu. Rev. Mater. Res._ 53, 53–79 (2023). Article  ADS  CAS  Google Scholar  * Hickox-Young, D., Puggioni, D. & Rondinelli, J. M. Polar metals taxonomy for materials classification and

discovery. _Phys. Rev. Mater._ 7, 010301 (2023). Article  CAS  Google Scholar  * Li, S. & Birol, T. Free-carrier-induced ferroelectricity in layered perovskites. _Phys. Rev. Lett._ 127,

087601 (2021). Article  ADS  PubMed  CAS  Google Scholar  * Shi, Y. et al. A ferroelectric-like structural transition in a metal. _Nat. Mater._ 12, 1024–1027 (2013). Article  ADS  PubMed 

CAS  Google Scholar  * Puggioni, D. & Rondinelli, J. M. Designing a robustly metallic noncenstrosymmetric ruthenate oxide with large thermopower anisotropy. _Nat. Commun._ 5, 3432

(2014). Article  ADS  PubMed  Google Scholar  * Kim, T. H. et al. Polar metals by geometric design. _Nature_ 533, 68–72 (2016). Article  ADS  PubMed  CAS  Google Scholar  * Fei, Z. et al.

Ferroelectric switching of a two-dimensional metal. _Nature_ 560, 336–339 (2018). Article  ADS  PubMed  CAS  Google Scholar  * Sakai, H. et al. Critical enhancement of thermopower in a

chemically tuned polar semimetal MoTe2. _Sci. Adv._ 2, e1601378 (2016). Article  ADS  PubMed  PubMed Central  Google Scholar  * Cheong, S.-W. & Mostovoy, M. Multiferroics: a magnetic

twist for ferroelectricity. _Nat. Mater._ 6, 13–20 (2007). Article  ADS  PubMed  CAS  Google Scholar  * van den Brink, J. & Khomskii, D. I. Multiferroicity due to charge ordering. _J.

Phys. Condens. Matter_ 20, 434217 (2008). Article  Google Scholar  * Fiebig, M., Lottermoser, T., Meier, D. & Trassin, M. The evolution of multiferroics. _Nat. Rev. Mater._ 1, 16046

(2016). Article  ADS  CAS  Google Scholar  * Qi, Y. & Rabe, K. M. Electron-lattice coupling effects in nonadiabatic polarization switching of charge-order-induced ferroelectrics. _Phys.

Rev. B_ 106, 125131 (2022). Article  ADS  CAS  Google Scholar  * Liu, Q.-M. et al. Room temperature nonvolatile optical control of polar order in a charge density wave. _Nat. Commun_. 15,

8937 (2024) * Enderlein, C. et al. Superconductivity mediated by polar modes in ferroelectric metals. _Nat. Commun._ 11, 4852 (2020). Article  ADS  PubMed  PubMed Central  CAS  Google

Scholar  * Salmani-Rezaie, S., Ahadi, K. & Stemmer, S. Polar nanodomains in a ferroelectric superconductor. _Nano Lett._ 20, 6542–6547 (2020). Article  ADS  PubMed  CAS  Google Scholar 

* Hameed, S. et al. Enhanced superconductivity and ferroelectric quantum criticality in plastically deformed strontium titanate. _Nat. Mater._ 21, 54–61 (2022). Article  ADS  PubMed  CAS 

Google Scholar  * Jindal, A. et al. Coupled ferroelectricity and superconductivity in bilayer T_d_-MoTe2. _Nature_ 613, 48–52 (2023). Article  ADS  PubMed  CAS  Google Scholar  * Smidman,

M., Salamon, M. B., Yuan, H. Q. & Agterberg, D. F. Superconductivity and spin-orbit coupling in non-centrosymmetric materials: a review. _Rep. Prog. Phys._ 80, 036501 (2017). Article 

ADS  PubMed  CAS  Google Scholar  * Edelstein, V. M. The Ginzburg–Landau equation for superconductors of polar symmetry. _J. Phys. Condens. Matter_ 8, 339 (1996). Article  ADS  CAS  Google

Scholar  * Tokura, Y. & Nagaosa, N. Nonreciprocal responses from non-centrosymmetric quantum materials. _Nat. Commun._ 9, 3740 (2018). Article  ADS  PubMed  PubMed Central  Google

Scholar  * Itahashi, Y. M. et al. Nonreciprocal transport in gate-induced polar superconductor SrTiO3. _Sci. Adv._ 6, eaay9120 (2020). Article  ADS  PubMed  PubMed Central  Google Scholar  *

Nagaosa, N. & Yanase, Y. Nonreciprocal transport and optical phenomena in quantum materials. _Annu. Rev. Condens. Matter Phys._ 15, 63–83 (2024). Article  ADS  CAS  Google Scholar  *

Nadeem, M., Fuhrer, M. S. & Wang, X. The superconducting diode effect. _Nat. Rev. Phys._ 5, 558–577 (2023). Article  Google Scholar  * Yip, S. Noncentrosymmetric superconductors. _Annu.

Rev. Condens. Matter Phys._ 5, 15–33 (2014). Article  ADS  CAS  Google Scholar  * Yuan, H. Q. et al. _S_-wave spin-triplet order in superconductors without inversion symmetry: Li2Pd3B and

Li2Pt3B. _Phys. Rev. Lett._ 97, 017006 (2006). Article  ADS  PubMed  CAS  Google Scholar  * Togano, K. et al. Superconductivity in the metal rich Li-Pd-B ternary boride. _Phys. Rev. Lett._

93, 247004 (2004). Article  ADS  PubMed  CAS  Google Scholar  * Karki, A. B. et al. Structure and physical properties of the noncentrosymmetric superconductor Mo3Al2C. _Phys. Rev. B_ 82,

064512 (2010). Article  ADS  Google Scholar  * Carnicom, E. M. et al. TaRh2B2 and NbRh2B2: superconductors with a chiral noncentrosymmetric crystal structure. _Sci. Adv._ 4, eaar7969 (2018).

Article  ADS  PubMed  PubMed Central  Google Scholar  * Zhigadlo, N. D., Logvinovich, D., Stepanov, V. A., Gonnelli, R. S. & Daghero, D. Crystal growth, characterization, and

point-contact Andreev-reflection spectroscopy of the noncentrosymmetric superconductor Mo3Al2C. _Phys. Rev. B_ 97, 214518 (2018). Article  ADS  CAS  Google Scholar  * Koyama, T. et al.

Normal and superconducting properties of the noncentrosymmetric Mo3Al2C. _J. Phys. Soc. Jpn._ 82, 073709 (2013). Article  ADS  Google Scholar  * Koyama, T. et al. Partial gap opening on the

Fermi surface of the noncentrosymmetric superconductor Mo3Al2C. _Phys. Rev. B_ 84, 212501 (2011). Article  ADS  Google Scholar  * Reith, D., Blaas-Schenner, C. & Podloucky, R. Density

functional theory study of phase stability, vibrational, and electronic properties of Mo3Al2C. _Phys. Rev. B_ 86, 104105 (2012). Article  ADS  Google Scholar  * Huang, F.-T. et al. Polar and

phase domain walls with conducting interfacial states in a Weyl semimetal MoTe2. _Nat. Commun._ 10, 4211 (2019). Article  ADS  PubMed  PubMed Central  Google Scholar  * Eiter, H.-M. et al.

Alternative route to charge density wave formation in multiband systems. _Proc. Natl. Acad. Sci. USA_ 110, 64–69 (2013). Article  ADS  PubMed  CAS  Google Scholar  * Devereaux, T. P. &

Hackl, R. Inelastic light scattering from correlated electrons. _Rev. Mod. Phys._ 79, 175–233 (2007). Article  ADS  CAS  Google Scholar  * Kuo, C. N., Liu, H. F. & Lue, C. S. NMR

characteristics in noncentrosymmetric Mo3Al2C. _Phys. Rev. B_ 85, 052501 (2012). Article  ADS  Google Scholar  * Mialitsin, A. Raman scattering from layered superconductors: effects of

charge ordering, two-band superconductivity, and structural disorder (Ph.D. thesis, Rutgers University-Graduate School-New Brunswick, 2010).

https://rucore.libraries.rutgers.edu/rutgers-lib/30272/ * Snow, C. S., Karpus, J. F., Cooper, S. L., Kidd, T. E. & Chiang, T.-C. Quantum melting of the charge-density-wave state in

1_T_–TiSe2. _Phys. Rev. Lett._ 91, 136402 (2003). Article  ADS  PubMed  CAS  Google Scholar  * Wu, S. et al. Symmetry breaking and ascending in the magnetic kagome metal FeGe. _Phys. Rev. X_

14, 011043 (2024). CAS  Google Scholar  * Liu, H. M. et al. Metallic ferroelectricity induced by anisotropic unscreened coulomb interaction in LiOsO3. _Phys. Rev. B_ 91, 064104 (2015).

Article  ADS  Google Scholar  * Sim, H. & Kim, B. G. First-principles study of octahedral tilting and ferroelectric-like transition in metallic LiOsO3. _Phys. Rev. B_ 89, 201107 (2014).

Article  ADS  Google Scholar  * Bauer, E. et al. Unconventional superconducting phase in the weakly correlated noncentrosymmetric Mo3Al2C compound. _Phys. Rev. B_ 82, 064511 (2010). Article

  ADS  Google Scholar  * Bonalde, I. et al. Evidence for conventional superconducting behavior in noncentrosymmetric Mo3Al2C. _Phys. Rev. B_ 84, 134506 (2011). Article  ADS  Google Scholar 

* Gupta, R., Ying, T. P., Qi, Y. P., Hosono, H. & Khasanov, R. Gap symmetry of the noncentrosymmetric superconductor W3Al2C. _Phys. Rev. B_ 103, 174511 (2021). Article  ADS  CAS  Google

Scholar  * Kallin, C. & Berlinsky, J. Chiral superconductors. _Rep. Prog. Phys._ 79, 054502 (2016). Article  ADS  PubMed  Google Scholar  * Kroumova, E. et al. Bilbao crystallographic

server: Useful databases and tools for phase-transition studies. _Phase Transit._ 76, 155–170 (2003). Article  CAS  Google Scholar  * Aroyo, M. I. et al. Crystallography online: Bilbao

crystallographic server. _Bulg. Chem. Commun._ 43, 183–97 (2011). CAS  Google Scholar  * Hatch, D. M. & Stokes, H. T. Invariants: program for obtaining a list of invariant polynomials of

the order-parameter components associated with irreducible representations of a space group. _J. Appl. Crystallogr._ 36, 951–952 (2003). Article  ADS  CAS  Google Scholar  * Kresse, G.

& Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. _Comput. Mater. Sci._ 6, 15–50 (1996). Article  CAS 

Google Scholar  * Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. _Phys. Rev. B_ 54, 11169–11186 (1996).

Article  ADS  CAS  Google Scholar  * Blöchl, P. E. Projector augmented-wave method. _Phys. Rev. B_ 50, 17953 (1994). Article  ADS  Google Scholar  * Kresse, G. & Joubert, D. From

ultrasoft pseudopotentials to the projector augmented-wave method. _Phys. Rev. B_ 59, 1758 (1999). Article  ADS  CAS  Google Scholar  * Perdew, J. P. et al. Restoring the density-gradient

expansion for exchange in solids and surfaces. _Phys. Rev. Lett._ 100, 136406 (2008). Article  ADS  PubMed  Google Scholar  * Christensen, M. H., Birol, T., Andersen, B. M. & Fernandes,

R. M. Theory of the charge density wave in _A_V3Sb5 kagome metals. _Phys. Rev. B_ 104, 214513 (2021). Article  ADS  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS The

spectroscopic work conducted at Rutgers (S.F.W. and G.B.) was supported by the NSF Grant No. DMR-2105001. The sample growth, characterization, and TEM work (X.H.X. F.T.H and S.W.C.) were

supported by the DOE under Grant No. DOE: DE-FG02-07ER46382. The theoretical work conducted at the University of Minnesota (E.R. and T.B.) was supported by the NSF CAREER Grant No.

DMR-2046020. The work at NICPB was supported by the European Research Council (ERC) under the European Union’s Horizon 2020 Research and Innovation Programme grant agreement No. 885413.

AUTHOR INFORMATION Author notes * Shangfei Wu Present address: Beijing Academy of Quantum Information Sciences, Beijing, China * Xianghan Xu Present address: School of Physics and Astronomy,

University of Minnesota, Minneapolis, MN, USA * Ethan T. Ritz Present address: Department of Engineering, Harvey Mudd College, Claremont, CA, USA AUTHORS AND AFFILIATIONS * Department of

Physics and Astronomy, Rutgers University, Piscataway, NJ, USA Shangfei Wu, Fei-Ting Huang, Xianghan Xu, Sang-Wook Cheong & Girsh Blumberg * Keck Center for Quantum Magnetism, Rutgers

University, Piscataway, NJ, USA Fei-Ting Huang, Xianghan Xu & Sang-Wook Cheong * Department of Chemical Engineering and Materials Science, University of Minnesota, Minneapolis, MN, USA

Ethan T. Ritz & Turan Birol * National Institute of Chemical Physics and Biophysics, Tallinn, Estonia Girsh Blumberg Authors * Shangfei Wu View author publications You can also search

for this author inPubMed Google Scholar * Fei-Ting Huang View author publications You can also search for this author inPubMed Google Scholar * Xianghan Xu View author publications You can

also search for this author inPubMed Google Scholar * Ethan T. Ritz View author publications You can also search for this author inPubMed Google Scholar * Turan Birol View author

publications You can also search for this author inPubMed Google Scholar * Sang-Wook Cheong View author publications You can also search for this author inPubMed Google Scholar * Girsh

Blumberg View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS G.B. and S.W.C. designed and supervised the experiments. S.F.W. and G.B. acquired

and analyzed the Raman data. X.H.X. and S.W.C. synthesized the single crystal. F.T.H. and S.W.C. acquired and analyzed the TEM data. E.R. and T.B. did the supercell, domain, and free-energy

model analysis and first-principles phonon calculations. All authors contributed to the discussion and writing of the manuscript. CORRESPONDING AUTHORS Correspondence to Shangfei Wu, Turan

Birol, Sang-Wook Cheong or Girsh Blumberg. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. PEER REVIEW PEER REVIEW INFORMATION _Nature Communications_

thanks Shunsaku Kitagawa, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available. ADDITIONAL INFORMATION PUBLISHER’S

NOTE Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION TRANSPARENT

PEER REVIEW FILE RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any

non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the

Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of

it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material

is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission

directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wu,

S., Huang, FT., Xu, X. _et al._ Polar charge density wave in a superconductor with crystallographic chirality. _Nat Commun_ 15, 9276 (2024). https://doi.org/10.1038/s41467-024-53627-1

Download citation * Received: 08 July 2024 * Accepted: 16 October 2024 * Published: 28 October 2024 * DOI: https://doi.org/10.1038/s41467-024-53627-1 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative