Reader TTS

ABSTRACT We propose an ideal scheme for preparing vibrational SU(1, 1) ⊗ SU(1, 1) states in a two-dimensional ion trap using red and blue second sideband resolved driving of two orthogonal

vibrational modes. Symmetric and asymmetric driving provide two regimes to realize quantum state engineering of the vibrational modes. In one regime, we show that time evolution synthesizes

so-called SU(1, 1) Perelomov coherent states, that is separable squeezed states and their superposition too. The other regime allows engineering of lossless 50/50 SU(2) beam splitter states

that are entangled states. These ideal dynamics are reversible, thus, the non-classical and entangled states produced by our schemes might be used as resources for interferometry. SIMILAR

CONTENT BEING VIEWED BY OTHERS SUB-OPTICAL-CYCLE LIGHT-MATTER ENERGY TRANSFER IN MOLECULAR VIBRATIONAL SPECTROSCOPY Article Open access 06 October 2022 POPULATION DIFFERENCE GRATINGS CREATED

ON VIBRATIONAL TRANSITIONS BY NONOVERLAPPING SUBCYCLE THZ PULSES Article Open access 21 January 2021 CONTROLLING FLOQUET STATES ON ULTRASHORT TIME SCALES Article Open access 19 November

2022 INTRODUCTION Quantum state engineering studies the preparation, manipulation, and characterization of arbitrary quantum states. Technological advances allow the coherent control of

dynamics in an increasing collection of physical systems; e.g. trapped ions, superconducting circuits, quantum gases, mechanical oscillators. In particular, trapped ions show high

addressability, long coherence times and high fidelity readout necessary for quantum state preparation and manipulation within its own experimental issues1. Vibrational state

characterization is available in this platform through tomographic reconstruction, experimentally demonstrated for Wigner2 and Hussimi3 quasi-probability distributions. Trapped ions have

proved a fertile ground for fundamental research and quantum technologies development4,5. Single-mode vibrational number, coherent, and squeezed states have been engineered experimentally6

and theoretical proposals for the synthesis of arbitrary one7- and two-dimensional vibrational states8 has been produced. In particular, trapped ions might act as vibrational beam splitters9

producing states identical to the photon states on the output ports of a lossless interferometer with number-state inputs10. Vibrational interferometry can be used to either explore

fundamental quantum mechanics, e.g. quantum decoherence11,12, or produce new quantum technologies, e.g. vibrational thermometers13 or quantum gyroscopes14. Squeezing and entanglement improve

phase sensitivity in interferometry in a manner proportional to the inverse of the excitation number of quanta entering an interferometer15,16,17. Here, we are interested in the quantum

state engineering of orthogonal vibrational modes that show squeezing and entanglement with an underlying SU(1, 1) ⊗ SU(1, 1) symmetry. We will use blue and red resolved second sideband

driving18,19 to this end. In the following, we will present an effective Hamiltonian describing our proposal in the Lamb-Dicke regime. Then, we will show that the asymmetric coupling model

produces the superposition of separable squeezed vibrational mode states where the inner state is intrinsically entangled to the vibrational modes. Afterward, we will show that red driving

with symmetric coupling is able to produce lossless 50/50 SU(2) beam splitter vibrational states that are factorized from the internal state of the ion. The ideal dynamics producing these

states are reversible and seem to suggest their use as interferometers to characterize different aspects of real-world experiments. RESULTS We suggest driving two normal phonon modes of the

center of mass motion of a trapped ion20,21, such that the effective Hamiltonian, $${\hat{H}}_{ion}=\frac{{\omega }_{0}}{2}{\hat{\sigma }}_{3}+{\sum }_{j=1}^{2}{\nu

}_{j}{\hat{a}}_{j}^{\dagger }{\hat{a}}_{j}+{{\rm{\Omega }}}_{j}\,\cos \,[{\eta }_{j}({\hat{a}}_{j}^{\dagger }+{\hat{a}}_{j})-{\omega }_{j}t+{\varphi }_{j}]{\hat{\sigma }}_{j},$$ (1)

describes the interaction of the _j_-th vibrational mode, with frequency _ν__j_ and represented by the annihilation (creation) operator \({\hat{a}}_{j}\) \(({\hat{a}}_{j}^{\dagger })\), with

two internal levels of the trapped ion, with energy gap _ω_0 and represented by Pauli matrices \({\hat{\sigma }}_{j}\), through a set of external driving fields of frequency _ω__j_,

Lamb-Dicke parameter _η__j_, phase _ϕ__j_, and Rabi coupling strength Ω_j_. Moving into the reference frame defined by the uncoupled Hamiltonian, \({\hat{H}}_{0}={\omega }_{0}{\hat{\sigma

}}_{3}/2+{\nu }_{1}{\hat{a}}_{1}^{\dagger }{\hat{a}}_{1}+{\nu }_{2}{\hat{a}}_{2}^{\dagger }{\hat{a}}_{2}\), driving the _k_-th vibrational sideband, _ω__j_ = _ω_0 − _kν__j_ where _k_ > 0

and _k_ < 0 define the so-called red and blue driving, in the Lamb-Dicke regime, \({\eta }_{j}\sqrt{\langle {\hat{a}}_{j}^{\dagger }{\hat{a}}_{j}\rangle }\ll 1\), and under an optical and

mechanical rotating wave approximation, we can approximate22 for red, $${\hat{H}}_{R}\approx \sum _{j=1}^{2}\,\frac{{g}_{j,k}}{2}[{e}^{i{\varphi }_{j,k}}{\hat{a}}_{j}^{k}{\hat{\sigma

}}_{+}+{e}^{-i{\varphi }_{j,k}}{\hat{a}}_{j}^{\dagger k}{\hat{\sigma }}_{-}],$$ (2) and blue sideband driving, $${\hat{H}}_{B}\approx \sum _{j=1}^{2}\,\frac{{g}_{j,k}}{2}[{e}^{i{\varphi

}_{j,k}}{\hat{a}}_{j}^{\dagger |k|}{\hat{\sigma }}_{+}+{e}^{-i{\varphi }_{j,k}}{\hat{a}}_{j}^{|k|}{\hat{\sigma }}_{-}],$$ (3) with effective couplings and phases, \({g}_{j,k}\approx

{{\rm{\Omega }}}_{j}{\eta }_{j}^{|k|}{e}^{-|{\eta }_{j}{|}^{2}/2}/|k|!\) and \({e}^{i{\varphi }_{j,k}}={(-i)}^{j-1+|k|}{e}^{i{\varphi }_{j}}\), in that order. For reasons that will become

obvious, we choose the second sideband driving19, _k_ = ±2, and draw from the idea of simultaneous blue and red driving in the simulation of the quantum Rabi model23,24 to reach the model

Hamiltonian at the core of our proposal, $$\hat{H}=\sum _{j=1}^{2}\,\frac{{g}_{j\mathrm{,2}}}{2}[{e}^{i{\varphi }_{j\mathrm{,2}}}{\hat{a}}_{j}^{2}{\hat{\sigma }}_{+}+{e}^{-i{\varphi

}_{j\mathrm{,2}}}{\hat{a}}_{j}^{\dagger 2}{\hat{\sigma }}_{-}]+\frac{{g}_{j,-2}}{2}[{e}^{i{\varphi }_{j,-2}}{\hat{a}}_{j}^{\dagger 2}{\hat{\sigma }}_{+}+{e}^{-i{\varphi

}_{j,-2}}{\hat{a}}_{j}^{2}{\hat{\sigma }}_{-}].$$ (4) This model is the two-phonon interaction analog of the so-called cross-cavity quantum Rabi model25 that has been used to propose the

quantum simulation of para-oscillators in trapped ions26,27. Single-mode, two-phonon interactions in trapped ions have been recently proposed to simulate interaction-induced spectral

collapse28. It may be possible to explore alternative schemes in the trapped-ion platform; for example, continuous dynamical decoupling schemes that have been proposed as alternatives to

produce robust realizations of the two-phonon interaction in the ultrastrong regime29 or dynamics far away from the Lamb-Dicke regime30. It might be even possible to explore realizations

with superconducting qubits, where a two-photon quantum Rabi model has been proposed31, or single trapped cold atoms, where a proposal to realize the quantum Rabi model has arisen32.

DISCUSSION ASYMMETRIC SQUEEZING Let us simplify and find uses for our general Hamiltonian. First, we propose to work with a system where the amplitudes and relative phases for blue and red

driving in each mode are chosen to provide similar coupling parameters, _g__j_,_k_ ≡ _g__j_, and phases, _ϕ__j_,_k_ ≡ _π_/2. Under this assumption, the Hamiltonian describing the system,

$${\hat{H}}_{1}=i[\frac{{g}_{1}}{2}({\hat{a}}_{1}^{\dagger 2}-{\hat{a}}_{1}^{2})+\frac{{g}_{2}}{2}({\hat{a}}_{2}^{\dagger 2}-{\hat{a}}_{2}^{2})]{\hat{\sigma }}_{1},$$ (5) yields an evolution

operator, $${\hat{U}}_{1}(t)={\hat{S}}_{1}({g}_{1}t{\hat{\sigma }}_{1}){\hat{S}}_{2}({g}_{2}t{\hat{\sigma }}_{1}),$$ (6) that is the product of two standard SU(1, 1) squeezing operators,

\({\hat{S}}_{j}(\alpha )=\exp [\alpha ({\hat{a}}_{j}^{\dagger 2}-{\hat{a}}_{j}^{2})/2]\) controlled by the internal state of the trapped ion. For example, choosing an initial state with

arbitrary phonon fields and the internal state an eigenstate of the \({\hat{\sigma }}_{1}\) operator, |_ψ_(0)〉 = |_ξ_1, _ξ_2, _x_±〉, the ideal evolution, $$|\psi (t)\rangle

={\hat{S}}_{1}(\,\pm \,{g}_{1}t){\hat{S}}_{2}(\,\pm \,{g}_{2}t)|{\xi }_{1},{\xi }_{2},{x}_{\pm }\rangle ,$$ (7) provides a separable state with different squeezing in each mode. These are

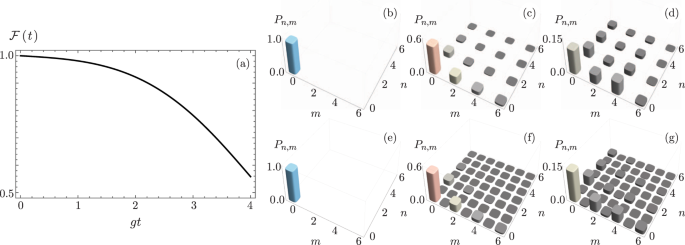
the so-called two-mode SU(1, 1) Perelomov coherent states, whose properties have been discussed in detail by Gerry and Benmoussa33. Figure 1(a) shows the fidelity defined as the trace

distance, $$ {\mathcal F} (t)={\rm{Tr}}[{\hat{\rho }}_{\psi }(t){\hat{\rho }}_{\gamma }(t)],$$ (8) between the density operator describing the ideal evolution, \({\hat{\rho }}_{\psi

}(t)=|\psi (t)\rangle \langle \psi (t)|\), and that for evolution under atomic decay, \({\hat{\rho }}_{\gamma }(t)\) such that \(\dot{\rho }=-\,i[\hat{H},\hat{\rho }]+{\gamma

}_{q}({\hat{\sigma }}_{-}\hat{\rho }{\hat{\sigma }}_{+}-\{{\hat{\sigma }}_{+}{\hat{\sigma }}_{-},\hat{\rho }\}/2)+{\sum }_{j}{\gamma }_{j}({\hat{a}}_{j}\hat{\rho }{\hat{a}}_{j}^{\dagger

}-\{{\hat{a}}_{j}^{\dagger }{\hat{a}}_{j},\hat{\rho }\}/2)\) where _γ__q_ and _γ__j_ are the effective atomic and vibrational decay rates. The parameters in the simulations are _g_2 = 0.75

_g_1 and, for the sake of the example, homogeneous decays _γ__q_ = _γ__j_ = _γ_ = 0.1 _g_1. While we select these parameter values for the sake of showing the dynamics in a lossy system,

they are not far from those of trapped Barium34 or Cadmium35 where Rabi frequencies are of the order of 15–100 kHz and the coherence time of the qubits are in the 80–120 _μ_s range. Note

that Fig. 1(b–d) show the joint phonon number probability, $${P}_{n,m}(t)={\rm{Tr}}[|m,n\rangle \langle m,n|\hat{\rho }],$$ (9) for ideal and Fig. 1(e–g) for lossy evolution at different

times. We colored the probability bars and show only a small section of the plot to make comparison simpler. Obviously, choosing an arbitrary internal initial state, |_ψ_(0)〉 = |_ξ_1,

_ξ_2〉(_α_|_x_+〉 + _β_|_x_−〉), provides a superposition of the form, $$|\psi (t)\rangle =\alpha {\hat{S}}_{1}({g}_{1}t){\hat{S}}_{2}({g}_{2}t)|{\xi }_{1},{\xi }_{2},{x}_{+}\rangle -\beta

{\hat{S}}_{1}^{\dagger }({g}_{1}t){\hat{S}}_{2}^{\dagger }({g}_{2}t)|{\xi }_{1},{\xi }_{2},{x}_{-}\rangle ,$$ (10) where the state of the whole system is entangled thanks to the internal

state of the ion. Figure 2(a) shows the fidelity between the ideal and lossy evolution. Figure 2(b–d) show the joint phonon number probability, for ideal and Fig. 2(e–g) for lossy evolution.

Parameters are identical to those in Fig. 1. The fact that a _π_-phase change in the driving laser phases ideally reverts the effective model dynamics might suggest its use as a squeezed

state interferometer. In a real-world experiment, the system will not return to the original initial state due to all the real-world experimental subtleties. For example, these states might

help in the characterization of the environment effect on the trapped center of mass motion and internal states of the ion might mention the obvious. SYMMETRIC SQUEEZING Now, let us simplify

our model one step more and assume a system where the coupling parameters, _g__j_,_k_ ≡ _g_, and the phases are chosen to be equal. The dynamics are given by a simpler Hamiltonian that

produces symmetric squeezing if we follow the procedure introduced before. We can take a second step and suppress blue sideband driving, then the dynamics are described by a Hamiltonian,

$${\hat{H}}_{2}=\frac{g}{2}[({\hat{a}}_{1}^{\dagger 2}+{\hat{a}}_{2}^{\dagger 2}){\hat{\sigma }}_{-}+({\hat{a}}_{1}^{2}+{\hat{a}}_{2}^{2}){\hat{\sigma }}_{+}].$$ (11) Again, it is

straightforward to construct an evolution operator, $${\hat{U}}_{2}(t)=(\begin{array}{cc}\cos \,gt\sqrt{{\hat{K}}_{-}{\hat{K}}_{+}} & -i\,\sin

\,gt\sqrt{{\hat{K}}_{-}{\hat{K}}_{+}}\,\frac{1}{\sqrt{{\hat{K}}_{-}{\hat{K}}_{+}}}{\hat{K}}_{-}\\ -i{\hat{K}}_{+}\frac{1}{\sqrt{{\hat{K}}_{-}{\hat{K}}_{+}}}\,\sin

\,gt\sqrt{{\hat{K}}_{-}{\hat{K}}_{+}} & \cos \,gt\sqrt{{\hat{K}}_{+}{\hat{K}}_{-}}\end{array}),$$ (12) using a representation of SU(1, 1),

$$[{\hat{K}}_{+},{\hat{K}}_{-}]=-\,2{\hat{K}}_{3},\,\,[{\hat{K}}_{3},{\hat{K}}_{\pm }]=\pm \,{\hat{K}}_{\pm },$$ (13) provided by the two-mode operators33, $${\hat{K}}_{3}=\frac{1}{2}(\sum

_{j=1}^{2}\,{\hat{a}}_{j}^{\dagger }{\hat{a}}_{j}+1),\,{\hat{K}}_{+}=\frac{1}{2}({\hat{a}}_{1}^{\dagger 2}+{\hat{a}}_{2}^{\dagger

2}),\,{\hat{K}}_{-}=\frac{1}{2}({\hat{a}}_{1}^{2}+{\hat{a}}_{2}^{2}).$$ (14) We will use a Hilbert space partition defined by the raising operator, $$|k;m\rangle

=\sqrt{\frac{\mathrm{(2}k-\mathrm{1)!}}{m\mathrm{!(2}k+m-\mathrm{1)!}}}\,{\hat{K}}_{+}^{m}|k\mathrm{;0}\rangle ,$$ (15) acting on four states that we will call vacuum states related to a

Bargmann index _k_. This produces four phonon subspaces labelled by a Bargmann index and a vacuum state: _k_ = 1/2 and |1/2; 0〉 = |0, 0〉, _k_ = 1 and |1; 0〉01 = |0, 1〉, _k_ = 1 and |1; 0〉10 

= |1, 0〉, _k_ = 3/2 and |1, 0〉 = |1, 1〉. Figure 3 shows a pictorial representation of these phonon subspaces. The whole Hilbert state for the quantized center of mass motion is covered once

with the four orthogonal subspaces defined by the bases, $$\begin{array}{rcl}\mathrm{|1}/\mathrm{2;}m\rangle & = & \frac{1}{{2}^{m}m!}\sum _{l=0}^{m}\,(\begin{array}{c}m\\

l\end{array})\sqrt{\mathrm{(2}m-2l\mathrm{)!(2}l)!}\mathrm{\ |2}m-2l\mathrm{,\ 2}l\rangle ,\\ \mathrm{|1;}m{\rangle }_{01} & = & \frac{1}{{2}^{m}}\sum

_{l\mathrm{=0}}^{m}\,(\begin{array}{c}m\\ l\end{array})\sqrt{\frac{\mathrm{(2}m-2l+\mathrm{1)!(2}l)!}{m!(m+\mathrm{1)!}}}\mathrm{\ |2}l\mathrm{,\ 2}m-2l+1\rangle ,\\ \mathrm{|1;}m{\rangle

}_{10} & = & \frac{1}{{2}^{m}}\sum _{l\mathrm{=0}}^{m}\,(\begin{array}{c}m\\ l\end{array})\sqrt{\frac{\mathrm{(2}m-2l+\mathrm{1)!(2}l)!}{m!(m+\mathrm{1)!}}}\mathrm{\

|2}m-2l+\mathrm{1,\ 2}l\rangle ,\\ \mathrm{|3/2;}m\rangle & = & \frac{1}{{2}^{m}}\sum _{l\mathrm{=0}}^{m}\,(\begin{array}{c}m\\

l\end{array})\sqrt{\frac{\mathrm{2(2}m-2l+\mathrm{1)!(2}l+\mathrm{1)!}}{m!(m+\mathrm{2)!}}}\mathrm{\ |2}m-2l+\mathrm{1,\ 2}l+1\rangle ,\end{array}$$ (16) that are eigenstates of the

\({\hat{K}}_{3}\) operator, \({\hat{K}}_{3}|k;m\rangle =(m+k)|k;m\rangle \). Here, we want to make a stop and remember the action of a lossless SU(2) beam splitter10,36, $$\hat{T}(\theta

)=\exp [i\theta ({\hat{a}}_{1}^{\dagger }{\hat{a}}_{2}+{\hat{a}}_{1}{\hat{a}}_{2}^{\dagger })/2],$$ (17) such that for a 50/50 beam splitter, _θ_ = _π_/2, we can rewrite the SU(1, 1) bases

above, $$\begin{array}{rcl}\mathrm{|1}/\mathrm{2;}m\rangle & = & \frac{{(-i)}^{m}}{m!}\hat{T}(\pi /\mathrm{2)}({\hat{a}}_{1}^{\dagger m}{\hat{a}}_{2}^{\dagger m}){\hat{T}}^{\dagger

}(\pi \mathrm{/2)\ |0,0}\rangle ,\\ \mathrm{|1;}m{\rangle }_{01} & = & \frac{{(-i)}^{m}}{\sqrt{2m!(m+\mathrm{1)!}}}\hat{T}(\pi /\mathrm{2)}({\hat{a}}_{1}^{\dagger

m+1}{\hat{a}}_{2}^{\dagger m}-i{\hat{a}}_{1}^{\dagger m}{\hat{a}}_{2}^{\dagger m+1}){\hat{T}}^{\dagger }(\pi /\mathrm{2)\ |0,0}\rangle ,\\ \mathrm{|1;}m{\rangle }_{10} & = &

\frac{{(-i)}^{m}}{\sqrt{2m!(m+\mathrm{1)!}}}\hat{T}(\pi /\mathrm{2)}({\hat{a}}_{1}^{\dagger m}{\hat{a}}_{2}^{\dagger m+1}-i{\hat{a}}_{1}^{\dagger m+1}{\hat{a}}_{2}^{\dagger

m}){\hat{T}}^{\dagger }(\pi /\mathrm{2)\ |0,0}\rangle ,\\ \mathrm{|3}/\mathrm{2;}m\rangle & = & \frac{{(-i)}^{m+1}}{\sqrt{2m!(m+\mathrm{2)!}}}\hat{T}(\pi

/\mathrm{2)}({\hat{a}}_{1}^{\dagger m+2}{\hat{a}}_{2}^{\dagger m}-i{\hat{a}}_{1}^{\dagger m}{\hat{a}}_{2}^{\dagger m+2}){\hat{T}}^{\dagger }(\pi /\mathrm{2)\ |0,0}\rangle ,\end{array}$$ (18)

in terms of ideal 50/50 beam splitter states. We have in our hands four phonon subspaces with an underlying SU(1, 1) symmetry that resolves the Hilbert spaces of a lossless 50/50 SU(2) beam

splitter. Now, lets go back to the ideal evolution of the model and consider an initial state composed by the _m_-th state in any of the SU(1, 1) subspaces and the ion in the excited state,

|_ψ_(0)〉 = |_k_, _m_〉|_e_〉. It is straightforward to see, $$\begin{array}{ccc}|\psi (t)\rangle & = & \cos \,gt\sqrt{(m+1)(m+2k)}\,|k;m\rangle |e\rangle \\ & & -i\,\sin

\,gt\sqrt{(m+1)(m+2k)}\,|k;m+1\rangle |g\rangle ,\end{array}$$ (19) that we can scale the SU(1, 1) state ladder by a sequence of red second sideband driving and _π_-pulses, _R_1(_π_) = 

exp(_iπσ_1/2), to switch the internal state of the ion, $$\begin{array}{lll}t=0 & : & |k\mathrm{;0}\rangle |e\rangle ,\\ {U}_{2}(\frac{\pi }{2g\sqrt{2k}}) & : &

|k\mathrm{;1}\rangle |g\rangle ,\\ {e}^{i\frac{\pi }{2}{\sigma }_{1}} & : & |k\mathrm{;1}\rangle |e\rangle ,\\ {U}_{2}(\frac{\pi }{2g\sqrt{\mathrm{2(2}k+\mathrm{1)}}}) & : &

|k\mathrm{;2}\rangle |g\rangle ,\\ {e}^{i\frac{\pi }{2}{\sigma }_{1}} & : & |k\mathrm{;2}\rangle |e\rangle ,\\ {U}_{2}(\frac{\pi }{2g\sqrt{\mathrm{3(2}k+\mathrm{2)}}}) & : &

|k\mathrm{;3}\rangle |g\rangle ,\end{array}$$ (20) and so on. Now, this procedure generates entangled orthogonal vibrational states that are factorized from the internal structure of the

ion. Again, this result suggests the use of this system as an interferometer that might provide information about the characteristics of an experiment that might be, in principle, different

from those available through the superposition of squeezed states proposed before. Figure 4(a) shows the fidelity, \( {\mathcal F} (t)\), between the ideal evolution of the driving algorithm

in Eq. (20) and lossy evolution under homogeneous decay for all components. The initial state of the algorithm is the vacuum state for the subspace defined by the Bargmann parameter _k_ = 

1/2. That is, the initial state is the ion in the excited state and both vibrational modes cooled down to the vacuum state. Figure 4(b–d) show the joint phonon number probability,

_P__n_,_m_, at times where the 50/50 SU(2) beam splitter states are expected under ideal time evolution. Figure 4(e–g) show the same probabilities for lossy evolution. CONCLUSION We proposed

a trapped ion model under second sideband resolved blue and red driving of two orthogonal modes of the center mass motion in the Lamb-Dicke regime. For parameter regimes providing an

effective model with asymmetric coupling of the vibration modes with the internal state of the ion, we showed that time evolution of arbitrary vibrational states with balanced superposition

of the internal states of the ion generates a so-called two-mode SU(1, 1) Perelomov coherent state where the vibrational modes are separable. Uneven superposition of the internal states of

the ion produces a superposition where entanglement of the whole state of the ion arises. We also showed that under red driving only, the effective model is able to generate 50/50 SU(2) beam

splitter vibrational states factorized from the internal state of the ion. The fact that it is ideally possible to engineer these states with reversible dynamics suggests the use of these

models as interferometers to characterize real-world experiments. REFERENCES * Wineland, D. J. _et al_. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. _J.

Res. Natl. Inst. Stand. Tech._ 103, 259–328 (1998). Article  CAS  Google Scholar  * Leibfried, D. _et al_. Experimental determination of the motional Quantum state of a trapped atom. _Phys.

Rev. Lett._ 77, 4281–4285 (1996). Article  ADS  CAS  Google Scholar  * Lv, D. _et al_. Reconstruction of the Jaynes-Cummings field state of ionic motion in a harmonic trap. _Phys. Rev. A_

95, 043813 (2017). Article  ADS  Google Scholar  * Kielpinski, D., Monroe, C. & Wineland, D. J. Architecture for a large-scale ion-trap quantum computer. _Nature_ 417, 709–711 (2002).

Article  ADS  CAS  Google Scholar  * Blatt, R. & Roos, C. F. Quantum simulations with trapped ions. _Nature Physics_ 8, 277–284 (2012). Article  ADS  CAS  Google Scholar  * Meekhof, D.

M., Monroe, C., King, B. E., Itano, W. M. & Wineland, D. J. Generation of Nonclassical Motional States of a Trapped Atom. _Phys. Rev. Lett._ 76, 1796–1799 (1996). Article  ADS  CAS 

Google Scholar  * Law, C. K. & Eberly, J. H. Arbitrary Control of a Quantum Electromagnetic Field. _Phys. Rev. Lett._ 76, 1055–1058 (1996). Article  ADS  CAS  Google Scholar  * Drobný,

G., Hladký, B. & Bužek, V. Quantum-state synthesis of multimode bosonic fields: Preparation of arbitrary states of two-dimensional vibrational motion of trapped ions. _Phys. Rev. A_ 58,

2481–2487 (1998). Article  ADS  Google Scholar  * Gou, S.-C. & Knight, P. L. Trapped ions as vibrational beam splitters: SU(2) states in a two-dimensional ion trap. _Phys. Rev. A_ 54,

1682–1690 (1996). Article  ADS  CAS  Google Scholar  * Campos, R. A., Saleh, B. E. A. & Teich, M. C. Quantum-mechanical lossless beam splitter: SU(2) symmetry and photon statistics.

_Phys. Rev. A_ 40, 1371–1384 (1989). Article  ADS  CAS  Google Scholar  * Poyatos, J. F., Cirac, J. I., Blatt, R. & Zoller, P. Trapped ions in the strong-excitation regime: Ion

interferometry and nonclassical states. _Phys. Rev. A_ 54, 1532–1540 (1996). Article  ADS  CAS  Google Scholar  * Zeng, H. Motional wave-packet splitting and ion-trap interferometry. _Phys.

Rev. A_ 57, 388–391 (1998). Article  ADS  CAS  Google Scholar  * Johnson, K. G., Neyenhuis, B., Mizrahi, J., Wong-Campos, J. D. & Monroe, C. Sensing Atomic Motion from the Zero Point to

Room Temperature with Ultrafast Atom Interferometry. _Phys. Rev. Lett._ 115, 213001 (2015). Article  ADS  CAS  Google Scholar  * Campbell, W. C. & Hamilton, P. Rotation sensing with

traped ions. _J. Phys. B: At. Mol. and Opt. Phy._ 50, 064002 (2017). Article  ADS  Google Scholar  * Yurke, B., McCall, S. L. & Klauder, J. R. SU(2) and SU(1, 1) interferometers. _Phys.

Rev. A_ 33, 4033–4054 (1986). Article  ADS  CAS  Google Scholar  * Böhmer, B. & Leonhardt, U. Correlation interferometer for squeezed light. _Opt. Commun._ 118, 181–185 (1995). Article 

ADS  Google Scholar  * Carranza, R. & Gerry, C. C. Photon-subtracted two-mode squeezed vacuum states and applications to quantum optical interferometry. _J. Opt. Soc. Am. B_ 29,

2581–2587 (2012). Article  ADS  CAS  Google Scholar  * de Matos Filho, R. L. & Vogel, W. Second-sideband laser cooling and nonclassical motion of trapped ions. _Phys. Rev. A_ 50,

R1988–R1991 (1994). Article  ADS  Google Scholar  * de Matos Filho, R. L. & Vogel, W. Even and Odd Coherent States of the Motion of a Trapped Ion. _Phys. Rev. Lett._ 76, 608–611 (1996).

Article  ADS  Google Scholar  * Messina, A., Maniscalco, S. & Napoli, A. Interaction of bimodal fields with few-level atoms in cavities and traps. _J. Mod. Opt._ 50, 1–49 (2003). ADS 

CAS  Google Scholar  * Zhu, S.-L., Monroe, C. & Duan, L.-M. Trapped Ion Quantum Computation with Transverse Phonon Modes. _Phys. Rev. Lett._ 97, 050505 (2006). Article  ADS  Google

Scholar  * Vogel, W. & de Matos Filho, R. L. Nonlinear Jaynes-Cummings dynamics of a trapped ion. _Phys. Rev. A_ 52, 4214–4217 (1995). Article  ADS  CAS  Google Scholar  * Pedernales, J.

S. _et al_. Quantum Rabi Model with Trapped Ions. _Sci. Rep._ 5, 15472 (2015). Article  ADS  CAS  Google Scholar  * Lv, D. _et al_. Quantum Simulation of the Quantum Rabi Model in a Trapped

Ion. _Phys. Rev. X_ 8, 021027 (2018). Google Scholar  * Huerta Alderete, C. & Rodríguez-Lara, B. M. Cross-cavity quantum Rabi model. _J. Phys. A: Math. Theor._ 49, 414001 (2016).

Article  MathSciNet  Google Scholar  * Huerta Alderete, C. & Rodríguez-Lara, B. M. Quantum simulation of driven para-Bose oscillators. _Phys. Rev. A_ 95, 013820 (2017). Article  ADS 

Google Scholar  * Huerta Alderete, C. & Rodríguez-Lara, B. M. Simulating para-Fermi oscillators. _Sci. Rep._ 8, 11572 (2018). Article  ADS  CAS  Google Scholar  * Felicetti, S. _et al_.

Spectral collapse via two-phonon interactions in trapped ions. _Phys. Rev. A_ 92, 033817 (2015). Article  ADS  Google Scholar  * Puebla, R., Hwang, M.-J., Casanova, J. & Plenio, M. B.

Protected ultrastrong coupling regime of the two-photon quantum Rabi model with trapped ions. _Phys. Rev. A_ 95, 063844 (2017). Article  ADS  Google Scholar  * Cheng, X.-H. _et al_.

Nonlinear quantum Rabi model in trapped ions. _Phys. Rev. A_ 97, 023624 (2018). Article  ADS  Google Scholar  * Felicetti, S., Rossatto, D. Z., Rico, E., Solano, E. & Forn-Díaz, P.

Two-photon quantum Rabi model in trapped ions. _Phys. Rev. A_ 97, 013851 (2018). Article  ADS  Google Scholar  * Schneeweiss, P., Dareau, A. & Sayrin, C. Cold-atom based implementation

of the quantum Rabi model. _Phys. Rev. A_ 98, 021801 (2018). Article  ADS  Google Scholar  * Gerry, C. C. & Benmoussa, A. Two-mode coherent states for SU(1; 1) ⊗ SU(1; 1). _Phys. Rev. A_

62, 033812 (2000). Article  ADS  Google Scholar  * Dietrich, M. R., Kurz, N., Noel, T., Shu, G. & Blinov, B. B. Hyperfine and optical barium ion qubits. _Phys. Rev. A_ 81, 052328

(2010). Article  ADS  Google Scholar  * Deslauriers, L. _et al_. Zero-point cooling and low heating of trapped 111Cd+ ions. _Phys. Rev. A_ 70, 043408 (2004). Article  ADS  Google Scholar  *

Luis, A. & Sanchez-Soto, L. L. A quantum description of the beam splitter. _Quantum and Semiclass. Opt.: Journal of the European Optical Society Part B_ 7, 153 (1995). Article  ADS 

Google Scholar  Download references ACKNOWLEDGEMENTS C.H.A. acknowledges financial support from CONACYT doctoral grant No. 455378 and B.M.R.-L. from CONACYT CB-2015-01/255230 and CONACYT

FORDECYT-296355. AUTHOR INFORMATION Author notes * C. Huerta Alderete and B. M. Rodríguez-Lara contributed equally. AUTHORS AND AFFILIATIONS * Instituto Nacional de Astrofísica, Óptica y

Electrónica, Calle Luis Enrique Erro No. 1, Sta. Ma. Tonantzintla, Pue. CP 72840, Mexico C. Huerta Alderete & B. M. Rodríguez-Lara * Programa Delfín, Verano de la Investigación

Científica – Instituto Nacional de Astrofísica, Óptica y Electrónica, Calle Luis Enrique Erro No. 1, Sta. Ma. Tonantzintla, Pue. CP 72840, Mexico M. P. Morales Rodríguez * Tecnologico de

Monterrey, Escuela de Ingeniería y Ciencias, Ave. Eugenio Garza Sada 2501, Monterrey, N.L., 64849, Mexico B. M. Rodríguez-Lara Authors * C. Huerta Alderete View author publications You can

also search for this author inPubMed Google Scholar * M. P. Morales Rodríguez View author publications You can also search for this author inPubMed Google Scholar * B. M. Rodríguez-Lara View

author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS C.H.A. and B.M.R.-L. proposed the original idea, performed the initial calculations, and wrote

the manuscript. M.P.M.R. performed the main calculations under C.H.A. supervision. CORRESPONDING AUTHOR Correspondence to B. M. Rodríguez-Lara. ETHICS DECLARATIONS COMPETING INTERESTS The

authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional

affiliations. RIGHTS AND PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution

and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if

changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the

material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to

obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS

ARTICLE Huerta Alderete, C., Morales Rodríguez, M.P. & Rodríguez-Lara, B.M. Engineering SU(1, 1) ⊗ SU(1, 1) vibrational states. _Sci Rep_ 9, 2734 (2019).

https://doi.org/10.1038/s41598-019-39481-y Download citation * Received: 25 October 2018 * Accepted: 22 January 2019 * Published: 25 February 2019 * DOI:

https://doi.org/10.1038/s41598-019-39481-y SHARE THIS ARTICLE Anyone you share the following link with will be able to read this content: Get shareable link Sorry, a shareable link is not

currently available for this article. Copy to clipboard Provided by the Springer Nature SharedIt content-sharing initiative