Reader TTS

ABSTRACT A theoretical variation between the two distinct light–matter coupling regimes, namely weak and strong coupling, becomes uniquely feasible in open optical Fabry—Pérot microcavities

with low mode volume, as discussed here. In combination with monolayers of transition-metal dichalcogenides (TMDCs) such as WS2, which exhibits a large exciton oscillator strength and

binding energy, the room-temperature observation of hybrid bosonic quasiparticles, referred to as exciton–polaritons and characterized by a Rabi splitting, comes into reach. In this context,

our simulations using the transfer-matrix method show how to tailor and alter the coupling strength actively by varying the relative field strength at the excitons’ position – exploiting a

tunable cavity length, a transparent PMMA spacer layer and angle-dependencies of optical resonances. Continuously tunable coupling for future experiments is hereby proposed, capable of

real-time adjustable Rabi splitting as well as switching between the two coupling regimes. Being nearly independent of the chosen material, the suggested structure could also be used in the

context of light–matter-coupling experiments with quantum dots, molecules or quantum wells. While the adjustable polariton energy levels could be utilized for polariton-chemistry or optical

sensing, cavities that allow working at the exceptional point promise the exploration of topological properties of that point. SIMILAR CONTENT BEING VIEWED BY OTHERS STRONG LIGHT-MATTER

COUPLING IN VAN DER WAALS MATERIALS Article Open access 21 August 2024 MICROCAVITY-LIKE EXCITON-POLARITONS CAN BE THE PRIMARY PHOTOEXCITATION IN BARE ORGANIC SEMICONDUCTORS Article Open

access 11 November 2021 RADIATIVE SUPPRESSION OF EXCITON–EXCITON ANNIHILATION IN A TWO-DIMENSIONAL SEMICONDUCTOR Article Open access 24 August 2023 INTRODUCTION TUNABLE LIGHT–MATTER

INTERACTION Light–matter-interaction in optical microcavities has been the subject of nearly three decades of research, involving all kinds of quantum emitters and cavity types1,2,3. The

coupling of excited matter states and photon modes can be characterized by two regimes. The weak-coupling regime, leading to altered radiative excitation lifetimes and enhanced or suppressed

spontaneous emission due to the Purcell effect4, and the strong-coupling regime. This regime is manifested by a normal mode splitting — known as (vacuum) Rabi splitting — and coherent

reversible energy exchange between light and matter states, ultimately leading to the formation of hybrid bosonic quasiparticles5,6. A requirement is that the coupling strength is high

enough and decay rates sufficiently low. Besides quantum information and light-source developments on the application side3 it is the field of fundamental cavity quantum electrodynamics

studies7 which demands optical high-quality microcavities. The topic highly benefits from research on various confinement concepts and has strongly driven the overall developments8,9,10.

Since their discovery by Weisbuch _et al_. in 1992, exciton–polaritons in optical microcavities, also known as cavity–polaritons, have attracted considerable attention by the research

community, particularly for the first experimental realization of a Bose–Einstein condensate (BEC)11,12 and later for the first achievement of novel practical devices13,14, for room

temperature condensate15,16 as well as polariton-lasing17,18 demonstrations, owing to the light effective mass of the hybrid bosonic quasiparticles. In this context, two-dimensional

semiconductors such as WS2 and WSe2 from the family of transition-metal dichalcogenides are currently strongly under consideration for the next material system in optical

cavities19,20,21,22,23,24 with which practical room-temperature BEC experiments could be carried out. For Fabry–Pérot microcavities, several parameters such as the mirror distance in

combination with the angle of incidence for the incoming light or the emitter position inside of the cavity provide the possibility of continuous tuning of the coupling situation in

light–matter interactions. In this work, we propose two ideas how to tailor the coupling strength by the relative field strength at the exciton position. Firstly, a more intuitive approach

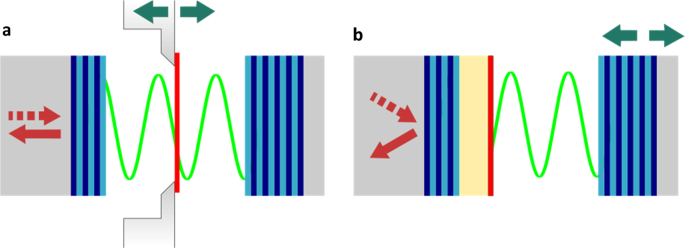
is considered, i.e. displacing a 2D material with respect to the resonator field inside an open planar microcavity with fixed mirror separation. Secondly, based on this, an open cavity with

extra spacing layer between 2D material and one mirror is introduced. This alternative setup provides the advantage that it consists only of two independent movable parts and is therefore

presumably easier to realize in an experimental setup. Furthermore it is independent from the choice of the active material. The cavity length is changed to set the excitons’ position within

the standing-wave field pattern. At the same time, spectral overlap between cavity and exciton modes occurs at different angles of incidence for the incoming cavity light. We have analyzed

this structure configuration by calculating the angle-resolved reflectivity spectra as well as the field distribution for a monolayer WS2 using the transfer-matrix method. Thereby, we show

that a transition between the weak and strong coupling regime can be observed. The coupling strength is completely tunable in our proposed setup by the choice of the spacer layer’s

thickness. These findings could enable the exploration of the transition between weak and strong coupling — especially the exceptional point — by prospective actively tunable experiments.

Furthermore, the material independent continuous adjustability could be utilized for polariton-based chemistry allowing a precise adjustment of the polariton energy levels25. This could

provide an experimental stage for an efficient study of chemical reactions influenced by different light–matter coupling situations. THEORETICAL BACKGROUND The Rabi splitting is the figure

of merit in strong-coupling experiments and is written for energetic resonance between cavity and exciton as _ħΩ__Rabi_ = _E__UP_ − _E__LP_ = 2_g__0_, whereas _E_UP and _E_LP are the

resulting energy levels of the upper and lower exciton–polariton modes, respectively. For clarity, the momentum-space dependencies of the modes, which lead to angle-dependent emission

properties, are blanked out for a moment in our discussion, while coupling does not violate energy and momentum conservation. The maximal coupling strength _g__0_ is determined, besides the

physical constants for the elementary charge _e_, the vacuum permittivity _ϵ__0_ and the electron mass _m_e, by the cavity’s permittivity _ϵ_, the exciton’s oscillator strength _f_ as well

as the cavity’s mode volume _V__eff_, $${g}_{0}=\sqrt{\frac{1}{4\pi {\epsilon }{{\epsilon }}_{0}}\frac{\pi {e}^{2}f}{{m}_{e}{V}_{eff}}}\,$$ (1) In general, the physical coupling strength _g_

is described by the maximal possible coupling strength _g__0_, the relative field strength reflecting the position inside the field pattern _ψ_(z) and the angle between the electric field

and the exciton’s dipole moment ξ2. This accounts for the anisotropy of WS2. An explicit consideration of the out-of-plane dark exciton is not necessary, because of its weak oscillator

strength26,27 as discussed in the supplement. $$g={g}_{0}\psi \,(z)cos(\xi )$$ (2) $$\psi (z)=\frac{E(z)}{|{E}_{max}|}$$ (3) The light–matter coupling is modelled by the following

Hamiltonian. $$\hat{H}=\hslash \left({\omega }_{cav}-\frac{i{\gamma }_{cav}}{2}\right){a}^{\dagger }a+\hslash \left({\omega }_{ex}-\frac{i{\gamma }_{ex}}{2}\right){\sigma }^{\dagger }\sigma

+\hslash g({\sigma }^{\dagger }a+{a}^{\dagger }\sigma )$$ (4) with the creation and annihilation operators of both species a†/σ† and a/σ, respectively. The first term describes the cavity

field with its resonance frequency _ω__cav_, the second one the exciton with its resonance frequency _ω__ex_ and the last one the coupling between both. Based on this, the eigenvalues

represent the resonance frequencies of the coupled system, $${\omega }_{\pm }=\frac{1}{2}\left({{\rm{\omega }}}_{{\rm{ex}}}+{\omega }_{cav}+\frac{i({\gamma }_{ex}+{\gamma

}_{cav})}{2}\right)\pm \frac{1}{2}\sqrt{{(2{\rm{g}})}^{2}+{\left({\omega }_{cav}-{\omega }_{ex}+i\frac{({\gamma }_{cav}-{\gamma }_{ex})}{2}\right)}^{2}}$$ (5) The coupling regime is mainly

given by the coupling strength as well as the cavity’s linewidth γ_cav_ and the exciton’s linewidth γ_ex_. In the literature, often two criteria appear: 4 g²>|γ_cav_ - γ_ex_ |2 as

condition for a splitting of the eigenvalues in Eq. (1) (e.g. in28) and 2 g²>|γ2_cav_ + γ2_ex_ | as requirement for a resolvable splitting, for which the frequency splitting is larger

than the polariton linewidth (cf.24,29). By tuning the coupling, it becomes possible to especially investigate the transition between weak and strong coupling. Between the two regimes lies

an exceptional point (EP). At this position, the coupled system only features one complex solution28,30,31. This gives rise to a variety of physical phenomena like chiral behaviour32 as well

as an energy transfer between the two modes of the strongly coupled system33 under encirclement of the EP. Due to the sharp transition between the coupling regimes, an EP is also suitable

for the design of sensors34. In order to tune from one to another coupling regime, either the excitons’ or the cavity’s properties can be altered. Tunable coupling has been demonstrated with

WS2 by applying a current35 or varying the temperature36, causing a change of the exciton oscillator strength. Furthermore, chemical reactions of molecules can be used to switch between the

coupling regimes37. Moreover, in monolithic cavities, the dependency of the coupling situation on the relative field strength has been demonstrated for molecules38. Recently, continuously

tunable coupling was shown for carbon nanotubes by utilizing the polarization of the light39. All mentioned methods above either depend on the choice of the material, need multiple growth

processes or are not actively tunable over a wide range. Here, we use properties of an open cavity to continuously tune the coupling strength and thereby are giving the perspective of

real-time switching between the strong and weak coupling regime without influencing the active region. Besides this, the presented method keeps the spectral position of the cavity mode

resonant to the exciton. Our suggested structure is _a_ _priori_ not limited to a special material. For the active medium providing the excitons only a high enough oscillator strength to

reach strong coupling as well as a sub-wavelength thickness compared to the emission wavelength is required. With the aim in mind to control the coupling situation without changing the setup

in between experiments, we chose a planar open microcavity. In combination with monolayers of transition-metal dichalcogenides such as WS2, the excitons of which exhibit a large oscillator

strength, the strong coupling regime can be reached with an open cavity already at room temperature20. 2D–MICROCAVITY STRUCTURE All simulations are done for s-polarized light in order to

exclude the influence of a misalignment between the dipole moment of excitons and the cavity mode’s electric field and thereby to ensure that they are perpendicular to each other for every

angle of incidence. The simulated Fabry–Pérot (FP) cavity consists of two dielectric mirrors (distributed Bragg reflector, short DBR), which comprise alternating layers of SiO2 and Si3N4,

with their wavelength dependent refractive indices extracted from40 and41, respectively. A similar configuration was already presented in the literature to show room-temperature polaritons

for WS220. The high-reflectivity mirrors end with the low refractive index material, namely SiO2, to ensure the field maximum at the DBRs’ surface for normal incidence. Moreover, directional

leakage of cavity photons is enabled by one side featuring less mirror pairs, resulting in a lower reflectivity for the corresponding mirror. The two mirrors therefore consist of 11.5 and

12.5 SiO2/Si3N4 layer pairs. Acting as an active medium, a monolayer of the transition-metal dichalcogenide WS2 is – in the simulations – brought into coupling with the cavity mode of the

open microresonator. Its optical behavior is modeled by an effective optical thickness of 6.18 Å42. The wavelength-dependent complex refractive index is derived from experimental data (from

ref. 42) together with an approximation of that data which consists of a summation over Lorentzian peaks according to ref. 43 (see Supporting Information Fig. SI.1). A scheme of the

simulated structure is shown in Fig. 1a. For the spacer layer in our second tunable-coupling approach, we simulated PMMA on top of one mirror (Fig. 1b). This material is already used in

waveguide applications44 or as spacer layer in monolithic cavities38 due to its transparency for visible light45. Further, it enables a wide range of possible thicknesses, from the nm-range

up to several 100 nm. The tunable coupling is achieved by variation of the angle of incidence for the incoming light combined with an adjustable cavity length. Thus, we simulated

angle-resolved reflectivity spectra to identify the coupling situation. SIMULATIONS AND DISCUSSION VARIATION OF THE 2D-MATERIAL’S POSITION As an intuitive approach, the excitons’ position

with respect to the field pattern _z_ can be varied by shifting the material inside of an open microcavity with fixed cavity length. As a result of the adjusted position, the Rabi splitting

_ħΩ__Rabi_ can be varied, which can lead to a change in the coupling regime. Figure 2a displays a plot of the system’s resonance frequencies based on the calculated reflectivity spectra of

the complete microresonator structure. At positions in the cavity corresponding to a strong coupling regime, characterized by a mode splitting, an asymmetric energy splitting into a photonic

lower polariton branch (red triangles) and an excitonic upper polariton branch (blue squares) around the exciton’s energy (dashed horizontal line) is noticeable. This is a hint, that the

system is not yet completely resonant. Here, the cavity length is determined in a way, that the resonance energy of the empty cavity without 2D material overlaps with the bare exciton mode

(dashed horizontal line), which is estimated at a wavelength of 617.2 nm (rounded) by the imaginary part of the refractive index representing the absorption. In Fig. 2a the solid black curve

represents a cavity mode with WS2 at different spatial positions for which the imaginary part of the 2D material’s refractive index is neglected. Consequently, only the reflectivity of WS2

is included for the solid black line but not its absorption. The simulated curve indicates that the 2D material’s reflectivity already detunes the spectral position of the cavity mode

without coupling considerations. This can result in a position dependent energetic offset between photon and exciton mode within the final setup. The cavity’s resonance has no offset with

respect to the exciton mode at the minima of the relative field strength (\(z\approx 0.15\,\mu m)\). At this position, the cavity is not coupled to the excitonic mode. It is worth keeping in

mind that the empty uncoupled-cavity mode has not the same spectral position as the calculated cavity for a system with active region. Beside this unreachable zero-detuning configuration

for each monolayer position (at fixed cavity length and fixed incidence angle), this approach has from the experimental point of view also the drawback of requiring a complex, rigid and

perforated holder to incorporate the free-standing material into the resonator. The calculated energy splitting normalized to the maximum (shown as dots in Fig. 2b) is nearly proportional to

the theoretical curve representing the absolute electric field strength of this cavity configuration (black line). For clarity, also here the refractive index modulation of the structure is

displayed in the background. CONCEPT MAKING USE OF AN ADDITIONAL SPACING-LAYER The optical phase shift \({\varphi }_{cav}\) between two plane parallel mirrors depends on the geometric path

difference \(\Delta {s}_{cav}\), given by the angle of incidence _ϑ_ for the incoming light, the refractive index _n_ and the cavity length _L__cav_, as well as the wavelength \(\lambda \).

$${\varphi }_{cav}=\frac{2\pi \Delta {s}_{cav}}{\lambda }=2\pi \frac{(n\cos (\vartheta )2{L}_{cav})}{\lambda }=\,2\pi \frac{(n\cos (\vartheta )2{L}_{cav})\,{E}_{cav}}{h\,c}.$$ (6) For the

resonant FP cavity mode, \({\varphi }_{cav}\) is a multiple of 2π. Waves with another wavelength _λ_ for which \({\varphi }_{cav}\) is not a multiple of 2π interfere completely or partly

destructively. If the angle of incidence \(\vartheta \) is increased, the path difference and thereby the phase shift decrease. Consequently, the wavelength of the cavity mode is reduced and

the energy of the (uncoupled) cavity mode _E__cav_ is increased (see Eq. (6)). For a longer cavity the path difference is increased leading to a reduction of the cavity mode’s energy.

Hence, the influence of _ϑ_ on _E__cav_ could be compensated by changing _L_cav (see Fig. 3). By adding an additional spacer layer, the optical path difference between the two mirror

surfaces gets the sum of the path difference inside of the PMMA-layer \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) and inside of the air gap \({\varphi }_{{\rm{A}}{\rm{i}}{\rm{r}}}\),

$${\varphi }_{cav}={\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}+{\varphi }_{{\rm{A}}{\rm{i}}{\rm{r}}}=\frac{2\pi }{\lambda }2({n}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\,\cos \,(\vartheta

){d}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}+{n}_{{\rm{A}}{\rm{i}}{\rm{r}}}\,\cos \,(\vartheta ){d}_{{\rm{A}}{\rm{i}}{\rm{r}}})$$ (7) For simplicity, the influence of the mirrors’ reflectivity on

the path difference is neglected here. Increasing _ϑ_ shortens the geometric path within the air gap \(\Delta {s}_{{\rm{A}}{\rm{i}}{\rm{r}}}\) as well as the PMMA layer \(\Delta

{s}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\). Thus, the corresponding phase shifts and thereby \({\varphi }_{cav}\) are decreased. Consequently, _E_cav is increased. Again, this could be in

principle compensated by changing _L_cav. The cavity length is given by the layer thicknesses, \({L}_{cav}={d}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}+{d}_{{\rm{A}}{\rm{i}}{\rm{r}}}\). Here, only

the gap size \({d}_{{\rm{A}}{\rm{i}}{\rm{r}}}\) is adjustable, while \({d}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) stays constant. Increasing the mirror separation leads to an increased gap

size \({d}_{{\rm{A}}{\rm{i}}{\rm{r}}}\). Accordingly, \({\varphi }_{cav}\) is increased and _E_cav is decreased. Hence, also an increased gap size could be used to compensate the phase shift

induced by an increased _ϑ_. In summary, increasing the cavity length leads to a spectral overlap between exciton resonance and cavity mode at higher angles of incidence. Here, this angle

is denoted as resonant angle _ϑ__res_. In the following, we consider only the case of spectral resonance (i.e. zero-detuning: _E__cav_ (_ϑ__res_) − _E__ex_ = 0) and thereby each change in

the cavity length corresponds to a change in _ϑ__res_. The cavity mode’s spectral position is determined by including the monolayer’s reflectivity while neglecting its absorption to exclude

the detuning observed for the structure in Fig. 1a (see Supplement Fig. SI. 6). Again, the exciton wavelength in our simulation is estimated as rounded to 617.2 nm by the peak position

within the imaginary part of the dielectric function. However, \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) and \({\varphi }_{{\rm{A}}{\rm{i}}{\rm{r}}}\) are now changed in a different

manner, although the overall phase shift \({\varphi }_{cav}\) stays the same. Increasing _ϑ_ causes a decreased \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) as well as \({\varphi

}_{{\rm{A}}{\rm{i}}{\rm{r}}}\). At the same time, the additionally increased \({L}_{cav}\) leads to an increased phase shift only within the air layer. Due to the required spectral resonance

between exciton and cavity, the total phase shift \({\varphi }_{cav}\) of the structure is kept constant. In sum, \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) is reduced whereas

\({\varphi }_{{\rm{A}}{\rm{i}}{\rm{r}}}\) is increased. Together with this mismatch between the change of phase shift inside PMMA and air, it gives rise to a shift of the field pattern

relative to the PMMA–air interface. The phase shift \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) determines the interface’s position inside of the standing wave pattern and thereby the

corresponding field amplitude. By placing the 2D material at this interface, these conditions can be utilized to adjust the coupling strength by tuning the relative field strength. This

effect is illustrated within an additional video (see Supplementary Information), showing the field pattern as well as the angle-resolved reflectivity spectra for the suggested structure.

For the field calculation the reflectivity of WS2 is again considered while its absorption is neglected. Figure 4 shows three representative settings for such a structure (see Fig. 1b). The

field pattern is moreover simulated for _ϑ__res_. Different energy splittings can be obtained in the angle-resolved reflectivity spectra. Furthermore, the angle of incidence _ϑ_ thereby not

only alters the cavity mode’s spectral position as well as the relative field strength but in general also the cavity’s linewidth _γ__cav_, because modifying _ϑ_ influences the reflectivity

of the DBR mirrors. For this setup the change is less than 0.1% within the region of experimentally interesting angles (<40°) and is thus not further discussed as impact on the coupling

regime. Nevertheless, the mirror contributes an additional phase shift for higher angle of incidences (see Supplement Fig. SI 7). Thus, spectral resonance is determined by iteratively

simulating the reflectivity spectra for varied mirror separations. However, the reflection dip in the lower row within the last image is slightly shifted with respect to the exciton energy

indicating an influence of the monolayer’s absorption on the cavity’s spectral position. ADDITIONALLY TAILORING THE COUPLING SITUATION The spacer layer’s thickness

\({d}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\) defines the starting position in the standing wave pattern at normal incidence by the corresponding phase shift \({\varphi

}_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\). At normal incidence, different air gaps are necessary for different PMMA thicknesses to reach spectral resonance. Therefore, the change in cavity

length \(\Delta z\) with respect to the length (for which resonance occurs at zero angle) \({L}_{cav}({\vartheta }_{res}=0)\) is used in Fig. 5 as a common axis (\(\Delta

z={L}_{cav}({\vartheta }_{res})-{L}_{cav}({\vartheta }_{res}=0)\)). For decreasing cavity length compared to \({L}_{cav}({\vartheta }_{res}=0)\), the energetic resonance condition can no

longer be reached, because a further increase of \(\cos (\vartheta )\) in Eq. (7) in order to compensate the phase shift compared to \(\vartheta =0\) is not possible. The simulated

relationship between \(\Delta z\) and \({\vartheta }_{res}\) is displayed within Fig. 5a. On the other hand, increasing the cavity length shifts the exciton’s location relative to the field

pattern towards the left side of the field maximum (left direction in Fig. 4a–c) due to the decreased \({\varphi }_{{\rm{P}}{\rm{M}}{\rm{M}}{\rm{A}}}\). By the choice of

\({d}_{{\rm{PMMA}}}\), it is possible to either reduce or increase the absolute field strength at the monolayer position for increasing \(\vartheta \) as well as \(\Delta z\) (see Fig. 5b).

Thus, depending on the layer’s thickness, different coupling scenarios can be reached. In Fig. 5c, the Rabi splitting for different coupling situations based on various thicknesses of the

spacer layer is shown. For example, if the PMMA–air interface lies near the field maximum at normal incidence, a length tuning leads to a decreasing relative field strength and thereby

coupling strength (e.g. blue and green curve in Fig. 5b for a 178.2 and 190.6 nm PMMA layer). Similarly, increasing coupling under cavity length tuning can be reached, for instance, by a

thickness _d_PMMA larger than one half of the wavelength in PMMA (e.g. 227.9 nm or 248.6 nm). A careful choice also enables the transition between the coupling regimes. Here, the exact

position of the transition between the coupling regimes is spectrally not directly detectable. No splitting in this context means, that it is either not resolvable or the system is weakly

coupled and thus indeed does not feature any resonance splitting. However, a systematic analysis of the lifetime in terms of Purcell effect and Hopfield coefficients should allow locating

the exceptional point. Nevertheless, the presented spacer-layer method allows a continuous tuning of the coupling strength (see supplementary video). Between no coupling at the field minimum

and the maximal strong coupling at the field maximum should be a coupling strength referring to weak coupling prior to reaching the EP. Thus, weak coupling could be realized by placing the

monolayer near the field minimum combined with the given tuning mechanism. CONCLUSION In summary, we have presented two designs for an open planar FP microcavity system, which both allow

nearly material independent, active and continuous modification of the light–matter interaction in the structure according to calculations. Hence, such setups can be especially utilized as a

testbed for real-time investigations on the transition between the strong and weak coupling regime. Beyond the employment of 2D-cavity systems for optoelectronic coupling, the alternative

free-standing-sheet configuration could even enable sophisticated optomechanical experiments. The more practical variant utilizing a spacer layer on one of the DBRs of the FP cavity, as an

alternative concept to a displaceable free-standing sheet medium, is characterized theoretically in detail with a transfer-matrix model for a tuneable variation of the coupling strength. The

choice of the spacer layer’s thickness allows a precise control of the coupling situation. Thereby, an increase and decrease in the obtainable Rabi splitting as well as a modification of

the coupling regime become possible scenarios while spectral resonance between cavity and exciton is realized. A setup of this kind is suitable for material systems with a sub-wavelength 

thickness with respect to their exciton emission wavelength, provided that a large enough oscillator strength for strong coupling is exhibited. As such, also an extension to the ultra-strong

coupling regime46,47 should be possible; here, molecular materials could be a good choice, as they offer very large dipole moments at comparably low film thicknesses48,49,50. In the future,

this method could be used to investigate light–matter coupling not only for 2D semiconductors, but also e.g. quantum dots, perovskite thin films, nanoplatelets or molecular films.

REFERENCES * Yamamoto, Y. & Imamoglu A. _Mesoscopic Quantum Optics_. (John Wiley & Sons, 1999). * Vahala, K. _Optical microcavities_. (World Scientific, 2007). * Kavokin, A. V.,

Baumberg, J. J., Malpuech, G. & Laussy, F. P. _Microcavities_. (ed. 2nd) (Oxford University Press, 2017). * Purcell, E. Spontaneous emission probabilities at radio frequencies. _Phys.

Rev._ 69(11–12), 674–674 (1946). Google Scholar  * Weisbuch, C., Nishioka, M., Ishikawa, A. & Arakawa, Y. Observation of the coupled exciton-photon mode splitting in a semiconductor

quantum microcavity. _Phys. Rev. Lett._ 69, 3314 (1992). Article  ADS  CAS  PubMed  Google Scholar  * Deng, H., Haug, H. & Yamamoto, Y. Exciton-polariton Bose-Einstein condensation.

_Rev. Mod. Phys._ 82, 1489 (2010). Article  ADS  CAS  Google Scholar  * Yamamoto, Y., Tassone, F. & Cao, H. _Semiconductor Cavity Quantum Electrodynamics_. (Springer-Verlag, 2000). *

Vahala, K. Optical microcavities. _Nature_ 424, 839 (2003). Article  ADS  CAS  PubMed  Google Scholar  * Reitzenstein, S. & Forchel, A. Quantum dot micropillars. _J. Phys. D: Appl.

Phys._ 43, 033001 (2010). Article  ADS  CAS  Google Scholar  * Sanvitto, D. & Kéna-Cohen, S. The road towards polaritonic devices. _Nat. Mater._ 15, 1061 (2016). Article  ADS  CAS 

PubMed  Google Scholar  * Deng, H., Weihs, G., Santori, C., Bloch, J. & Yamamoto, Y. Condensation of semiconductor microcavity exciton polaritons. _Science_ 298, 199 (2002). Article  ADS

  CAS  PubMed  Google Scholar  * Kasprzak, J. _et al_. Bose–Einstein condensation of exciton polaritons. _Nature_ 443, 409–414 (2006). Article  ADS  CAS  PubMed  Google Scholar  * Schneider,

C. _et al_. An electrically pumped polariton laser. _Nature_ 497, 348–352 (2013). Article  ADS  CAS  PubMed  Google Scholar  * Bhattacharya, P. _et al_. Solid State Electrically Injected

Exciton-Polariton Laser. _Phys. Rev. Lett._ 110, 206403 (2013). Article  ADS  PubMed  CAS  Google Scholar  * Plumhof, J. D., Stoeferle, T., Mai, L., Scherf, U. & Mahrt, R. Room

temperature Bose–Einstein condensation of cavity exciton–polaritons in a polymer. _Nat. Mater._ 13, 328–329 (2014). Article  CAS  Google Scholar  * Daskalakis, K. S., a Maier, S., Murray, R.

& Kéna-Cohen, S. Nonlinear interactions in an organic polariton condensate. _Nat. Mater._ 13, 271–8 (2014). Article  ADS  CAS  PubMed  Google Scholar  * Christopoulos, S. _et al_.

Room-Temperature Polariton Lasing in Semiconductor Microcavities. _Phys. Rev. Lett._ 98, 126405 (2007). Article  ADS  CAS  PubMed  Google Scholar  * Bhattacharya, P. _et al_. Room

Temperature Electrically Injected Polariton Laser. _Phys. Rev. Lett._ 112, 236802 (2014). Article  ADS  PubMed  CAS  Google Scholar  * Liu, X. _et al_. Strong light–matter coupling in

two-dimensional atomic crystals. _Nat. Phot._ 9, 30–34, https://doi.org/10.1038/nphoton.2014.304 (2014). Article  CAS  Google Scholar  * Flatten, L. C. _et al_. Room-temperature

exciton-polaritons with two-dimensional WS2. _Scientific reports_ 6, 33134 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Wang, S. _et al_. Coherent Coupling of WS2

Monolayers with Metallic Photonic Nanostructures at Room Temperature. _Nano Lett._ 16, 4368 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Lundt, N. _et al_. Observation of macroscopic

valley-polarized monolayer exciton-polaritons at room temperature. _Phys. Rev. B_ 96, 241403 (2017). Article  ADS  Google Scholar  * Sun, Z. _et al_. Optical control of room-temperature

valley polaritons. _Nat. Phot._ 11, 491–496 (2017). Article  CAS  Google Scholar  * Zhang, L., Gogna, R., Burg, W., Tutuc, E. & Deng, H. Photonic-crystal exciton-polaritons in monolayer

semiconductors. _Nat. Comm._ 9, 713 (2018). Article  ADS  CAS  Google Scholar  * Hertzog, M., Wang, M., Mony, J. & Börjesson, K. Strong light-matter interactions. A new direction within

chemistry. _Chem. Soc. Rev._ 48, 937–961 (2019). Article  CAS  PubMed  PubMed Central  Google Scholar  * Wang, G. _et al_. In-Plane Propagation of Light in Transition Metal Dichalcogenide

Monolayers: Optical Selection Rules. _Phys. Rev. Lett._ 119, 047401 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Glazov, M. M. _et al_. Exciton fine structure and spin decoherence in

monolayers of transition metal dichalcogenides. _Phys. Rev. B_ 89, 201302 (2014). Article  ADS  CAS  Google Scholar  * Rodriguez, S. R.-K. Classical and quantum distinctions between weak

and strong coupling. _Eur. J. Phys._ 37, 25802 (2016). Article  Google Scholar  * Novotny, L. Strong coupling, energy splitting, and level crossings: A classical perspective. _Am. Jour. of

Phys._ 78, 1199 (2010). Article  ADS  Google Scholar  * El-Ganainy, R. _et al_. Non-Hermitian physics and PT symmetry. _Nat. Phys._ 14, 11 (2018). Article  CAS  Google Scholar  * Heiss, W.

D. The physics of exceptional points. _J. Phys. A: Math. Theor._ 45, 444016 (2012). Article  ADS  MathSciNet  MATH  Google Scholar  * Peng, B. _et al_. Chiral modes and directional lasing at

exceptional points. _PNAS_ 113, 6845 (2016). Article  ADS  CAS  PubMed  PubMed Central  Google Scholar  * Xu, H., Mason, D., Jiang, L. & Harris, J. G. E. Topological energy transfer in

an optomechanical system with exceptional points. _Nature_ 537, 80 (2016). Article  ADS  CAS  PubMed  Google Scholar  * Chen, W. _et al_. Exceptional points enhance sensing in an optical

microcavity. _Nature_ 548, 192 (2017). Article  ADS  CAS  PubMed  Google Scholar  * Chakraborty, B. _et al_. Control of Strong Light–Matter Interaction in Monolayer WS2 through Electric

Field Gating. _Nano Lett._ 18, 6455 (2018). Article  ADS  CAS  PubMed  Google Scholar  * Liu, X. _et al_. Control of Coherently Coupled Exciton Polaritons in Monolayer Tungsten Disulphide.

_Phys. Rev. Lett._ 119, 27403 (2017). Article  ADS  Google Scholar  * Schwartz, T., Hutchison, J. A., Genet, C. & Ebbesen, T. W. Reversible Switching of Ultrastrong Light-Molecule

Coupling. _Phys. Rev. Lett._ 106, 196405 (2011). Article  ADS  CAS  PubMed  Google Scholar  * Wang, S. _et al_. Quantum Yield of Polariton Emission from Hybrid Light-Matter States. _J. Phys.

Chem. Lett._ 5, 1433–1439 (2014). Article  CAS  PubMed  Google Scholar  * Gao, W., Li, X., Bamba, M. & Kono, J. Continuous transition between weak and ultrastrong coupling through

exceptional points in carbon nanotube microcavity exciton–polaritons. _Nat. Phot._ 12, 362–367 (2018). Article  CAS  Google Scholar  * Malitson, I. H. Interspecimen Comparison of the

Refractive Index of Fused Silica. _J. Opt. Soc. Am._ 55, 1205 (1965). Article  ADS  CAS  Google Scholar  * Luke, K. _et al_. Broadband mid-infrared frequency comb generation in a Si3N4

microresonator. _Opt. Lett._ 40, 4823 (2015). Article  ADS  CAS  PubMed  Google Scholar  * Li, Y. _et al_. Measurement of the optical dielectric function of monolayer transition-metal

dichalcogenides: MoS2, MoSe2, WS2, and WSe2. _Phys. Rev. B_ 90, 205422 (2014). Article  ADS  CAS  Google Scholar  * Weismann, M. & Panoiu, N. C. Theoretical and computational analysis of

second- and third-harmonic generation in periodically patterned graphene and transition-metal dichalcogenide monolayers. _Phys. Rev. B_ 94 (2016). * Girault, P. _et al_. Integrated polymer

mirco-ring resonators for optical sensing applications. _J. App. Phys._ 117, 104504 (2015). Article  ADS  CAS  Google Scholar  * Sultanova, N., Kasarova, S. & Nikolov, L. Dispersion

Properties of Optical Polymers. _Acta Phys. Pol. A_ 116, 585 (2009). Article  ADS  CAS  Google Scholar  * Kockum, A. F., Miranowicz, A., De Liberato, A., Savasta, S. & Nori, F.

Ultrastrong coupling between light and matter. _Nat. Rev. Phys._ 1, 19–40 (2019). Article  Google Scholar  * Forn-Diaz, P., Lamata, L., Rico, E., Kono, J. & Solano, E. Ultrastrong

coupling regimes of light-matter interaction. _Rev. Mod. Phys._ 91, 025005 (2019). Article  ADS  CAS  Google Scholar  * Barachati, F. _et al_. Tunable Third-Harmonic Generation from

Polaritons in the Ultrastrong Coupling Regime. _ACS Photonics_ 5, 119–125 (2018). Article  CAS  Google Scholar  * Eizner, E., Brodeur, J., Barachati, F., Sridharan, A. & Kéna-Cohen, S.

Organic Photodiodes with an Extended Responsivity Using Ultrastrong Light-Matter Coupling. _ACS Photonics_ 5, 2921–2927 (2018). Article  CAS  Google Scholar  * Genco, A. _et al_. Bright

Polariton Coumarin-Based OLEDs Operating in the Ultrastrong Coupling Regime. _Adv. Opt. Mater._ 6, 1–6 (2018). Article  CAS  Google Scholar  Download references ACKNOWLEDGEMENTS The authors

acknowledge financial support by the German Research Foundation (DFG: SFB1083, RA2841/5-1), by the Philipps-Universität Marburg, by the Federal Ministry of Education and Research (BMBF) in

the frame of the German Academic Exchange Service’s (DAAD) program Strategic Partnerships and Thematic Networks. The authors thank Fang Wei from the Zhejiang University, China, for useful

discussions. AUTHOR INFORMATION AUTHORS AND AFFILIATIONS * Faculty of Physics and Materials Sciences Center, Philipps-Universität Marburg, D-35032, Marburg, Germany Franziska Wall, Oliver

Mey, Lorenz Maximilian Schneider & Arash Rahimi-Iman Authors * Franziska Wall View author publications You can also search for this author inPubMed Google Scholar * Oliver Mey View

author publications You can also search for this author inPubMed Google Scholar * Lorenz Maximilian Schneider View author publications You can also search for this author inPubMed Google

Scholar * Arash Rahimi-Iman View author publications You can also search for this author inPubMed Google Scholar CONTRIBUTIONS A.R.-I. initiated the light–matter coupling considerations with

tunable open microcavities and guided the work. F.W. contributed the spacing-layer idea, the implementation of the TMM software and performed the simulations. O.M. was involved in the

development of the spacing-layer idea, the TMM calculation tool as well as the visualization. L.M.S. supported the overall research. The manuscript was written by all authors. CORRESPONDING

AUTHOR Correspondence to Arash Rahimi-Iman. ETHICS DECLARATIONS COMPETING INTERESTS The authors declare no competing interests. ADDITIONAL INFORMATION PUBLISHER’S NOTE Springer Nature

remains neutral with regard to jurisdictional claims in published maps and institutional affiliations. SUPPLEMENTARY INFORMATION SUPPLEMENTARY INFORMATION. SUPPLEMENTARY VIDEO RIGHTS AND

PERMISSIONS OPEN ACCESS This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any

medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The

images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not

included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly

from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/. Reprints and permissions ABOUT THIS ARTICLE CITE THIS ARTICLE Wall, F., Mey, O.,

Schneider, L.M. _et al._ Continuously-tunable light–matter coupling in optical microcavities with 2D semiconductors. _Sci Rep_ 10, 8303 (2020). https://doi.org/10.1038/s41598-020-64909-1

Download citation * Received: 04 November 2019 * Accepted: 26 December 2019 * Published: 19 May 2020 * DOI: https://doi.org/10.1038/s41598-020-64909-1 SHARE THIS ARTICLE Anyone you share the

following link with will be able to read this content: Get shareable link Sorry, a shareable link is not currently available for this article. Copy to clipboard Provided by the Springer

Nature SharedIt content-sharing initiative